基于改进遗传算法的带时间窗城市配送路径多目标优化

田帅辉 欧丽英

摘  要：城市居民小批量、个性化、便利化、高效化等配送需求以及日益拥堵的城市交通对城市配送效率提出更高的挑战。针对城市配送路径优化问题，以平均配送时间与总配送费用帕累托最优为目标，构建考虑时间窗的城市配送车辆路径优化模型，对遗传算法进行改进，在标准遗传算法的基础上加入筛选算子和择优算子并适当改进初始种群设计和选择、交叉算子，最后通过算例验证模型的可行性和改进算法的有效性。结果表明改进后的遗传算法在求解考虑时间窗的车辆路径优化模型时，相较于标准的遗传算法的寻优能力有显著优势。

关键词：改进遗传算法;时间窗;多目标优化;城市配送

中图分类号：F272.14    文献标识码：A

Abstract： The distribution needs of urban residents， such as small batch， individualization， convenience， high efficiency and increasingly congested urban traffic， pose a higher challenge to the efficiency of urban distribution. Aiming at the problem of urban distribution routing optimization， taking the Pareto optimization of average distribution time and total distribution cost as the objective， a vehicle routing optimization model with time windows for urban distribution considering time window is construct， and the genetic algorithm is also improved， which is added screening operator and optimizing operator on the basis of standard genetic algorithm， and the initial population design and selection， crossover operator is improved appropriately. Finally， the feasibility of the model and the effectiveness of the improved algorithm are verified by an example. The results show that the improved genetic algorithm has significant advantages over the standard genetic algorithm in solving the vehicle routing optimization model with time windows.

Key words： improved genetic algorithm; time window; multi-objective; urban distribution

0  引  言

近年來，随着电子商务、O2O、新零售等新型商业模式的迅猛发展，全国城市配送市场规模已突破万亿，预计2021年将超过2万亿。同时，我国城市居民的消费需求呈现小批量、个性化、多样化、便利化、高效化等特征，这对城市配送效率提出了更高的要求和挑战。

围绕城市配送路径优化，国内外学者进行了深入的研究。关于城市配送路径优化，部分学者从优化算法的角度进行研究。其中，吴聪[1]令遗传算法交叉系数和变异系数随适应度的大小、迭代次数和进化过程中个体未改变的数目自适应调整;罗勇[2]提出对遗传算法算子进行改进;申艳光[4]、胡钟骏[5]等则将遗传算法与其他算法进行结合，结合其他算法的优势来弥补遗传算法的不足。同时由于车辆路径问题（Vehicle Routing Problem， VRP）在现实情况下会受到多方面因素的影响，部分学者在考虑该问题时从多目标进行优化[6-8]。随着顾客对配送时效的要求日益提高，时间成为影响消费者满意度的一个至关重要的因素，国内外研究学者也纷纷将时间作为重要目标之一运用蚁群算法[9]、粒子群算法[10-11]、遗传算法和一些混合算法等进行路径优化;就遗传算法而言，侯玉梅[12]、Tas[13]等强调软时间窗对物流配送优化所起到的关键作用。这些研究强调了不同算法下的时间限定，从以上分析可以发现，目前大多数研究运用遗传算法进行配送路径优化侧重于结合其他算法的优势，而从多目标优化出发，强调时间窗和载重约束，通过添加新的遗传算法算子进行改进相对较少。因此本文结合实际情景，在强调时间和成本两个目标在城市配送路径优化的重要性上对遗传算法进行优化，受人工培育豌豆的启发优化寻优过程，结合实际条件约束，改进相应的算法步骤并添加相关的算子，在充分利用遗传算法全局搜索特性的同时，使其在解决有时间窗车辆路径问题（Vehicle Routing Problems with Time Windows，VRPTW）问题时寻优能力更佳，得到更有效可靠的解。通过和标准遗传算法的寻优结果进行对比，验证改进后的遗传算法具有更强的寻优能力。

1  模型构建

1.1  问题描述及符号说明

带软时间窗的多目标城市配送车辆路径优化问题（多目标VRPTW）描述为（如图1所示）：某城市配送中心拥有Kk∈K辆型号规格完全一样的配送车辆，其最大载重量G完全相同，且城市配送中心货物充足。现有Mi，j∈M个客户需要服务，i，j=0时表示城市配送中心，且客户i的需求量g、客户规定的时间窗et，lt、城市配送中心与各顾客之间距离d（直线距离）均已知。配送车辆未在时间窗内送达将受到相应的惩罚，惩罚成本与该客户的配送费用成正相关。通过合理的调度方案使得城市配送车辆平均配送时间和配送成本达到帕累托最优。

成本：H為车辆k的固定使用成本;f为每升油的燃烧成本（L/元）;p为向客户收取的货物单位重量运费（t/千元）;C为总配送车辆的固定成本;C为总运输费用，其跟运输距离有关;C为总超出时间窗惩罚成本;C为总配送成本;C为最大预计消耗的配送成本。

时间：t为配送车辆k到达客户i的时间，t为配送车辆k从城市配送中心出发的时间;u为单位货物卸货所需时间

（t/h）;t为车辆k从客户i到客户j所用时间;T为完成本次配送任务配送车辆平均所用时间;T为每辆配送车平均最大预计消耗的配送时间。

车辆载重及油耗：g为车辆k从客户i到客户j配送中的载货重量;O为车辆k从客户i到客户j配送中的单位距离耗油量（km/L），与车辆当前承载重量有关;O为车辆空载时的单位距离耗油量;O为车辆满载时车辆自重和最大承载重量的单位距离耗油量。

权重：u为提前到达的时间惩罚权重;u为延后到达的时间惩罚权重;u为时间系数，配送中心可根据顾客对时间的重视程度分配相应的权重;u为成本系数，配送中心可根据顾客对成本的重视程度分配相应的权重。

决策变量：x表示车辆k是否从客户i到客户j，如果是，则为1，否为0;y表示车辆k是否到客户i，如果是，则为1，否为0。

1.2  基本假设

考虑到现实情况，针对城市配送车辆配送环境做出如下假设：

（1）只有一个城市配送中心，城市配送中心不会出现缺货;

（2）所有客户所需的商品均由城市配送中心供给，客户之间不存在相互调配的情况;

（3）配送车辆的起点和终点均为城市配送中心;

（4）车辆在配送时路况稳定，不会出现拥堵情况，车辆匀速行驶，行驶速度为v;

（5）各客户的需求量确定并且保持稳定不会变动;

（6）一辆车可以配送多个客户，但一个客户只能由一辆车提供服务，顾客的需求必须满足;

（7）单位距离油费与车辆当前载重呈线性关系。

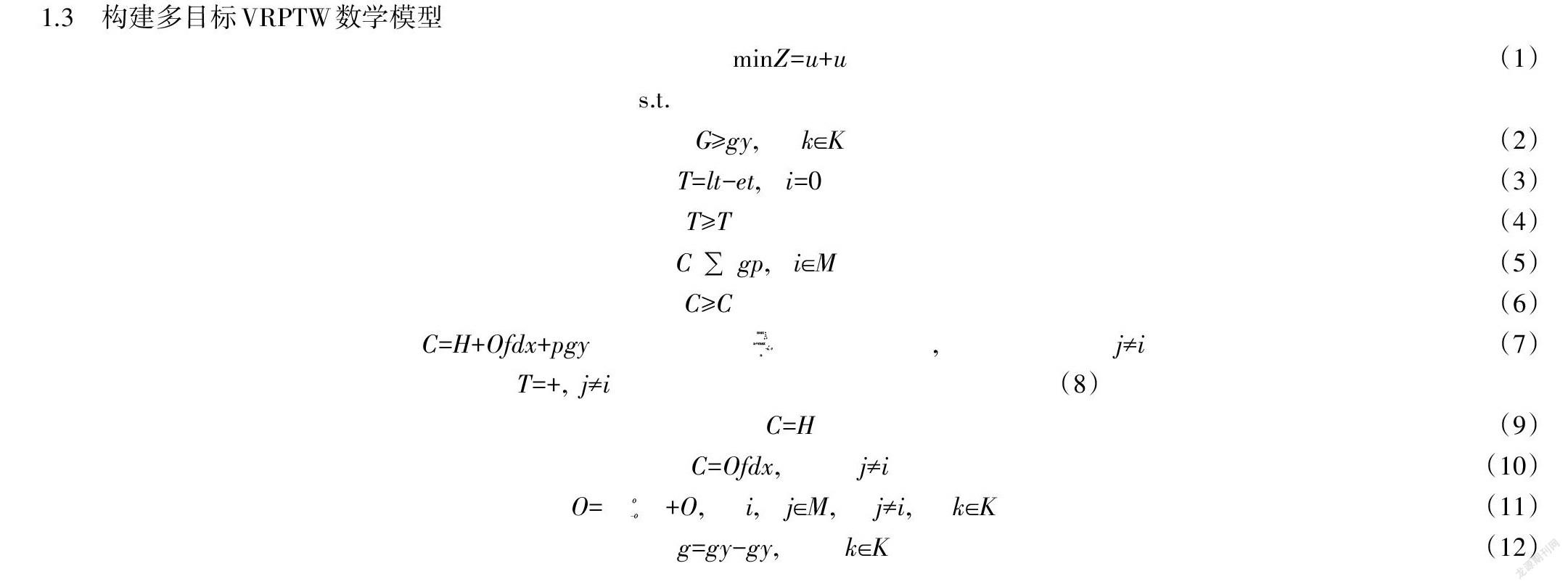
1.3  构建多目标VRPTW数学模型

minZ=u+u                                          （1）

s.t.

G≥gy， k∈K                                             （2）

T=lt-et， i=0                                                （3）

T≥T                                                      （4）

C∑gp， i∈M                                               （5）

C≥C                                                      （6）

C=H+Ofdx+pgymaxet-t-ug， 0u+maxt-lt， 0u， j≠i             （7）

T=+， j≠i                                （8）

C=H                                               （9）

C=Ofdx， j≠i                                      （10）

O=O-O+O， i，j∈M， j≠i， k∈K                                 （11）

g=gy-gy， k∈K                                       （12）

C=pgymaxet-t-ug， 0u+maxt-lt， 0u                          （13）

t=maxet， t+ugy+xt， j∈M， i≠j， k∈K                             （14）

t≤lt， i=0， k∈K                                          （15）

t=， i，j∈M， j≠i                                         （16）

x=1， j∈M， j≠i                                       （17）

y=1， j∈M， j≠0                                         （18）

x=x， j=0， k∈K                                       （19）

式（1）表示總目标函数，为城市配送车辆平均配送时间和配送总成本在无量纲化后加权之和最小;式（2）表示每次配送中心给车辆安排的配送货物重量不能超过车辆的最大载重量;式（3）表示平均最大预计消耗的配送时间由城市配送中心提供服务的时间区间决定;式（4）表示实际消耗的平均配送时间不能大于平均最大预计消耗的配送时间;式（5）表示最大预计消耗的配送费用等于配送所获得的收入;式（6）表示实际消耗的配送总成本不能大于配送所获得的收入;式（7）表示配送总成本，由总配送车辆固定使用费用、总运输费用、总超出时间窗惩罚费用组成;式（8）表示平均配送时间;式（9）表示总配送车辆固定使用费用，包括所有使用车辆及其配送货物的保险费用、车辆的维护、司机的工资、路桥费等;式（10）表示总运输费用及完成所有配送任务后，配送车辆所产生的燃油费;式（11）表示配送车辆的单位距离耗油量，与车辆当前载货重量成正相关;式（12）表示配送车辆当前载货重量，及该配送车辆从配送中心出发时的载货重量减去已经完成配送的客户需求总和;式（13）表示总超出时间窗惩罚费用，在车辆配送过程中，如果提前到达客户点可先进行卸货再计算等待时间，且不考虑“配送车辆到达客户点未超出客户时间窗，但加上卸货时间超过客户时间窗，因而索赔客户超出时间窗的卸货时间的惩罚费用”的情况;式（14）表示配送车辆到达客户点的时间，配送车辆只能在客户时间窗内进行交付行为，即如果配送车辆到达客户点并完成卸货，依旧未达到客户起始服务时间，必须等到客户起始服务时间后才能前往下一个客户点;式（15）表示配送车辆完成配送任务返回城市配送中心的时间不能大于城市配送中心提供服务的终点时刻;式（16）表示配送车辆从一个客户点到另一个客户点匀速行驶所耗时间;式（17）每一位客户都需要被服务;式（18）表示一位客户只由一辆配送车提供服务;式（19）表示配送车辆从配送中心发出，完成配送任务后返回配送中心。

2  算法设计

2.1  遗传算法改进思路

本文基于标准遗传算法，通过模仿人工培育豌豆的过程，对遗传算法进行一定改进，基本思路如下：

步骤1：在初始种群设计和适应度计算间和变异完成后加入筛选环节，及将含需求基因的豌豆挑选出来进行培育;

步骤2：在适应度计算和选择之间加入择优环节，将优秀的个体进行自花授粉，将次优的个体异花传粉，将劣势的个体淘汰;

步骤3：让初始种群数作为环境最大容纳量，这样更容易观察种群平均适应度的变化情况;

步骤4：适当地改进了初始种群设计和选择、交叉算子使其更加符合实际情况。

2.2  改进的遗传算法实现步骤

（1）编码方式。本文采用十进制编码方式，城市配送中心使用k辆大小型号一致的配送车辆为N个客户配送货物。其中配送中心用0表示，客户点用1，2，3，…，N表示。由于配送车辆是同一时间为每个客户配送货物且一次完成，所以配送车辆数量决定配送子路径的数量，因此一条染色体的长度为K+N+1，例如一条染色体的编码为“0 5 6 0 10 8 4 0 2 1 9 7 0 3 0”，表示4辆配送车辆同时为10个客户点配送货物，配送子路径：

0→5→6→0，0→10→8→4→0，0→2→1→9→7→0，0→3→0

（2）初始种群设计。产生初始种群数POP *客户数M的矩阵，矩阵的每一行都是1到M的随机不重复的数字，其中POP也是该种群的环境最大容纳量。计算每一辆车的预计承重量G， G≤G， G=∑g/K/Φ2， Φ2=0.9544，再将客户点的矩阵转换为客户点需求矩阵，然后在矩阵的每一行中从左到右累加得到S， x∈M， S=0，x表示列数，S表示0到x列客户需求量之和。当时，S=S-S，并在x列和x+1列间插0。

（3）种群筛选算子。对插0后的矩阵，进行每一条染色体中每一辆车货物载重量Gk∈K的统计，其中G=S，一旦一条染色体中出现货物载重量大于车辆最大承重量时，及G？酆G时，删除该染色体。

（4）适应度计算。在遗传算法中，适应度的高低决定了种群中个体性能的优劣，一般情况下，适应度越大的个体其性能越优秀。本文将目标函数Z的倒数作为适应度，及第y行染色体的适应度f=， y∈YS，YS表示经过种群筛选后的染色体的数量。

（5）择优算子。通过模拟人工培养豌豆授粉的过程，将优秀的个体进行自花授粉，将次优的个体异花传粉，将劣势的个体淘汰。将已经按适应度从大到小的顺序排列好的矩阵，选出排在矩阵前面5%的染色体作为自交个体，将剩余的染色体进入选择阶段。自交个体自交生成2倍于自身数量的个体，直接进入变异阶段。生成2倍于自身数量的个体是为了减少变异对优秀基因的损坏，尽可能的保护优秀基因。

（6）选择算子。轮盘赌法是一个十分实用的选择方法，但这种方法存在选择概率高的个体被多次选出的情况，这可能较大的削减了种群的规模，降低了种群的多样性，陷入局部最优的可能性较大。因此本文将在轮盘赌法的基础上进行改进，即第y条染色体被选出进入交叉阶段的概率为：

P=， y∈YX                                      （20）

YX表示进入选择阶段染色体的数量，ci表示当前染色体被重复选中的总次数，例如：在第y条染色体前，只有第r条染色体被选中2次和第q条染色体被选中3次，此时ci=3; r，q∈YX。然后生成一个0到1的随机数？鄣，当P？刍？鄣≤P时，染色体y被选中。此时染色体再次被选中的概率为：

P=P-， P≥0，当P？刍0时，P=0                          （21）

其中：等式右边的P表示染色体y前一次被选中的概率，f表示所有进入选择阶段中的染色体最大的适应度，表示所有进入选择阶段中的染色体平均适应度。然后执行H次轮盘操作，并将其中重复的染色体除去重复部分。

H=YX/P， P=1-                                   （22）

其中：P表示适应度最大值到平均适应度的染色体数量占进入交叉阶段染色体数量的比例。

（7）交叉算子。由于种群筛选步骤的筛选力度较大，一旦染色体出现超载情况，就会被删除，所以采用一种尽量避免超载的交叉方案。步骤如下：

步骤1：将符合交叉概率p的随机父代1和父代2中，从父代1随机选出一辆车的行驶路径作为交叉片段（不包括0）;

步骤2：找出父代2中对应父代1交叉片段的编号顺序，作为父代2的交叉片段;

步骤3：将父代1的交叉片段与父代2的交叉片段进行互换，生成子代1和子代2;

步骤4：重复步骤1到3，直到生成YB条染色体停止交叉，YB=P-2*5%*YS， P表示环境最大容纳量，YS表示经过种群筛选后的染色体的数量。交叉操作、交叉结果具体过程图3所示。

（8）变异算子。在染色体满足变异概率p时，从2，N+K中随机选出两个不相同且不为0的数字，将数字对应的染色体基因码进行互换，生成新的染色体。变异具体过程图4所示。

（9）种群筛选算子。将完成变异的矩阵转换为客户点需求矩阵，在对每一条染色体的每一辆车货物载重量Gk=1，2，3，…，K进行统计，一旦一条染色体中出现货物载重量大于车辆最大承重量时，即G？酆G时，删除该染色体。

3  实验结果与分析

3.1  实验数据

一个城市配送中心为20个客户提供配送服务，配送车辆最大载重为2t，车辆配送行驶平均速度为40km/h，车辆固定租赁费用为500元，油费为7元/L，每吨货物卸货时间为0.001kg/h，重量的运费为1元/kg，车辆空载时耗油量为1L/km，车辆满载时耗油量为2L/km，超出时间窗惩罚系数为0.3，提前时间窗惩罚系数为0.1。配送中心和客戶点的坐标、客户需求量、服务客户的时间窗如表1所示。

改进遗传算法参数设定：种群规模为1 000，迭代次数为1 000，择优概率为0.05，变异概率为0.1。

3.2  实验结果

本实验采用MATLAB R2015（b）实现，在Intel（R）Core（TM）i5-6 200U CPU 2.4GHz，内存8G的电脑上重复运行多次。种群内个体适应度整体进化过程如图5所示，由适应度最大值进化曲线发现种群最佳适应度在150代之前增长迅速，在200代左右趋近于稳定。由适应度平均进化曲线发现在150代内适应度平均值稳步上升并在250代后趋近于稳定并略低于适应度最大值。随着种群的迭代总成本和总时间的变化曲线如图6所示。

如图7和图8所示，使用改进遗传算法和标准遗传算法同时解决上述问题时。改进后的遗传算法收敛速度明显增快并且能优化整个种群平均适应度以避免局部最优;相比标准遗传算法在解决上述问题时则容易陷入局部最优导致不能得到最优解。

图9和图10分別表示改进遗传算法和标准遗传算法解决上述问题时的最优车辆路径。

表2和表3分别表示标准遗传算法和改进遗传算法解决上述问题的最终数据结果，分析表明标准遗传算法在解决多目标问题上不能同时兼顾路径长度、时间和惩罚成本，在数据方面有比较大的波动。改进后的遗传算法对路径长度、时间和惩罚成本同时进行优化，数据趋于稳定。

通过对标准遗传算法和改进遗传算法相比，如表4所示。可以发现，改进遗传算法在解决算例中20位客户配送问题时要比标准遗传算法具有更强的寻优能力，可以达到同时对行驶距离、时间和成本优化的目的。

计算结果分析表明相比标准遗传算法，改进后的遗传算法在车辆行驶距离节约14.2%，时间节约6%，成本节约6.3%，总利润增加7.9%。综上所述，改进后的遗传算法在解决城市配送多目标优化问题上有一定的优势。

4  结束语

本文针对城市配送问题，通过建立多目标VRPTW模型，考虑车辆载重限制，对时间、成本这两个目标同时进行优化求解。针对标准遗传算法在解决大规模VRPTW问题时容易陷入局部最优，通过加入种群筛选和择优两个算子加大了遗传算法的寻优力度;改进的选择算子在选择出优秀个体的同时，也保证了父代规模;改进交叉方式在尽量避免超载的同时，又保证了种群多样性避免出现局部最优。最后通过对比实验结果验证改进后的遗传算法具有更强的寻优能力，可以有效地解决大规模VRPTW问题。但本文未考虑“双11”、“618”等重要电商节日时出现客户数量和配送量剧增的现实情况，后续的研究中会加以改进。

参考文献：

[1] 吴聪，陈侃松，姚静. 基于改进自适应遗传算法的物流配送路径优化研究[J]. 计算机测量与控制，2018，26（2）：236-240.

[2] 罗勇，陈治亚. 基于改进遗传算法的物流配送路径优化[J]. 系统工程，2012，30（8）：118-122.

[3]  Esam T Y， Masri A， et al. An Adaptive Hybrid Algorithm for Vehicle Routing Problems with Time Windows[J]. Computers and Industrial Engineering， 2017（113）：382-391.

[4] 申艳光，张玲玉，刘永红. 基于混合遗传算法的物流路径优化方法研究[J]. 计算机技术与发展，2018，28（3）：192-196.

[5] 胡钟骏，周泓. 改进遗传算法的需求可拆分车辆路径优化研究[J]. 计算机仿真，2018，25（3）：80-83.

[6] 金仙力，李金刚. 基于遗传算法的多目标路径优化算法的研究[J]. 计算机技术与发展，2018，28（2）：54-58.

[7] 葛显龙，谭柏川，吴宁谦. 基于碳交易机制的带时间窗车辆路径问题与算法研究[J]. 管理工程学报，2018，32（4）：141-148.

[8]  Ahmed F， Deb K. Multi-objective Optimal Path Planning Using Elitist Non-dominated Sorting Genetic Algorithms[J]. Soft Computing， 2013，17（SI）：1283-1299.

[9] 曹倩，邵举平，孙延安. 基于改进遗传算法的生鲜农产品多目标配送路径优化[J]. 工业工程，2015，18（1）：71-76.

[10] 刘澜，吴金卓，胡鸿. 交通限制和软时间窗条件下的车辆路径问题及其蚁群算法改进[J]. 物流科技，2016，35（9）：92-96.

[11] 周蓉，沈维蕾，刘明周，等. 带时间窗装卸一体化车辆路径问题的混合离散粒子群优化算法[J]. 中国机械工程，2016，27（4）：495-502.

[12] 侯玉梅，贾震环，田歆，等. 带软时间窗整车物流配送路径优化研究[J]. 系统工程学报，2015，30（2）：240-249.

[13]  DUYGU T， OLA J， TOM V W. A Vehicle Routing Problem with Flexible Time Windows[J]. Computers and Operations Research， 2014，52：39-54.