以探究圆的特点为例谈对解决问题能力的培养

江苏省如皋市港城实验学校 吴海虹

小学阶段的学生由于年龄较小，还处在对事物抱有好奇心、爱玩好动的年龄阶段，沉下心来积极探索知识对他们而言是较为困难的一件事情。因此，教师在引导学生探讨“是否只有圆才能在地上平稳滚动”这一问题时，应当有效地将知识与生活实际中的事物相结合，加深学生对于圆的知识以及特性的认识。

一、问题导入，通过疑问激发学生提出问题的能力

教师在进行知识教学的时候，应当以多样化的教学模式有效激发学生对于圆这一知识的学习兴趣，让学生能积极参与到课堂活动中，提高学生的参与度。教师可以通过提出疑问、解决疑问的教学模式进行课程导入。例如，教师在上课之前直接询问学生：“同学们知道现实生活中有哪些物品是圆形的吗？圆有什么特性呢？”学生可能会说瓶盖、球面、乒乓球拍的拍面等等，但是他们可能无法准确讲出圆的概念，也无法说出圆有哪些特性，往往只能说出“圆能在地面上滚动”。教师用提出疑问的方式引出下一个话题：“圆的确能在地面上滚动，但是这真的能够算作圆的独有特性吗？那有没有其他的图形也能够在地面上平稳滚动呢？”提出疑问的方式能有效锻炼学生探究问题的能力，同样也能有效地开发学生的思维，让学生能对数学知识抱有好奇心。

二、抓住特点，通过操作提高学生的解决能力

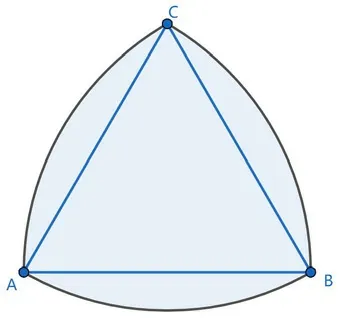
在地面上能够平稳滚动的不仅仅只有圆，还有其他的封闭图形。教师在教学相关知识的时候，首先要为学生介绍相关概念解释，只有学生真正掌握概念，才能更加深入地利用知识解决疑难问题。概念理解是认识的过程，解决疑难问题是实践的过程，实践是认识的检验标准，概念的分析在解决问题的过程中得到深化和探究。在讨论总结“图形为什么能够在平地上平稳滚动”时，应当对图形的形状特点进行分析，只有找准切入点，才能真正解决问题。图形之所以能在平地上平稳滚动，是其有“定宽性”这一特点。定宽性主要指的是用两条平行直线去夹住这个图形，不论这个图形怎样移动，两条平行线之间的距离不变，而这两条平行线之间的距离则为封闭图形的宽。教师可以根据这一特性引导学生绘出图形，若想要在滚动过程中宽不变，则应当从等边三角形入手，等边三角形的三条边相等，若是将三角形的三个顶点之间以等边三角形的边长为半径画圆，将三个顶点连接起来，那么不论这个封闭的图形如何运动，其宽都是等边三角形的边长，则这个图形具有定宽性。教师在引导学生绘制出这个图形之后，让他们剪切下来并进行实验，看其是否能在平地上平稳滚动。教学的目的不仅在于教学知识，同样还在于教学解决问题的思维模式以及切入点，只有这样，才能够在根本上提高学生的数学能力。

三、总结方法，巩固学生解决问题的思维方式

教师在引导学生对圆的特性进行探索的同时，应当让他们了解教师的思维模式，在解决问题的过程当中明白解决问题的思路，潜移默化地培养探索知识的意识。解决问题之前，要理解问题、分析问题，找到问题真正的出题点。因此，在面对“是否只有圆才能在平地上平稳滚动”这一问题时，教师应当肯定学生的质疑精神，让学生从否定的角度、批评的角度去看待这一问题，寻找问题的突破口，而突破口则在于对于圆特性的研究。教师在教学知识的同时，应当注重学生思维模式的锻炼和解决问题能力的提高，而不应当仅仅局限于概念的了解和运用。

在学习圆这一知识时，教师还可将圆与其他图形进行比较，让学生在比较过程中寻找圆的特性以及圆与其他类似图形的差异。曲边三角形虽然在定宽性上具有一致性，但是在其他方面仍旧有所区别。圆在滚动时以圆心为中心进行滚动，只需在圆心加一个轮轴，便可以驱动物体向前移动，但是曲边三角形在滚动过程中是以波浪式的曲线为中心向前移动。而椭圆与圆的不同之处在于椭圆具有长和宽，并没有定宽性。

图形与图形之间的对比与比较，能有效帮助学生理解图形的特性以及图形之间的区别，加深学生对于图形基本概念的理解，同样也能有效帮助学生更好地掌握图形知识，运用图形解决问题。

总之，教育学生学习数学知识并不是让他们局限在概念的理解以及掌握运用上，而是在于培养学生的思维模式以及帮助学生形成自主学习的良好习惯。实践是认识的来源、动力以及检验标准，数学知识是在历史的长河中经过不断锤炼而形成的。因此，学生在学习知识时应当有质疑的勇气，在课堂上，对于有疑问的地方就应当及时提出来。