考虑高铁时间窗和客户满意度的生鲜品公铁联运路径选择

李玉民，邱 梦，黑柏林，方曾利

(1.郑州大学 管理工程学院，河南 郑州 450001；2.郑州综合交通运输研究院有限公司，河南 郑州 450016)

近年来，在“互联网+”和新零售模式发展影响下，国内时令果蔬、冰鲜肉类等生鲜产品的消费需求日趋增长，生鲜电商产业发展呈现迅猛态势。伴随生鲜品需求量和运输量的增加，其供应链长、损耗率高等问题日益凸显。随着我国铁路运输结构性改革的深入推进，高铁快运业务开始出现并逐渐受到业界的青睐。2018年，京东和顺丰两大物流巨头分别与中铁快运合作，率先上线了“高铁生鲜递”和“高铁极速达”等运输服务产品，开展生鲜品寄递业务。虽然安全快速的高铁可以为生鲜品长途运输提供更高效的运力支撑，但我国已铺设的高铁网络线路尚不完善，公路运输辅助下的“高速公路+高速铁路”快速联运方式将成为生鲜品运输新的选择方向。因此，在高铁快运这一种新兴运输方式的参与下，如何选择生鲜品公铁联运的最优路径成为了亟需关注的问题。

路径规划和运输方式的优化组合是联合运输问题的关键，国内外学者在这方面的研究已经取得了较多成果，且大多以优化建模的方法展开[1-3]。随着考虑到的现实因素不断增多，多式联运路径优化的研究思路逐渐拓展。比如，考虑到运输需求的不确定性，于雪峤等[4]用三角模糊函数来描述不确定运量，构建了多式联运路径优化模型，并从运输路径和运输方式两个维度对广义最短路径进行决策；范厚明等[5]在不同的需求情形下用鲁棒性来研究需求不确定特征，分别构建多式联运网络内陆港随机选址模型和鲁棒性选址模型。当考虑到不同运输方式的固定运行时间和客户对收货时间的要求，一些学者将时间窗约束引入到路径优化模型中：Chang[6]研究各节点处运输方式的硬时间窗，采用启发式算法求解含时间窗的凹型运价率函数模型；Nossack等[7]分别考虑不同多式联运参与者的硬时间窗需求，解决了多式联运集装箱配送路线及空箱调度问题；此外，还有部分学者根据不同的运输对象和现实限制因素，分别考虑软时间窗[8]、混合时间窗[9]、模糊时间窗[10]等约束条件。

前述多式联运相关研究大多是依据公路运输、铁路运输、水上运输和航空运输构成的多式联运系统展开的[11-13]，鉴于高铁以及高铁参与货物运输均是新生事物，“高速公路+高速铁路”新型联运方式的路径研究还比较欠缺。其次，高铁运输的价值在于高时效性和高频次的服务，服务时间窗的存在会在一定程度上影响其路径决策，因此有必要把高铁服务时间窗考虑在内。另外，虽然已有一部分研究考虑到客户满意度[14]，但大部分集中于生鲜品配送路径优化问题，多式联运中考虑到客户满意度的文献较少，事实上随着消费者对生鲜品质和送货时限要求的提高，快速多式联运下的生鲜品质和时限保证也应逐渐引起重视。本文以“高速公路+高速铁路”运输网络为依托，从联运经营人的角度出发，用三角模糊数来描述生鲜品运输需求的不确定性，重点研究在高铁时间窗和客户满意度约束下的生鲜品公铁联运路径规划及运输方式的选择问题，为生鲜品快速多式联运提供路径决策参考。

1 问题描述

考虑模糊需求的生鲜品公铁联运路径优化问题描述如下。高速公路和高速铁路组成的运输网络为 G(V,A,K)。其中，V为网络中的运输节点集合；A为两点间的运输弧；K为运输方式集合。在此运输网络中，各高铁转运节点与各运输作业的收货节点均设有时间窗。另外，生鲜品运输需求具有模糊不确定性，在客户满意度约束下，以总成本最低为目标，选择各运输作业的联运路径和运输组合方式。

假设生鲜品在联运过程中符合以下条件：1) 公路与高铁均不存在运输能力和中转能力限制；2) 同一OD对之间货物不可拆分运输，即相邻节点间只能采取一种方式运输；3) 为了避免因运输环境变化而导致生鲜品质下降，将同一运输路径中的中转次数控制在3次以内，且节点内转运距离为零；4) 由于目前高铁货运还未配备专用集装箱，假设高铁采用无源蓄冷箱作为生鲜品运输基本单位。

2 模型构建

2.1 符号说明

具体参数及符号定义如下。

V ：联运网络中节点集合，其中， O、 D分别表示每条货流的起点和终点；

A：运输弧集合；

K：运输方式集合；

Z：路径总成本；

m：每箱生鲜品重量；

W：路径中转次数上限值；

ti：货物到达节点i 的时刻；

[ai,bi]： 节点i 的高铁服务时间窗；

ce：单个蓄冷箱单日维护成本；

ch：单个蓄冷箱单日租赁成本；

Tn：第n条货流的路径运输总时间；

δi：单位货物看管成本；

σtrs、 σtrf：时间敏感系数，分别表示在运输和中转过程中品质随时间变化的敏感程度，值越大，其品质越容易受时间影响而变化；

h：时间满意度约束值；

p：品质满意度约束值；

M：极大数；

另外，定义二进制变量。

2.2 模糊需求分析

现有的多式联运相关文献大多将运量设置为一定值进行优化建模[11-13]，但实际情况中生鲜品的运输需求往往具有季节性和波动性，使得物流企业规划运输路线时很难得到确定的运输量，然而物流企业可以根据历史订单得到生鲜品运输需求的变动范围。因此本文采用三角模糊数来表示生鲜品运量的不确定性。将生鲜品运量设置为三角模糊变量=(qmin,qθ,qmax) ， 其中，qmin、 qmax分别为最小、最大运量；qθ表示最可能出现的运量，隶属度为1。的隶属度函数 U表示为

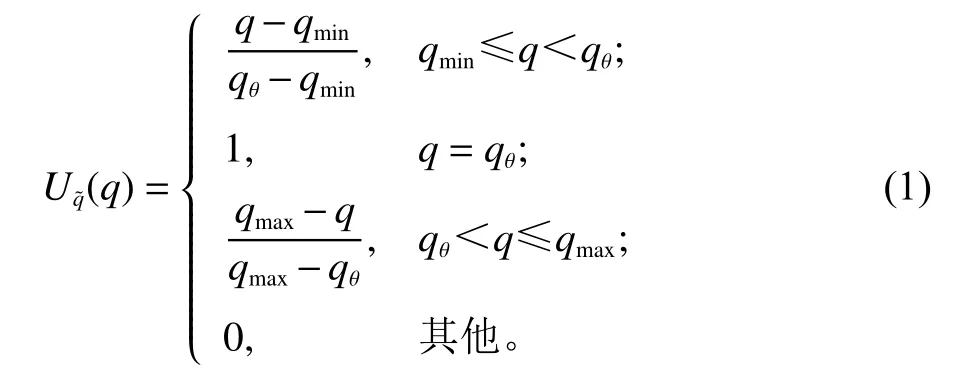
2.3 客户满意度分析

1) 时间满意度。相比普通货物，生鲜品的易腐特性决定了其对运输时间的要求更为苛刻。多数文献在考虑运输时限的同时通常以总时间最短为优化目标，但实际上需求企业存在计划的库存消耗周期，过早或过晚收货都会造成冷藏库存成本的增加[4]。图1为客户时间满意度与运输时限的关系，其中，[ET,E]为企业周转库存消耗期，此时期内企业仅保留维持正常经营的库存量，随着库存的消耗，生鲜品入库后产生的单位库存成本下降，时间满意度相应上升；[E,L]为最佳收货时间，时间满意度为100%；[L,LT]为企业的安全库存消耗期，当收货时间晚于L时将开始消耗安全库存，此时客户对库存消耗更加敏感，满意度下降明显。

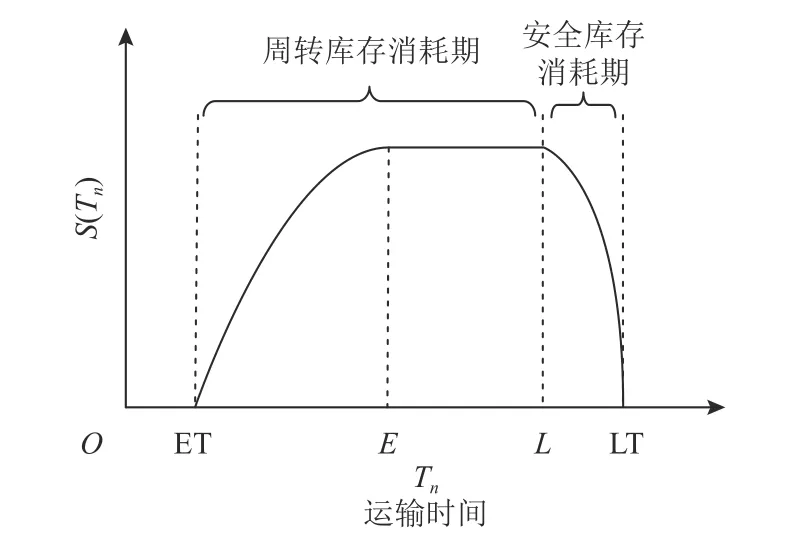
图1 时间满意度与运输时限关系Figure 1 Relationship between time satisfaction and transportation time limit

用隶属度函数 S(Tn)来 表示第 n个运输作业的客户收货时间满意度，如式(2)所示。

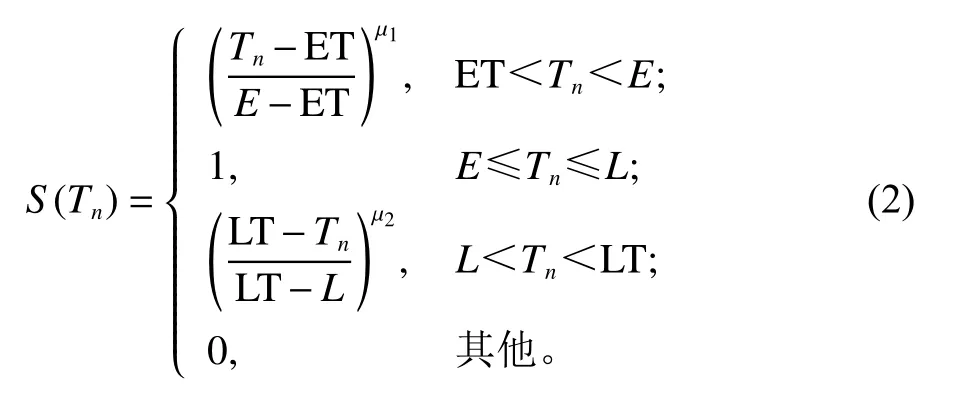
其中，µ1、µ2表示客户的时间敏感系数。

2) 品质满意度。除了运输时间要求，生鲜品在运输过程中的品质损耗也会导致客户满意度降低。本文在已有文献中腐败函数[15]的基础上进行改进，将运输环境变化造成的品质损耗考虑在内，来描述生鲜品运输中的总体品质变化情况。不同运输状态的稳定性不同，生鲜品时间敏感系数亦不同，设在途运输和中转两种状态下时间敏感系数分别为 σtrs、σtrf，则第n 个 OD对的生鲜品损耗率为εn=1−e−λ。其中，设客户可接受的损率区间为 [0,u]，此区间内客户满意度为100%；客户可容忍的损耗率区间为 [u,v]，此区间内客户满意度随损耗率增加而下降。品质满意度函数为

其中， γ为损耗率敏感系数。

2.4 高铁时间窗

高铁和公路的组织模式具有较大差距，公路运输灵活性强、可得性好，无固定时刻表，车辆可随时出发；高铁运输时效性强，安全性好，有固定的开行班次和时间窗。为了体现运输方式间的差异性，也使研究问题更贴合真实场景，本文在高铁运输节点处设置服务时间窗，提前到达高铁中转节点会产生一定的等待成本，迟到则需等待下一班列车服务时间窗开启。图2为高铁服务时间窗示意图。

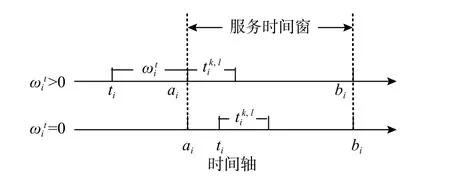
图2 高铁服务时间窗示意图Figure 2 The service time window of high-speed rail

对于到达时间，有以下3种情况。1) 早于时间窗到达时，即ti＜ai，此时还未开始服务，则有等待时间=ai−ti；2) 在时间窗内到达时，即ai＜ti＜bi，由于已经开始服务，所以不需要等待，则等待时间=0； 3) 晚于时间窗到达时，即 ti＞bi，由于同一节点有多时间窗开放，可以等待下一个服务时间窗开启，相当于早于下一个时间窗到达，可以按照第1种情况进行计算。

2.5 模型构建

根据以上模型描述，构建生鲜品公铁联运路径选择模型。

式(4)表示以联运总成本最低为目标，包括节点间运输成本、中转成本、等待成本和蓄冷成本；式(5)表示运输节点的货流平衡约束；式(6)表示同一批生鲜品运输过程中不可拆分，其中， (i,j)表示节点i 、 j间的运输弧；式(7)表示每个运输节点最多采取一种转运方案，或者不转运；式(8)表示货物在节点i中转时提前到达产生的等待时间；式(9)、(10)表示第n 条货流的运输总时间；式(11)为运输中转次数限制， W=3； 式(12)表示第 n条货流的时间满意度不低于h；式(13)表示第 n条货流的品质满意度不低于p；式(14)表示运输过程不能折返；式(15)表示在起点和终点不发生运输方式的转换。

3 模型清晰化处理

为了明确表达以上模糊变量，简化计算过程，将上述包含模糊运量的路径优化模型转化为模糊机会约束模型，得到等价清晰化表达式。本文采用模糊机会约束规划方法[16]，将具有模糊运量的单目标机会约束规划表示为

其中， f(x,y)为 目标函数， f¯为目标函数最小值；式(17)表示目标函数为最小值的概率要满足置信水平α， α ∈(0,1)。为了进一步将模糊机会约束规划模型转化为清晰等价式，对含有模糊变量的约束条件式(17)进行清晰化处理。

4 算例分析

4.1 算例设计

本文以哈尔滨等15个节点城市组成的联运网络为例，从起点开始依次标号为①哈尔滨、②长春、③通辽、④沈阳、⑤北京、⑥太原、⑦济南、⑧郑州、⑨西安、⑩武汉、⑪成都、⑫重庆、⑬贵阳、⑭长沙、⑮昆明，其公铁联运网络实际通达情况如图3所示。

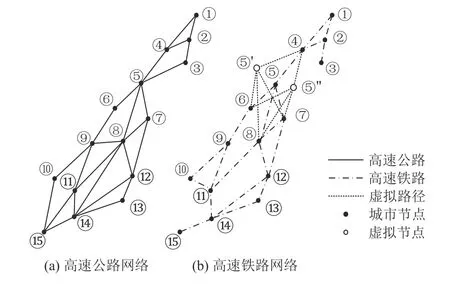
图3 公铁联运网络连通图Figure 3 Network of intermodal transport

为了使算例具有更好的实际参考性，算例参数均在现实调查数据的基础上测算并设定，数据调查时间截止到2019年10月。其中，高速公路运输的节点距离参照全国高速公路里程表；高铁运输节点距离参照12306官网高铁运营里程表。由于OD对的货流方向为单向，车辆通过节点的时刻按运输进程逐渐增大，因此高铁节点初始服务时间窗的设置遵循一定的顺序递增性，见表1。

表1 各节点高铁服务时间窗Table 1 The service time window of high-speed rail

随着城市间高铁开行班次的不断增加，单一的服务时间窗已不能满足实际研究需要，故本文在以往研究基础上增加了高铁服务时间窗的数量，并根据实际情况将时间窗间隔设为2 h，数量为5个。另外，为了方便计算，引入虚拟节点，将有时间窗约束的高铁节点的不同时间窗看作不同虚拟节点。例如，节点⑤的服务时间窗为[9.5,10]，根据班次的不同，可以将其分为⑤′、⑤″、· ··，其服务时间窗分别为[9.5+2,10+2]、[9.5+4,10+4]、[9.5+6,10+6]、· ··，将其他高铁节点也作此处理，没有时间窗约束的节点可将其时间窗表示为 [0,+∞]；虚拟节点⑤′和下游相邻节点⑥间的运输距离等于原节点⑤和⑥间的运输距离，即虚拟路径距离等于实际路径距离，如图3(b)所示。高速公路和高速铁路2种运输方式都取其平均旅行速度，高速公路为100 km/h，高速铁路为260 km/h，单位距离运输成本分别设定为0.6 元/(t·km)、3.2 元/(t·km)。

公铁联运网络中各节点单位货物中转时间及费用如表2所示。其他参数设置为 m=40 kg (含蓄冷箱)， δi=0.4 元/(箱·h)， ce=3元 /个， ch=12元/d，损耗率敏感系数 γ=0.5， 客户时间敏感系数 µ1=0.6，µ2=0.8， 生鲜品质变化时间敏感系数σtrs=0.001， σtrf=0.002 。初始置信水平 α =0.9， β1=β2=1。时间满意度和品质满意度约束值分别为h =0.7， p=0.6。

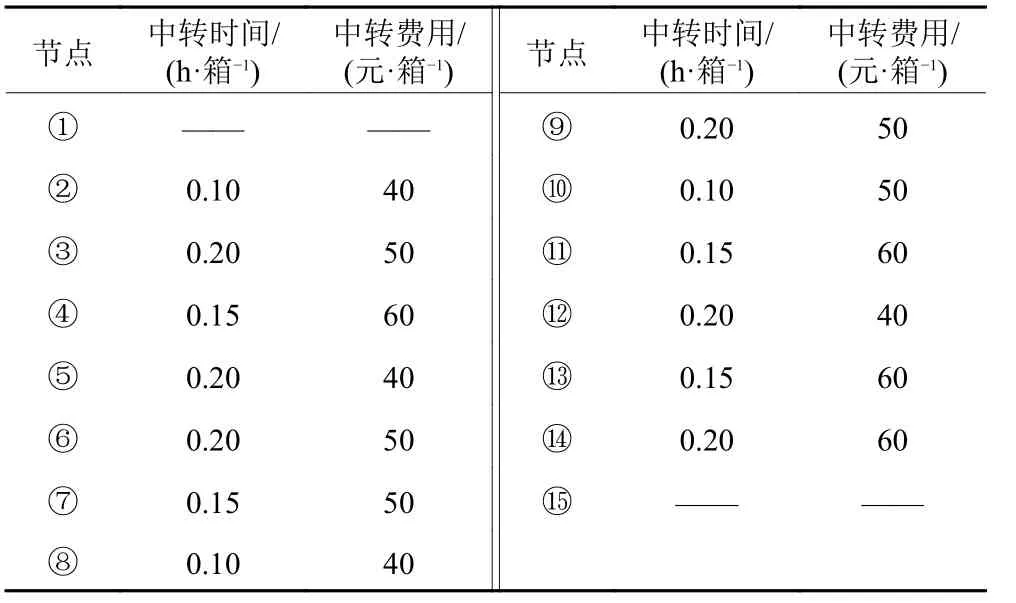
表2 各节点中转时间及费用Table 2 Transit time and cost for each mode of transportation

算例中各OD对模糊运量及品质满意度、时间满意度区间如表3所示。

4.2 结果分析

采用Lingo12.0对路径模型进行求解，解得各OD对最优路径及运输方式组合如表4所示。运输组合中“1”表示公路运输方式，“2”表示高铁运输方式，例如运输方式⑤→⑧→⑫→⑬的运输组合为“2 1 1”，则表示节点⑤到节点⑧采用高铁运输，节点⑧到节点⑫、节点⑫到节点⑬均采用公路运输。

表3 OD需求表Table 3 OD demands

表4 最优路径及运输方式组合Table 4 Optimal route and combination of transportation mode

考虑到生鲜品航空运输与高铁运输存在一定的相似性，两者都能提供小批量、高时效性和长距离的快速运输服务。为了比较公铁联运相对于单一运输方式的优劣性，选取编号为1的OD对为例，将高速公路、高速铁路和航空3种运输方式下的最优路径进行对比分析。其中，航空货运网络参考中国南航飞行里程表，如图4所示；航空货运单位运输成本根据实际情况暂定为高铁定价的150%，运行速度取800 km/h，其他参数及时间窗设置不变。计算及对比结果如表5所示。

图4 航空货运网络连通图Figure 4 Network of air transport

表5 公铁联运与其他运输方式对比Table 5 Comparison of road-rail multimodal transport mode with other transport modes

由计算结果可知，单一运输方式的优势和劣势均较为明显：高速公路运输成本较低，但εn和Tn均超出了客户可接受的最大范围，品质和时间满意度均为0；高铁运输速度快，总时间短，相比之下S(εn)最高，但到达时间过早，与客户的库存消耗周期不匹配而造成库存成本上升，因此时间满意度为0；航空运输与高铁运输的计算结果相似，且总成本较高铁运输更高。对比之下，公铁联运不仅能满足客户对生鲜品的品质和运输时间两方面要求，还能在一定程度上降低运输总成本，其优越性相比单一运输方式较为明显。

另外，为了进一步比较公铁联运相对于其他联运方式的优劣性，将其与“高速公路+航空”联运方式下的最优路径进行对比分析。由表5可知，“高速公路+航空”运输方式下最优路径的品质和时间满意度相比公铁联运略优，但总成本相比公铁联运高出12.19%。在现实情况中，货运航班常为点对点固定直飞，中途不停靠，且班次密度相对高铁较低，转运操作也更为复杂，因此在灵活性和衔接性上相比高铁有所欠缺；其次，航空运输易受天气影响，在安全性与准时性上也有所欠缺。各方面综合考虑下，生鲜品“高速公路+高速铁路”运输方式相对更优越，实现达成度上更可靠。当然，在实际决策中，联运经营人也可根据成本或满意度偏好在以上2种联运方式中作出合适的选择。

4.3 灵敏度分析

为了进一步探究各参数值变化对目标函数值的影响关系，基于模型约束条件中包含的模糊变量，分别对置信水平 α、品质满意度 p 和时间满意度 h进行灵敏度分析，结果如图5、图6所示。

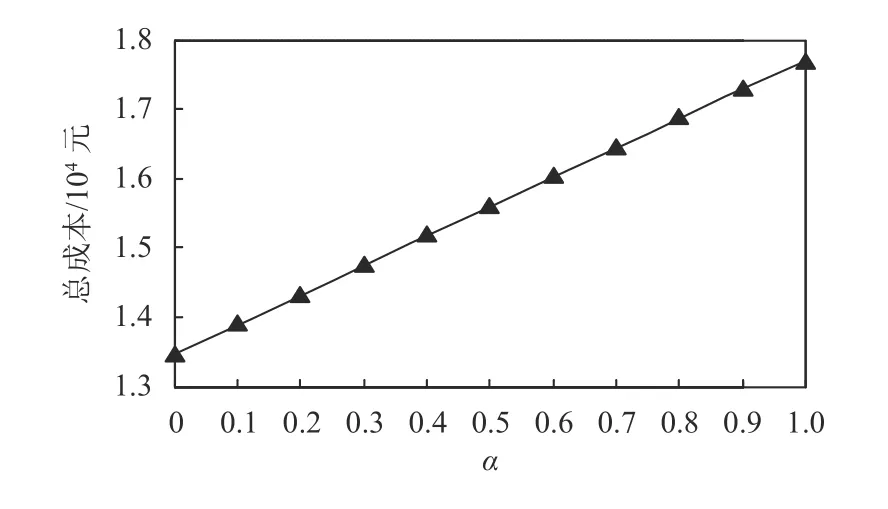
图5 α灵敏度分析Figure 5 Sensitivity analysis of α

图6 客户满意度 p 和 h 的灵敏度分析Figure 6 Sensitivity analysis of p andh

保持其他参数不变，改变 α取值，由图5可知，目标函数值随着 α增大而增大，表明在现实问题中，当客户对生鲜品运量需求的可信性增加时，总成本也会随之增加。当置信水平α =0时，总成本为13 460.21元，意味着此时联运经营人将不能满足客户的生鲜品运输需求，即需求不满足的风险为100%；当置信水平 α =1时，总成本为17 710.80元，此时联运经营人能完全满足客户需求，即需求不被满足的风险为0。

对客户品质满意度 p进行灵敏度分析，目标函数值变化如图6(a)所示。可知，当客户的品质满意度约束值 p≤0.5时，联运路径及其总成本基本不变，表明此时联运经营人提供的运输服务能充分满足客户在此区间内的对品质满意度的要求；当0.5＜p＜0.9时，总成本随着品质满意度要求的增加而上升，此区间内联运经营人必须通过改变运输路径和运输组合方式，不断提升运输服务能力来应对客户品质满意度要求的增加；当 p＞0.9时，受运输服务条件的限制，总成本趋于稳定，经营人所能提供的运输服务能力达到瓶颈。

同样，对客户时间满意度h 进 行灵敏度分析，目标函数值变化如图6(b)所示。由图可知，总成本变化趋势与图6(a)相似，不同的是，当 h ＞0.8时总成本已趋于稳定，数值为17 363.82元，且低于 p＞0.9时的总成本18 132.13元，说明在联运经营人保持同样运输服务能力的条件下，客户的时间满意度要求更容易得到满足。高铁在保证运输速度的同时开启了多个服务时间窗，增加了运输对象被服务的机会，更好地满足客户不同时段的收货时间要求。

5 结论

本文针对高铁参与下的生鲜品快速公铁联运问题，考虑生鲜品需求的季节性和波动性，将生鲜品运量作为一个模糊值，同时考虑到存在高铁服务时间窗和客户满意度的现实情况，构建了以总成本最小为目标的公铁联运路径选择模型。算例结果表明，相比较单一运输方式与“高速公路+航空”联运方式，“高速公路+高速铁路”新型联运方式能在满足客户各项满意度的基础上降低总成本，具有较好的适用性和现实操作性；通过灵敏度分析，分别得出置信水平和客户满意度约束值的变化对总成本的影响关系，为联运经营人提供实用性的路径参考。随着高铁开行网络的不断完善，在此基础上增加节点城市和OD对数量将是未来的研究方向。