相似性与置信系数为基础的推荐系统评分预测
2021-05-10王佳伟沈昱明
苏 湛,王佳伟,艾 均,沈昱明
(上海理工大学 光电信息与计算机工程学院,上海 200093)
1 引 言
用户在互联网上寻找合适内容的时候,往往会遇到海量的信息和物品,像是电影、书籍、商品等等.为了解决这类问题,推荐算法经常使用不同类型模型进行推荐系统中的评分预测或链路预测(将评分考虑成边连接,分值考虑成边权重)进行预测,然后预测权重或评分最高的物品推荐给用户.在此基础上,可以节省用户搜索物品所花费的时间.链路预测(包括评分预测)方法通常分为基于内容的算法[1]和协同过滤算法[2,3].
现实推荐系统中的评分预测通常结合基于内容的方法和协同过滤算法,以达到最佳的预测准确度.前者是充分利用用户的个人数据、物品内容、物品特征,根据用户以前喜欢的内容推荐对象[4].后者通过使用目标用户的历史评分生成推荐.
一般来说,推荐算法[5]通常分为3类,包括基于用户的算法[6]、基于物品的方法[7]和基于模型的方法[8].基于用户的算法在兴趣爱好或评分方面找出与目标用户相似的邻居,然后选择相似邻居喜欢的物品,并将其推荐给目标用户[9].
相比之下,基于物品的算法会找出目标用户喜欢的物品,找出与其相似的物品,然后过滤掉相似度低的物品,并向目标用户推荐相似的物品[10].此外,基于模型的算法首先基于历史数据构建模型,并使用该模型进行预测[11].
在这个过程中,相似邻居的选择有着重要的影响.许多学者对这一课题做了大量的研究.Ma等人提出了一种基于奇异值分解(SVD)符号的聚类方法来收集用户评分以外的社会信任信息,有效地解决了冷启动问题[12].Nikolaos Polatidi 等提出了一种基于协同过滤算法的多层次方法,通过共同评分的物品的数量,划分为不同的计算方法,更细腻地计算用户之间的相似性[13].徐毅等提出一种新的基于概率矩阵分解的推荐算法,运用信任关系与相似度获取用户之间的加权关系,从而提出一种融合用户信任度与相似度的推荐算法[14].
Liu等提出了一种新的节点相似度计算模型,即共同影响集.所提出的链路预测算法使用两个不相连节点的共同影响集来计算两个节点之间的相似度得分[15].尹永超等通过节点与其对应节点的邻居节点的结构相似度来计算节点对之间的连接概率,从而预测两个节点之间产生连接的可能性[16].
另一方面,由于物品和用户之间的复杂性,推荐系统通常被建模为复杂网络[17-19]模型.因此,人们通过网络科学进行了各种各样的探索以完成预测和推荐[20,21].以用户和物品为节点,以用户和物品之间的评分为边,利用复杂网络中的中心性、社团发现[22]等方法,对推荐系统进行建模和分析,并基于此对用户评分进行预测.
除了推荐系统之外,链路预测可以应用于更多相关领域.例如,研究人员可以使用链路预测算法向社交网络中的个人推荐潜在朋友.在生物网络中,链接预测算法可用于发现蛋白质之间缺失的连接,以防止高成本的实验[23].在这些预测过程中,预测的不单单是评分,而是节点间是否存在边.
通过对用户或物品的复杂网络进行建模,结果表明,该方法可以提高链路预测或评分预测的准确度,避免某类型的冷启动问题.例如,Ai和Su等人提出了一种基于空间分布模型的链路预测方法[20],基于物品共享标签相似度避免了物品冷启动问题.在这类方法中,还可以利用用户节点的属性和用户评分的行为对复杂网络进行建模,并基于多因素社区检测预测链路及其权重[24].作者认为,通过建立复杂网络模型和社区检测可以提高推荐系统预测的准确度.
另一方面,该领域中一些研究揭示了聚类也是一种有效的预测辅助方法.V.Subramaniyaswamy提出了一个基于语义的上下文挖掘推荐框架.在用户聚类过程中,采用自适应k近邻(AKNN)算法,通过选择合适属性提高预测准确度[25].除此以外,该文作者认为该方法能有效地解决了系统的可扩展性、稀疏性和冷启动问题.
一般的聚类方法比如kNN都是以一种指标作为聚类的指标,这样就受到单一指标的局限性,并且如果为每一用户进行聚类就需要花费大量的时间.
在现有的大多数工作中,用户之间的相似性是选择邻居的关键.领域内现有方法大多基于相似性选最高值选择k个邻居或kNN对邻居相似性进行聚类,选择其中的部分邻居是常见的方法.然而,该类型算法往往所需较多的邻居才能到达评分预测准确度的最优值,在大规模的推荐系统中,更多邻居意味着系统计算时间大增.同时,基于单一因素选择邻居必然存在一定误差,从而影响评分预测准确性的进一步提升.
本文的主要科学问题和贡献是针对目标节点与潜在邻居间的相似性和置信系数两个因素对其邻居进行聚类,从而为目标用户找到更加有效的邻居进行推荐系统评分预测.并通过研究复杂网络模型中的不同聚类和社团检测算法对评分预测过程中邻居选择的影响,研究了如何对邻居聚类的有效方法进行进一步的简化,以降低计算复杂度.本文的研究表明,在邻居选择中考虑相似度和置信度系数的情况下,最优评分预测准确性需要的邻居数量减少60%,并且最优预测准确性在邻居数量更少的情况下,准确性也得到提高.
2 算法设计
2.1 推荐系统定义与评分预测算法步骤
在本文研究的方法中,有m个用户和n个物品,它们分别构成了两个集合:用户集合U={u1,u2,…,um}和物品集合O={o1,o2,…,on},每个用户对其使用过的物品评分组成矩阵R={riα}∈Rm,n,其中riα表示用户i对物品α的评分值,评分范围在[1,5]之间取整数.为了方便知道某位用户是否对某件物品进行评分,设立矩阵A={aiα}∈Rm,n,aiα若为1表示用户i评价过物品α,为0则表示用户i没有评价过物品α.根据上面的信息构建一个用户-物品网络,ki和kα分别表示用户节点和物品节点的度值.
在上述推荐系统中,本文算法包含的主要流程如图1所示.
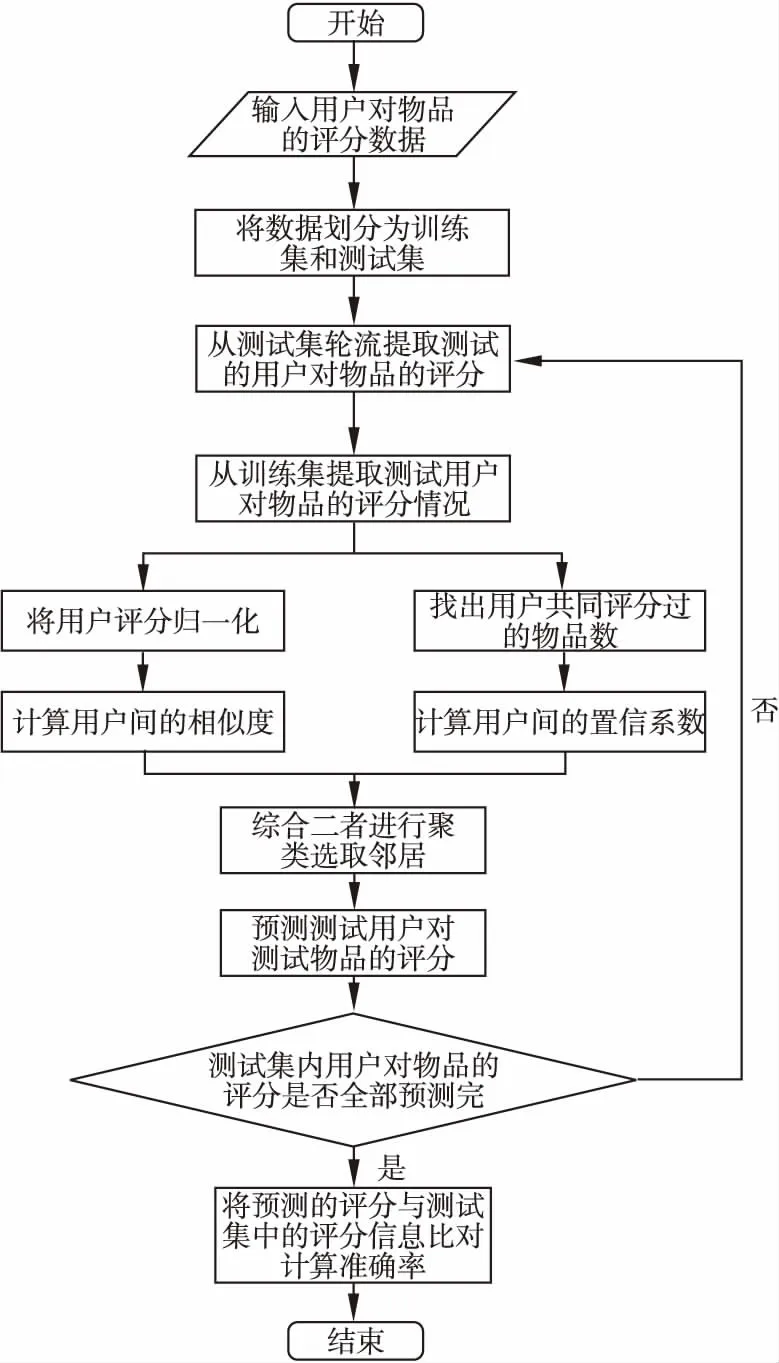
图1 推荐系统评分预测流程图
针对每个划分好的数据集,算法和核心步骤包括:1)从训练集中提取用户对物品的评分,然后进行归一化;2)基于归一化数据计算用户之间相似性与相似性的对应置信系数;3)基于相似性和置信系数结果对用户进行聚类;4)选择相似性和置信系数都较大的用户社团作为邻居;5)基于邻居预测目标用户对某物品的评分.
通过对给定集合中用户对物品的评分进行预测,算法对测试集中评分预测的结果可以用来度量算法预测结果误差,误差越小,算法性能越好.在实际系统中,对目标用户未评分的物品集合进行评分预测,再将预测评分最高的若干项物品推荐给该目标用户,就完成了推荐系统的推荐任务.
该算法中的步骤3)与步骤4)是其核心,与以往算法单独依据相似性进行邻居选择不同,本文算法应用相似度和置信系数两个参数进行邻居的选择研究.
基于相似度和置信系数,本文通过聚类方法对目标用户的潜在邻居进行分类,选出相似性核置信系数均较高的那一组用户作为邻居.随后对邻居聚类方法进行了进一步改进研究,以找出聚类效果最佳且时间复杂度较低的方法.最后在MovieLens数据集上对设计的多种方法进行了验证.
2.2 相似度和置信系数的定义
2.2.1 评分的归一化
相似度计算需要用户对物品的评分.但不同的用户可能对同一商品有不同的评分习惯.例如,一些用户有更高的要求,他们通常只会给出较低的评分.而另一些用户更随和一些,他们往往会给予更高的评分.为了减少来自用户的偏差,从[26]中采用了归一化的评分公式.
(1)
2.2.2 用户间相似度
本文中所用的相似性计算公式是李林志提出的基于传播的相似性公式[27]:
(2)
该相似性计算公式中ki表示用户的度,kα表示物品的度.归一化后用户i和用户j对共同评价过的电影α的评分越相近,共同评分过的电影越多,用户i和用户j越相似.例如有用户i,j,k3人,他们对电影的评分记录中最高分都为5分,最低分都为1分.他们对某部电影α的评分为3、3、5分.如果从这一条数据预测用户i对这部电影α的评分,通过公式(1)可以计算出归一化后的值为:eiα=0,ejα=0,ekα=1.通过公式(2)的计算结果可以看出用户j对用户i的影响为1,用户k对用户i的影响为0,用户j对这部电影的评分比用户k的评分更可靠一点.从公式的计算结果看出这符合用户评分的含义.
在原来相似度公式的基础上结合置信度系数f(n)得到新的相似度:
(3)
2.2.3 用户间置信系数
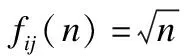
2.3 基于相似性与置信系数双因素邻居选择的评分预测
2.3.1 基于K-Means的双因素邻居聚类选择算法
其次考虑使用K-Means聚类来选取邻居.K-Means聚类是一种常用的“无监督学习”的算法,其目的是将n个观测值分成k个聚类,其中每个观测值都属于最近均值聚类.在其中一个集群中假设可信邻居用户,因为他们的相似性和信任系数应该相对高于其他邻居.
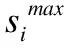
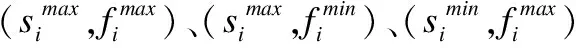
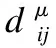
(4)
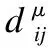
如图2所示Kmeans-2聚类结束后,样本集Xi会分成两个簇C1和C2,簇的质心分别为μ1和μ2,质心为μ2的簇C2相似度和置信系数较大,本文中选取C2内的数据作为评分预测邻居选择的范围.图2是以用户1为对象进行聚类后的邻居分布情况,圆形浅色节点为C2中的节点,菱形深色节点为C1的节点.图3是以用户1为对象进行聚类后的网络局部图,深色节点属于C2,浅色节点属于C1.
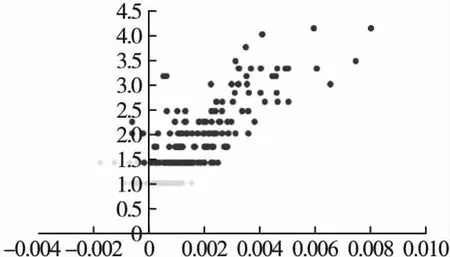
图2 以用户1为参照点进行K-Means聚类分布图
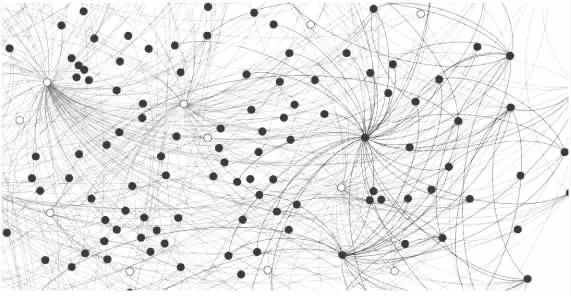
图3 以用户1为参照点进行K-Means聚类后的网络局部图
Kmeans-2聚类后C2内是否有充足的邻居这是一个重要的问题,文中将样本集Xi每次C2内的数据点数进行统计,依据数据点数出现的次数.可以从图4中看出聚类后C2内至少有42个邻居,因此Kmeans-2聚类后C2内有足够的邻居用来进行预测.
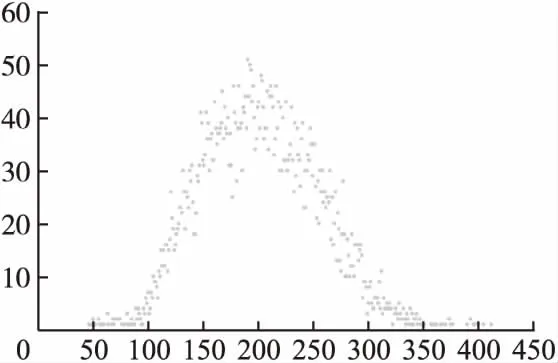
图4 针对各用户聚类后C2内邻居数分布点图
2.3.2 针对K-Means邻居聚类方法的改进研究
在对用户i进行聚类之后,C1中仍然有两种类型的邻居.本文称C1中相似度和置信系数较小的邻域为次要邻居.相比之下,其他C1邻居根据其与目标用户更高的相似度和置信度被称为主要邻居.换句话说,C1被分为两个子组.
为了详细分析两类邻居对预测结果的影响,进一步提高预测准确度,提出了基于Kmeans-2算法的主次邻居平衡方法.
2.3.3 降低聚类算法的时间复杂度
由于在上述的聚类过程中,每个用户都需要进行K-Means聚类,因此该算法比其他算法需要更多的时间来完成.为了减少时间消耗,本文提出了如下改进算法.
由于每个用户必须都需要重新进行聚类,因此K-Means聚类必须重复多次.降低复杂性的一种方法是在图2中为一组邻居设置阈值.任何相似度大于相似度阈值且置信系数大于置信系数阈值的邻居都被归为C1.该方法是对潜在邻居进行无迭代聚类,在实验部分称为简单聚类.在本文的工作中,本文选择了阈值来保持最大的40%和30%的相似性和置信系数.所以C1的邻居数与其他方法大致相同.
此外,如果本文把所有的目标用户和他们的邻居放在一起考虑,计算复杂度会大大降低.因此提出了一种基于整体的聚类方法.所有用户的所有邻居都放置在一个二维空间中,仅仅一次聚类就确定C1和C2.此方法在实验部分标记为All-Kmeans.
2.3.4 目标用户对物品的评分预测
通过相似度计算,通过公式(5)可以得到目标用户和目标物品之间的预测评分.值得注意的是,相似性是由公式(3)的方法给出的.
(5)
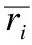
此外,在上面公式的基础上还可以进一步考虑1级和2级邻居,为此提出了公式(6):
(6)
其中n1是用户i邻居中主要邻居的数量,n2是用户i邻居中次要邻居的数量,W1和W2是设定的权值,它们之和为1.
3 实验和结果分析
3.1 数据集和预测准确性度量
为了验证本文提出的方法的有效性,本文利用MovieLens的数据进行了实验.该数据集包含671个用户、9125部电影和100004个用户的电影评分记录.用户的评分从1-5不等.此外,数据集被随机分成10组,并使用折10交叉验证,以确保结果在统计学上是可靠的[29].最终结果是10倍交叉验证中所有实验的平均值.本文从1,3,5,10,20,30,…,140-150中选择参考邻居的数量.
为了进行预测准确度的比较,文中引用了现有文献中基于用户的UOS和Pearson-RF方法.UOS方法是2017年发布的推荐系统中的链路预测方法.该方法将观点传播原理引入到链路预测中,考虑用户的评分习惯,根据用户的共享评分计算用户的相似度.Pearson-RF方法是一种改进的Pearson协作过滤算法[28],于2019年发表.近几年的方法仅仅考虑了相似性和置信系数作为预测的重要因素,而没有对潜在邻居进行聚类.因为UOS在2018的文献[30]中与领域内的各种新方法进行了横向比较,故可以作为参照,从理论上进一步推断本文算法的性能.
为了检验这些算法的有效性,本文使用了平均绝对误差(MAE)[31]和均方根误差(RMSE)[28].通过比较算法给出的实际评分和预测评分,发现MAE和RMSE越小,算法的效率越高.由于RMSE对预测误差进行平方处理,因此会对误差进行更严厉的惩罚.
(7)
(8)
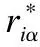
3.2 结果和分析
如图5所示,本文所有提出的方法,包括Kmeans-2、Kmeans0、Kmeans-2-30、All-Kmeans和Simple-clustering,都只需要非常少的邻居作为参考,就可以得到准确的预测结果.而Pearson-RF在预测中比UOS[29]更准确.
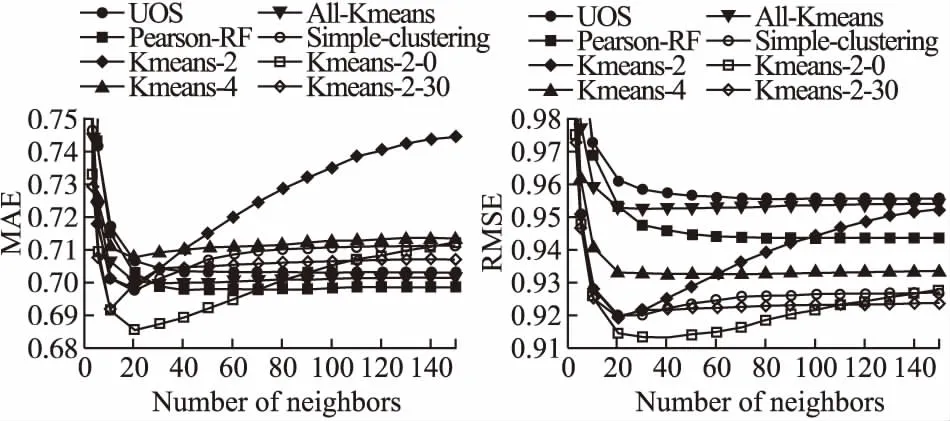
图5 各方法的MAE和RMSE结果图
令人惊讶的是,大多数算法只需要20个邻居就可以在MAE和RMSE中达到最佳准确度.相比之下,在MAE和RMSE中,UOS需要60个邻居和140个邻居,Pearson-RF则需要50个邻居和130个邻居.
总之,与其它的方法相比,通过聚类的方法在邻居较少的情况下达到了最优准确度,也就是说,Kmeans-2与Pearson-RF相比都将预测最优准确度的必要的邻居数量减少了60%和84.6%.与Pearson-RF相比,Kmeans0将必要的邻居数量分别减少了60%和69.2%,以做出最准确的预测.如果不需要计算复杂度并且使用简单的聚类,那么改进后的数目与Kmeans-2相同.
然而,本文所提出的方法不仅在所需邻居的数量上具有明显的优越性,而且在预测准确度上也有所提高.也就是说,在MAE值方面,Kmeans-2和Simple-clustering只需要20个邻居的就能与Pearson-RF需要50个邻居的预测准确度相同.在RMSE方面与Pearson-RF相比,Kmeans2和Simple-clustering的预测准确性分别提高了2.59%和2.49%.
在另一方面,Kmeans-2-0作为目前最佳的预测方法,与Pearson-RF相比,MAE和RMSE的预测准确性分别提高了1.71%和3.07%,所需邻居减少了60%.
对于Kmeans-2和简单聚类这3种方法,RMSE结果要优于Pearson-RF,而MAE结果几乎相同.这种现象背后的原因表明,基于邻居聚类的邻居选择可以避免推荐系统评分预测中的较大误差.
从曲线上看Pearson-RF如果只有20个邻居不足以得到最小的预测误差,由此推断用本文方法选择的20个邻居更可靠.
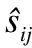
为了进一步探究公式(6)中的权重,图6给出了进一步的实验.这里使用Kmeans-2方法,将w1和w2设置为一对(w1,w2),即(1.0,0.0),(0.9,0.1),(0.8,0.2),(0.7,0.3),(0.5,0.5),(0.0,1.0),(1.2,0.1)和(0.8,0.1).
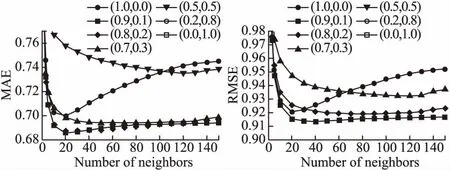
图6 不同权重的算法MAE和RMSE结果图
实验表明,给主次邻居给予不同权重,这种做法可以进一步提高预测准确度.具体地说,图6中的最让人接受的方法是通过w1=1.0和w2=0.0和来实现的.然而,在实验中图5中的结果相对较好的结果出现在当w1=0.9和w2=0.1时.因此,根据邻居的不同的重要性来区分他们是很重要的.
在一定范围内,主要邻居的权重越高,预测效果越好.当权重超过一定范围时,预测结果就会变差,特别是只参考主要邻居,不考虑次要邻居的时候,这时预测结果不是最佳结果.这种现象说明了次要邻居在预测结果中的重要性.低权值的次要邻居可以用来补偿修正主要邻居的预测趋势.
4 总结与展望
邻居的有效选择一直是评分预测和推荐算法中的一个重要课题.本文探讨了基于用户相似度和置信系数,提出了一种相似性与置信系数为基础的的推荐系统评分预测算法.
实验表明,即使在所需邻居数减少60%的情况下,该推荐算法仍可以达到最优评分预测准确度,揭示了置信系数和相似度这两个因素对于可靠邻居选择的重要性.通过基于置信系数和相似度的聚类,在所需邻居大量减少的情况下,该方法比对比方法预测的准确度高1%-3%.更重要的是,该方法能有效地减少了评分预测中的大误差.
研究表明,在预测和推荐中,两个用户之间共同评分的物品数量与其相似度同样重要.为了给目标用户选择最可信的邻居,用户间的置信系数和相似性都是必要的因素.
