FSD：增量压缩中局部特征表决的快速相似性检测

张露维，顾荣斌，李 静，李科心

1(国网上海市电力公司 信息通信公司数据运维中心,上海 200072)

2(南京航空航天大学 计算机科学与技术学院,南京 211106)

1 引 言

云计算、大数据和人工智能技术的快速发展，对海量数据的存储、传输及备份问题提出了新的挑战.数据规模的快速增长对数据存储技术提出了更高的要求，也使得海量数据的存储、传输和备份成为当前的研究热点之一.如电力领域，随着泛在电力物联网的不断提出，各个业务领域的系统、数据等可能会面临大量的存储、传输及备份等工作.由于巨大的数据量，如何对这些业务系统的数据进行有效的存储、备份关系到整个电力系统的安全稳定运行.

数据压缩是指在不丢失信息的前提下，缩减数据量以减少存储空间[1，2]，提高传输、存储和处理效率的一种技术方法.数据压缩通常需要以重复数据删除为基础，其关注的主要是重复数据删除，而当数据之间不包含重复但又高度相关的时候效果较不明显.增量压缩作为一种面向非重复而又高度相似数据的压缩方法在云计算、容灾备份等领域受到越来越多的重视.它通常以块级别进行识别和检测相似性数据，利用安全指纹技术[3]提取相似数据的共同特征，实现对数据的压缩，其过程主要包括原始数据的重复数据删除、相似数据检测、共同特征提取、差异性特征提取及存储基准数据和数据之间的映射关系等5个步骤.其中，相似性检测是增量压缩的核心步骤.相似性数据检测的工作为增量压缩提供了压缩候选集，其检测的结果为增量压缩提供输入数据.

在数据块相似性检测方面，Broder[4]提出一种N-transform Super-Feature方法(简称“SF方法”)，但是该方法需要花费较多时间对提取到的数据指纹信息进行转换从而得到数据特征，因此效率受到限制.需要花费较多的时间进行特征转换，导致获得数据特征的时间复杂性较高.Zhang Yucheng[5]等人提出一种基于数据局部信息的分组方法进行数据的相似性检测，但在利用数据块局部构造超级特征时，特征分组策略不较明确.另外，该方法在进行特征分组的时候需要对特征的大小关系进行排序，导致额外的时间开销.针对上述研究在数据块的相似性检测方面存在的问题，本文基于数据局部特征构建了一种快速的特征提取方法FSD(Fast Similarity Detection)，通过将提取到的特征进行分组和集成以获得超级特征，从而实现对数据块的快速相似性检测.本文提出的基于数据块局部特征集成的快速相似性检测方法FSD降低了提取特征的开销，提高了增量压缩中相似性检测的效率，实现了对数据的高效增量压缩.

本文章节安排如下：第1节介绍了增量压缩中相似性检测存在的问题；第2节介绍了增量压缩的相关工作；第3节介绍了增量压缩中基于局部特征集成的快速相似性检测方法FSD；第4节中结合公开数据集，通过对比实验验证了FSD的有效性；第5节对本文方法FSD进行总结以及未来的研究方向.

2 相关工作

数据压缩作为一种能够减少数据存储规模的技术在图像压缩、数据存储、文件传输及容灾备份系统中的应用受到越来越多的关注[6-10].用于减少和消除非重复但却高度相似数据块之间数据冗余的增量压缩技术是数据压缩中较为流行的一种技术.增量压缩可以最大化地减少压缩损失[11]，因此被广泛使用在数据库存储[12-14].通常增量压缩利用相似性数据检测技术实现对于数据的压缩，相似性数据的检测通常需要对数据进行划分，根据数据块的大小可将增量压缩划分为整文件检测技术[15]、数据块检测技术[16].对于数据块相似性检测技术而言，又可以进一步分为固定长度分块检测技术[17]、基于内容的变长分块检测技术和滑动窗口检测技术[18].对于整文件检测技术而言，其检测相似性数据以文件为基本单位，检测粒度过粗，不能很好地检测出文件内部的相思相数据.固定长度分块检测技术在进行数据块划分的时候不用过多考虑数据内容，分块较为简单，数据处理速度较高，固定大小的分块有利于存储和管理分块.但其分块边界是由绝对偏移量决定的，当插入或者删除数据时，会产生数据块边界偏移问题.基于内容的变长分块检测技术解决了插入、删除数据边界偏移的问题，使新增和删除操作影响的区域被控制在很小的范围内，保证更多的相似性数据被检测出.但该方法数据块的大小是变化的且波动较大，这会导致数据块的存储和处理更加的复杂.基于滑动窗口的数据块相似性检测通过逐字节滑动的方式检测相似性数据，可以获得很好地压缩比.该方法进行分块的时候是固定大小的，存储和管理更加方便.但该方法在每一个可能出现重复数据块的位置均要进行分块查询，时间性能较差.相似性检测主要用于寻找候选的压缩对象.SF方法是目前最为流行的数据块级别的相似性检测方法，该方法首先获取数据块的特征，然后根据数据块的特征进行相似性检测.虽然该方法能够最大程度地检测到高度相似的数据块，但需要进行大量的线性转换以获取数据块的特征.后来基于局部特征的相似性检测Finesse方法被提出，相比于SF方法，该方法在数据块相似性检测的速度和效率上提升了2-3倍，且提高了压缩效率.但该方法构建超级特征不够明确，需要对特征进行排序.Zhang Y等人[11]提出一种基于缓存备份流来解决增量压缩中的额外计算开销的问题.增量压缩是建立在无重复数据的基础上的，因此在某些备份系统中就需要考虑重复数据删除以及数据压缩的平衡问题.Min Fu等人[19]提出一种在备份工作负载中平衡重复数据删除的数据压缩方法.Xia W等人[20，21]提出了基于内容的变长分块相似性检测技术的重复数据删除和利用备用数据流的细粒度局部性特征来加速增量编码的方法.已有的增量压缩方法在对数据进行压缩时需要提取数据特征，对数据特征进行重组、转换实现数据相似性检测，然后对相似性数据进行编码以减少存储资源的占用.在数据块特征提取时，已有方法大多存在特征提取过程复杂、计算开销大等问题.对于以上问题，本文提出一种基于局部特征集成的快速相似性检测方法FSD，用于实现对数据块特征的高效提取及相似性数据块的高效检测.

3 FSD：基于局部特征集成的快速相似性检测

随着信息时代的不断发展、数据的不断积累，数据规模的快速增长对数据存储技术提出了更高的要求，也使得海量数据的存储、传输和备份成为当前的研究热点之一.增量压缩作为一种能够改善海量数据存储、备份的技术不断得到学者的重视.SF方法虽然在一定程度上解决了增量压缩中数据特征的提取和相似性检测问题，但是其仍然存在特征提取过程耗时等问题.针对相似性数据检测过程中存在的特征提取耗时、特征分组不明确、检测效率低等问题，本文提出一种基于数据块局部特征集成的快速相似性检测方法，优化了数据特征的提取的过程；利用数据特征的分组集成，实现了对数据块的快速相似性检测.基于局部特征的快速相似性检测方法的整体架构如图1所示.

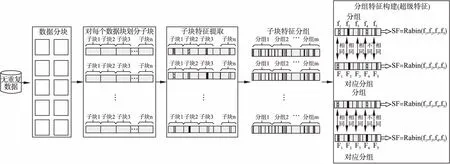
图1 基于局部特征表决的快速相似性检测框架

该方法是一种基于增量压缩的快速相似性检测方法主要用于检测非重复但高度相似性的数据块，以便为增量压缩提供候选输入数据集.本文方法实现对数据块的相似性检测的大致过程为：

1)对原始无重复数据集进行数据块的划分，通常数据块大小为4KB级别；

2)将划分好的数据块再次进行数据子块的划分，以便利用数据块的局部信息实现相似性检测；

3)对划分好的子数据块进行特征提取，其中本文使用改进之后的SF方法实现对子数据块特征的提取；

4)对提取到的子数据块特征进行集成表决，根据表决的结果构建超级特征；

5)将数据块间对应的超级特征进行对比，实现相似性数据块的检测.

3.1 数据块局部特征提取方法

SF方法作为一种相似性检测方法在增量压缩领域被广泛使用，其在增量压缩过程中主要负责数据块之间相似性检测工作，并且为后续的数据压缩提供候选数据.对于给定大小的数据块，SF方法从其中提取固定数目的特征，然后将其中的特征按照顺序进行分组以形成超级特征，然后根据构建的超级特征来进行相似性数据块的检测.该方法对数据块进行特征提取的过程为：

先根据安全指纹提取技术(一种滚动哈希算法[3])获得某个长度为L的数据块位于j位置的数字指纹信息，然后再将利用一对随机值mi和ai对数字指纹信息进行转换以便获得该数据块的一个特征，即：

(1)

其中，Rabinj是位于j位置的滑动窗口的Rabinj指纹，对于具有一个或多个相同特征的数据块可能非常的相似，数据细微的更改不会对数据的相似性带来很大的干扰.

接着继续从不同的位置开始执行上述操作，以获得N个特征Feature[N].然后对获得的N个特征按顺序固定特征数目分组以形成超级特征，即：

SFx=Rabin(Featurex·k,…,Featurex·k+k-1)

(2)

对于相似的数据块之间仅有非常微小的一部分不同，因此他们的特征以及SFx应该是相同的.这种方法能够很好地进行高度相似数据块之间的检测的原因是：首先，SFx的匹配意味着数据块之间的很对特征是相似的；其次，多个SFx被用于数据块之间的相似性检测.因此，更多相同和相似的SFx能够保障相似的数据块被检测出来.

对于以上方法，虽然其能够在一定程度上进行相似数据块之间的检测，但是其在进行数据块特征提取的时候需要消耗额外的转换工作将Rabin指纹转换成特征.另外，由于其对子特征的分组是按照顺序进行的并且将组内所有的特征都用于构建超级特征.当组内差异性特征较多的时候，这种方法形成的不同超级特征可能会是相似的，这样不利于对相似性数据块的检测.针对SF方法存在的问题，本文提出一种改进的数据块特征提取、分组方式.文献[5]中提到，相似数据块之间的局部信息也是相似的，因此，本文将数据块进行二次划分形成更小的数据块，然后进行子数据块特征的提取，进而对子数据块的特征进行分组表决，具体的执行过程如伪代码所示：

算法：改进的SF方法提取特征

输入：数据块的内容str；数据块的长度L

输出：N个特征，feature[N]

1.子数据块长度L/N

2.fori=0 toN-1do

3.feature[i]=0

4.form=0 toN-1do

5.forj=m*L/Nto(m+1)*L/N-1do

6. 获取子数据块的Rabin指纹FP=RabinFunction(str,m*L/N+j)

7.iffeature[m]<=FPthen

8.feature[m]=FP

9.endif

10.endfor

11.endfor

对子数据块进行特征提取的过程首先是减少了对Rabin指纹的转换过程，从而降低了特征提取过程的时间开销；其次，实现了对固定大小子数据块的特征提取，有利于对子数据特征进行分组从而构建超级特征.

3.2 基于局部特征集成的快速相似性检测

针对SF方法在数据块特征提取过程中存在的计算特征时间消耗较多、特征分组可能导致差异性数据块具有较高相似性问题.本文提出了一种改进的SF方法，降低对数据块特征提取的时间开销.另外，基于改进的SF方法，本文提出了一种面向增量压缩的基于局部特征集成的快速相似性检测方法，该方法可以实现对相似性数据块的快速检测，进而提高增量压缩的效率、降低增量压缩过程的时间开销，其具体的过程如图1所示.本文的快速相似性检测方法主要是基于增量压缩的整个过程的，下面基于增量压缩的过程将具体介绍本文方法每一步的执行过程.

1)数据块的划分，本文基于增量压缩的局部特征集成的快速相似性检测主要实现对无重复但高度相似的数据的相似性检测.因此，本文所用数据基于重复数据删除之后的数据集，然后将该数据集划分为4KB大小的数据块.

2)接着将划分好的数据块再次进行数据子块的划分.文献[5]的研究表明，数据块之间的相似性可以由数据块局部信息之间的相似性来表示，并且两个相似的数据块之间的局部信息表现为按顺序的高度相似性，具体可由图2表示.因此，本文在4KB级别数据块的基础上再进行划分，将4KB大小的数据块划分为更小的数据子块，以便利用数据块的局部信息实现相似性检测.对于数据块进行子块划分的做法是将数据块划分为若干个大小相同的子数据块.

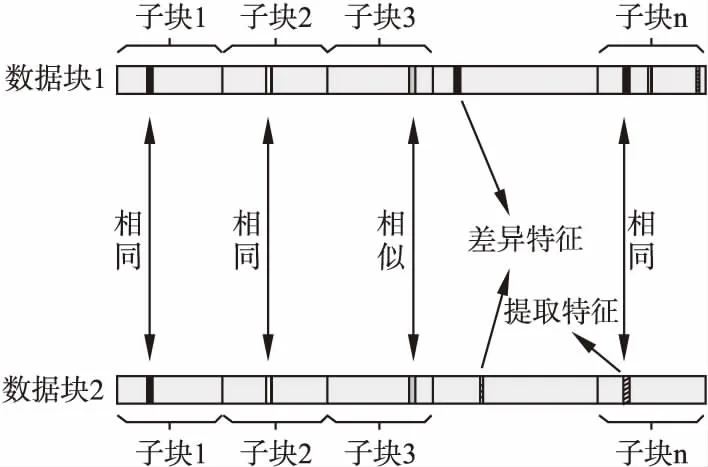
图2 相似数据块局部信息之间的关系

对于数据块的相似性检测工作，本文通过获取子数据块的特征，然后对特征进行分组以便形成超级特征，然后利用超级特征进行数据块相似性检测，其中的相似性检测依据和集合间相似性检测依据类似.两个集合之间相似性的计算方法为：对于两个集合A和B，H(A)和H(B)分别是A和B中元素的散列对应的集合，其中H是从一个极小的排列独立族中均匀随机地选取的.集合中的一个元素被映射到一个整数.令min(S)表示整数集合S中最小的元素，则：

(3)

上面的定义指出，集合A和B具有相同的最小哈希元素的概率与它们的相似系数相同.

3)子块划分完成了对4KB大小的数据块的二次分割，形成了更小的数据块(或称为局部数据).接下来需要完成对子数据块特征的提取以及子数据块特征的分组工作，其中子数据块特征的提取工作，本文使用改进的SF方法，如表1所示，其中子数据块特征分组形成超级的特征的方式如图3所示.

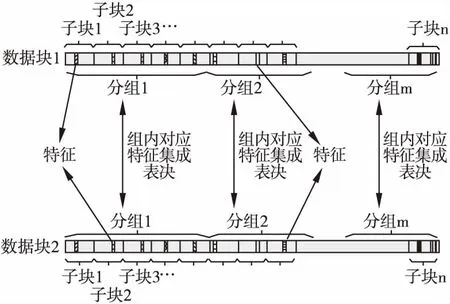
图3 数据块局部特征分组方式

如图3所示，获得数据块的局部特征之后，接下来需要对局部特征进行分组，本文选择将若干个连续的局部特征分为一个组，从而将数据块的所有局部特征分为不同的组别.

4)对数据块的局部特征进行分组之后，接下来需要完成超级特征的构建.对于超级特征构建问题，本文利用分组内的若干个特征通过集成的方式构建，在构建超级特征的过程中采用了集成表决的方式，具体过程如图4所示.对于数据块A中的分组和数据块B中与之对应的分组而言，其超级特征的构建过程为：

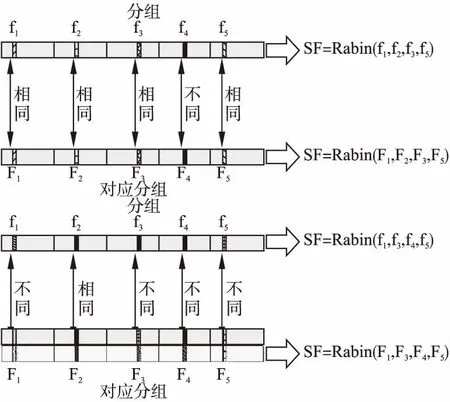
图4 分组特征的构建方式

a)按原始顺序排列数据块A和数据块B对应分组之内的若干个局部特征，即：

(4)

b)计算数据块A和数据块B对应分组中局部特征是否相同，构建sij表示数据块A中的局部特征和数据块B中的局部特征，即：

(5)

然后记录相同的特征个数Sum_same及不同的特征个数Sum_diff，即：

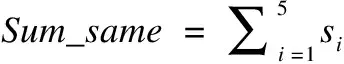
Sum_diff=5-Sum_sanme

(6)

c)如果相同特征个数大于相异特征个数，则利用相同的局部特征构建分组的特征，构建方式如图4所示.如果相同特征个数小于相异特征个数，则利用相异的局部特征构建分组的特征，构建方式同上.

当数据块的所有超级特征构建完成之后，即可对数据之间的相似性进行检测，相思相检测的方法和上文所述的集合之间测相似性检测方法相同.

4 实 验

为了对本文方法FSD的有效性进行验证，本文利用公开增量压缩领域的数据集进行实验.在验证FSD方法的有效性时，本文基于开源的原型系统Destor[19]对增量压缩的整个过程分别进行了不同层面的实验.

4.1 实验配置

基于Ubuntu16.04系统、8核Intel i7-8565U处理器、Intel i5-9400处理器和一个1TB的硬盘等构建实验环境，利用开源的重复数据删除原型系统Destor实现增量压缩，以此来验证本文方法的有效性.本文实验建立在重复数据删除之后的数据集之上，因此增量压缩的过程可以简单的分为3个部分，首先是相似性数据块的检测，然后是共同特征提取和差异性特征的提取，最后是建立数据块之间的映射关系以实现数据的增量压缩.对于第一个部分即相似性数据块的检测工作，利用本文方法首先将数据块划分为固定大小的子块，然后提取子块的特征以及子块特征的分组.由于对子块特征分组时采用了集成表决的思想，本文选择将5个子块作为一个分组，然后将对应5个子块的特征进行表决，以便于减少表决时同票数的冲突.

4.2 实验数据集和衡量指标

实验所用数据集来自典型应用场景下的增量压缩数据集，其中包含了网络快照、数据库快照、虚拟机映像、tarred源代码文件等等，实验数据集具体信息如表1所示：

表1 实验数据集

表1中DR(Deduplication Ratio)表示重复数据删除率，其可由公式(7)计算:

(7)

其中DSB表示重复数据删除前的数据大小，DSA表示重复数据删除后的数据大小.由于本文相似性检测方法需要建立在重复数据删除后的数据集之上，因此需要对原始的数据集进行重复数据的删除工作.对于相似性检测性能的衡量，本文选择增量压缩比DCR(Delta Compression Ratio)和增量压缩效率DCE(Delta Compression Efficiency)两个指标进行比较.其中DCR根据增量压缩前的数据大小和增量压缩之后数据的大小之商计算得出，DCE根据增量压缩后数据块的大小和增量压缩前的数据块大小之比计算得出.DCR在一定程度上反映出增量压缩后存储空间的节省程度，DCE用于检测本文方法检测到相似性数据块之间的相似度.根据DCR和DCE的定义可知，DCR侧重的是总体空间节省，而DCE则强调检测到的类似数据块块本身，更高的DCE说明检测到的相似性数据块更精确.

4.3 实验结果

实验1.相似性检测效率对比

为了更好地进行相似性检测效率，本文在上述6个数据集上分别进行10次实验，并将10次实验求得的平均值作为最终的结果进行比较.实验中，本文选择将经典的数据块相似性检测方法SF方法、Finesse方法以及本文方法进行比较，实验结果如表2所示.

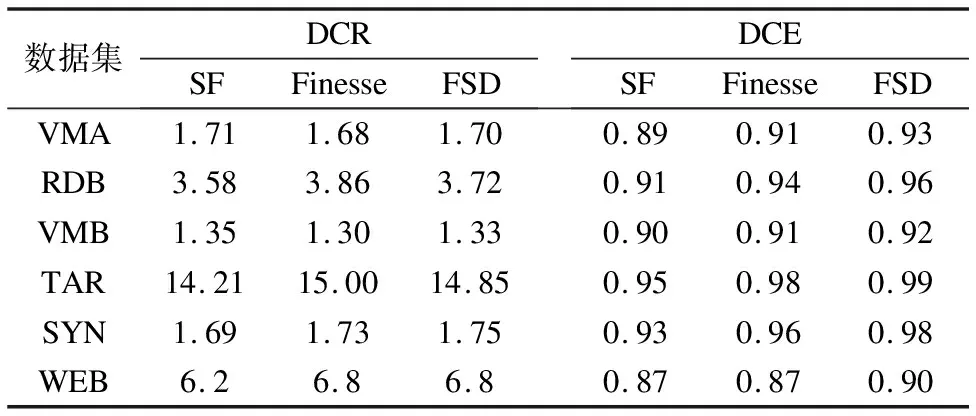
表2 不同数据集上数据块相似性检测效率比较

DCR主要用于描述数据经过压缩后数据压缩的程度.Finesse对于数据压缩的过程，经过了数据划分、数据块子特征提取、超级特征的构造等过程，该过程虽然在整体上实现了对数据的高效率压缩，但是Finesse方法对数据特征提取的过程计算复杂性大，需要额外的特征转换开销.本文方法FSD首先提取了一种快速的数据特征提取方法，然后基于该快速数据特征提取方法构建了一种基于数据特征集成表决的快速相似性数据检测方法.由于本文方法改进和简化了数据特征的提取，所以在相似数据检测方面得到了显著性的提升.但是对于DCR而言，Finesse要适当优于本文方法FSD,这种优势是通过牺牲特征提取的效率换得的.就整体而言，本文方法在DCR表现方面相比于Finesse稍微不足，但DCE方面表现较为理想.

实验2.形成超级特征速度的对比

对于形成超级特征速度的比较，本文选择在不同配置的机器上进行对比，最终比较的数据是通过多次实验并求取平均值得到.这里，本文选择Intel i7-8565U处理器、Intel i5-9400处理器作为代表进行构建超级特征速度的比较.由于本文方法在计算特征和特征分组的时候不需要额外的转换操作并且形成分组的时候不需要对特征进行排序和选择操作，所以本文方法在构建超级特征的时候速度较快，其具体的对比如图5所示.

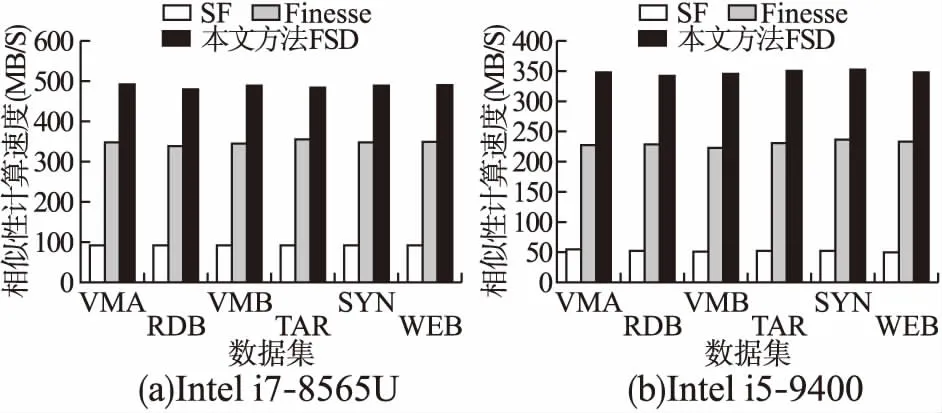
图5 相似性计算速度的比较

图5中，本文基于不同的处理器配置进行了数据块相似性计算速度的比较.在相同配置的条件下，本文方法在相似性计算的速度方面优于其他两种方法.对于SF方法而言，其在计算特征的时候需要额外的线性转换操作，因此执行速度相对较慢.而Finesse方法在计算特征时减少了线性转换工作，但是其在进行特征分组的时候需要按照一定的顺序对特征进行排序，故其执行的速度也不如本文方法.

实验3.系统吞吐量的对比

由于本文方法在进行相似性数据块的检测时候是以整个增量压缩为基础的，因此，对于系统吞吐量的比较，本文选择以增量压缩实现的整个过程进行对比，其中包含了重复数据删除、相似性数据检测、共同特征的提取以及建立相似性数据块之间的映射关系等.对于增量压缩执行过程中系统吞吐量的对比，本文也是基于不同的硬件配置进行比较，具体执行结果如图6所示.

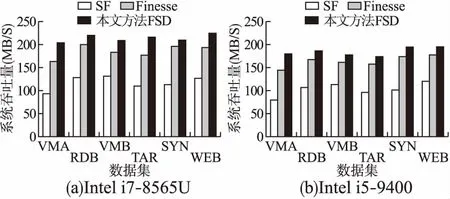
图6 不同相似性数据块检测方法的增量压缩系统吞吐量的对比

从图6中可以看出，本文方法在不同配置的机器上系统整体吞吐量都要优于另外两种方法，其根本原因在于增量压缩过程中相似数据块检测阶段的不同.由于本文在进行相似性数据块检测的时候利用了数据块局部特征以及对特征进行了有效、快速的分组，从而提高了对相似性数据块的检测效率.

为了达到更好的增量压缩效果，本文方法基于局部特征集成的快速相似性检测方法(FSD)需要建立在重复数据删除之后的数据集上.我们将本文方法FSD同时应用在重复数据删除之后的数据集和没有删除重复数据的数据集上进行对比.实验中，本文选择Oracle数据库上的测试数据作为待压缩数据，测试FSD方法在两种不同数据集上的压缩效果，结果如图7所示.

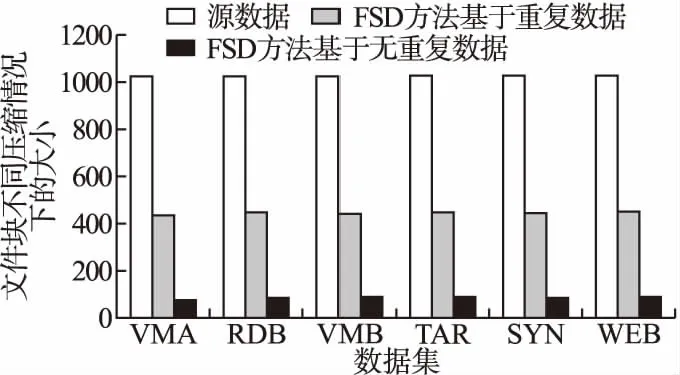
图7 本文方法在重复数据集和无重复数据上压缩效果对比

5 结束语

对于增量压缩中相似性数据块检测过程中面临的特征提取耗时、计算开销大、检测效果不好等问题.本文以增量压缩为背景，首先提出一种改进的数据块局部特征提取方法，实现了对数据块局部特征的快速提取.然后基于该数据块局部特征提取方法，提出了一种基于数据块局部特征集成的快速相似性检测方法.该方法首先将数据块划分为若干个子数据块，然后利用改进的数据块特征提取方法提取子数据块的特征，接着对子数据块的特征进行按顺序分组，以便利用集成的思想构造超级特征，最后利用构造的超级特征实现对数据块的相似性检测.实验结果表明，本文方法能够有效降低数据块特征提取的时间开销、提高相似数据块的检测效率，进而提高增量压缩的执行效率.本文方法在构造超级的特征的时候利用了分组的思想，本文所设计的分组相对来说较为简单，下一步需要深入探究子数据块的分组问题.