改进孪生神经网络的控制图模式识别方法
2021-05-10刘青星黄海松姚立国
刘青星,黄海松,姚立国,胡 耀,3
1(贵州大学 机械工程学院,贵阳 550025)
2(贵州大学 现代制造技术教育部重点实验室,贵阳 550025)
3(贵州人和致远数据服务有限责任公司,贵州 550025)
1 引 言
控制图是基于统计学原理,对生产过程中关键工序参数或产品质量特征观测值[1]进行统计分析,判断制造系统是否处于稳定可控状态.当制造过程出现不稳定因素时,控制图便会产生异常波动,反映出制造系统中的异常因素.生产者根据控制图波动模式采取相应措施,消除生产过程中的异常因素,控制产品质量的稳定性.过去对控制图的识别依赖生产者的经验,难以实现对控制图模式的实时识别,有碍于智能制造产业的发展.随着机器学习和深度学习算法的兴起,对控制图异常模式识别不再依赖于传统的控制界限或人的经验,而是运用机器学习、深度学习等智能算法识别控制图的异常模式.
在机器学习领域,识别控制图异常模式的步骤为:特征提取、维数简约、分类器选择等.首先提取控制图包含的质量特征,主要包含统计特征[2]、形状特征[3]、小波分解特征[4]等.再对质量特征进行融合,如统计特征与形状特征融合[5]、统计特征与原始数据融合等.质量特征融合后,融合特征的维数较大,常利用PCA、KPCA、KECA[6]、ICA[7]等降维算法进行特征简约,最后使用支持向量机[8]、极限学习机[9]、随机森林等分类器对控制图特征进行识别.使用机器学习方法对控制图进行特征识别时需要人工提取质量特征,忽略了数据之间的关联性,容易出现过拟合.
由于深度学习对大数据具有很好的分类效果,且无需人工提取数据特征,能很好的运用特征之间的相关性对控制图进行模式识别.因此,卷积神经网络[10]、迁移学习[11]、脉冲神经网络[12]等深度学习的方法也被运用于控制图的识别.深度学习虽然大样本数据集下有很好的识别性能,但是对样本量较小的情况识别精度低,不适用于小批量多品种生产过程中的控制图识别.
孪生网络是度量学习中的一个重要手段,通过度量样本之间的空间距离,识别出样本的分类,在数据量较少时,表现出良好的分类性能,常用于目标跟踪[13]、文本分类[14]、图片分类[15]等方面.由于统计过程控制(Statistical Process Control,SPC)的应用在很大程度是对生产制造过程的稳定性进行监控,使得异常控制图样本较少,异常模式较多,深度学习的方法难以准确识别异常控制图.针对上述问题,本文提出的基于PCSNN的控制图异常模式识别模型,通过度量控制图样本的空间距离,衡量控制图样本间的相识性,从而实现对控制图的异常模式识别.随着生产制造过程的持续,影响生产过程稳定性的异常因素增多,控制图异常模式的样本量也随之增多,PCSNN模型的识别率也优于其他深度学习方法;同时,在生产制造过程中,产品品种的改变会引发控制图特征参数变动,在此情况下,PCSNN模型也能较好的识别出控制图的异常模式.
2 控制图的基本模式
控制图的基本模式由美国西部电气公司首先提出,共有8种,如图1所示,分别为正常模式(Normal,NOR)、循环模式(Cyclic,CYC)、上升趋势(Uptrend,UT)、下降趋势(Downtrend,DT)、向上阶跃(Upward Shift,US)、向下阶跃(Downward Shift,DS)、系统模式(Systematic,SYS)、分层模式(Stratification,STR).控制图的异常模式,有着各自的表现形式,并代表着生产过程的不稳定状态与各种异常因素.控制图的基本模式在生产过程中可用公式(1)进行描述:

图1 控制图基本模式
x(t)=μ+d(t)+r(t)
(1)
式中,x(t)是t时刻控制图的观测值;μ是产品质量特征的平均值;d(t)是制造系统中的异常因素所引发的异常模式,当制造系统处于稳定状态时,则认为d(t)为0;r(t)是制造系统中正常的随机波动,制造过程处于稳定可控状态时,r(t)服从正态分布.
3 孪生神经网络

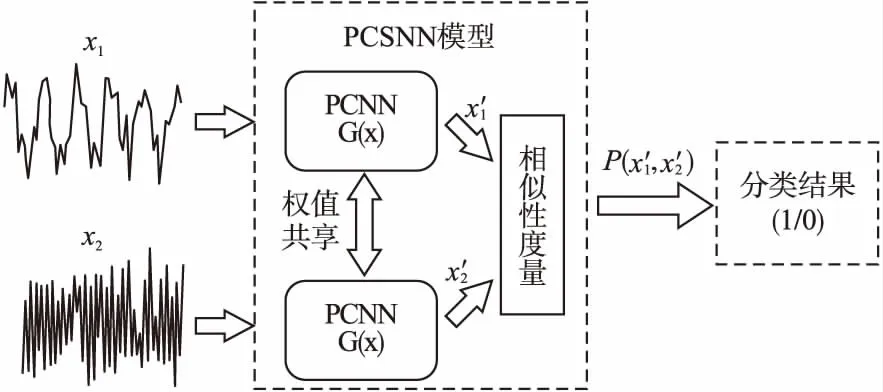
图2 基于PCNN的孪生网络
3.1 One-Shot K-Way分类
S={(x1,y1),(x2,y2),…,(xk,yk)},k (2) (3) 如图3所示,多层感知器(Multilayer Perceptron,MLP)是通过非线性激活函数和多层神经网络实现样本数据的非线性表达,学习数据特征的非线性关系. 图3 多层感知器 如图4所示,卷积神经网络通过对原始数据进行填充零元素、卷积、池化、展开特征图等操作.通过将卷积窗口与数据特征进行卷积运算获取卷积特征,并用激活函数对卷积特征进行非线性映射,获得原始数据所包含的数据特征. 图4 一维卷积神经网络 在实际生产中,控制图的异常样本较少,且异常模式较多,同时控制图样本的数据点一般较少,卷积神经网络等深度学习算法难以获得控制图所包含的非线性特征,对控制图的识别率较低.本文基于孪生神经网络的思想,提出适用于小样本的控制图模式识别模型PCSNN,如图2所示.所设计的孪生网络的分支网络PCNN如图5所示.首先使用两层感知器将控制图样本映射到高维空间,增加控制图质量特征的维数,解决了因控制图样本的质量特征数据点较少导致深度学习方法难以提取特征的问题;使用4层一维卷积神经网络提取控制图所包含的非线性质量特征,利用孪生网络的思想,实现小样本情况下控制图的模式识别. 图5 PCNN模型 用于控制图样本维数升维的两层感知器的激活函数均为Relu函数,第1层感知器包含了100个神经元,先将样本维数为(60,1)的控制图映射为(60,100);第2层感知器包含了500个神经元,将质量特征映射为(60,500);为了一维卷积神经网络能够提取控制图的质量特征,对映射后的质量特征张量进行维数转换,转换为(30000,1)的张量. 通过卷积网络获取控制图样本的非线性特征,第1、2个卷积层使用较大的卷积窗口初步提取控制图特征,卷积窗口尺寸分别为16×1、10×1,卷积窗口数量均为16个.第3、4个卷积层使用较小的卷积窗口尺寸进一步提取微小的特征,卷积窗口尺寸均为3×1,卷积窗口数量分别为32和64.一维卷积神经网络在每次完成卷积运算后都通过Relu函数对卷积特征进行映射,再进行最大池化处理,池化窗口为2×1.全连接层包含100个神经元,将一维卷积网络所提取的特征图通过sigmoid非线性映射函数映射为(100,1)的特征. 3.4.1 质量特征的相似性度量 孪生神经网络对质量特征进行相似性度量,即:计算两个样本相似的概率,一般常用的方法是:①使用公式(4)计算控制图质量特征向量的空间距离DG(x);②通过公式(5)将控制图特征向量的空间距离DG(x)映射为样本相似概率P(x1,x2). DG(x)=‖G(x1)-G(x2)‖ (4) P(x1,x2)=sigm(DG(x)) (5) (6) 式中G(x)为PCNN模型. 3.4.2 PCSNN神经网络的loss函数与优化函数 PCSNN使用Adam函数作为优化函数.PCSNN的loss函数为正则化的交叉熵函数,如公式(7): (7) 式中y控制图样本对是否相识的标签,相似则为1,不相似则为0;P(x1,x2)为控制图样本对(x1,x2)的相似概率. 为了验证PCSNN模型的有效性,从两个方面对PCSNN进行实验验证:①将PCNN,MLP模型与PCSNN进行对比,对比不同训练样本量下PCNN、MLP、PCSNN模型的识别率.PCNN模型如图5所示,直接使用全连接层提取的特征进行控制图的异常模式识别,并使用Adam优化器优化PCNN模型;MLP模型使用了5个隐藏层,分别包含200,200,200,200,100个神经元,隐藏层的激活函数均为ReLU函数,且使用Adam优化器对模型进行优化.②对比了PSCNN模型在质量特征参数变动时的识别率.分析在不同训练样本量下,质量特征均值与质量特征方差两个参数变化时,对PCSNN识别率的影响. 为满足对比实验的需求,利用Monte-Carlo方法按表1的控制图参数对8种控制图模式进行仿真.共仿真9个训练样本集,分别包含40,80,160,240,400,800,1200,2400,4000个控制图样本,每个样本包含60个数据点,每个样本集有8种分类,如表2所示,控制图均值μ=50,标准差σ=5. 表1 控制图参数 根据表2,使用表1的控制图参数,仿真2组测试集A、B,每组9个测试集,每个测试集中包含8种控制图基本模式,每种模式有25个测试样本,共计200个测试样本.由于A5、B5仿真时均值为50,方差为5,故而A5、B5测试集为同一个,同时也是MLP、PCNN、PCSNN对比试验的测试集. 表2 测试集的均值与方差 本节将A5作为测试集,分别测试在9个不同训练样本量下,PCSNN、MLP、PCNN的识别精度,测试结果如表3所示.PCSNN是基于度量学习的思想,衡量样本对之间的相识性,是小样本学习中的一个重要方法.如表3所示,在小样本情况下,PCSNN的识别精度高于PCNN与MLP方法;同时,随着样本量的增加,PCSNN、PCNN、MLP的识别精度都有显著的提升.这是由于深度学习方法容易受样本量的影响,在小样本情况下,PCNN与MLP学习效果不佳.随着样本量的增加,深度学习方法从数据获取到更多的分类信息,从而提高了样本的识别率.而本文提出的PCSNN将深度学习与度量学习的思想结合,利用深度学习方法提取数据特征,再利用孪生网络的思想构建能够度量样本类别的多维空间,因此,随着样本量的增加,深度学习方法提取了更多的样本特征信息,扩大了不同样本间的空间距离,进一步提高了PCSNN的识别率. 表3 PCSNN与其他两种方法测试结果对比 在多品种小批量的制造模式下,质量特征的改变主要体现在质量特征均值或方差的变化.为了验证孪生网络模型在不同品种下对控制图的识别精度,本节使用PCSNN对A、B两组质量参数变动的测试样本进行识别. A组测试集的均值由46向54逐步递增,方差为5,对应的PSCNN测试精度如表4所示.B组测试集的方差由3向7逐步递增,均值为50,对应的PSNN测试精度如表5所示.分别对比表4与表5发现如下规律:1)在训练样本量相同的情况下,A1-A9或B1-B9的测试精度总体呈现‘峰形’,即测试样本的均值或方差与训练样本的质量特征参数(μ=46,σ=5)相同时测试精度最高,测试样本的测试精度随着质量特征参数‘背离’训练样本质量特征参数的‘距离’增大而降低;2)绝大多数情况下,对于相同的测试集,随着训练样本量的增加,测试精度逐渐增大;3)PCSNN在训练样本较少时,具有较高的识别率和较强的泛化能力. 表4 样本均值变动下PCSNN测试结果 表5 方差变动下PCSNN测试结果 PCSNN将样本特征映射到多维空间,通过算法迭代将相似样本的空间距离缩小,扩大异种样本的空间距离,从而构建了判断样本对是否相似的非线性映射,并通过One-shot8-way的方式,将待分类样本与基于训练集构建的支持集进行相似性判断,实现样本的分类.当控制图样本质量参数发生改变时,该控制图样本与训练集样本的相似性概率降低,但通过One-shot eight-way的方式,PCSNN选择与训练集最大相似概率的样本分类作为待分类样本的类别.因此,在控制图样本的质量特征参数发生变动时,PCSNN依旧保持较好的识别率. 本文提出的PCSNN模型,解决了在样本量较少、识别类别较多时的基本控制图模式识别问题.该网络主要有两个结构相同、权值共享的神经网络构成,通过判断控制图样本对是否相似,从而识别控制图基本模式.通过使用不同样本量的控制图样本,对MLP、PCNN、PCSNN进行训练,分析了3个模型的测试精度,发现在控制图的样本较少情况下,PCSNN模型比MLP、PCNN模型展现出更高的识别精度;而随着样本量的增加,PCSNN的识别率也比MLP、PCNN高;通过质量特征参数变动下PCSNN测试精度对比实验,发现在产品品种发生改变时,引发控制图的特征参数变动的情况下,PCSNN展现出良好的泛化性能,对控制图的模式识别表现出较高的识别率.3.2 多层感知器
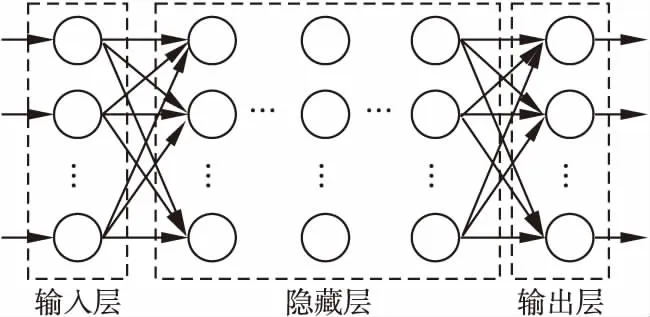
3.3 一维卷积神经网络

3.4 控制图模式识别模型


4 实验验证
4.1 实验设计


4.2 PSCNN与MLP、PCNN的对比实验

4.3 质量特征参数变动下PCSNN测试精度对比实验


5 总 结
