三种一致性分析模式的比较研究——以2020 年高考数学全国卷Ⅱ（理科）为例

付 钰 高胜前 綦春霞

一、研究背景

教育系统中的各要素必须协同工作， 以对学生学习产生积极促进作用[1]。教育中一致性的思想萌芽于新行为主义处于鼎盛时期的20 世纪60 年代初。而国内关于一致性的研究起步较晚，以“一致性”为主题词在中国知网检索发现，研究成果于2010 年开始呈现增长趋势，主要集中于教材以及试题（中、高考试题）与课程标准的一致性[2-6]。

2001 年，教育部关于印发《基础教育课程改革纲要（试行）》的通知中明确指出：“国家课程标准是教材编写、教学、评估和考试命题的依据，是国家管理和评价课程的基础”。[7]故对高考试题与课程标准的一致性分析将对我国考试评价的发展提供启示与借鉴。但是通过检索的文献，国内学者多数运用Webb、SEC、Achieve 模式进行一致性分析，也有少数学者构建一致性的测评工具， 如方全波根据调研所得评价要点，构建了一致性评价指南[8]，刘思构建了以教学意识和教学行为为坐标轴的直角坐标系， 通过调研数据对应点的象限分布分析二者的一致性[9]。

由此可见，教学内容、学业评价、试题、教材等与课程标准的一致性研究是课程评价的热点话题，研究者采用的Webb、SEC、Achieve 模式研究工具较为成熟，且进行了本土化改造。但是关于研究工具比较分析的文章则很少见，故明晰研究工具之间的异同，对我国一致性研究具有重要的意义。 根据国务院办公厅印发的《关于新时代推进普通高中育人方式改革的指导意见》，2020 年起，实施普通高中新课程的省份不再制订考试大纲[10]。 而《普通高中数学课程标准（2017 年版）》于2018 年1 月第一次印刷，故高考试题中会渗透课程标准的理念与高考命题建议，因此本文将以2020 年高考数学全国卷Ⅱ（理科）与课程标准的一致性为例， 探究Webb、SEC、Achieve 模式的异同。

二、研究设计

1. 研究对象

本文选取《普通高中数学课程标准（2017 年版）》（以下简称课程标准） 与2020 年高考数学全国卷Ⅱ（理科）进行一致性研究。

2. 研究工具

（1）Webb 一致性分析模式

Webb 一致性分析模式是由美国学者诺曼·韦伯（Norman Weber）提出的，用以判定学业评价是否与课程标准具有一致性[11]。 该模式主要从“知识种类”“知识深度” “知识广度”“知识分布平衡性”探究学业评价的测试内容是否在课程标准规定的学习内容范围内，具体如表1 所示。

表1 Webb 模式评价标准[12]

（2）SEC 一致性分析模式

在Webb 模式基础上， 美国学者安德鲁·波特（Andrew Porter）和约翰·史密森（John Smithson）等人共同研发了SEC 分析模式 （Surveys of Enacted Curriculum）[13]。 该模式肯定了知识内容与知识深度维度是研究一致性重要的组成部分[14]，即构成了“内容主题×认知水平”的矩阵，故又称“二维矩阵法”。SEC 模式操作首先是对要研究的两个项目的知识内容和认知水平进行整理和分析，建立二维矩阵，然后再把表中统计的数据转变成总比率为1 的比率表。 最后通过这个模式，进行一致性的计算与分析，根据计算结果进一步判断两个项目要求的匹配程度。 其中波特一致性系数的数学计算公式为：

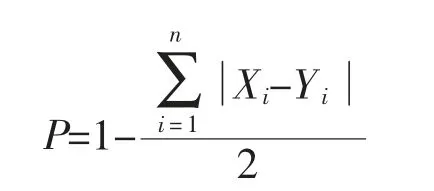
在波特一致性系数P的数学计算公式中，n表示矩阵中的单元格数，i表示矩阵中的某一指定单元格。Xi、Yi分别表示矩阵X和矩阵Y中的第i个单元格的值。 波特一致性系数P的范围是0～1，当P=0 时，表示两者一致性差异最大，当P=1 时，表示两者完全一致，即一致性水平最高[15]。

（3）Achieve 一致性分析模式

美国非盈利教育研究机构Achieve 组织的罗斯曼（R. Rothman）等人在借鉴Webb 模式经验的基础上，开发了新型的“测验——标准”一致性分析工具，并在应用的过程中不断完善和发展[16]。该模式是以“向心性” “挑战性” “均衡性”三个维度分析学习内容与考试试题的一致性，“向心性”说明试题与对应学习目标在学习内容、认知水平上的一致性，“挑战性”关注试题设计是否科学、聚焦试题的操作层面的水平，“均衡性”即试题覆盖课程标准的内容要求的范围以及涉及的学习目标的单位， 具体如表2所示。

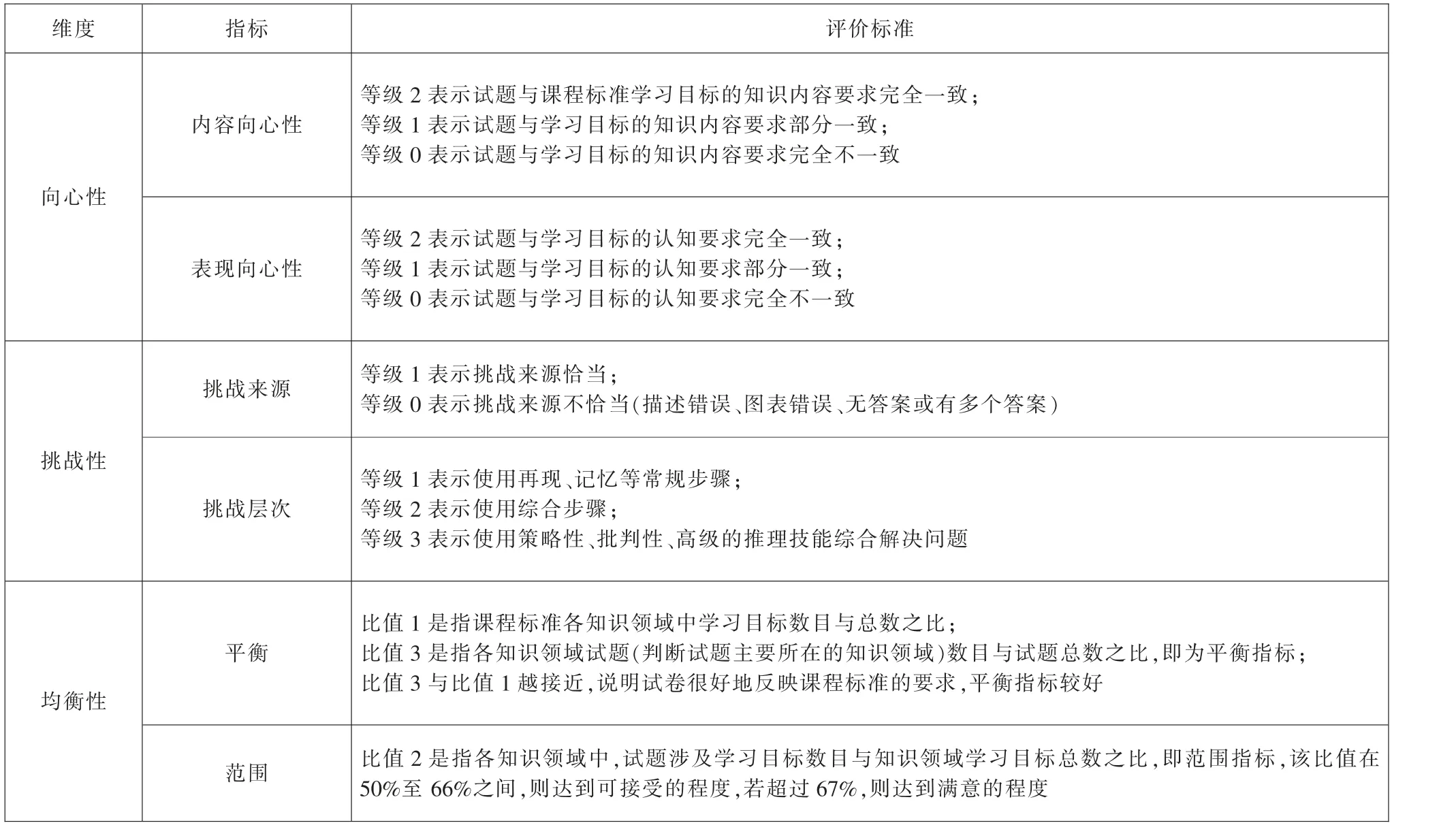
表2 Achieve 模式评价标准[17]

由上述可知， 三种一致性分析模式存在一定的差异。 首先，SEC 模式具有试题与课程标准的整体一致性水平，Webb、Achieve 模式没有整体的一致性测量水平。 其次，从分析维度上看，SEC 模式无法在细节上处理一致性相关程度，Webb 模式从知识种类、知识深度、 知识广度、 知识平衡性分析一致性，Achieve 模式从向心性、 挑战性及均衡性三个维度，内容向心性、表现向心性、挑战来源、挑战层次、平衡、范围六个子维度分析一致性，呈现的一致性的结果较为具体。 最后，Webb、SEC 模式一致性水平有确定的参照临界值， 但Achieve 模式没有确定向心性、挑战性一致性可接受的标准。

3. 研究流程

首先对2 位数学课程与教学论研究生进行一致性模式评价标准的培训， 然后由1 位数学教育博士和2 位数学课程与教学论研究生分别对课程标准和试题进行独立编码，并利用SPSS 25.0 计算其肯德尔相关系数，结果表明肯德尔秩相关系数为0.8743，说明评分者间信度较高。 然后由1 位数学教育专家对编码进行审核，对3 人不一致的编码进行讨论，最终形成统一的编码表。

4. 主题分类

结合课程标准中课程内容的划分， 研究者将部分数学内容进行整合，如数列、三角函数均属于函数内容，不等式可看作函数应用问题，故将其归为函数与导数这一主题。因为向量与解析几何、立体几何有密切关系，故将其分为解析几何与平面向量、立体几何与空间向量2 个主题。其次，概率与统计可作为独立的主题。故本文确定的4 大内容主题为：函数与导数、解析几何与平面向量、立体几何与空间向量、概率与统计。 本研究只分析课程标准中必修课程与选择性必修课程， 选修课程的内容不作为本文的研究对象。此外，课程标准中教学目标分为：知识技能、数学思考、问题解决、情感态度，由于学业水平考试较难测验到学生的数学思考、情感态度等，故本文只分析知识技能的内容要求。同时，课程标准内容要求标有*的内容为选学内容，本文不将其作为研究内容。

三、2020 年高考数学全国卷Ⅱ（理科）与课程标准的一致性分析

1. 基于Webb 模式的2020 年高考数学全国 卷Ⅱ（理科）与课程标准的

（1）试题编码示例

例1：设O为坐标原点，直线x=a与双曲线C：的两条渐近线分别交于D，E两点，若△ODE的面积为8，则的焦距的最小值为（ ）

A. 4 B. 8

C. 16 D. 32

本题选自2020 年高考数学全国卷Ⅱ（理科）第8题，属于函数与导数、解析几何与平面向量主题，涉及的知识种类为“掌握基本不等式”“结合具体实例，能用基本不等式解决简单的最大值或最小值问题”“了解双曲线的简单几何性质”共三条课程标准中的具体内容要求。该题符合课程标准中“掌握基本不等式”“结合具体实例， 能用基本不等式解决简单的最大值或最小值问题”的内容深度要求，高于“了解双曲线的简单几何性质”的内容深度要求。本题涉及运用双曲线渐近线等相关知识点解决问题， 高于 “了解”的认知水平。

（2）基于Webb 模式的2020 年高考数学全国卷Ⅱ（理科）与课程标准的一致性结果

在编码中， 以每道题目所涉及的知识模块为研究对象，若1 道题涉及2 个主题，则记为2 个题目。例如，全国卷Ⅱ理科第8 题涉及基本不等式、双曲线知识，分别属于函数与导数、解析几何与平面向量2个主题，则记为2 道题目。全国卷Ⅱ理科高考试题编码结果如下：函数与导数主题有14 道题，解析几何与平面向量主题有7 道题， 立体几何与空间向量有6 道题，概率与统计知识主题有5 道题。 综上，全国卷Ⅱ理科高考试题题目总数为32 个。 基于Webb 模式的一致性分析结果如表3 所示。

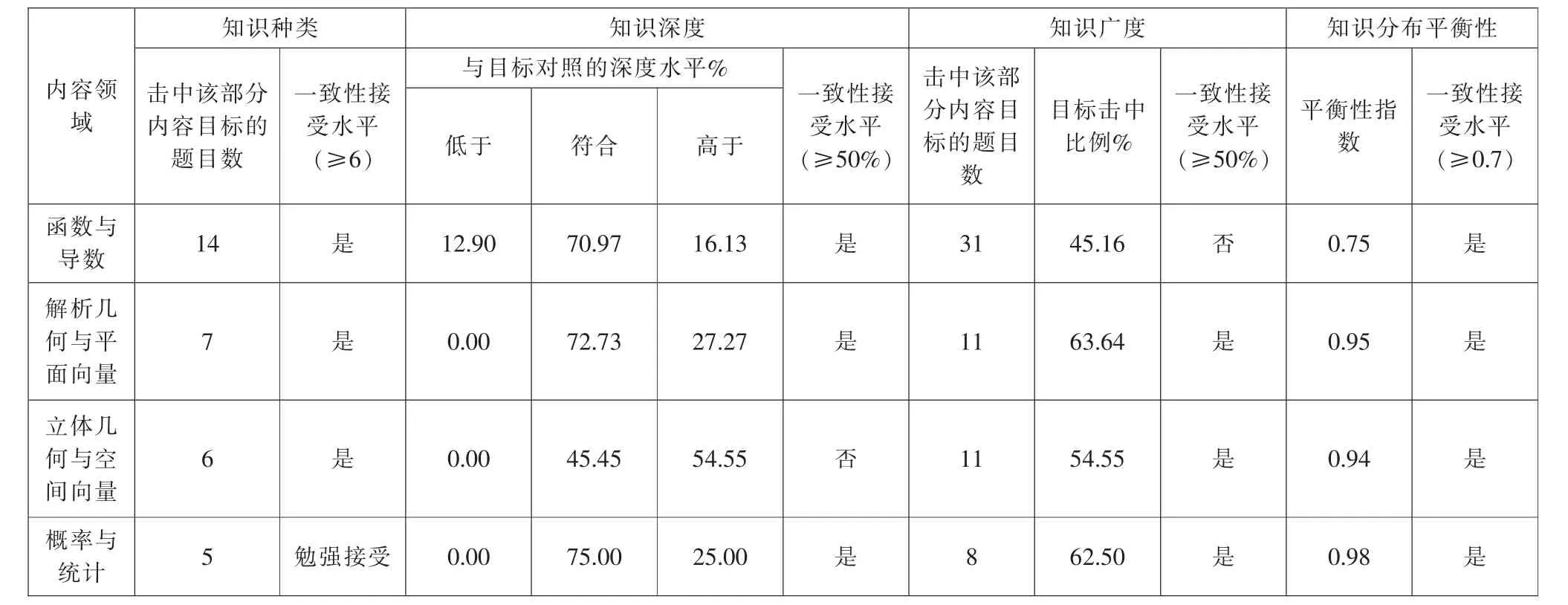
表3 基于Webb 模式的2020 年高考数学全国卷Ⅱ与课程标准的一致性分析

基于Webb 模式分析可知： 在知识种类这一维度，函数与导数、解析几何与平面向量、立体几何与空间向量主题考查的知识点均大于6， 达到一致性可接受水平，概率与统计主题包含5 道题目，勉强达到一致性接受水平；在知识深度这一维度；除立体几何与空间向量主题外， 其他主题均达到一致性可接受水平，高考试题中第20 题考查立体几何与空间向量的知识点，试题对学生的认知要求为“证明”，明显高于课程标准中“能”的认知水平，其次函数与导数、解析几何与平面向量、 概率与统计主题中考查的部分知识点水平高于课程标准的要求， 这是由于试题考查内容导致的，例如高考试题中第19 题对学生的认知要求明显高于“了解椭圆、抛物线的简单应用”；在知识广度这一维度，3 个主题均达到可接受水平，函数与导数主题中击中该部分内容的比例为45.16%，低于一致性接受水平；最后从知识的平衡性来看，4 个主题知识分布平衡与课程标准的一致性达到可接受水平， 但是函数与导数主题的平衡性指数较低， 函数是中学数学课程中最重要的学习内容之一，包含的知识点较多，考查点难以覆盖全面且分布均衡。

2. 基于SEC 模式的2020 年高考数学全国卷Ⅱ（理科）与课程标准的

首先需要确定对内容主题和认知水平的分类。由上文可知， 本研究中将内容主题按照课程标准分为4 个主题：函数与导数、解析几何与空间向量、立体几何与空间向量、概率与统计。其次是对认知水平的划分，本文只对知识技能进行分析，依据《义务教育课程标准（2011 年版）》中有关行为动词的分类，将认知水平分为：了解（知道、初步认识）、理解（认识、会）、掌握（能）、运用（证明）[18]这四类。

（1）基于SEC 模式的课程标准编码情况

根据本研究确定的内容主题以及认知水平的划分，将课程标准编码情况统计如表4 所示。

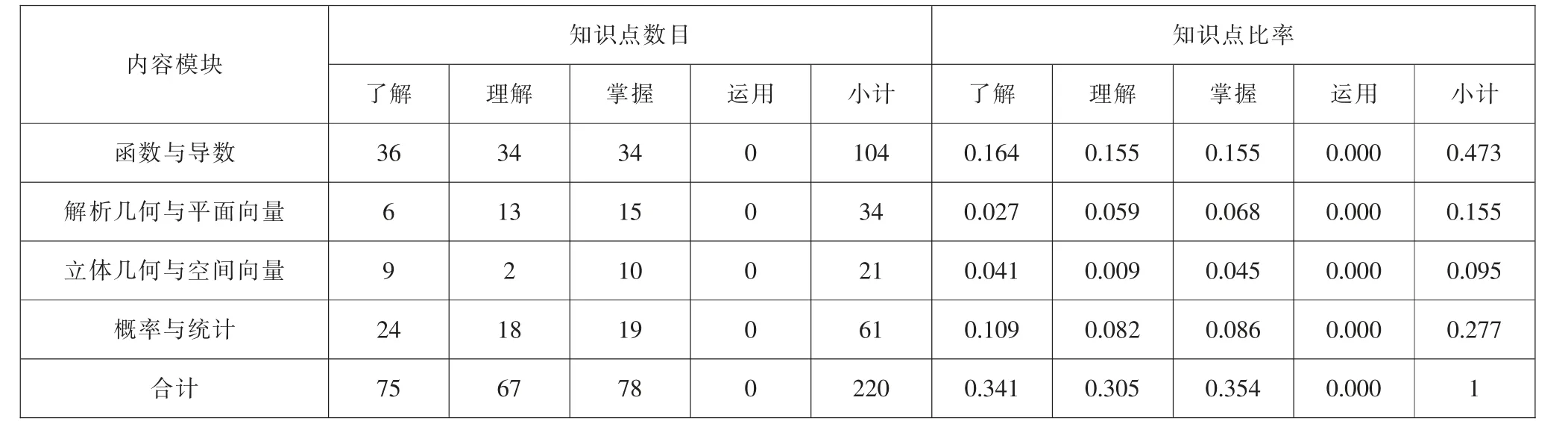
表4 课程标准中的知识点数目及比率表

（2）基于SEC 模式的2020 年高考数学全国卷Ⅱ编码情况

研究者对2020 年高考数学全国卷Ⅱ考查的内容进行分类整理， 统计出每个知识模块下对应各个认知水平考查内容的相应分值， 并呈现各知识点相应比率，如表5 所示。

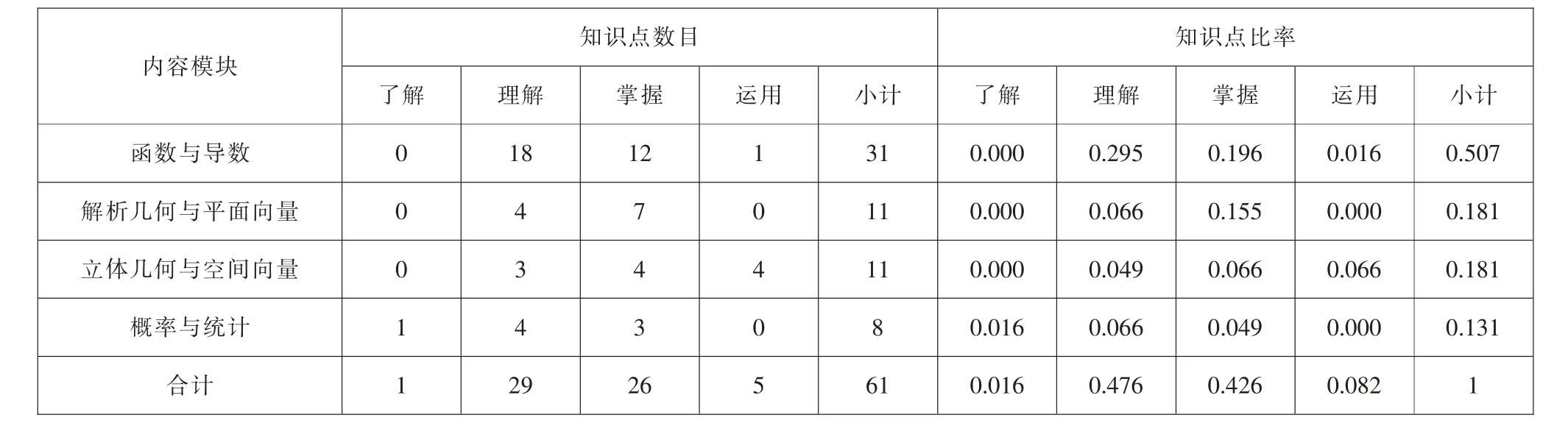
表5 2020 年高考数学全国卷Ⅱ的知识点数目及比率表

（3）基于SEC 模式的2020 年高考数学全国卷Ⅱ与课程标准的一致性结果

图1、图2 分别从内容主题和认知水平两个维度呈现2020 年高考数学全国卷Ⅱ与课程标准的一致性结果。

从图1 可以看出， 在内容主题维度， 函数与导数、 解析几何与平面向量这两个主题与课程标准基本保持一致， 而高考试题中立体几何与空间向量知识点占比约为18%， 比课程标准中知识点占比高出10%；课程标准中概率与统计知识点占比约为28%，比高考试题中知识点占比高出15%。 通过以上数据分析可以看出，2020 年高考数学全国卷Ⅱ（理科）在立体几何与空间向量、概率与统计这两大主题中，考查点与课程标准有较为明显的不一致， 对于立体几何与空间向量的考查要求明显高于课程标准的要求， 而对于概率与统计的考查要求明显低于课程标准的要求。 课程标准中对于概率与统计的内容要求中随机事件与概率、随机事件的独立性、统计图表等知识点均未在试题中体现， 这是由于高考试题各个内容主题的题目比例与课时比例相近， 概率与统计的课时比例较低，故考查内容不易过多。

从图4 可以看出，对于了解（知道/初步认识）认知维度，课程标准要求为0.34，高考试题为0.016，远低于课程标准要求；对于理解（认识/会）认知维度，课程标准要求为0.305，高考试题为0.476，明显高于课程标准要求；对于掌握（能）认知维度，课程标准要求为0.354， 高考试题为0.426， 略高于课程标准要求； 对于运用（证明） 认知维度， 课程标准要求为0.000，高考试题为0.082，高于课程标准要求。 这是由于部分题目的综合性较强，考查的知识点较多，提高了对学生的认知要求。

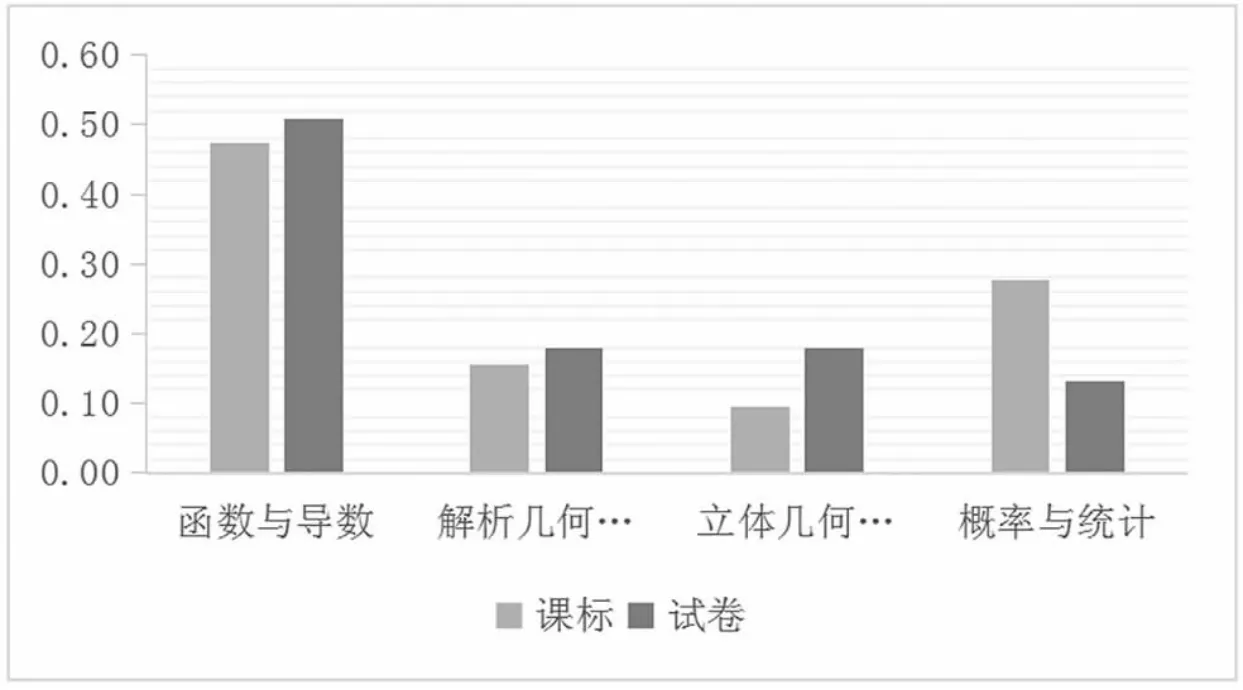
图1 试题与课程标准的内容主题比较

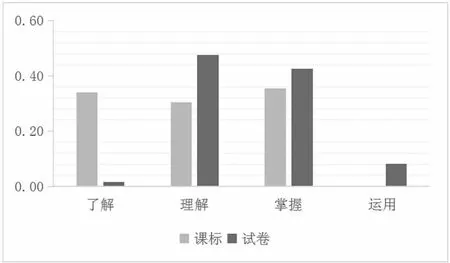
图2 试题与课程标准的认知水平比较

基于SEC 模式计算得出的一致性系数为0.602，可见2020 年高考数学全国卷Ⅱ试题与课程标准达到一定程度的一致，但未达到较高的一致性水平。

3. 基于Achieve 模式的2020 年高考数学全国卷Ⅱ（理科）与课程标准的一致性分析

由于SEC 模式中将认识水平划分为了解、理解、掌握、运用四个层次，了解与理解都是对学生认识水平较低的要求， 故在此处与Achieve 模式的挑战层次划分进行整合，将其作为层次1，掌握作为层次2，运用作为层次3。 基于Achieve 模式，从向心性、挑战性及均衡性三个维度展开2020 年高考数学全国卷Ⅱ与课程标准的一致性分析， 研究结果如表6、7 所示。

表6 向心性、挑战性分析结果

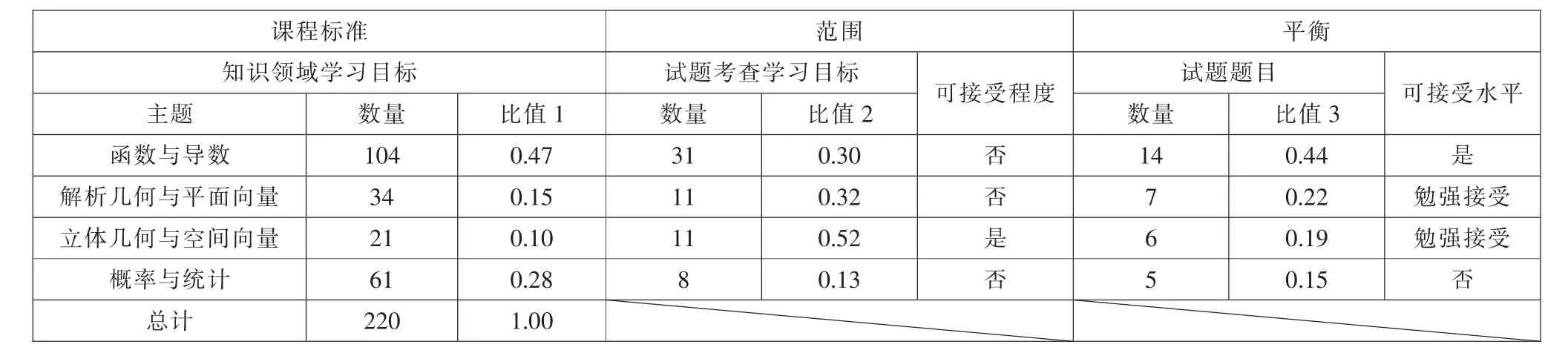
表7 均衡性分析结果

2020 年高考理科数学全国卷Ⅱ在内容向心性方面，84%的试题达到“完全一致”水平，6%的试题达到“部分一致”水平，1%的试题与新课标为“完全不一致”水平。高考试题第21 题第（3）问应用第（2）问“利用导数研究函数的最大值”得到的结论进行迁移，证明给定的代数式之间的大小关系这一内容未出现在课程标准的考查要求中。 在表现向心性方面，66%的试题达到“完全一致”水平，13%的试题达到“部分一致” 水平，21%的试题与新课标为 “完全不一致”水平。在挑战性来源维度，试题无描述、图表等错误；在挑战层次维度， 高考试题兼顾不同难度知识点的考查，重视学生对知识点的掌握情况，同时有31%的试题考查学生的高层次能力。 在范围方面， 函数与导数、解析几何与平面向量、概率与统计未达到满意程度， 说明试题涵盖的知识点与课程标准内容要求相比考查率较低。 在平衡方面，除概率与统计外，其他主题涉及的试题平衡指数较高。

四、研究启示与反思

综上所述， 运用Webb、SEC、Achieve 一致性分析模式对试题与课程标准编码， 进而提出以下几点启示与思考：

（1）三种一致性分析模式相互联系，研究结果是互补的。 研究发现：2020 年高考数学全国卷Ⅱ（理科）与课程标准达到一定程度的一致，但部分维度未达到较好的一致性水平。 如SEC、Achieve 模式均发现： 概率与统计主题试题涵盖的知识点与课程标准内容要求相比考查率较低。 Webb、Achieve 模式发现： 函数与导数试题考查点与课程标准中相应主题的内容要求一致性较低。

（2）三种一致性分析模式具有各自的优势。在编码过程中，Webb 模式分析质效高， 仅用一张表格就清晰呈现高考试题与课程标准在各维度的一致性程度；SEC 模式操作简便， 该模式的重心是从内容主题、 认知水平两个维度构造课程标准与高考试题的二维矩阵编码， 进而应用条形统计图呈现两者在内容主题、认知水平的差异；而Achieve 模式涉及较多对试题的定性内容的分析， 不仅包含对试题涉及的知识点、考查的认知水平的分析，还涉及对试题的科学性、操作过程的分析。

（3）主题分类的合理性在一致性研究中尤为重要，由于高中课程内容包含必修课程、 选择性必修课程与选修课程， 本研究在参考初中数学课程内容数与代数、图形与几何、概率与统计的划分及其他研究者的分类（1.三角函数与数列、不等式与向量两个主题的划分差异较大[19][20]，2.根据数学课程内容[21]，3.根据数学教材的内容安排[22]）基础上，对高中数学内容进行了细致分析， 将高中课程内容划分为：“函数与导数”、“解析几何与平面向量”、“立体几何与空间向量”、“概率与统计”四个主题。

本文聚焦了试题对学生的必备知识与认知水平的要求，而如何从教育部考试中心研制的《中国高考评价体系》四层“核心价值、学科素养、关键能力、必备知识”角度开发、构建更合理的、完善的一致性分析模式，丰富和完善我国的高考评价体系，也是广大教育研究者日后研究的方向。