二阶混合有限体积法求解Navier-Stokes 方程的稳定性及误差估计

张杰华, 韩明华

(凯里学院理学院，贵州 凯里 556011)

1 引言

Navier-Stokes(N-S)方程是计算流体力学(CFD)中的基本方程，而局部守恒性是CFD 数值方法发展的一个重要准则.有限体积法(FVM)最大的特点就是能在其控制体积上保持某种物理量的局部守恒，同时继承了有限元法和有限差分法的优点，因此FVM 已成为解决CFD 问题的一种流行数值方法.

近年来FVM 的研究非常活跃.文献[1,2]分析和构造了一类椭圆问题的二阶和三阶FVM.它们根据三角网格上的某些几何要求，建立了离散双线性型一致局部椭圆性的充要条件，为研究各类高阶FVM 方程的稳定性提供了一种通用的方法.文献[3]利用两套网格—速度场的粗网格和压力场的细网格，在三角形网格上建立了求解N-S 方程的一阶FVM，并证明了其稳定性.文献[4]利用增加稳定项的方法使其N-S 方程对应的一阶FVM 方程满足稳定性，从而得到三角形网格上的最优误差估计.另外还有许多其它关于研究FVM 求解N-S 方程稳定性理论的工作，如文献[5–13]及其参考文献.然而，这些工作大多是局限于在三角形网格上采用分片线性多项式函数逼近速度场的低阶FVM，其主要思想是利用增加稳定项的技术使N-S 方程的一阶FVM 方程满足稳定性条件.这在一定程度上导致了求解FVM 方程的计算量增大及其稳定性理论分析的难度，并且其理论结果只有关于速度项的一阶H1模误差估计.到目前为止，很少出现利用二次多项式函数逼近N-S 方程速度场的高阶FVM 的相关理论研究工作.

本文考虑利用二阶混合FVM 求解定常N-S 方程，即对速度场的试验函数空间取为分层二次多项式函数的有限元空间，检验函数空间由对偶剖分网格上的特征函数及二次多项式函数所组成，压力场的试验函数空间和检验函数空间均取为线性有限元空间.利用二阶混合FVM 的离散双线性型与其对应的有限元法离散双线性型之间的等价关系，本文证明了求解N-S 方程二阶混合FVM 的稳定性，进而得到了二阶混合FVM 关于速度项和压力项的最优误差估计收敛阶.

本文有如下几个特点.首先，本文构建的混合FVM 的对偶剖分网格与线性FVM 的相同，从而其理论分析与其技术的实现都较一般传统FVM 简单.另外，本文不用增加稳定项，不需要粗细两套三角形网格，即可得到求解N-S 方程的二阶混合FVM 的稳定性及其最优误差估计.其次，对于N-S 方程中的非线性项，本文直接在FVM 的控制体积上对其进行离散化，从而利用其FVM 的非线性项与其对应的有限元法的非线性项之间的关系，使得二阶FVM 的理论分析及其计算技术的实现更加方便.此外，本文首次证明了二阶FVM 求解N-S 方程关于速度场的H1模和压力场的L2模的最优误差估计.不仅本文的理论结果与其对应的有限元法结论相同，而且其证明方法具有一般性，可被应用于更一般的高阶及高维有限体积法理论分析的情形.

第2 节将介绍一些相关记号和N-S 方程的变分问题.第3 节建立求解N-S 方程的二阶混合FVM.第4 节将证明此二阶FVM 的稳定性及其该方法的最优阶误差估计.第5 节将给出数值算例来验证本文结论的正确性.

2 Navier-Stokes 方程

记Ω 为R2中的一个多边形区域，∂Ω 为其边界，设

并用//·//0表示L2(Ω)空间的范数，用|·|m和//·//m分别表示Hm(Ω)空间的半范数和全范数.设C,c(或含下标)表示一类与网格尺寸无关的正常数，与文中出现的(µ,Ω,f)有关.

本文考虑如下定常N-S 方程：求u := (u1,u2)∈(Ω)∩H2(Ω)和p ∈(Ω)∩H1(Ω)满足

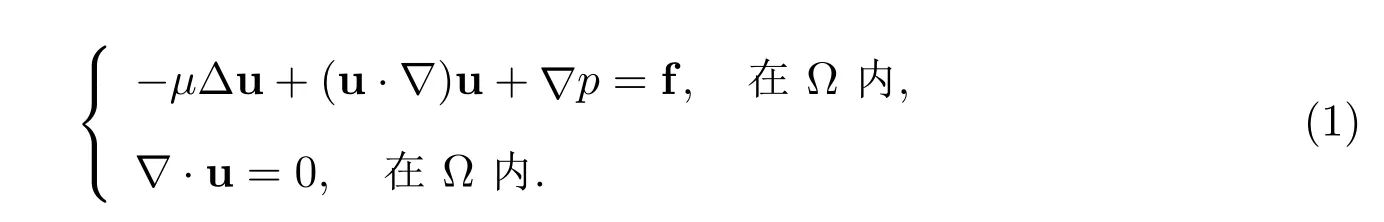
此处，f := (f1,f2)为作用于流体上的外力，µ> 0 为流体粘度，u 为所求速度场，p为所求压力场.

方程(1)的变分形式为：求u∈(Ω)∩H2(Ω), p ∈(Ω)∩H1(Ω)满足

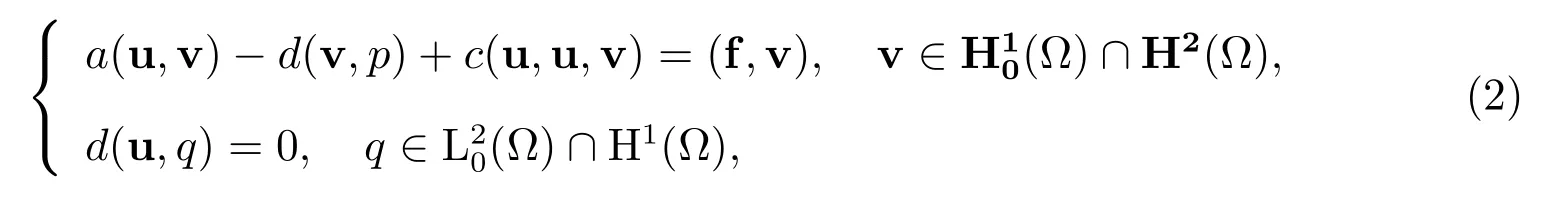
此处

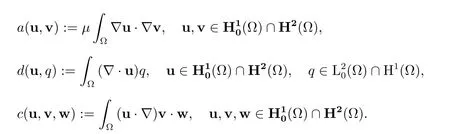
利用Green 公式和方程(1)的第二式及其边界条件可知，对任意的u,v,w∈(Ω)∩H2(Ω)，三线性型c(·,·,·)满足

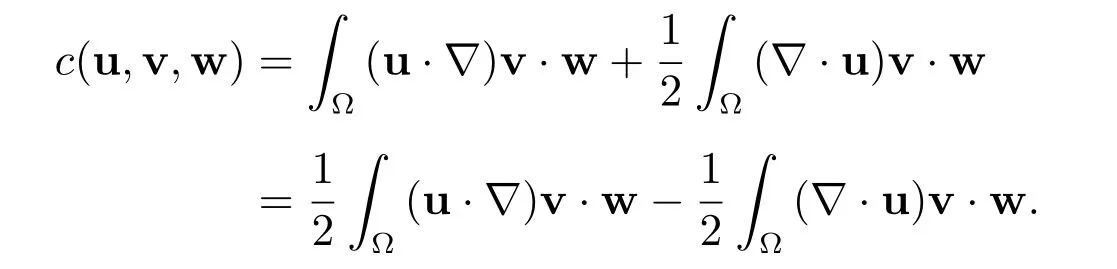
另外，对任意的u,v,w∈(Ω)∩H2(Ω)，三线性型c(·,·,·)还满足[14,15]

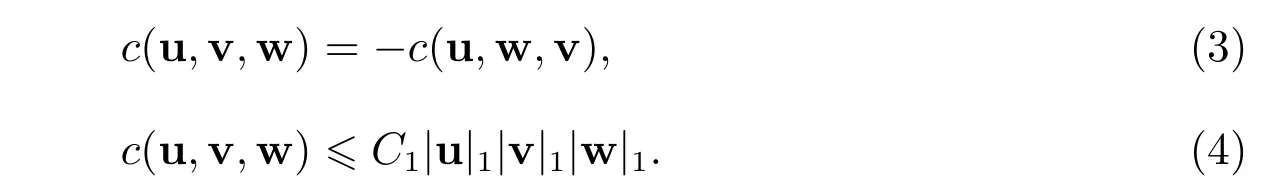
本文假设原方程(1)总存在唯一解，即µ与f 满足如下条件[15]

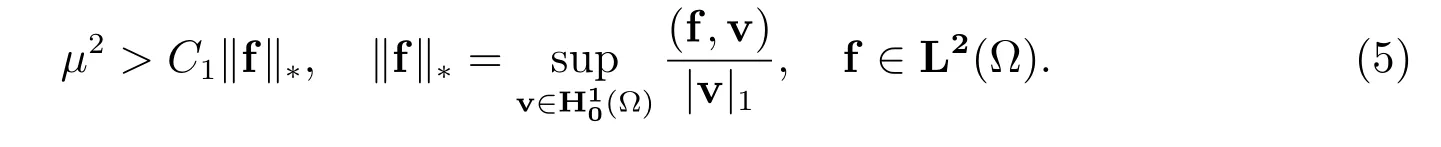
3 有限体积法

本节将建立求解N-S 方程(1)的二阶混合FVM 方程.下面依次介绍FVM 的三角形网格剖分及其试验函数空间，对偶网格剖分及其检验函数空间，最后给出求解N-S 方程(1)的FVM 方程.

设T:={K}为Ω 上的拟一致三角形网格剖分[16,17]，即存在一个与网格尺寸h

无关的正常数θinf，使得三角形单元K ∈T的最小内角θmin,K满足θmin,Kθinf，且存在常数γ> 0，对所有的K ∈T满足γh2meas(K)h2.记T:={T}为Ω 上的拟一致三角形剖分族.设取N-S 方程(1)中的速度场与压力场的试验函数空间分别为如下的有限元函数空间

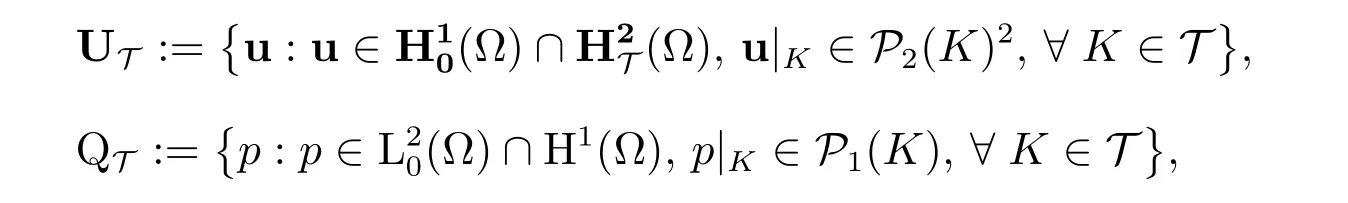
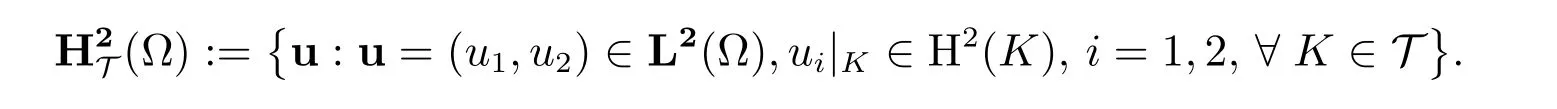
其中Pr(D)表示在区域D上的r次多项式函数空间.具体地，取速度场的试验函数空间UT为[1,2,18]

UT=V1,T ⊕W2,T,

此处

V1,T:=span{ϕP:P ∈N},W2,T:=span{ϕPϕP′:P,P′∈N}.

记N表示剖分T={K}的内部节点的集合，则ϕP表示在节点P ∈N处的线性插值基函数，即ϕP ∈P1(K)，且若P=P′，则ϕP(P′)=1，若P ̸=P′，则ϕP(P′)=0.压力场的试验函数空间及检验函数空间均取为QT，其基函数集为

ΨT:={ϕP:P ∈N}.

下面介绍二阶混合FVM 的对偶剖分及其关于速度项的检验函数空间[1,2,18].分别用直线连结三角形的重心与各边的中点，则将每个三角形K ∈T分解成三个区域.把包含三角形顶点的多边形区域称之为一个控制体积K∗，则所有的这些控制体积K∗就形成了区域Ω 的一个对偶剖分T ∗，即T ∗:={K∗}.显然，二阶混合FVM 的对偶剖分与线性FVM 的相同，因此其理论分析较传统Lagrange 二阶有限体积法简单.取速度场的检验函数空间为UT ∗满足

UT ∗=V0,T ∗⊕W2,T,

这里V0,T ∗:= span{χP:P ∈N}为控制体积K∗上的分片常数函数空间，χP为其顶点P ∈N处的控制体积的特征函数.显然dimUT=dimUT ∗.下面引入从UT到UT ∗的一个线性映射.对任意的

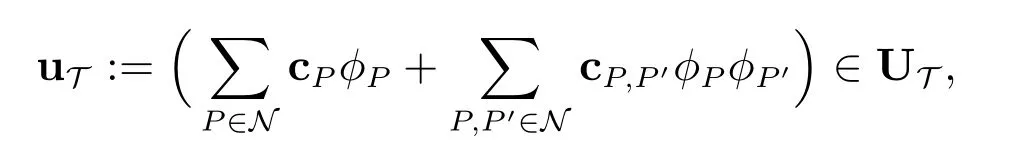
设ΠT ∗:UT →UT ∗满足

这里cP,cP,P′为向量常数.

利用从UT到UT ∗的线性映射ΠT ∗，建立如下求解N-S 方程(1)的FVM 方程：求(u,p)∈(UT,QT)，使得对所有的(v,q)∈(UT,QT)满足

这里

其中n 为∂K∗上的单位外法向量.此处的非线性项cT(u,w,ΠT ∗v),u,w,v∈UT，是利用方程(1)的第一式加上连续性方程后在每个控制体积K∗∈T ∗上进行积分求和而得到.特别地，若用v∈UT代替非线性项cT(u,w,ΠT ∗v)中的ΠT ∗v∈UT ∗，则有

cT(u,w,v)=c(u,w,v), ∀u,w,v∈UT.

因此利用非线性项cT(u,w,ΠT ∗v)与c(u,w,v)的关系，可以简化FVM(6)的理论分析.

方程(6)即为本文所分析的FVM 方程.注意到UT ∗包含控制体积上的特征函数，因此FVM(6)关于速度项的数值解具有局部守恒性.

4 稳定性及误差估计分析

本节主要分析FVM(6)在三角形网格上的稳定性及其误差估计.注意到FVM(6)中含压力项的离散双线性型与其对应的有限元法离散双线性型具有等价的关系，以及FVM(6)的椭圆双线性型满足强制性，从而在粘度µ和外力f 满足一定的条件下(与有限元法类似)，利用Brouwers 不动点定理，可以得到FVM(6)的稳定性及其方程解的唯一性.一旦FVM(6)的稳定性成立，即可推出其关于速度场的H1(Ω)模与压强场的L2(Ω)模的最优误差估计.

首先，我们引入一些结论.关于线性映射ΠT ∗: UT →UT ∗，由文献[18,19]可知如下性质成立.

引理1对任意的u∈UT，有

若T为拟一致剖分，则对任意的u∈UT，有

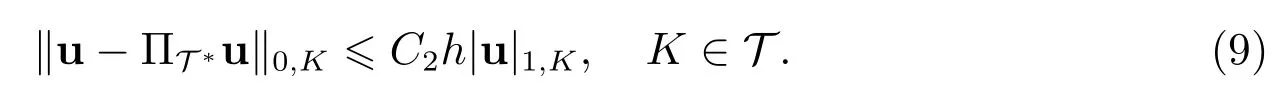
由文献[14]可知，对任意的(v,q)∈(UT,QT)，双线性型dT(v,q)具有如下估计.

引理2若T为拟一致剖分，则对任意的(v,q)∈(UT,QT), T ∈T，存在常数C，使得

|dT(v,q)|C|v|1//q//0.

另外，对任意的q ∈QT，存在常数c满足

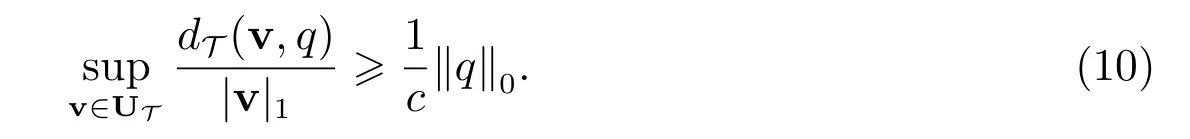
结合引理1、引理2，由文献[19]可知：

引理3对任意的(v,q)∈(UT,QT)，有

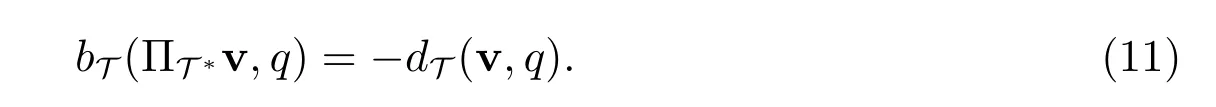
结合不等式(10)，则对任意的q ∈QT，存在常数c满足

引理4若T为拟一致剖分，则对所有的(v,p)∈(UT,L20(Ω)∩H1(Ω)), T ∈T，存在常数C满足

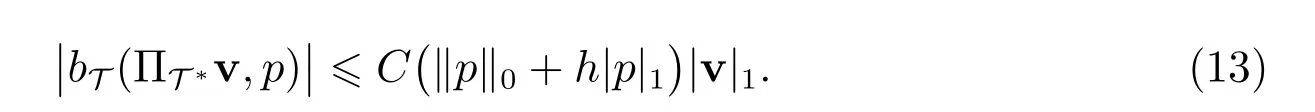
引理5若T为拟一致剖分，θmin,K> 14.18◦, K ∈T，则对所有的u∈(Ω)∩(Ω),v∈UT, T ∈T，存在常数C, c4满足

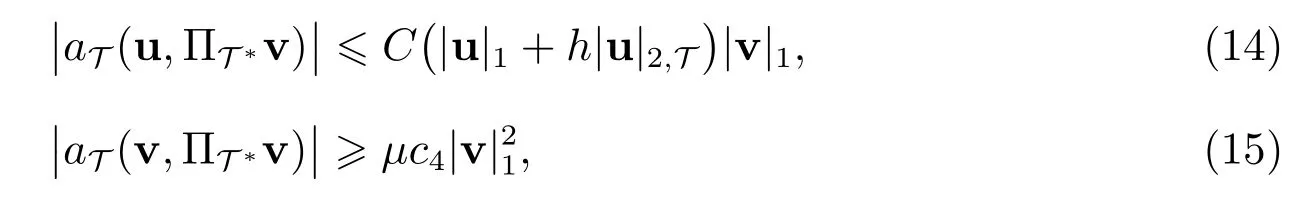
这里

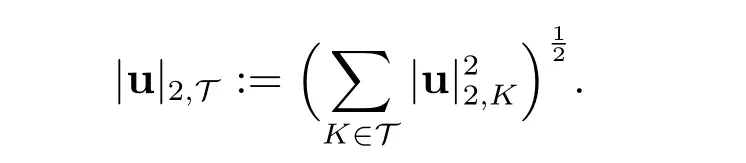
记C(·,·)为空间(UT,QT)×(UT,QT)上的双线性型泛函，即令

C((u,p),(v,q)):=aT(u,ΠT ∗v)+bT(ΠT ∗v,p)+dT(u,q).

类似于文献[19]中Theorem 7 的证明，利用引理2、引理4、引理5 及Babuska-Lax-Milgram 定理[20]，可得如下估计.

引理6若T为拟一致剖分，θmin,K>14.18◦, K ∈T，则对所有(u,p)∈(UT,QT),T ∈T，存在常数C, c5满足

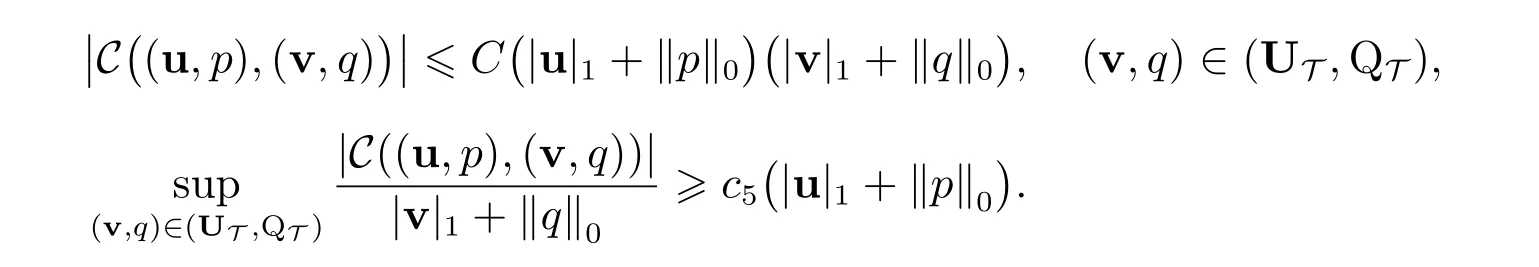
有了上述准备，下面证明FVM(6)的稳定性及解的唯一性.记//·//m,p为Soblev 空间Wm,p(Ω)的范数，如下结论将会被用到.

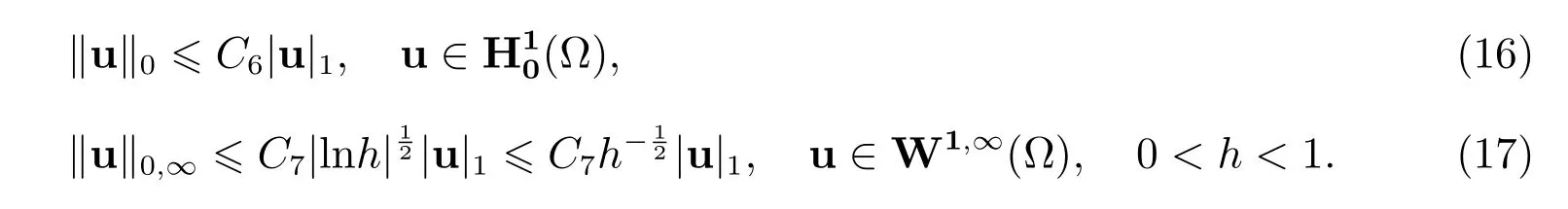
定理1若T为拟一致剖分，θmin,K>14.18◦, K ∈T，且对所有的h>0 满足

此处

则FVM(6)至少存在一组解(u,p)∈(UT,QT).如果µ>0,f∈L2(Ω), h>0，且满足

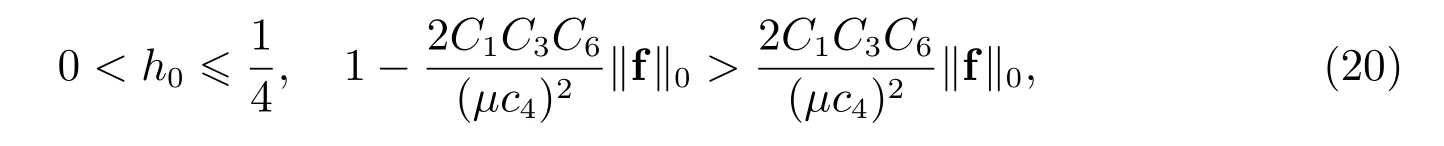
则FVM(6)存在唯一解，且满足

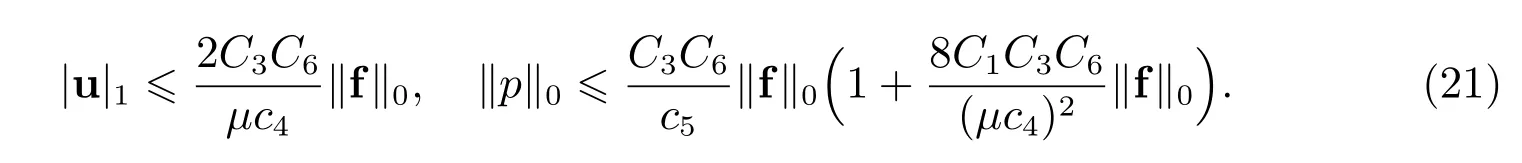
证明 这里主要利用Brouwers 不动点定理[21]证明结论.记

对任意的(v,q)∈(UT,QT)，设映射PT:(UT,QT)→(UT,QT)满足

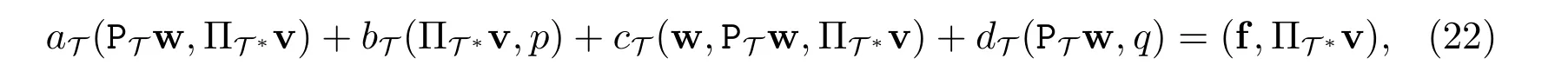
此处PT(w,p):=(PTw,p)=(u,p)∈(UT,QT)以及(w,·)∈BM.

先证FVM(6)解的存在性，即证PT(BM)⊂BM.首先考虑|u|1的估计.在等式(22)中取(v,q)=(u,p)∈(UT,QT)，则有

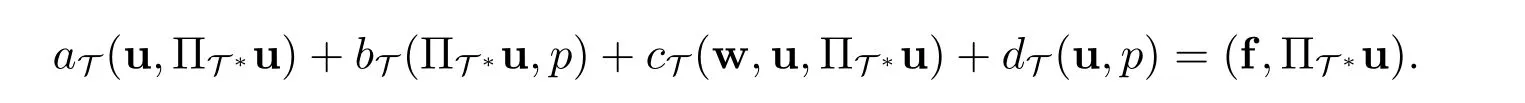
利用引理3 中的等式(11)，则上式可简化为

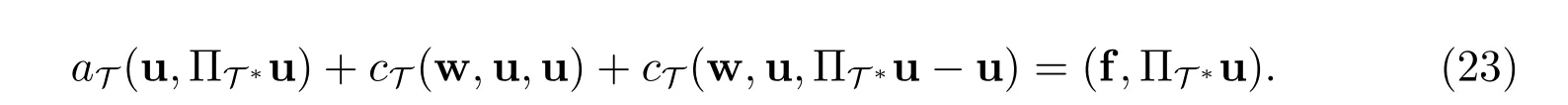
下面考虑等式(23)中的每一项.对于第一项，由估计(15)可知，对任意的u∈UT，有

对于第二项，由cT(·,·,·)的定义及关系式(3)可知，对任意的w,u,v∈UT，有

下面估计等式(23)左边的第三项.注意到u∈UT ⊂W1,∞(Ω)，利用Cauchy-Schwartz 不等式及估计(9)式和(17)式，则可得

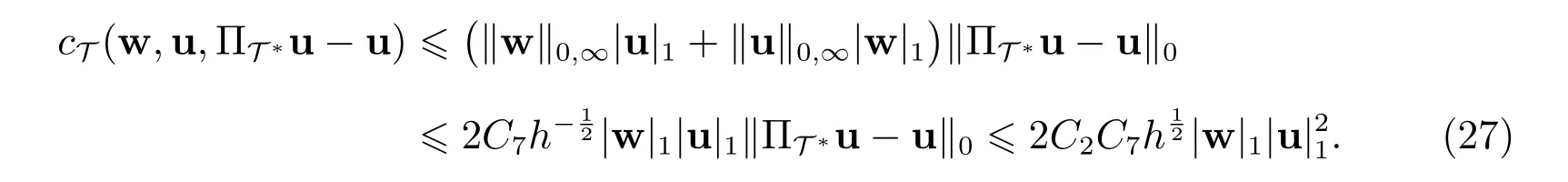
注意到(w,·)∈BM，即

因此利用不等式(28)和条件(19)式，可将估计(27)式化为

对于等式(23)的右端项，利用Cauchy-Schwartz 不等式及范数估计(8),(16)可得

从而将上述关系式(24),(26),(29),(30)分别代入等式(23)，整理可得

再结合条件(18)式，因此有

下面考虑//p//0的估计.利用上述类似的方法，注意到w,u,v∈UT，则由估计(25),(27)及关系式(4)可得

取

则由估计(32), (33)及(28)可得

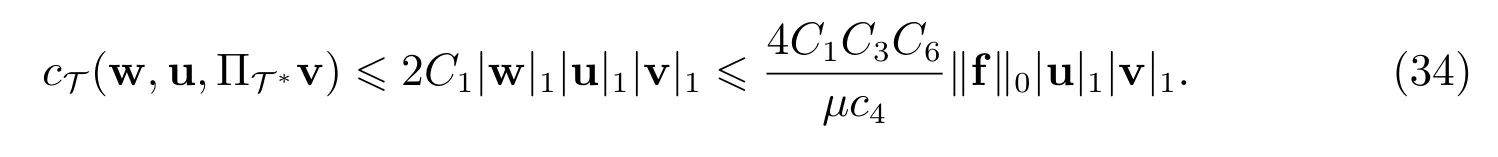
另外，由引理6 中的第二个不等式，结合等式(22)，可知对任意的(u,p)∈(UT,QT)有

将估计(30),(34)代入上式可知，对任意的p ∈QT，有

结合估计(31)可得

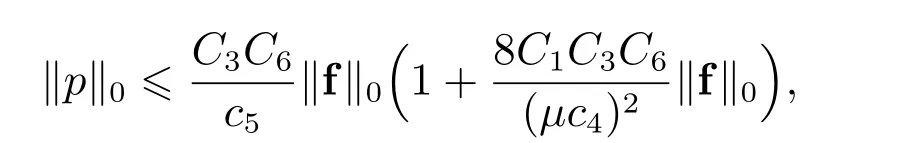
从而PT(BM)⊂BM.因此由Brouwers 不动点定理可知FVM(6)至少存在一组解.

下面证明FVM(6)解的唯一性.设(u,p)∈(UT,QT)和(¯u,¯p)∈(UT,QT)为FVM(6)的两组解，即对任意的(v,q)∈(UT,QT)，有

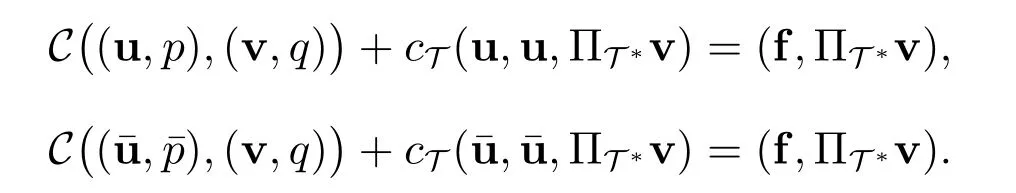
易知u,均满足估计(31).利用上面两式作差可得

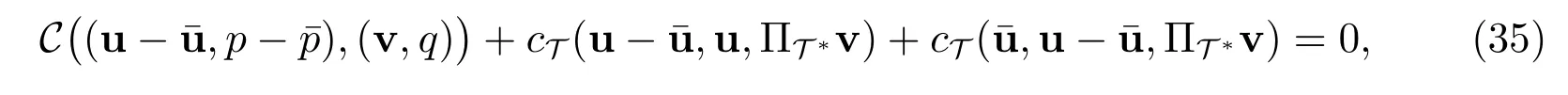
这里用到了

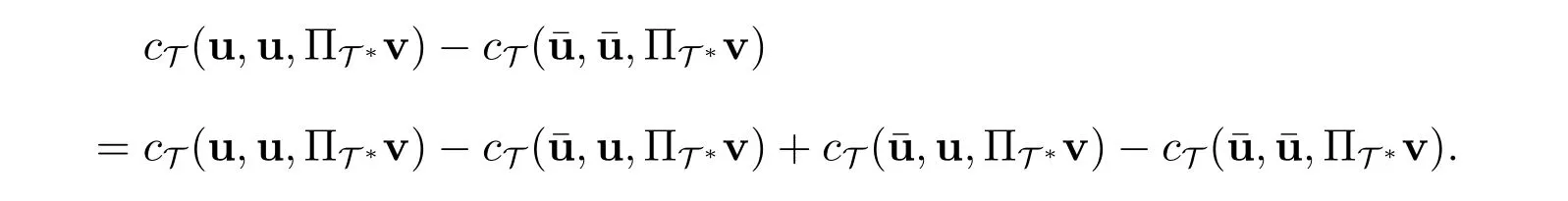
设(v,q) = (u−,p −¯p) := (e,η)∈(UT,QT)，则由估计(24)的结论可知，等式(35)左端第一项满足

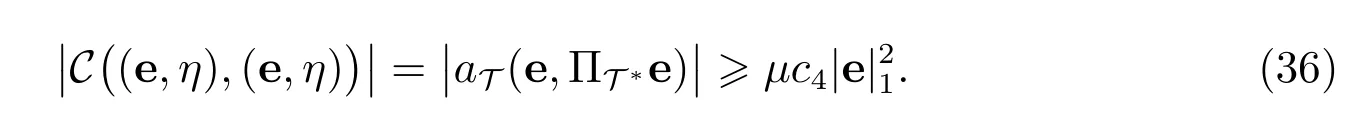
另外，由关系式(25)和(26)可知，等式(35)左端第二与第三项之和满足

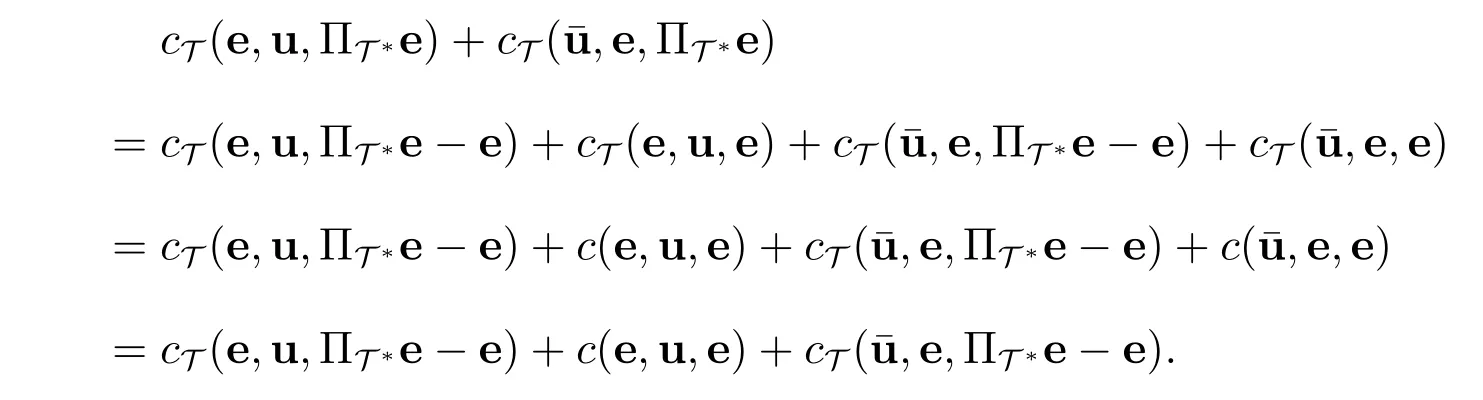
上式结合估计(27)和(4)得

再由估计(31)和条件(19)可知，等式(35)左端第二与第三项之和满足

利用估计(36)和(38)，整理等式(35)，可得

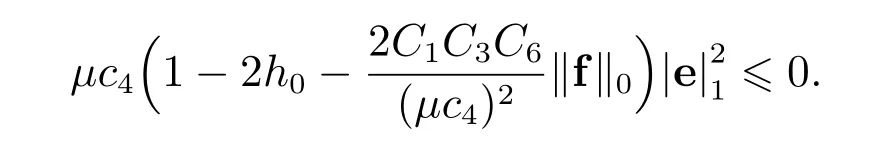
再由条件(20)的第二式可得

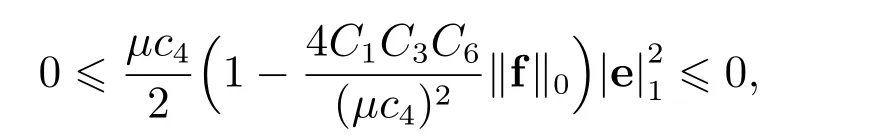
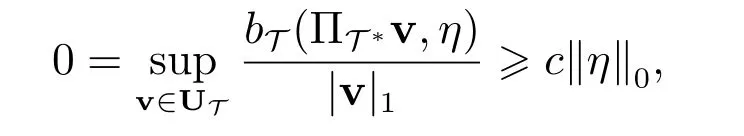
因此p=.

综上所述，FVM(6)在条件(20)下存在唯一解.

此定理说明，当网格尺寸h加密到一定的粗细时，即条件(18)成立时，FVM(6)存在数值解.若µ与f 满足条件(20)的第二式，则当网格尺寸h进一步加密时，FVM(6)具有唯一解.结合假设条件(5)与条件(20)可知，在原问题(1)存在唯一解的条件下，要使FVM(6)也有唯一解，那么µ与f 须满足

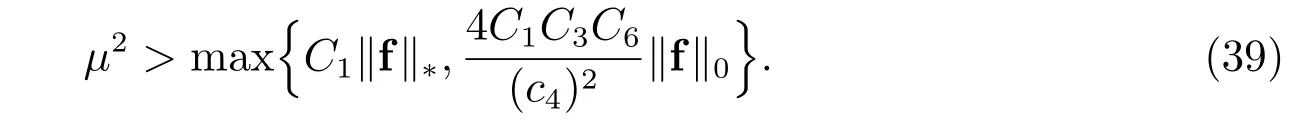
注意到由//f//∗的定义及范数估计(16)可知

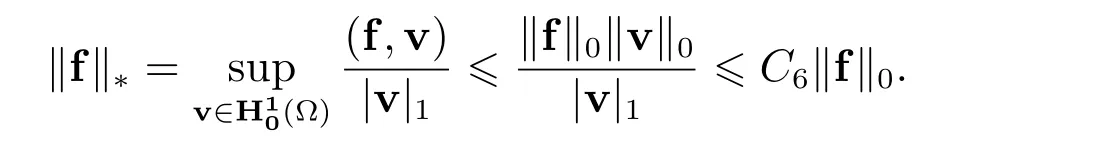
一般地可取4C3> 2c4(c4)2，从而可知当µ与f 满足条件(20)时，条件(39)一定成立.即，在FVM(6)存在唯一解的条件下，原问题(1)也一定有解.

有了FVM(6)的稳定性，下面将考虑FVM(6)关于速度场的H1(Ω)模与压强场的L2(Ω)模的误差估计.为此，需要一个强于(20)的假设条件

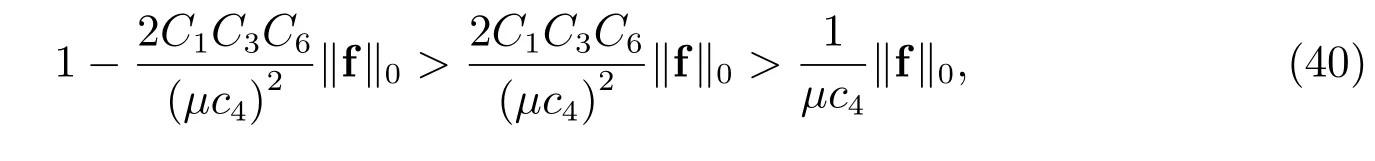
其中f∈L2(Ω).即要求µ与f 满足

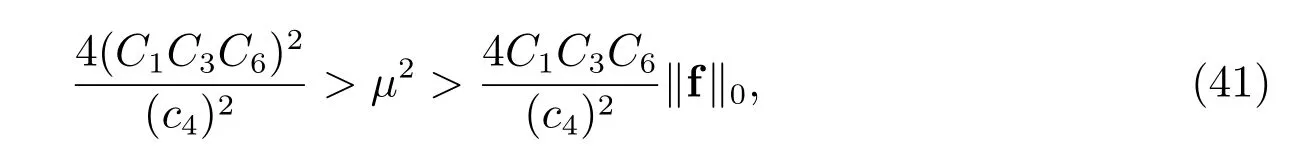
这里仍取4C3> 2c4(c4)2.从而利用上述FVM(6)的稳定性结及插值误差估计，可得如下定理.

定理2设(u,p)∈((Ω)∩H3(Ω),(Ω)∩H2(Ω))为原方程(1)的真解，(uT,pT)∈(UT,QT)为FVM(6)的数值解.若T为拟一致剖分，θmin,K> 14.18◦, K ∈T，则当h> 0 满足条件(18)，且f∈L2(Ω)和µ> 0 满足(40)时，存在常数C使得对所有的T ∈T，有

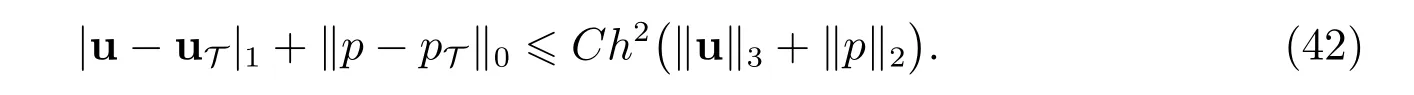
为了证明定理2，下面首先介绍两个引理.

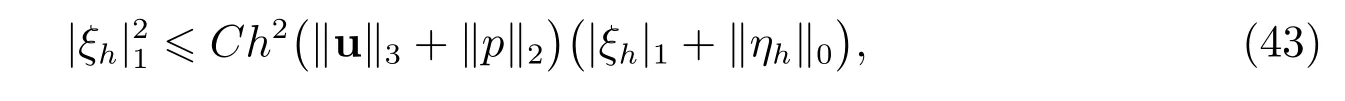
引理7如果定理2 的所有条件成立，则存在常数C满足这里ξh:=uT −u∈UT, ηh:=pT −p ∈QT，其中,为插值算子.

证明 此引理的证明主要利用离散双线性型aT(·,ΠT ∗·)的连续性和椭圆性，离散双线性型bT(ΠT ∗·,·)的连续性，另外还用到插值误差估计.

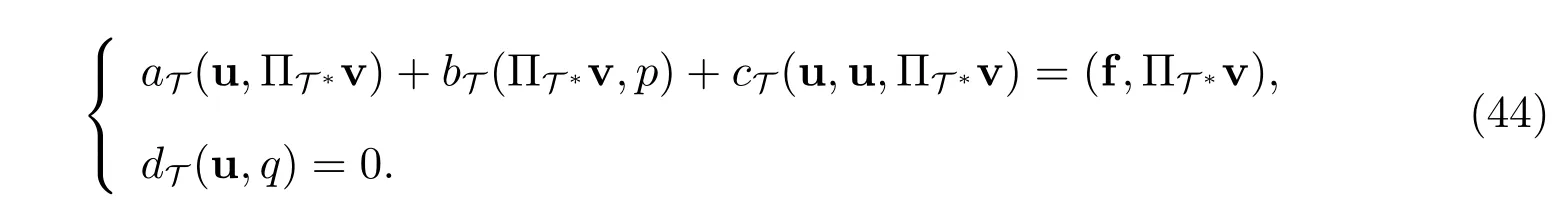
在FVM(6)中令(u,p):=(uT,pT)∈(UT,QT)，则有

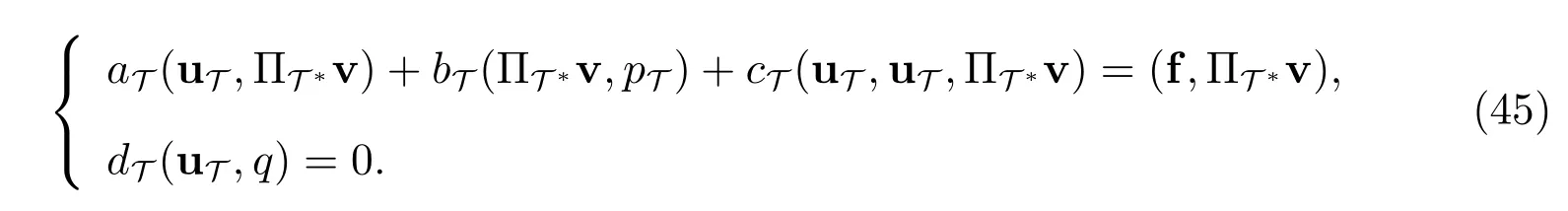
利用(44)式减去(45)式，可得

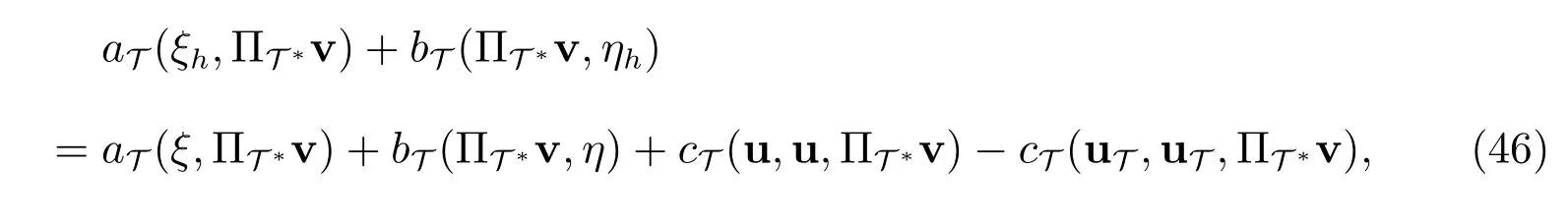
及

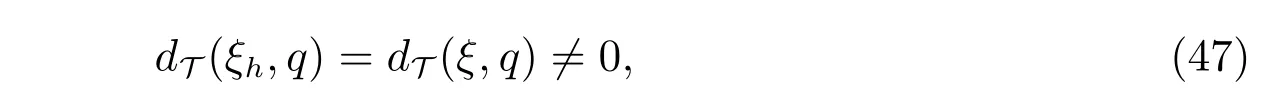
这里ξ:=u−u∈(Ω)∩H2(Ω), η:=p −p ∈(Ω)∩H1(Ω).

在等式(46)中取v=ξh ∈UT，在等式(47)中取q=ηh ∈QT，则由等式(11)可知

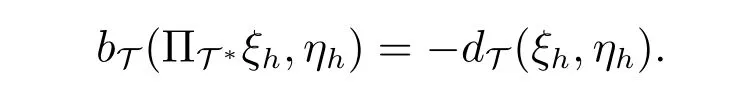
因此由等式(46)和(47)，可得

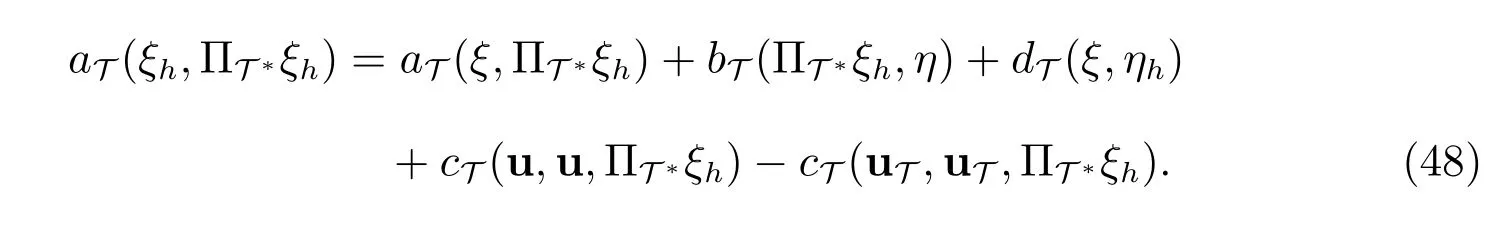
注意到上式的最后两项可展开为

再将其回代到等式(48)中可得

下面考虑等式(49)右端的每一项估计.首先，注意到ξ ∈∩H2⊂∩，因此由估计(14)及插值误差估计可知，对任意的ξ ∈(Ω)∩H2(Ω), ξh ∈UT，有

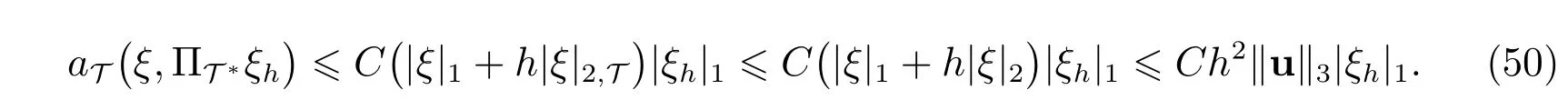
再由估计(13)及插值误差估计可知，对任意的ξh ∈UT, η ∈(Ω)∩H1(Ω)，有

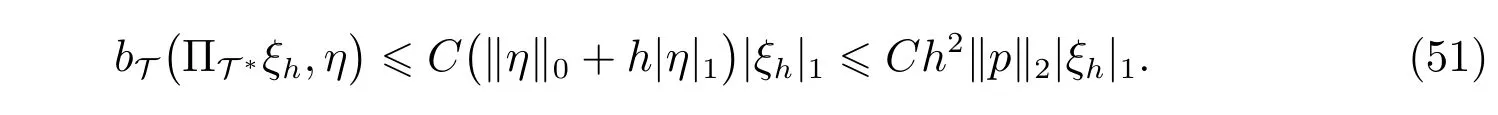
利用Cauchy-Schwartz 不等式及插值误差估计，可知对任意的ξ ∈(Ω)∩H2(Ω), ηh ∈QT，有

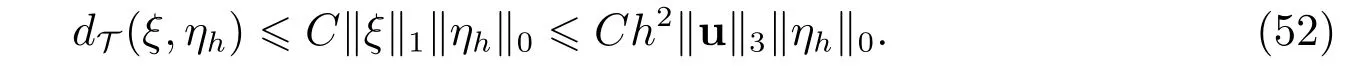
下面考虑等式(49)右端的第三项估计.利用估计(32)和(33)可知，等式(49)右端的第三项满足

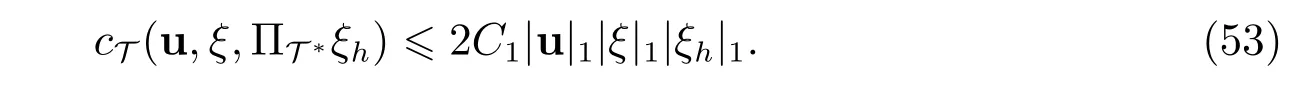
因为u∈(Ω)∩H3(Ω)为方程(1)的解，因此必满足变分方程(2).在方程(2)中取(v,q):=(u,p)∈((Ω)∩H2(Ω),(Ω)∩H1(Ω))，并利用范数估计(16)可知

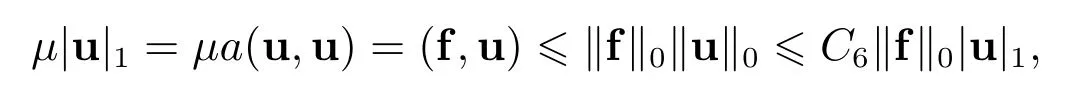
即

其中f∈L2(Ω).结合估计(53)和(54)，利用插值误差估计可得

下面考虑等式(49)右端的第四项的估计.事实上，利用估计(21)的结论

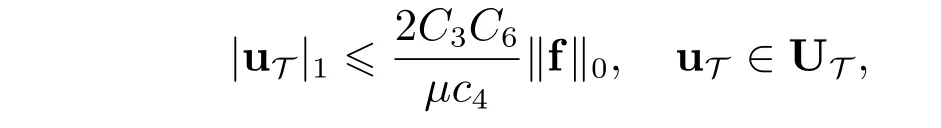
及插值误差估计，等式(49)右边的第四项满足如下估计

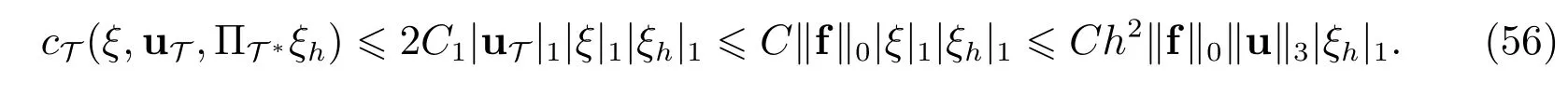
因此将估计(50),(51),(52),(55),(56)代入等式(49)右端，可得

接下来考虑等式(49)左端项的估计.类似于不等式(37)的推导，可得

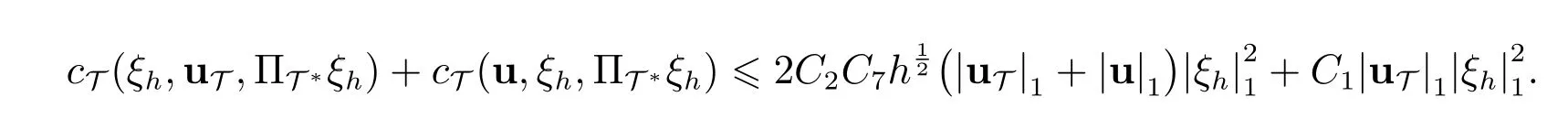
这里

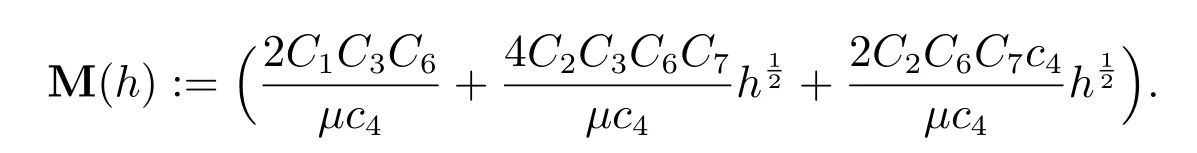
注意到c42C3，利用条件(18)和(19)，则由不等式(58)可得

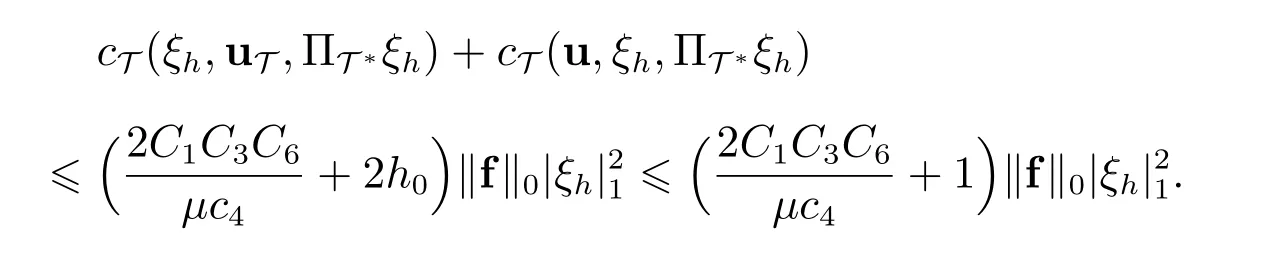
因此，结合估计(15)的结论，可知等式(49)的左端满足如下估计

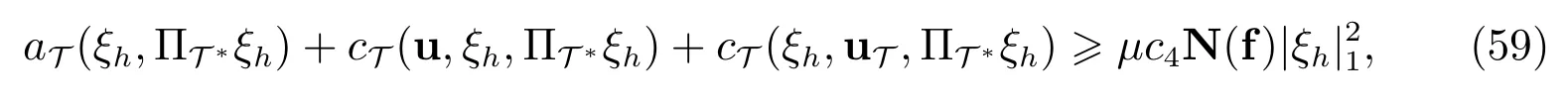
其中

考虑到条件(20)和(40)，可知N(f)>0.因此由不等式(59)可得

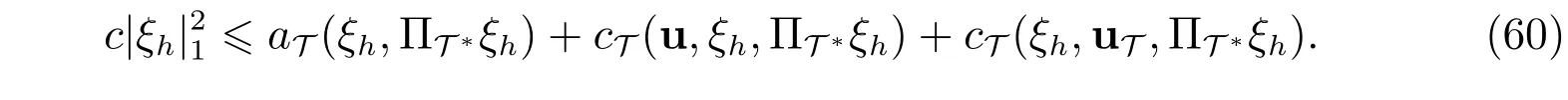
再结合估计(57)和(60)，可得

即证结论(43).

引理8如果定理2 的所有条件成立，则存在常数C满足

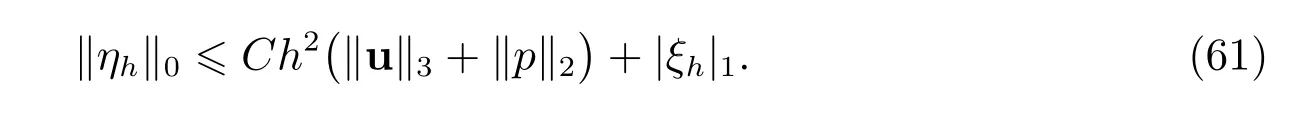
证明 此结论的证明利用双线性型bT(ΠT ∗·,·)的inf-sup 条件，双线性型aT(·,ΠT ∗·)的连续性，以及插值误差估计.

首先，由等式(46)可知

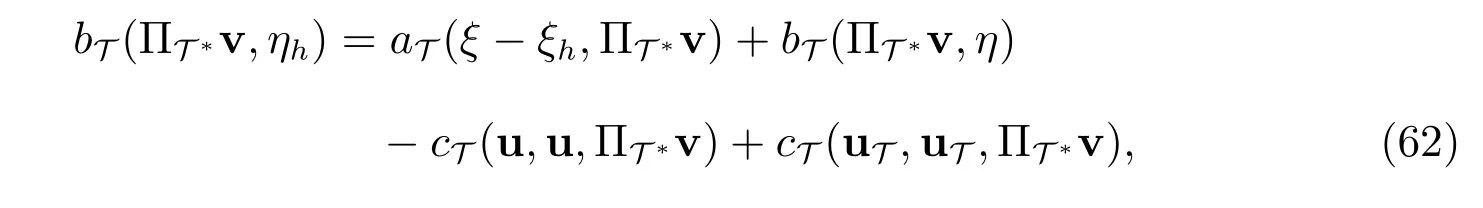
其中

下面考虑等式(63)右端各项的估计.注意到

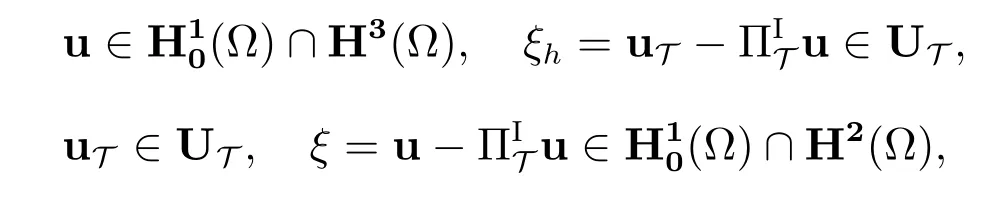
则由估计(32)和(33)知

将以上估计(65)代入等式(63)的右端可得

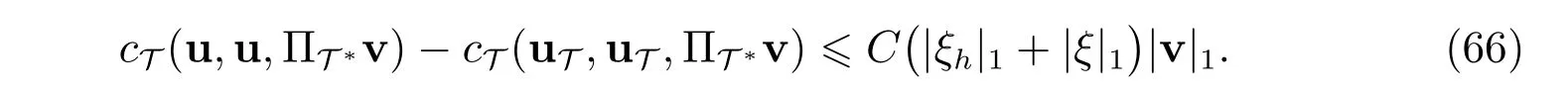
由估计(13)可知，对任意的(v,η)∈(UT,(Ω)∩H1(Ω))，有

由估计(14)可知，对任意的(ξ −ξh)∈∩H2⊂∩，有

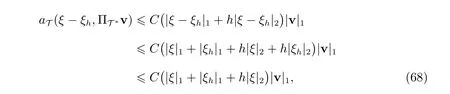
此处用到了有限元逆估计|ξh|2Ch−1|ξh|1, ξh ∈UT.

将以上估计(66),(67),(68)代入等式(62)的右端，并利用插值误差估计可得

又由引理3 中的估计(12)可知，对任意的ηh=pT −p ∈QT，有

结合(69)和(70)易得

即得估计(61).

定理2的证明：利用引理7 和引理8 的结论，得到|u−uT|1和//p −pT //0的估计.

首先由估计(43)和(61)易知

为了方便，记|||(u,p)|||:=h2(//u//3+//p//2)，则利用Young 不等式可得

此处ε>0 为一任意常数.取ε=C，则利用不等式(72)，估计(71)可化为

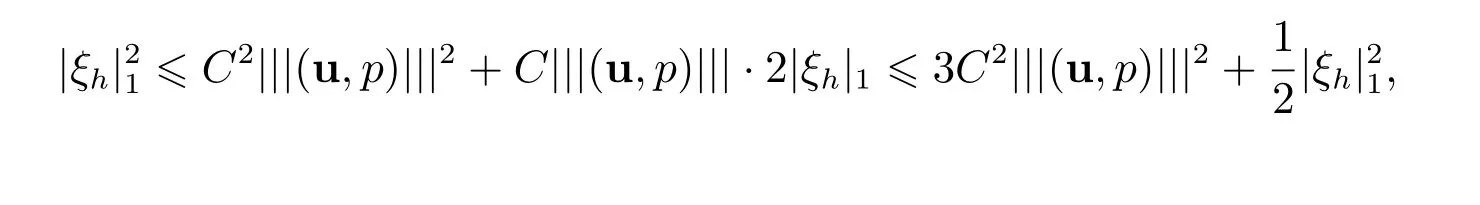
即

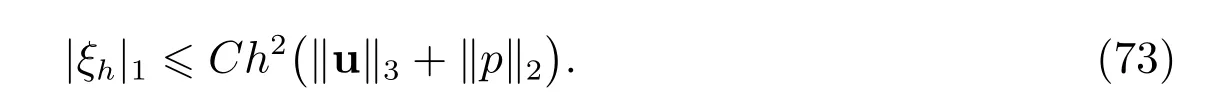
因此，利用三角不等式，插值误差估计和估计(73)可得

另一方面，结合估计(73)和(61)，利用三角不等式及插值误差估计可得

因此由估计(74)和(75)即得结论(42).

此定理说明，当µ和f 满足条件(40)或(41)时，FVM(6)存在唯一解且具有最优误差估计.进一步分析可以发现条件(41)意味着C1C3C6>//f//0，即要求//f//0不宜过大.另外，在实际问题中粘度往往非常小，从而条件(41)的第一个不等式可恒成立，也就是条件(40)的第二个不等式可恒成立.因此只需考虑条件(40)的第一个不等式，即条件(20)的第二式.综合前述的稳定性，可知当µ和f 满足条件(20)时，原问题(1)有解，且FVM(6)存在唯一解及其最优误差估计.

此定理的证明具有一般性.这种方法可以直接应用到更一般的高阶及高维情形的误差估计证明.

5 算例

本节将利用数值算例来检验FVM(6)的有效性.

步骤1取迭代初值:=0(n=0)代入方程(76)，求解对应的线性方程(即Stokes方程)可得.显然满足条件(21).

为非线性方程FVM(6)的解.

下面检验FVM(6)在三角形网格上的误差估计.考虑将正方形区域Ω := (0,1)×(0,1)进行一致三角形网格剖分，网格大小为h=1/N.具体地，先将Ω 分解成N×N个矩形网格，然后用对角线将每个正方形分成两个三角形.两个算例如下.

例1 设N-S 方程(1)的真解为u=(u1,u2)和p，其中

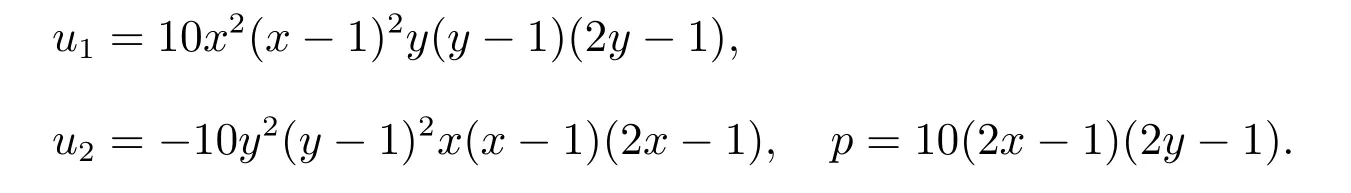
例2设N-S 方程(1)的真解为u=(u1,u2)和p，其中

例1 和例2 中的解均满足条件u|∂Ω=0,∫Ωp=0.

为使N-S 方程(1)中的µ和f 满足条件(20)的第二式，此处取µ=1.表1 和表2 分别列出了例1 和例2 的数值计算结果，其中|u−uT|1, //p −pT //0分别为速度场的H1模和压强场的L2模误差，r(u), r(p)分别表示速度场与压强场所对应的误差收敛阶.数值结果表明本文的计算方法正确，且当网格逐渐加密(满足条件(20)的第一式)时，FVM(6)具有速度项的最优H1模和压强项的最优L2模的误差收敛阶O(h2)，显然这与本文的理论结果相一致.从而也验证了求解N-S 方程(1)的二阶混合FVM(6)与相对应的有限元法具有相同的误差收敛阶.

表1 例1 的误差估计和收敛阶

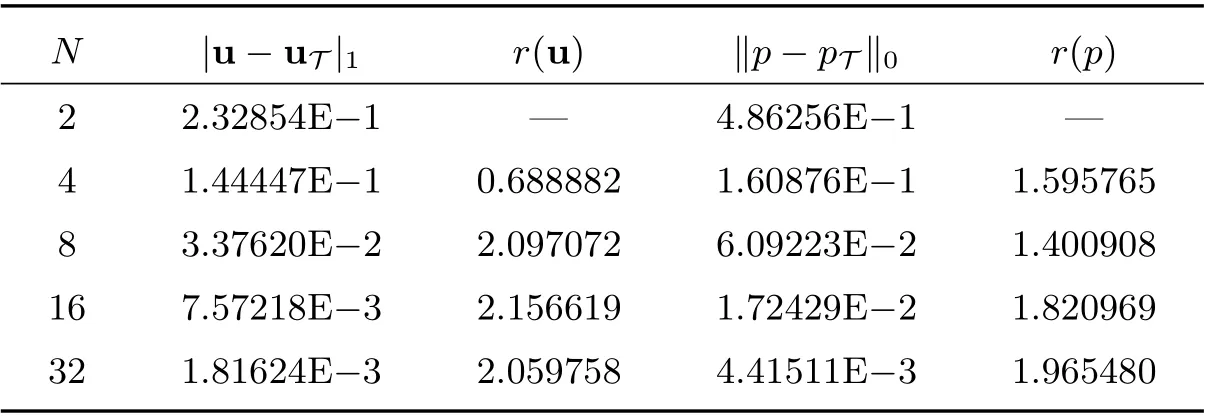
表2 例2 的误差估计和收敛阶

下面考虑在正方域Ω = (0,1)×(0,1)上利用FVM(6)对经典lid-driven cavity 问题进行数值模拟.

例3 设N-S 方程(1)中的µ=1,f =0.真解u=(u1,u2)满足如下边界条件

显然，N-S 方程(1)中的µ和f 满足条件(20).利用GMSH 软件自动生成区域Ω 的非结构三角形网格剖分，见图1.根据FVM(6)的数值计算结果，利用TECPLOT 软件画出了其速度场的流线图，见图2.从流线图中可以看出，对于具有粘性(系数µ= 1)的方腔驱动流体，当边界以一定的速度移动时，方腔内会产生一个漩涡流，且漩涡中心位于方腔的中间位置.流线的疏密可反映速度的大小，因此可见靠近方腔驱动壁面上的速度要大于其它地方的速度.总之，模似结果显示出了良好的计算效果.

图1 三角形网格剖分

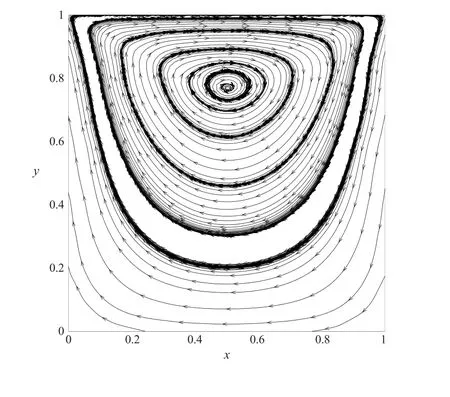
图2 速度场流线图

6 结论

由定理1 和定理2 可知，当µ和f 满足适当的条件时(类似于但略强于有限元法)，例如条件(20)，则求解N-S 方程(1)的FVM(6)存在唯一解及其最优误差估计.在有限体积法中，µ和f 所需满足条件略强于对应的有限元法，这主要是由有限体积法的椭圆离散双线性型的不对称性所引起的，因此这是不可避免的.不过有限体积法可以保持物理量的局部守恒性(这是传统有限元法不具备的)，且计算量比有限元法(尤其是间断有限元法)小得多，这正是利用有限体积法处理CFD 问题的优势所在.