惯量松弛因子在格子Boltzmann 方法中的应用

王颖娟, 龚光彩, 石 星, 龚子彻, 刘永超

(湖南大学土木工程学院，长沙 410082)

1 引言

格子Boltzmann 方法(LBM)是近年来发展较迅速的一种新型数值计算方法，不同于传统的计算流体力学方法，它是一种介于宏观与微观之间的介观方法[1]，主要有以下优点：算法简单、编程容易、能够处理复杂的边界条件、具有良好的并行性、能直接模拟有复杂几何边界的诸如多孔介质等连通域流场，无需作计算网格的转换等等.LBM 是早期的格子气自动机模型的拓展[2]，现在已经是一种理论比较完备、模型比较成熟的数值模拟方法，目前被广泛应用在了多个领域，包括：热效应[3]、层流，湍流模拟[4]、复杂边界以及动边界[5]等等，同时格子Boltzman 方法也可以解决传统计算方法中比较难模拟的多孔介质的问题，将在工程材料与能源利用领域有着重要应用.

惯量松弛因子一般运用在解决N-S 方程中，在SIMPLE 算法中加入惯量松弛因子能加快程序收敛速度，提高稳定性，并且有一定的适应非均匀网格的能力[6,7].对于较为复杂的流动，传统格子Boltzmann 方法往往需要足够多的网格点来计算流场，以便更好的捕捉流场信息，但同时也会增加计算量，使得计算效率降低.为了解决传统格子Boltzmann 方法效率低的问题，笔者首次讨论了将惯量松弛因子与格子Boltzmann 方法结合，以顶盖驱动方腔流为校核算例，对不同惯量松弛因子下的格子Boltzmann 方法开展数值算法研究及对应的算例验证，探究惯量松弛因子在格子Boltzmann 方法中的作用及其影响.

2 惯量松弛因子与格子Boltzmann 模型

2.1 惯量松弛因子与LBGK 模型

LBGK 模型是目前应用比较广泛的格子Boltzmann 模型，Qian 等[8]提出的DmQn 模型(m维空间，n个离散格子速度)最为典型，为了保证各向同性、伽利略不变性及不可压N-S 方程中速度对压力的独立性，本文采用LBGK 的D2Q9 模型[9]，其演化方程为

其中fk(x,t)是ck方向的粒子密度分布函数；fkeq(x,t)是在t时刻x处的平衡态分布函数；ω为松弛频率；ck为粒子速度矢量.

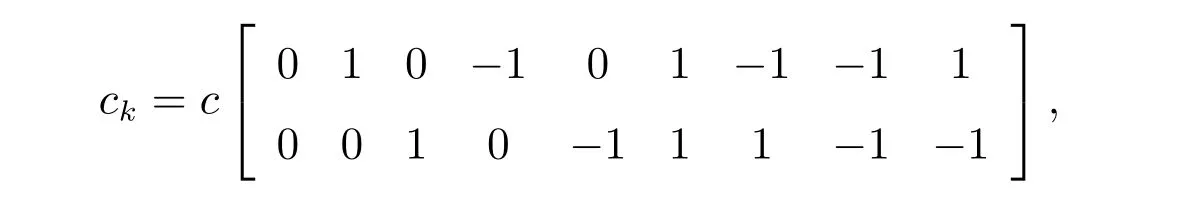
其中格子速度c=δx/δt.宏观速度、体积平均密度可以由分布函数得出

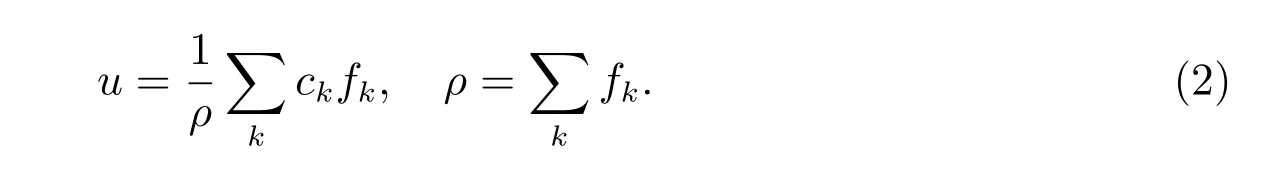
平衡态分布函数为

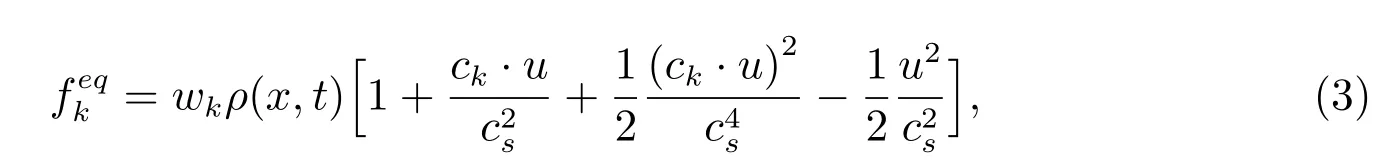
通过Chapman-Enskog 展开，可以得到运动粘性系数与松弛频率的关系为

LBM 方法包含两个步骤：碰撞和迁移.

1) 碰撞步骤的迭代格式如下

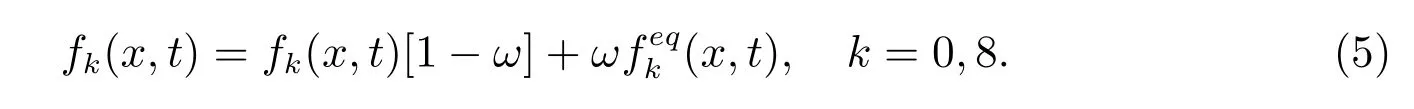
在上式中引入惯量项Rfk，在迭代过程中，上式的迭代格式成为

其中R为惯量松弛因子.

2) 迁移步骤如下

2.2 多松弛格子Boltzmann 模型

在LBGK 模型中，当松弛时间过大时，会出现数值不稳定的情况，因此为了克服这一缺点，法国学者[10]提出了一个广义格子Boltzmann 模型，即多松弛格子Boltzmann 模型(MRT-LBM).

其中f 是一个矢量，代表格子节点上的速度分布函数，m 代表一系列相互独立的矩，meq是矩m 的平衡态值，M是一个正交的转换矩阵，可把f 转换为m

其中

松弛矩阵

3 物理模型

本文采用顶盖驱动流作为校核算例，它是一个经典的不可压缩流动，其结果广泛得到了验证.图1 为二维方腔顶盖驱动流的示意图，在实际计算中，参考文献[9]中的顶盖驱动流的格子Boltzmann 程序，并且对采用不同惯量松弛因子的计算格式进行代码编译，边界处理采用标准反弹格式，程序收敛判据如下

其中error 为两个相邻时层速度的最大相对误差；ux(i,j,t)为点(i,j,t)处沿x轴方向的宏观速度；uy(i,j,t)为点(i,j,t)处沿y轴方向的宏观速度；ε为一个小量.

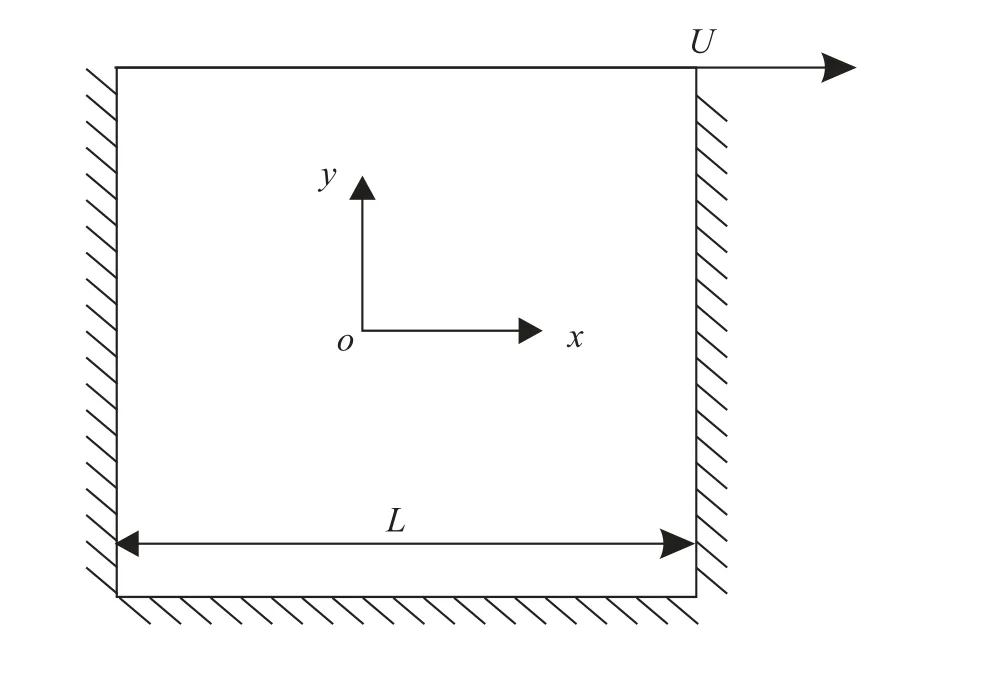
图1 二维顶盖驱动方腔流示意图

在标准的D2Q9 格子Boltzmann 模型模拟中，顶盖驱动速度U=0.1，网格为100×100，运动粘度系数由雷诺数Re 定义式反算得到，各参数均为格子单位，例如对雷诺数Re 取1000，ε则取7.5E−6.笔者分别采用了LBGK 与多松弛的格式对方腔流的流函数等值线、中轴线上的速度等进行结果对比；同时在D2Q9 的LBGK 模型中加入惯量松弛因子，并分别给出了不同惯量松弛因子下的收敛步数、流函数等值线图、以及记录涡心的坐标，并将计算结果与不加惯量松弛因子的结果进行比较分析；最后对三维的顶盖方腔流进行了模拟计算，研究惯量松弛因子在三维格子Boltzmann 中的作用.

4 计算结果及分析

4.1 D2Q9 的LBGK 模型与MRT-LBM 模型

笔者分别采用D2Q9 的LBGK 模型和多松弛的格子Boltzmann 模型对顶盖驱动方腔流进行模拟，其中MRT-LBM 模型的程序是参考文献[9]中附录里的计算机代码，雷诺数取1000，图2 为两种模型方法所求得的流函数等值线对比图，从图中可以看出两种模型所求得的流函数图趋势基本一致，当流体稳定后，方腔中央、左下角和右下角都分别有一个涡.表1 为两种模型的涡心坐标与基准解的比较，基准解为文献[11]中的模拟结果，可以论证两种模型程序的正确性.

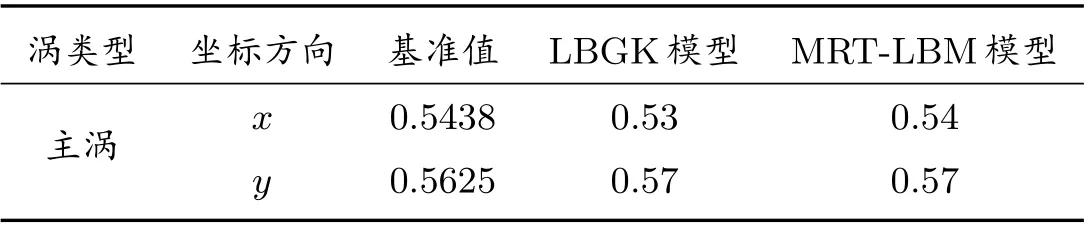
表1 数值模拟结果对比

图3 表示两种模型所求得的水平、垂直两条中轴线上的速度对比图，从图中可以看出，两种模型的中轴线上的速度曲线吻合的很好，基本重合一致.

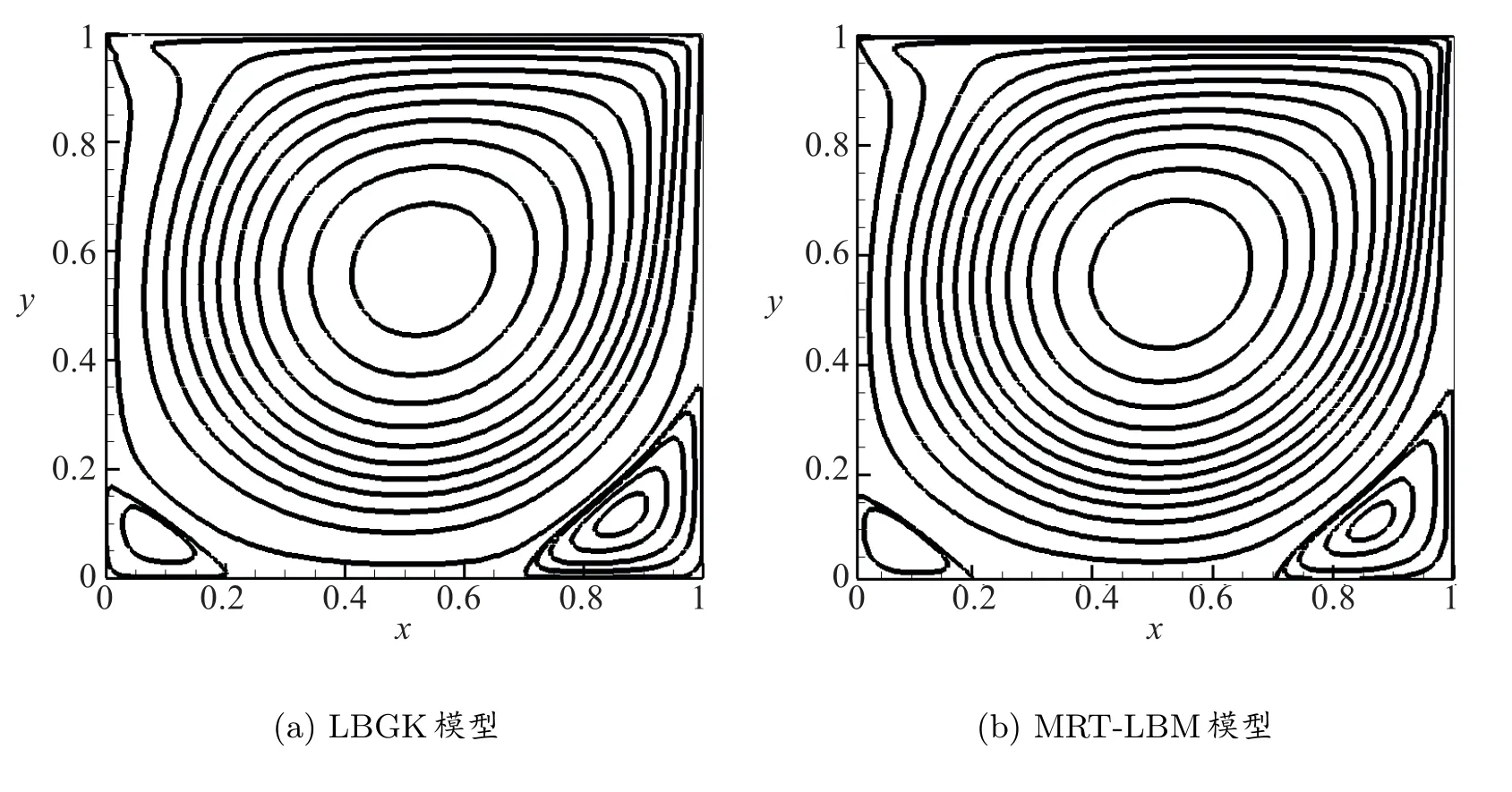
图2 LBGK 模型和MRT-LBM 模型的流函数等值线对比图

图3 两种模型中轴线上的速度对比

4.2 惯量松弛因子在D2Q9 的LBGK 模型中的应用

表2 表示雷诺数分别取400、1000 时，不加惯量松弛因子与加不同惯量松弛因子下的收敛迭代步数与计算结果偏差的对比，图4 为收敛步数与惯量松弛因子的关系曲线图，其中R= 0 为不加惯量松弛因子的模拟结果，从表中可以看出：当惯量松弛因子R大于0.03 时，程序收敛步数随着惯量松弛因子的增大在不断的减少，相应提高的计算效率也越来越高，最高达到了50%；且随着雷诺数的增大，在相同的惯量松弛因子下程序所提高的效率也在增大；同时经研究发现当惯量松弛因子R取0.01 到0.02 时，我们发现程序的运行结果难以达到收敛精度，但程序并不发散，这表明惯量松弛因子无论是运用在SIMPLE 算法中还是运用在格子Boltzmann 中都有其适宜的取值区间，因此惯量松弛因子R取0.02 时是其极限的取值下界.

表2 不同惯量松弛因子下的收敛步数与计算误差

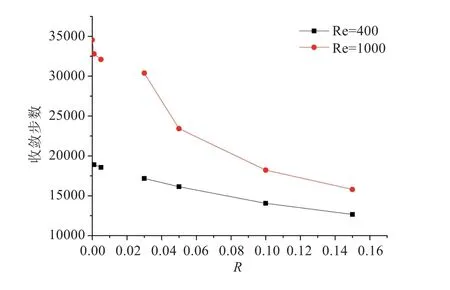
图4 收敛步数与惯量松弛因子的关系曲线

图5、图6 分别为雷诺数取400、1000时，取不同惯量松弛因子下的水平、垂直两条中轴线上的速度与不加惯量松弛因子的该速度进行比较，从图中可以看出：当惯量松弛因子R等于0.03 时，计算结果的偏差在10%以内；当惯量松弛因子R等于0.05 时，计算结果的偏差在15%以内；当R等于0.1 时，计算结果的偏差在25%以内；因此随着惯量松弛因子R的增大，中轴线上的速度偏差也越来越大；而且随着雷诺数的增大，取不同惯量松弛因子之间的误差相对也会增大一点，但都在可接受范围之内.将加了惯量松弛因子的LBGK 模型与MRT-LBM 模型进行对比可以发现，当惯量松弛因子取0.03 和0.05 时，中轴线上的速度与MRT-LBM 模型中轴线上的速度非常接近.

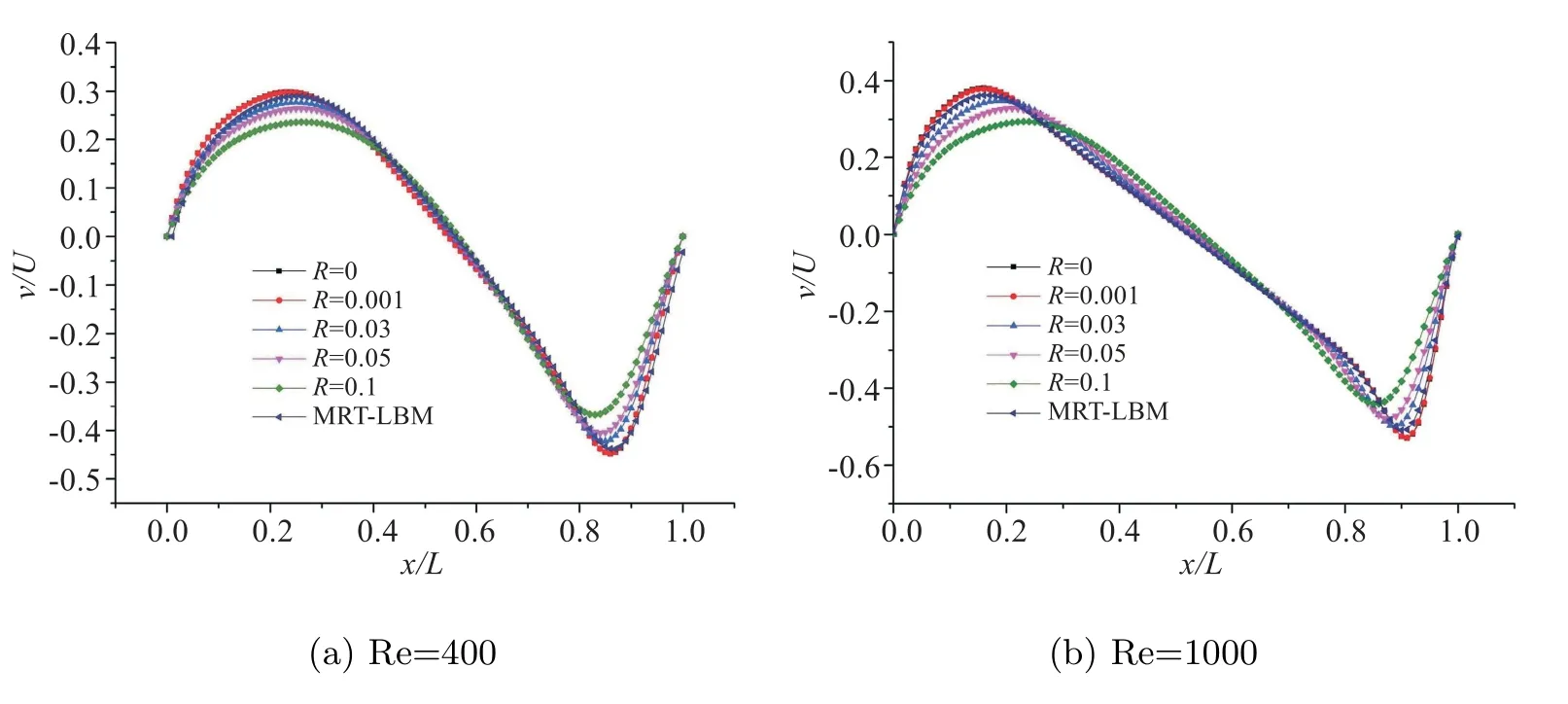
图5 水平中轴线上的速度对比

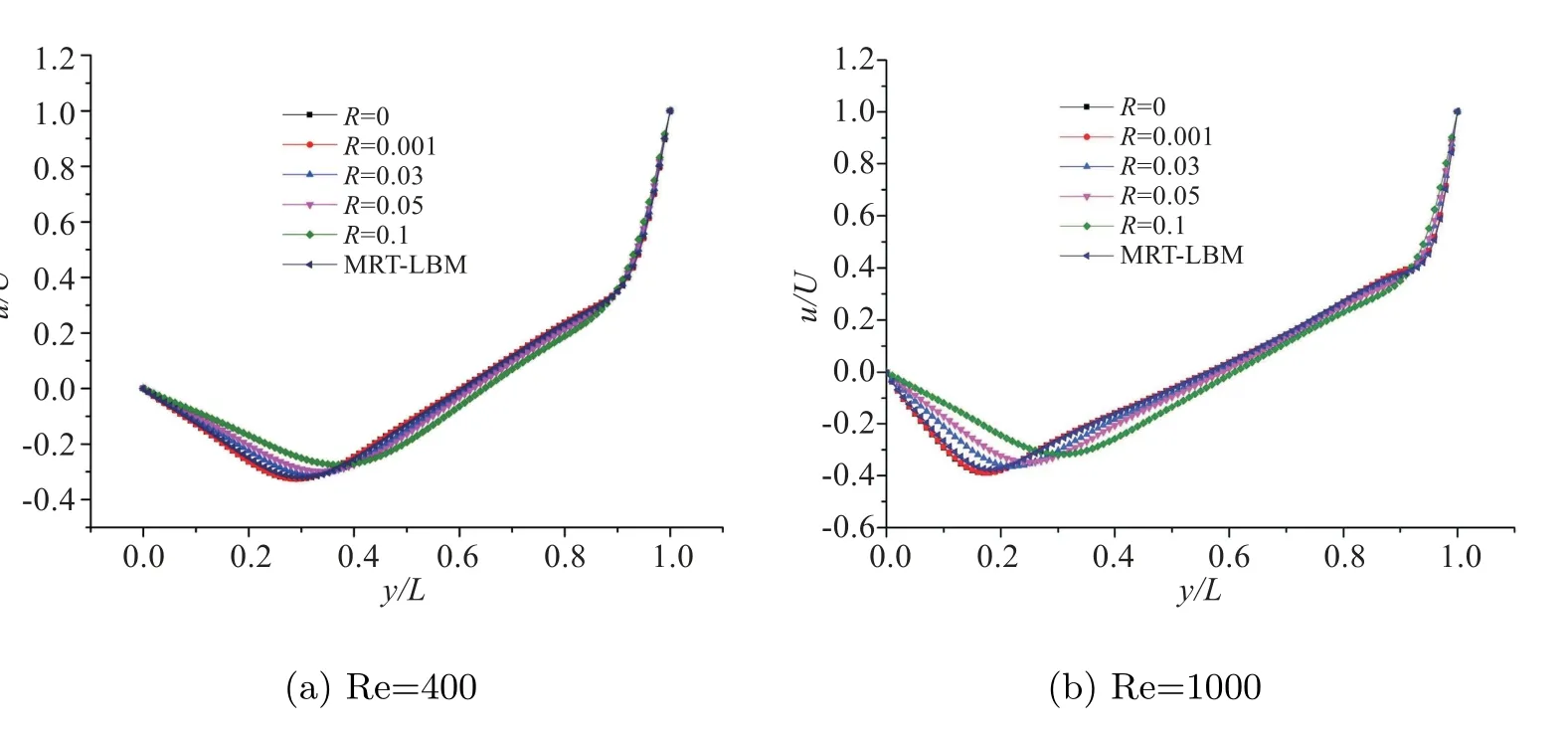
图6 垂直中轴线上的速度对比

图7 给出了雷诺数取1000 时，不加惯量松弛因子与加不同惯量松弛因子下顶盖驱动流的流函数图，从图中可以清晰的看到：流动稳定后，方腔的中央都有个一级大涡，而且左下角和右下角也都分别有一个二级涡；但随着惯量松弛因子的增大，中心涡涡心有由方腔中心逐渐向方腔中心偏右上方移动的趋势；同时当惯量松弛取0.03 和0.05 时，流线图与MRT-LBM 模型的流线图较为接近.

为了量化以上结果，笔者测试了方腔中央的一级涡以及左右下角附近的两个涡的涡心坐标，结果列于表3，同时表3 也列出了不同雷诺数下有无惯量松弛因子的计算结果与基准解的比较，其中a、b、c 分别代表文献[11–13]中的模拟结果，从表中可以看出：不加惯量松弛因子的模拟结果与其他文献的模拟结果吻合得很好，从而也进一步验证了该算法程序的准确性；虽然随着惯量松弛因子R的增大，三个涡心坐标偏移也在增大，但误差基本都在可接受范围以内，当惯量松弛因子R取0.03 到0.05 之间时，一级涡涡心坐标误差在5%以内；当惯量松弛因子R取0.1 时，一级涡涡心坐标误差在8%之内；当惯量松弛因子R取0.15 时，一级涡涡心坐标误差在12%以内.

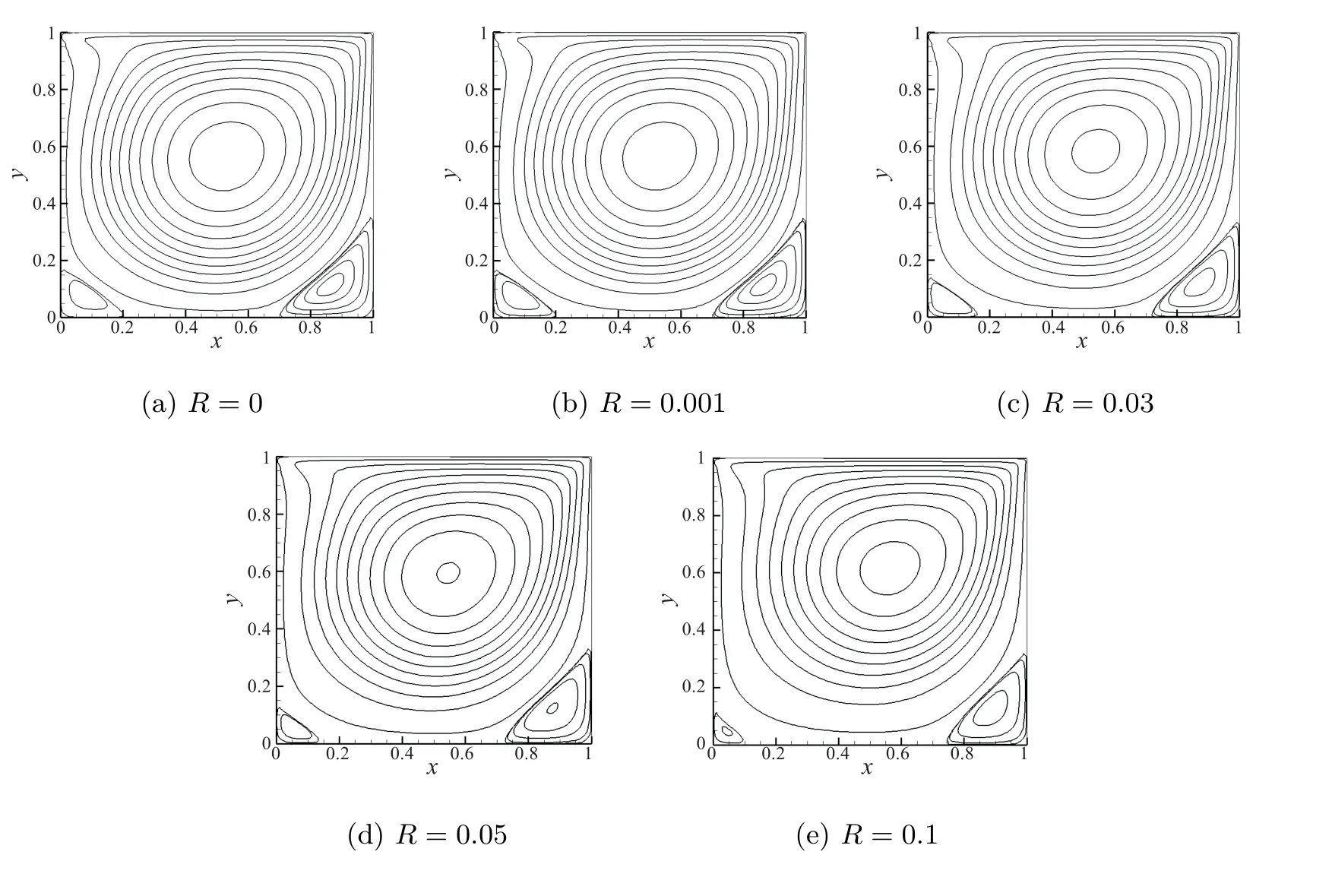
图7 不同惯量松弛因子下顶盖驱动流的流函数等值线图

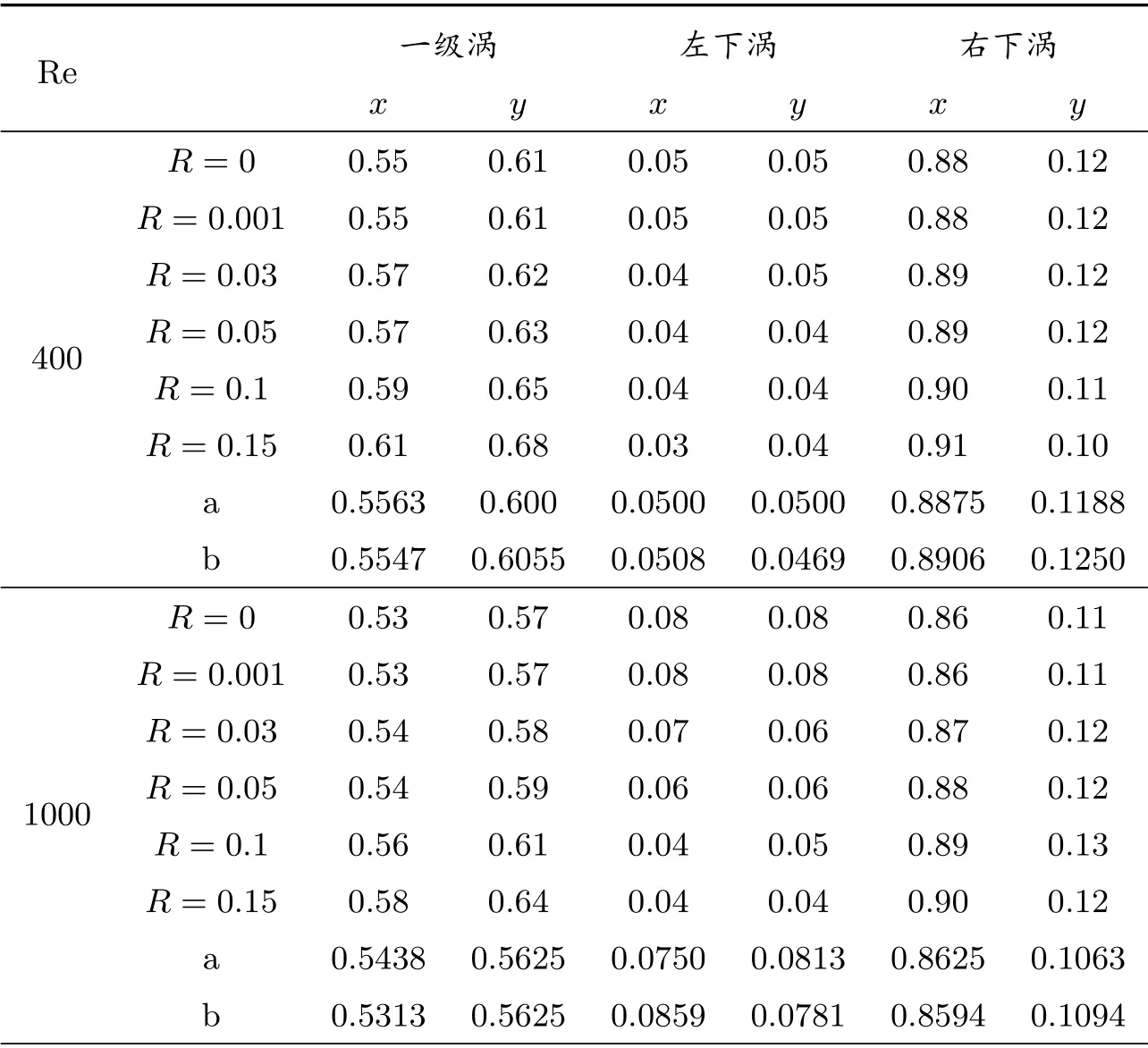
表3 顶盖驱动流的涡的位置

续表3 顶盖驱动流的涡的位置

4.3 惯量松弛因子在D3Q15 的LBGK 模型中的应用

笔者还采用了LBGK 的D3Q15 模型对三维顶盖驱动流进行了模拟，并将惯量松弛因子与格子Boltzmann 方法结合，研究惯量松弛因子在三维格子Boltzmann 方法中是否也具有通用性.对于三维LBGK 模型，当雷诺数Re 取1000、ε取1.0E−12、惯量松弛因子分别取0、0.03 和0.1 时的收敛步数，如表4 所示，随着R值增大，提高的计算效率也越来越高.

表4 不同惯量松弛因子下的收敛步数

图8 至图10 为不同惯量松弛因子下顶盖驱动流流线的不同视角图，将不加惯量松弛因子的流线分布与文献[14]中的流线分布进行了对比，可以看出两者不同视角的流线图基本一致，验证了程序的正确性；当惯量松弛因子取0.03 和0.1 时，空腔流线与不加惯量松弛因子时的空腔流线基本一致；但当R值增大，其在计算效率提升的同时，中心涡的涡心坐标也有向右上方偏移的趋势.综上惯量松弛因子在三维格子Boltzmann 方法中一样具有通用性.

5 结论

惯量松弛因子一般在N-S 方程中发挥作用，但在格子Boltzmann 方法中依然可以发挥极大的作用.以二维顶盖驱动流为例，分别采用不同雷诺数、不同惯量松弛因子进行了数值模拟，并将计算结果与基准解进行了比较，可以看出惯量松驰因子R存在一个合理的最佳区间，当惯量松弛因子取0.03 时，计算误差在10%以内；惯量松弛因子取0.05 时，计算误差在15%以内；当惯量松弛因子取0.1 时，计算误差在25%以内；且随着惯量松弛因子的增大，计算效率也在大幅度提高；但研究也发现当惯量松弛因子取0.01 到0.02 之间时，程序收敛速度会不稳定.综上所述惯量松弛因子R的下限建议取0.02，并且不宜大于0.1，同时其最佳取值区间为0.03 到0.05.

笔者首次讨论了将惯量松弛因子与格子Boltzmann 方法结合，研究表明它能有效解决格子Boltzmann 方法中LBGK 模型效率低的问题，并且具有通用性，MRT-LBM 模型较LBGK 模型而言数值更为稳定，在LBGK 模型中加入惯量松弛因子与MRT-LBM 模型所得结果较为接近，因此将惯量松弛因子引入到格子Boltzmann 方法中能在保证一定精度的前提下提高收敛速度、加快程序计算效率等，使其能在工程材料与能源环境领域发挥重要应用.

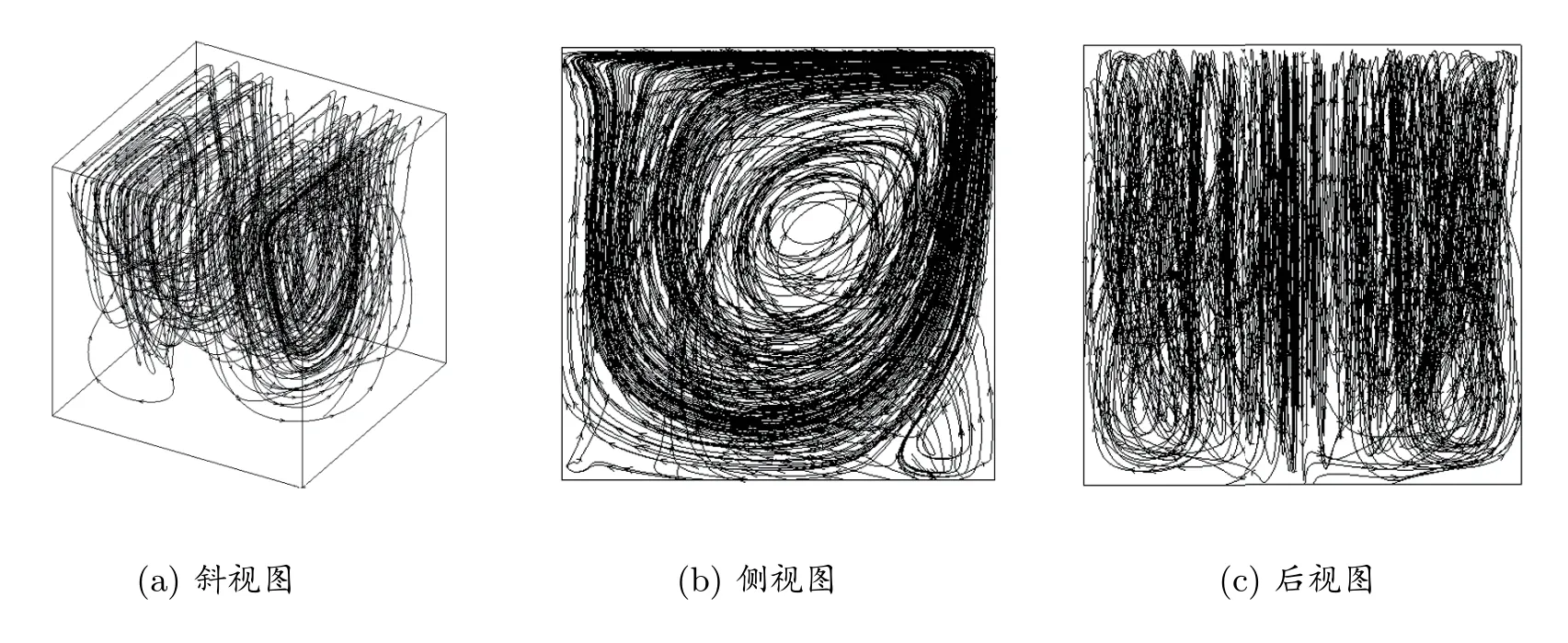
图8 R=0 时流线分布的不同视角

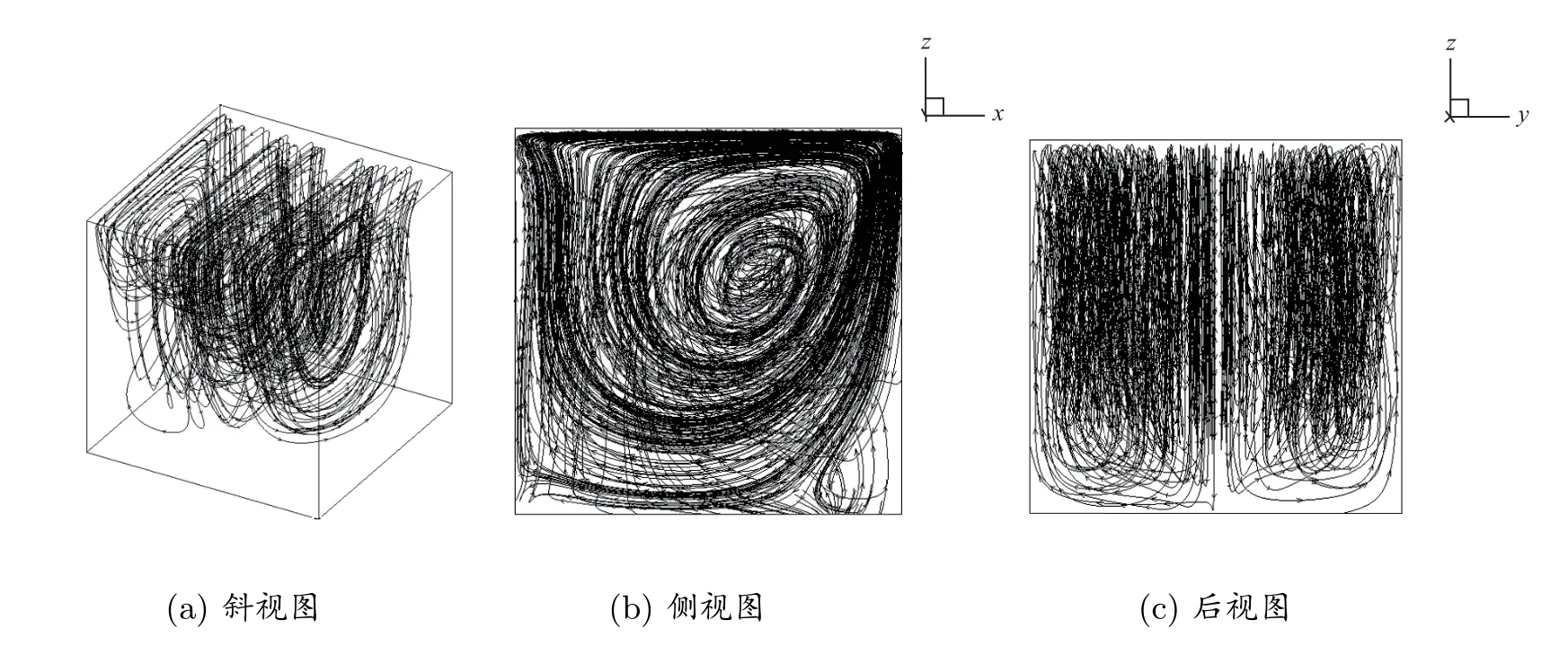
图9 R=0.03 时流线分布的不同视角

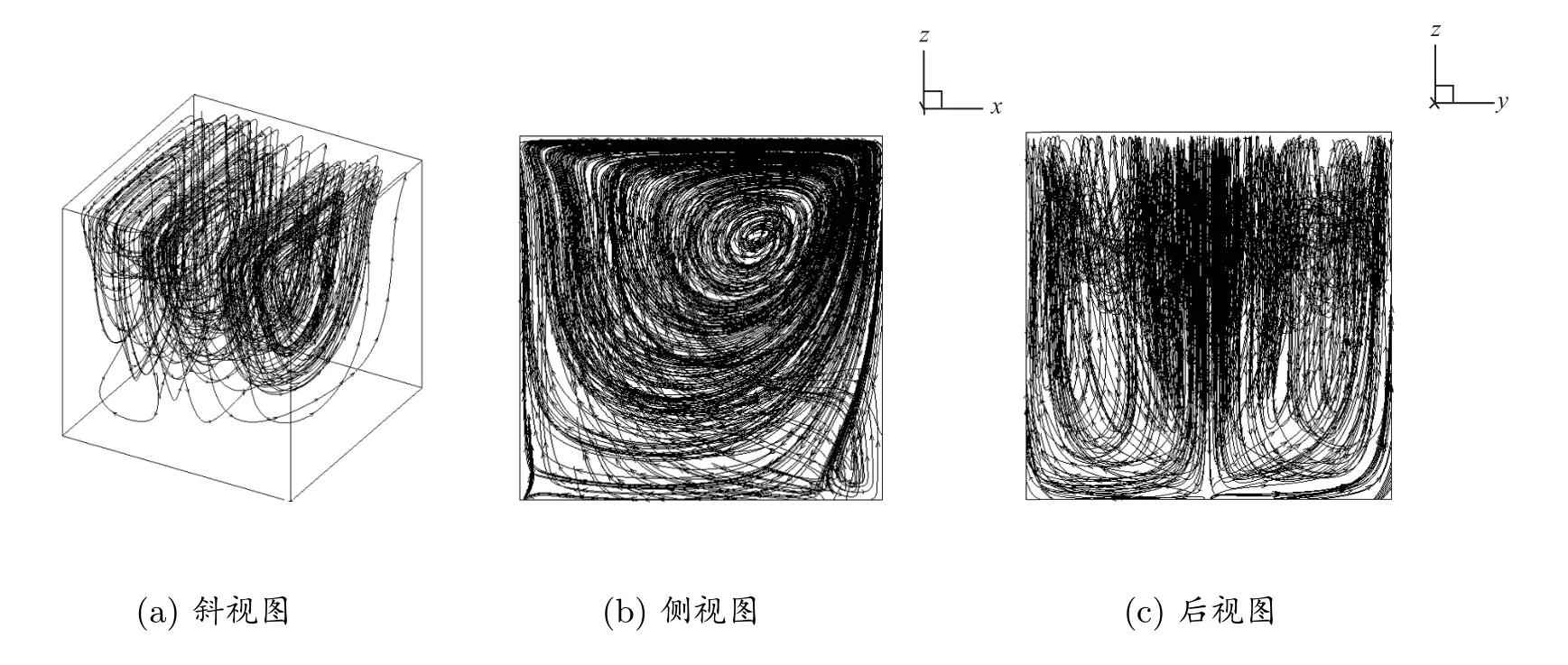
图10 R=0.1 时流线分布的不同视角