偏正态数据下联合位置、尺度、偏度模型的统计诊断
2021-05-07吴刘仓聂兴锋郑桂芬
吴刘仓, 聂兴锋, 郑桂芬
(昆明理工大学理学院,昆明 650093)
1 引言
目前,对均值参数建模的理论和方法都研究得比较透彻[1-6],但在现实生活中我们会发现,同方差数据只占少数部分,大多数还是异方差数据,这表明对方差参数建模同样很重要,对方差参数建模能够很好的了解方差的来源,以此来达到有效的控制方差[7].另一方面,在这大多数的异方差数据中大部分并不具有严格的对称性,而是具有一定偏斜的,这时我们再用正态分布去描述它们的性质就不太适合了.近年来,偏正态分布[8]成为非对称分布研究的重要分支.因此,偏态数据的统计推断也随之成为统计学探索的热点问题.
我们知道,统计诊断是数据分析的第一步,主要目的就是对样本数据中异常点或强影响点的诊断与识别.传统的判断异常点的方法有Cook 距离、似然距离、W-K 统计量、AP 统计量等.而文献[9]中提出了一种新方法Pena 距离,文献[9]所提方法与传统方法有较大差别.传统的方法是删除一个样本点,对估计值的影响,或者是某个样本点的微小扰动对估计值的影响,而Pena 距离则是研究样本中某一个样本点受其余各个样本点的影响,简单来说,就是样本中各点删除后,对某一特定的点的预测值的影响.
Pena 距离的研究方面:孟丽丽和卢志义[10]基于Pena 距离关于加权最小二乘估计的影响分析做了研究;胡江等[11-13]基于Pena 距离研究了非线性回归模型以及广义回归模型的影响分析.异方差的研究方面:Aitkin[14]基于异方差模型研究了正态分布下的极大似然估计;戴琳等[15]基于联合均值与方差模型研究了统计诊断;马婷等[16]基于SN 分布联合位置、尺度、偏度模型研究了极大似然估计;吴刘仓等[17,18]基于StN 分布下联合位置、尺度、偏度模型研究了极大似然估计以及基于偏正态数据下联合位置与尺度混合专家回归模型研究了参数估计;Lachos 等[19]基于SN 分布的混合尺度异方差非线性回归模型研究了参数估计与统计诊断.偏态数据的统计诊断方面:基于Cook 距离、似然距离等,Xie 等[20]研究了SN 分布下非线性均值回归模型的统计诊断;万文等[21]基于偏正态数据下联合位置与尺度模型研究了统计诊断.李玲雪等[22]缺失偏态数据下联合位置与尺度模型研究了统计推断;李世凯等[23]偏态数据下混合非线性回归模型研究了统计推断.但是偏正态数据下联合位置、尺度、偏度模型的异常点诊断和识别还没有人研究,而统计诊断又是处理数据必不可少的一部分.因此,基于SN 分布下联合位置、尺度、偏度模型的统计诊断进行研究,得出了比较有价值的相关结果.
2 偏正态数据下联合位置、尺度、偏度模型的极大似然估计
2.1 偏正态分布
1985 年Azzalini[8]首次研究提出偏正态分布,若随机变量Y服从偏正态分布,即Y ∼SN(µ,σ2,λ),其中µ表示位置参数,σ表示尺度参数,λ表示偏度参数,则其概率密度函数可表示为

其中φ(·),Φ(·)分别表示标准的正态分布的密度函数和分布函数.当偏度参数λ= 0 时,密度函数(1)退化为正态分布的密度函数,即此时偏正态分布退化为正态分布.在偏正态分布中有

2.2 基于偏正态数据的联合位置、尺度、偏度模型
本文研究以下偏正态数据的联合位置、尺度、偏度模型
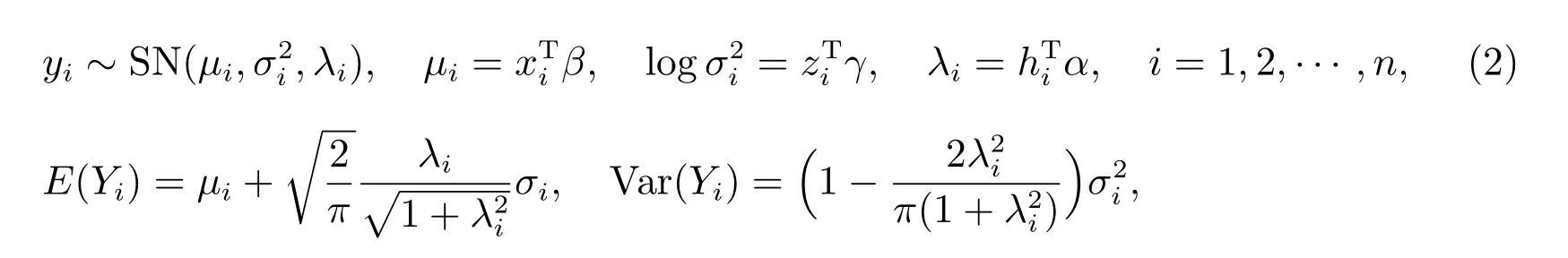
其中yi是被解释变量,服从SN 分布,xi=(xi1,xi2,··· ,xip)T, zi=(zi1,zi2,··· ,ziq)T,hi= (hi1,hi2,··· ,hir)T是与yi有关的解释变量.β= (β1,β2,··· ,βp)T是与位置模型有关的p× 1 维向量,γ= (γ1,γ2,··· ,γq)T是与尺度模型有关的q× 1 维向量,α=(α1,α2,··· ,αr)T是与偏度模型有关的r×1 维向量,xi, zi, hi三个解释变量的观测值可以相同,可以不同或部分相同.本篇文章主要研究模型(2)的统计诊断方法.
2.3 极大似然估计
假设(yi,xi,zi,hi)为样本中的第i个样本点,由密度函数(1)及模型(2)可知其密度函数为
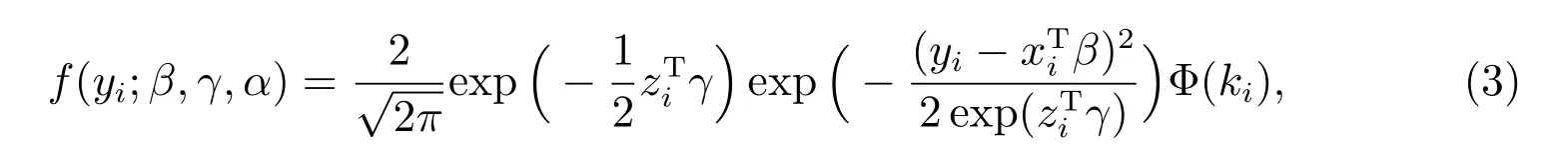
其中
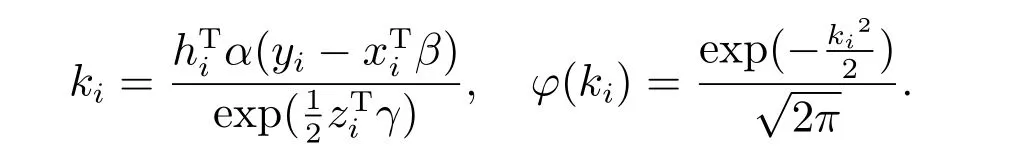
由(3)式可得其似然函数表示为
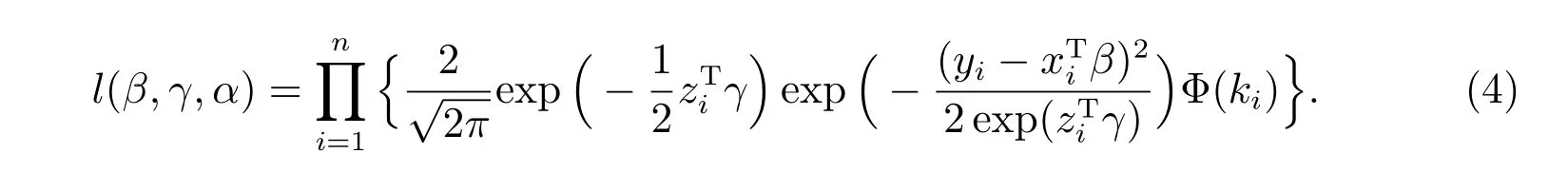
上式两边取自然对数,就得到对数似然函数为
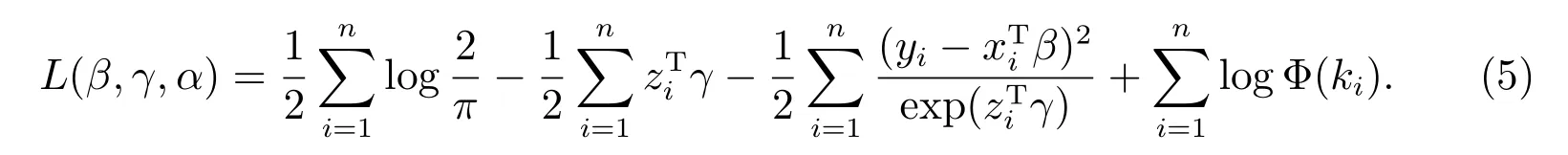
令θ=(βT,γT,αT)T,则L(β,γ,α)=L(θ),因此

由Gauss-Newton 迭代方法可获得相应参数的估计值.设我们未删除模型参数估计值用,,表示,.删除模型的参数估计值则可以用表示,,即删除第i个点后的参数估计值.,则表示删除第j个数据点后第i个数据点的参数估计值.
2.4 基于数据删除模型的统计诊断量
2.4.1 似然距离及其计算
在数据删除模型框架下,似然距离是与Cook 距离同等重要的诊断统计量.由于似然距离的定义并不限于线性模型,故而可以用于相当广泛的统计模型,诸如非线性模型、广义线性模型等.针对本文中的删除模型,第i个点的似然距离定义为

由于L(ˆθ)为全局最优解,因此LDi ≥0 恒成立.似然距离反应了第i个数据点(xi,yi)对参数θ的极大似然估计的影响.对于远大于其似然距离的点,则为异常点或强影响点.由于似然距离没有显示解,因此需要用近似解代替其数值解.对(6)式在处利用泰勒展开可得
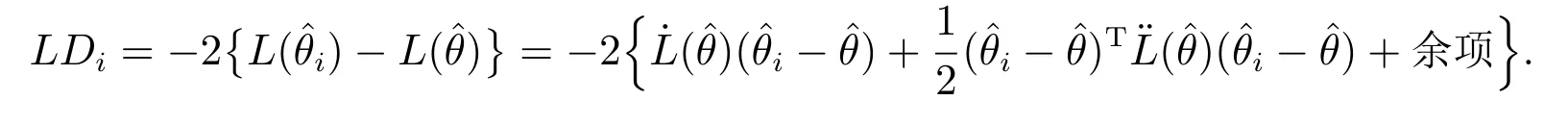
由于˙L(ˆθ)=0,从而得到似然距离(LD)的近似表达式如下
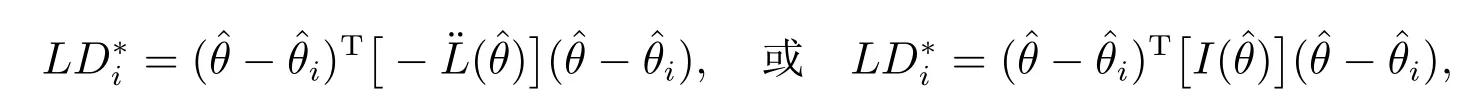
其中I()为Fisher 信息阵,为方便计算,本文使用Fisher 阵计算似然距离L.
2.4.2 Cook 距离及其计算
Cook 距离是统计诊断中非常重要的诊断统计量之一,是Cook 于1977 年基于参数置信域的统计意义提出来的.针对本文中的删除模型,第i个点的Cook 距离定义如下
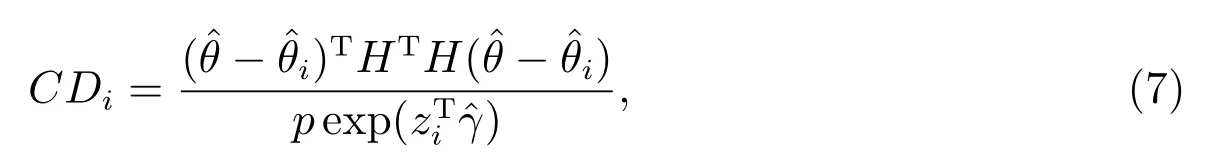
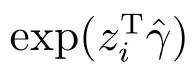
2.4.3 Pena 距离及其计算
Pena 距离是Pena 于2005 年提出的一种诊断统计量.常见的统计诊断方法有数据删除诊断和局部影响分析,数据删除是针对完全数据的,主要考察删除某一个或某一组样本点对既定模型参数估计的影响,即对模型回归分析和预测分析的影响.局部影响分析是对模型施加一个微小扰动,然后研究样本点对模型参数估计和预测的影响.而Pena 距离则是研究样本中某一点受其余各点的影响,即删除样本中的各点对某一既定样本点的预测值的影响,也是基于数据删除模型的诊断分析,是对诊断统计量的重要补充.
根据文献[9],Pena 距离定义如下
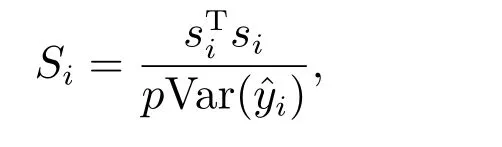
定理1偏正态数据下的Pena 距离

其中为第j个学生化残差(标准化残差).
证明 根据文献[9]

定理2当样本中不含有异常点时,有
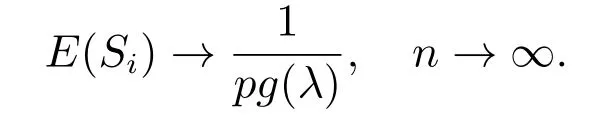
证明
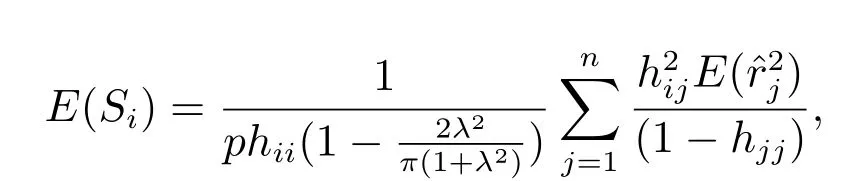
由文献[24]可知:E()=1,故
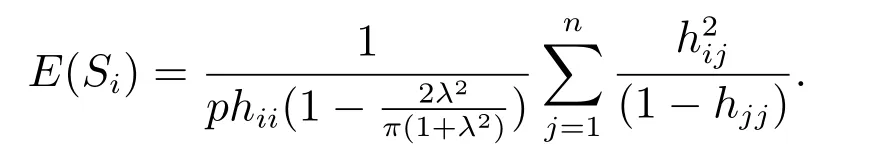
记
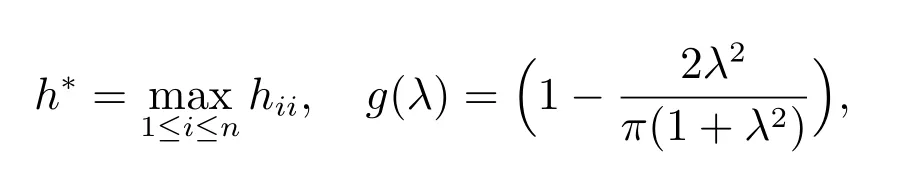
我们有
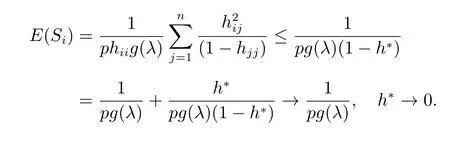
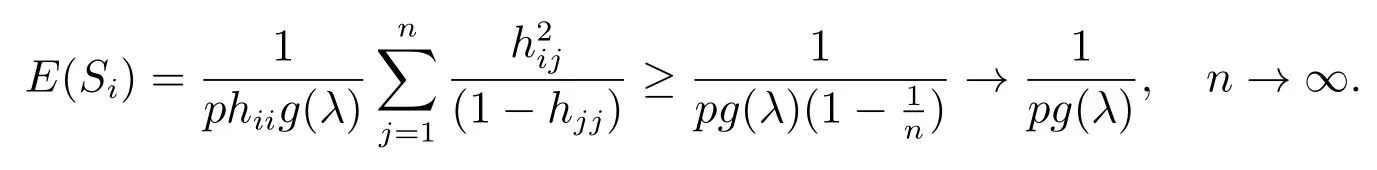
综上所述,当样本中含有高杠杆异常点时,统计量Si的期望,有:
1)E(Si)→0,高杠杆异常点;
当数据中含有一簇相同的高杠异常点时,可根据Si的值很容易找到它们但Cook 距离不能识别.特别地,当λ= 0 时,g(0) = 1,即可得到文献[9–13]类似的结论.所以,本文进一步拓展了文献[9–13]在偏态数据的实际应用.
Pena 距离其向量形式定义如下

其中H=X(XTX)−1XT为帽子矩阵,p为对应解释变量的维数,exp(zTiˆγi)为删除第i个点后模型方差的估计值.ˆθi(j)则表示删除第j个数据点后第i个数据点的参数估计值.具体分析时,同样是先算出删除各点后某一点的Si,画出散点图,Si较大的则可能是异常点.
3 局部影响分析
局部影响分析是1986 年Cook 首次提出来的一种很有用的统计诊断方法,其主要思想是引入一个微小扰动(干扰)的概念,而把异常点或强影响点归结为“比其他点受到更大干扰的点”.若数据集中的一个或几个点比其他数据点受到的扰动大,则这个或这几个数据点就是异常点.
由文献[24]可知,将未受到干扰的模型(2)记为D,其扰动模型记为D(ω), ω=(ω1,ω2,··· ,ωn)T为刻画各样本点扰动大小的向量.对于受到扰动的模型,记其对数似然函数为L(θ/ω),参数的极大似然估计为ˆθω.另外,存在ω0=ω,使得D(ω0)=D,表示模型未受到扰动.
对于扰动模型D(ω)其似然距离定义为

上式的二阶近似表达式为
其中−¨F称为影响矩阵,表达式如下
其中∆是(p+q+r)×n阶矩阵,是n×n阶矩阵.
LD(ω)∗反映的是第i个样本点的扰动对极大似然估计的影响,其数值越大,就表示这个样本点对估计值的影响越大,如果存在某点j的扰动特别大,则这个点就是异常点.
最大特征向量法:LD(ω)∗关于方向d=ω−ω0的最大值,并设d=dmax时,LD(ω)∗达到最大值.dmax= (d1,d1,··· ,dn),并假设其中有一分量|dj|的值比其他分量大得多,则说明dj对于是的似然距离达到最大值做出了最大贡献,因而对应的数据点(yi,xi,zi,hi)即为异常点.因此,可作(i,|(dmax)i|)的散点图来找出异常点.
3.1 位置漂移扰动模型
位置漂移扰动模型如下

其中ω=(ω1,ω2,··· ,ωn)T, ω0=(0,0,··· ,0)T,表示模型没有扰动.θ=(βT,γT,αT)T,对应的对数似然函数表达示为
其中
L(θ|ω)的前二阶导数可表示为


3.2 尺度加权扰动模型
尺度加权扰动模型如下所示

其中ω=(ω1,ω2,··· ,ωn)T, ω0=(0,0,··· ,0)T,表示模型没有扰动.θ=(βT,γT,αT)T,对应的对数似然函数可表达示为
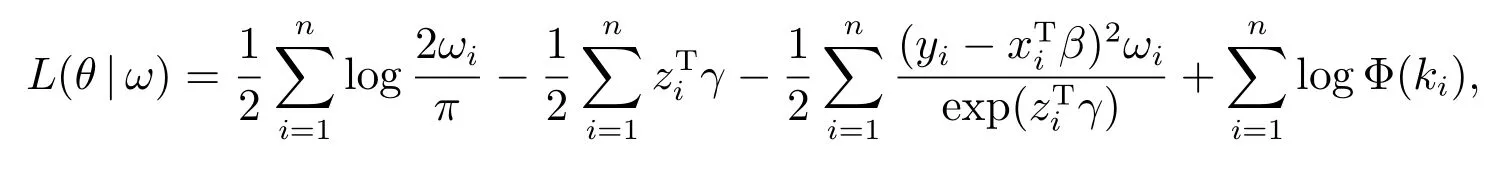
其中
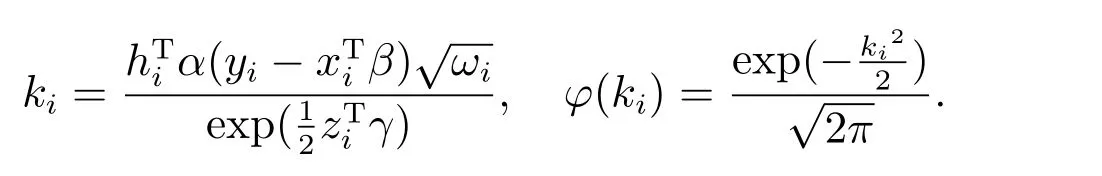
L(θ|ω)的前二阶导数可表示为

3.3 偏度加权扰动模型
偏度加权扰动模型如下
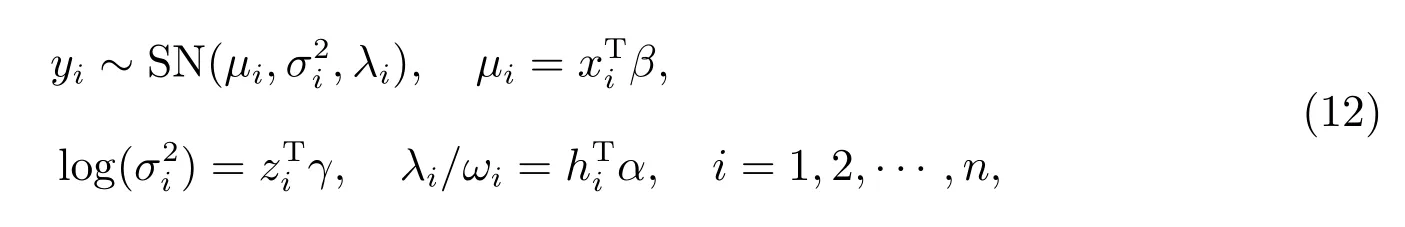
其中ω=(ω1,ω2,··· ,ωn)T, ω0=(0,0,··· ,0)T,表示模型没有扰动.θ=(βT,γT,αT)T,对应的对数似然函数可表达示为
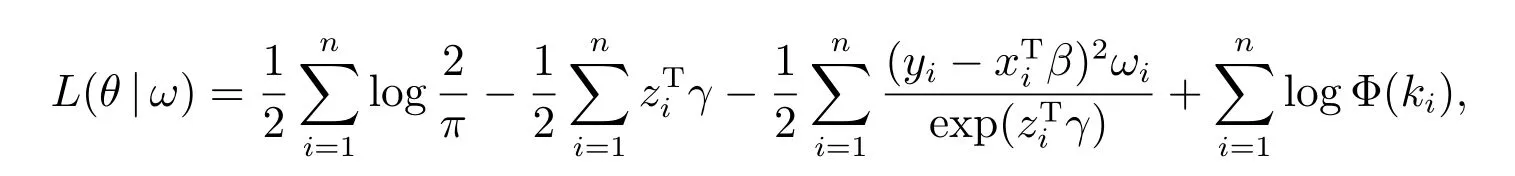
其中
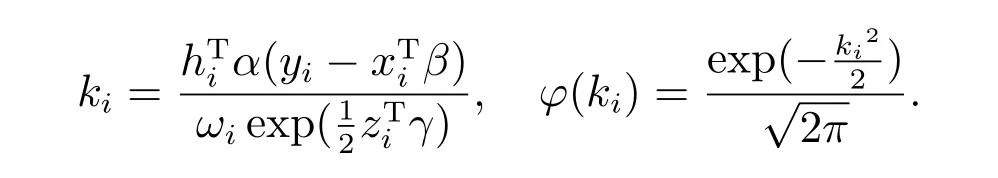
L(θ|ω)的前二阶导数可表示为
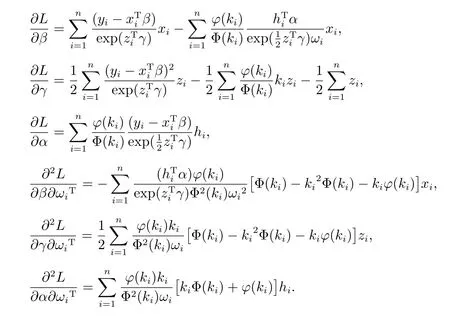
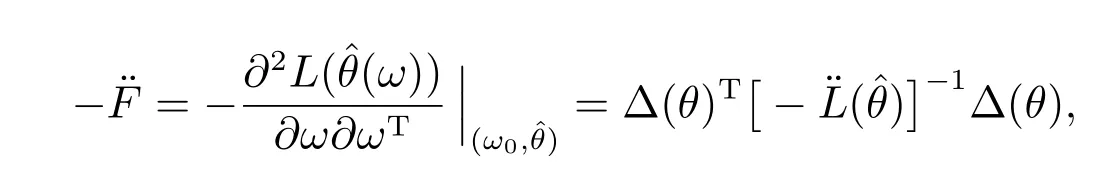
其中∆(θ)是(p+q+r)×n阶矩阵,是n×n阶矩阵.
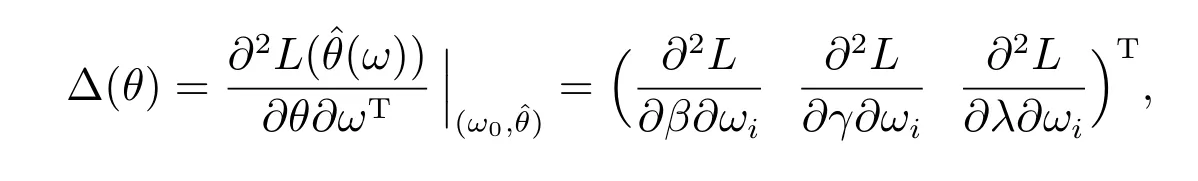
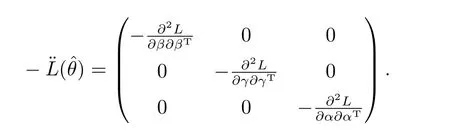
4 模拟研究及实例分析
4.1 模拟研究
为了检验本文提出方法的有效性,根据模型(2)我们产生随机数据,其中yi ∼SN(µi,,λi),xi, zi, hi均产生于U(−1,1), β, γ, α的真值分别取为(0.6,0.5,0.8)T,(1,2,−1)T,(2,0.8,−0.5)T,样本量n为200,并把38、132、180 号点设为异常点.然后根据上述的诊断方法得出模拟结果,模拟结果如图1 至图3 所示.

图1 样本量为200 时模拟数据的LD 散点图
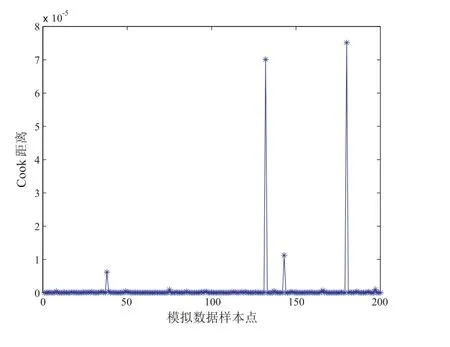
图2 样本量为200 时模拟数据的CD 散点图
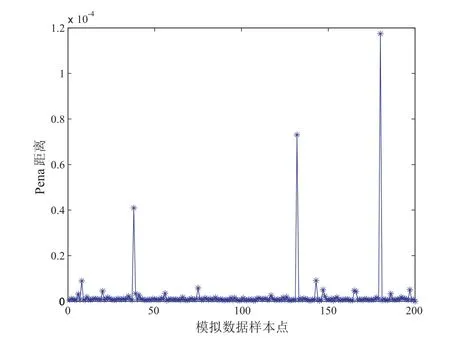
图3 样本量为200 时模拟数据的PD 散点图
从图中我们可以很清晰地看出38、132、180 号异常点均被诊断出来了,说明我们的方法是行之有效的.下面用实例进一步说明.
4.2 虹鳟鲑鱼数据[25]分析
鱼卵数量x和当年可捕捞成鱼数量y之间的关系,是养殖者非常关心的问题.下表1 所示是1940 年至1967 年在Skeener 河中红鳟鲑鱼的产卵量x和可捕捞的成鱼量y的测量数据.

表1 虹鳟鲑鱼数据
用QQ 图对虹鳟鲑鱼数据进行正态性检验,得到如下图4,利用Matlab 中的偏度函数skewness( )、峰度函数kurtosis( )得到实例数据的偏度为0.7063、峰度为3.0568,而正态分布的偏度值为0,峰度值为3.综合分析可知,虹鳟鲑鱼数据近似服从偏正态分布,可用本文研究的方法进行统计诊断.
考虑鱼卵数量x与可捕捞成鱼量y之间的联合位置、尺度、偏度模型,在该模型中xi, zi, hi完全相同,通过Matlab 计算得到完全数据下模型(2)的参数估计结果如下
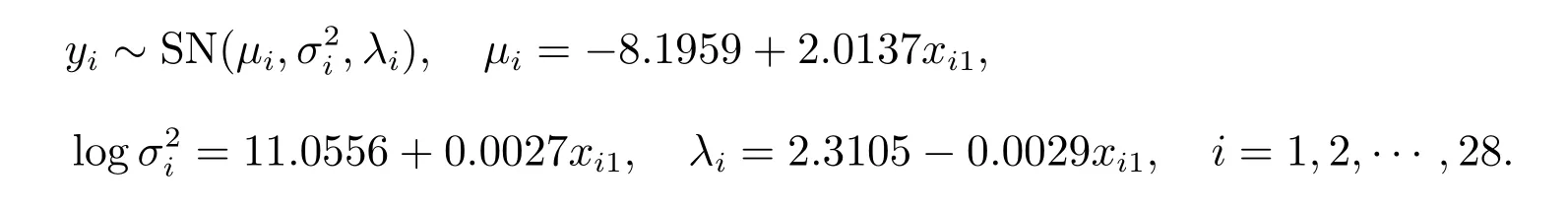
为了判断该数据集中哪些点是异常点,我们通过似然距离、Cook 距离、Pena 距离三种诊断统计量来诊断,诊断结果如图5 至图7 所示.
从图5 我们可以看出5、12、18、22、25 号点可能为异常点,从图6 可以看出12、18号点可能为异常点,而从图7 可以看出5、12、16、18 号点可能为异常点.由文献[24]统计诊断例6.4 可知5、12 号点为异常点,这是合理的,因为在原始数据中,第5、12 号点分别是被解释变量的最大值点和最小值点.而16、18 号点从表1 中我们也可以看出鱼卵量和可捕捞成鱼量与其他点明显异常.相较而言,Pena 距离诊断效果要比似然距离和Cook 距离要更精确一点.
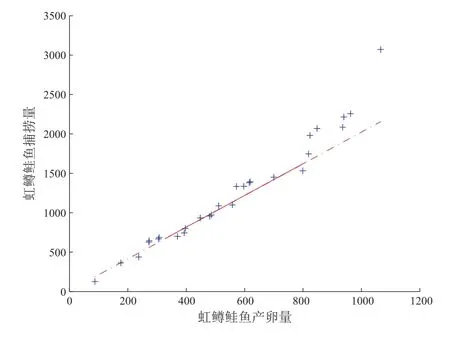
图4 虹鳟鲑鱼数据的正态性检验QQ 图
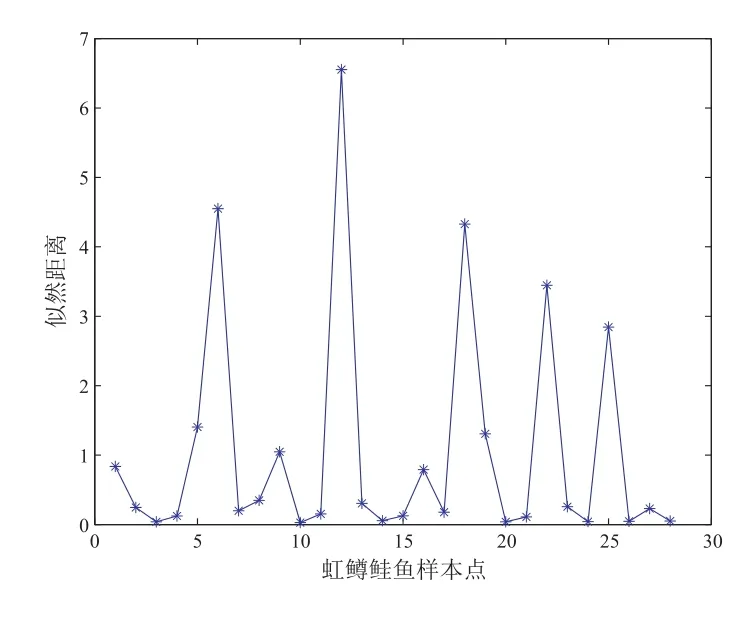
图5 虹鳟鲑鱼数据的LD 散点图

图6 虹鳟鲑鱼数据的CD 散点图
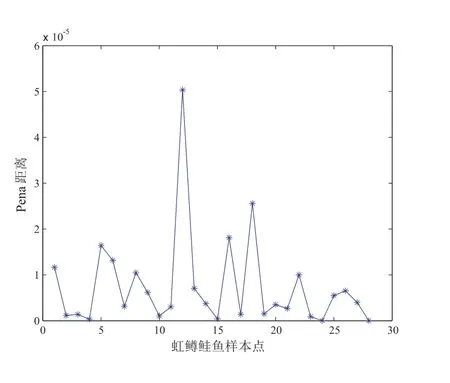
图7 虹鳟鲑鱼数据的PD 散点图
4.3 虹鳟鲑鱼数据的局部影响分析
采用位置漂移扰动、尺度加权扰动、偏度加权扰动三种方法对虹鳟鲑鱼数据进行诊断,通过计算得到如下图8 至图13 所示结果.
从图8 和图9 可以看出12 号点为强影响点或异常点;从图10 可以看出5、12、18 号点为异常点或强影响点,从图11 可以看出4、5、12、18 号点为强影响点或异常点;从图12、图13 可以看出12 号点为强影响点或异常点.而根据4.2 实例可知5、12、18 号点为异常点或强影响点,所以我们的局部影响分析中,尺度加权扰动模型的诊断效果比较好,位置漂移扰动模型和偏度加权扰动模型的效果略差一点.
5 结论
本文研究了偏正态数据的联合位置、尺度、偏度模型,将Pena 距离从正态推广到了偏正态,适用范围更广.利用Pena 距离、Cook 距离、似然距离以及局部影响分析进行诊断,得到了在一定条件下Pena 距离优于Cook 距离和似然距离.并做了局部影响分析,结果表明尺度加权模型的诊断效果较好,位置漂移扰动模型和偏度加权模型的效果略差一点.

图8 数据位置漂移扰动下−i(i)散点图
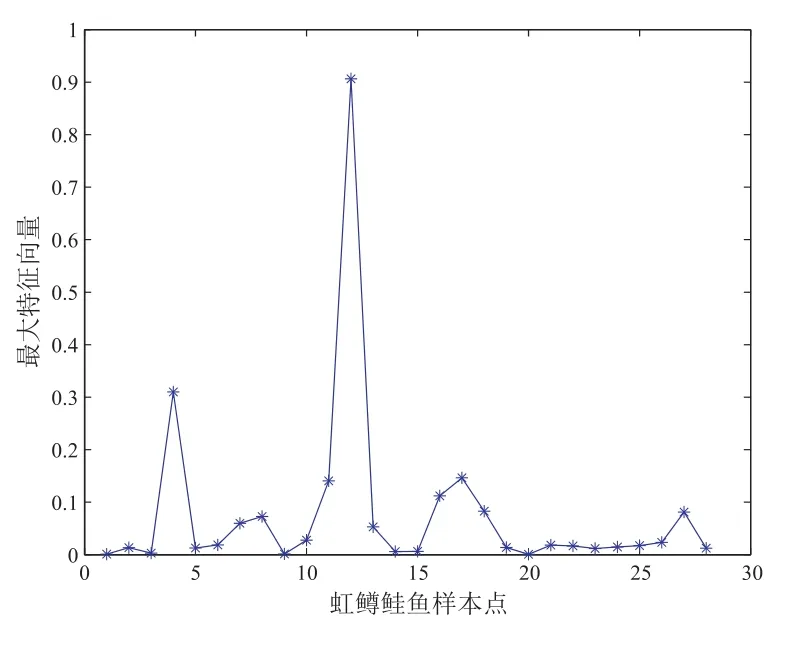
图9 数据位置漂移扰动下|(dmax)i|散点图
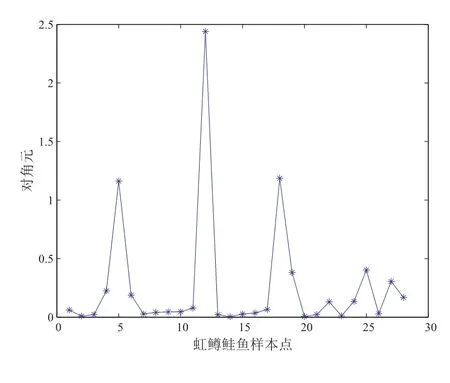
图10 数据尺度加权扰动下−i(i)散点图
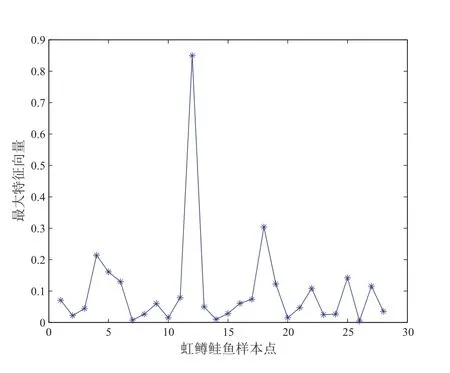
图11 数据尺度加权扰动下|(dmax)i|散点图

图12 数据偏度加权扰动下−(i)散点图

图13 数据偏度加权扰动下|(dmax)i|散点图
