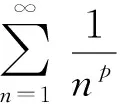p-级数余项的一个估计

周文书， 骆培业

(大连民族大学 理学院， 辽宁 大连116600)

1 引 言

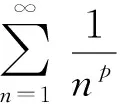
(1)

估计式(1)的重要意义在于它给出了余项Rk(p)收敛于零的一个速率.文[7]给出的估计式(1)的证明也相当初等，仅用到了如下不等式(见文[7]引理1)：

实际上，这个不等式可以被改进(见下文引理2).

基于这个不等式及Taylor展开公式，本文进一步改进了估计式(1)，得到了如下结果：

定理1设p为常数且p>1，则有

(2)

注1 定理1蕴含如下结果：

特别有

可见，定理1中结果是估计式(1)的一个改进.

注2 设p为常数且p>2.利用定理1可得到如下结果：

(3)

实际上，对估计式(2)两端同时求和，然后利用如下恒等式:

有

2 定理1的证明

定理1的证明基于如下两个引理.

引理1设p为常数且p>1，a，b是正数且满足a<1

证对任意x≥1，令

当x>1时， 有

因此，f(x)在(1，+∞)上是严格单调增加的，故f(x)>f(1). 证毕.

引理2设p为常数且p>1，则有

证令

则

对任意x∈(0，1)，由引理1知

故f′(x)>0，∀x∈(0，1)，于是

另一方面，由Taylor展开公式知

所以

证毕.

定理1的证明如下：

证对任意n∈，在引理2中取得

两边同乘以n1-p，得

上式两端同时关于n从k+1到+∞求和，得

证毕.

3 结 论

致谢感谢文献[7]给予本文的重要启示.