积分因子的一种直接求解方法

韩伟栋， 沈建和

(福建师范大学 数学与信息学院，福州350007)

1 引 言

可积性是微分方程和动力系统领域古老而重要的研究课题.微分方程的可积性，可用于揭示动力系统的轨道族及其分类，与物理的能量守恒、几何的等能量曲面和曲线等课题紧密相关.

积分因子和逆积分因子是可积性研究中的重要概念.欧拉曾试图用积分因子完全解决一阶常微分方程的求解问题[1].实际上，有关积分因子和逆积分因子的计算，至今仍是一个十分困难的问题.其原因众所周知：积分因子和逆积分因子的控制方程为偏微分方程，难以求解.所以，有关积分因子和逆积分因子的计算，通常要么针对具有特殊结构的微分方程，要么是求某些特殊形式的积分因子和逆积分因子.Cairó和Llibre[2]针对二维Lotka-Volterra(多项式)系统

研究了该系统的多项式首次积分和多项式逆积分因子的存在和计算问题.文献[3]针对形式如下的拟多项式常微分方程

研究了逆积分因子存在的充要条件，这里an(x)和bn(x)为连续可微函数.针对二维常微分方程组，文献[4]考虑具有更高维数的常微分方程组，给出了用于确定积分因子的偏微分方程组.文献[5-6]研究高阶线性常系数微分方程，给出了基于积分因子的求解方法，并与通常的特征值解法比较.文献[7]针对可分离变量的微分方程，分积分因子只与x或只与y有关两种的情况，讨论了积分因子的求解问题.

本文的目的是：通过有限次的变量替换并利用求导的链式法则，提出一种基于可分离变量微分方程的积分因子的直接求解方法.本方法的优点是：积分因子的求解，有直接计算的流程.具体而言，对于一阶常微分方程，只要其可以经过有限次的变量变换化为可分离变量的微分方程，那么它的积分因子和通积分，均可直接计算求出.

本文结构安排如下：第一节为引言；第二节给出可积性、积分因子、逆积分因子和变量分离微分方程等基本概念；第三节是本文的主要结论及其证明；最后一节是本文的结论.

2 基本概念

考虑一阶常微分方程

A(x，y)dx-B(x，y)dy=0，

(1)

或与之等价的二维向量场

(2)

定义1[9]称方程(1)、(2)为可积，如果存在区域D⊂×上的连续可微函数H(x，y)使得

DH(x，y)=Hx(x，y)B(x，y)+Hy(x，y)A(x，y)=0，

并称H(x，y)≡C为方程(1)、(2)的首次积分(通积分).

定义2[9]考虑区域D⊂×上的连续可微函数U(x，y)和H(x，y)，使得

DH(x，y)=U(x，y)A(x，y)dx-U(x，y)B(x，y)dy，

则称U(x，y)为积分因子，H(x，y)≡C为方程(1)、(2)的首次积分(通积分).

显然，积分因子U(x，y)满足如下偏微分方程：

(U(x，y)B(x，y))x=-(U(x，y)A(x，y))y，

即

U(Ay+Bx)+UyA+UxB=0.

定义3[8]考虑区域D⊂×上的连续可微函数V(x，y)(非零)和H(x，y)，使得

则称V(x，y)为逆积分因子，H(x，y)≡C为方程(1)、(2)的首次积分(通积分).

显然，逆积分因子V(x，y)满足如下偏微分方程：

V-1(Bx+Ay)=VxB+VyA.

定义4[9]形如

(3)

这里，f(x)和φ(y)分别是x和y的连续函数，称方程(3)为变量分离方程.

3 主要结果

定理1变量分离方程必然是恰当方程.

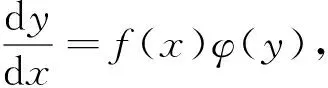
定理2若一阶常微分方程(1)可经非线性变量替换u=T(x，y)，化为变量分离方程

f(x)dx+g(u)du=0，

那么，积分因子U(x，y)可由下式确定

(4)

进而通积分同样可得.

证乘上非零的积分因子U(x，y)后，一阶常微分方程(1)变为

U(x，y)A(x，y)dx-U(x，y)B(x，y)dy=0，

(5)

此时，方程(5)已为恰当方程.

设引入如下的变量替换

u=T(x，y)，

(6)

将方程(1)化为变量分离微分方程

f(x)dx+g(u)du=0.

(7)

记方程(5)和(7)的首次积分(通积分)分别为H(x，y)和H(x，u)，那么有

Hy(x，y)=-U(x，y)B(x，y)，Hu(x，u)=g(u).

进一步地，利用求导的链式法则有

Hy(x，y)=Hu(x，u)uy|u=T(x，y)，

从而根据下式

可以求出积分因子U(x，y)，证毕.

注1 定理2的结果及其证明，均只涉及一次的变量替换；实际上，有限次的变量替换同样可得.

例1设函数f(u)和g(u)连续可微且f(u)≠g(u)，证明方程

yf(xy)dx+xg(xy)dy=0

(8)

有积分因子

证由定理2，记积分因子为U(x，y)，那么

yU(x，y)f(xy)dx+xU(x，y)g(xy)dy=0

已为恰当方程.

令u=T(x，y)=xy，在该变换之下，方程(8)可以化为

根据定理2的公式(4)知

即可得积分因子

例2当xM+yN≠0时，求齐次微分方程M(x，y)dx+N(x，y)dy=0的积分因子U(x，y).

证记积分因子为U(x，y)，那么

U(x，y)M(x，y)dx+U(x，y)N(x，y)dy=0

已为恰当方程.

另一方面，因为

令

则原方程可以化为

即

从而

根据定理2的公式(4)知

从而积分因子可直接计算得

例3如果M，N是m次齐次函数，则方程M(x，y)dx+N(x，y)dy=0的积分因子为

证记积分因子为U(x，y)，那么

U(x，y)M(x，y)dx+U(x，y)N(x，y)dy=0

已为恰当方程.

令

从而，原方程化为

M(x，ux)dx+N(x，ux)[udx+xdu]=[xmM(1，u)+uxmN(1，u)]dx+xm+1N(1，u)du=0.

两边同乘上

则方程可进一步转化为变量分离方程

因此

进而如下的积分因子可得

例4求解方程M(x)N(y)dx+P(x)Q(y)dy=0的积分因子U(x，y).

解设积分因子为U(x，y)，那么

U(x，y)M(x)N(y)dx+U(x，y)P(x)Q(y)dy=0

已为恰当方程.

另一方面，原方程可以化为

可得其通解

进而

从而积分因子为

例5求解方程x2y3dx+x4y3dy=0的积分因子U(x，y).

解设积分因子为U(x，y)，那么

U(x，y)x2y3dx+U(x，y)x4y3dy=0

已为恰当方程.

另一方面，令u=xy，从而原方程化为

此时，上述方程的通积分为

根据定理2的公式(4)知

从而积分因子为

4 结 论

(i) 本文针对一阶常微分方程，只要其通过有限次的变量替换可化为变量分离微分方程，笔者的方法均可以直接计算出积分因子，进而计算得到首次积分(通积分)；

(ii) 本文的方法，可以部分解决既跟x有关、又跟y有关的积分因子的求解问题(只要方程可通过有限次变量替换，化为变量分离微分方程)；

(iii) 最后指出的是：本文的方法具有可以直接计算的属性，非大量文献中的验证性的结果.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.