关于负超几何分布期望与方差算法的注记
2021-05-07王炳章
王炳章
(烟台大学 数学与信息科学学院,山东 烟台264005)
1 引 言
超几何分布是概率论中的一种典型的离散型分布,文献中有较多的讨论[1-3].本文将要研究的是教材中极少涉及的负超几何分布.在无放回抽样模型中,设n为产品总数而m为其中的次品数,则取到第r个次品时的抽取次数Xr的分布为
(1)
其中分布参数r;m,n都是正整数且满足1≤r≤m 于是,在有放回抽样中,取到第r个次品时的抽取次数即服从上述的帕斯卡分布(此时参数p=m/n). 文[6]中讨论的分布是本文(1)式当r=m时的特殊情况. 与帕斯卡分布类似,负超几何随机变量显然有一种通常的逐段分解方法.文[7]中利用负超几何随机变量的一种特殊的伯努利变量(0-1变量)分解法,算出了负超几何分布的期望与方差.但文[7]中给出的负超几何分布的形式比较复杂,不便导出其多维联合分布.本文首先讨论多个负超几何分布变量的联合分布及若干推论,最后利用联合分布的这些推论结合负超几何随机变量的通常的分解方法计算了负超几何分布的期望和方差. 设X1,X2,…,Xr分别为第1次、第2次、…、第r次取到次品时的抽取次数. 定理1设1≤i (2) 证利用文[8]中的不尽相异元素的排列模式,来确定m个次品的位置. 类似可以得到任意有限维的多维分布,从略. 推论1随机向量(X1,X2,…,Xr)的联合分布为 进一步,令 Y1=X1,Y2=X2-X1,Y3=X3-X2,…,Yr=Xr-Xr-1, (3) 从而得到负超几何变量Xr的通常的逐段分解式: Xr=Y1+Y2+…+Yr. (4) 每一段的变量Yi(1≤i≤r)是等待一个新的次品出现所需要进行的抽取次数,即是从第i-1个次品出现后到第i个次品出现所需要进行的抽取次数. 推论2随机向量(Y1,Y2,…,Yr)的联合分布为 证因为P(Y1=l1,Y2=l2,…,Yr=lr)=P(X1=l1,X2=l1+l2,…,Xr=l1+l2+…+lr), 由此根据推论1可看出欲证之式的正确性. 可以看出随机向量(Y1,Y2,…,Yr)的多维分布形式上是对称的. 推论3随机向量(Y1,Y2,…,Yr)的每个分量Yi(1≤i≤r)的分布为 (5) 即Y1,Y2,…,Yr服从相同的负超几何分布NH(1;m,n). 证利用引理1,根据求边缘分布的公式得 类似地,取r=2可得如下推论4. 推论4随机向量(Y1,Y2,…,Yr)的任何两个分量Yi,Yj(1≤i,j≤r)的联合分布为 (6) 定理2设随机变量Y服从负超几何分布NH(1;m,n), 则 证由Y~NH(1;m,n)得 有 故 进而有 E[(n+1-Y)(n+2-Y)] 即 于是有 因此 上式化简即可得到定理中D(Y)的表达式.定理2证毕. 结合推论3,对于i=1,2,…r, 有 (7) 定理3随机向量(Y1,Y2,…,Yr)的任何两个分量Yi,Yj(1≤i (8) 证利用推论4中Yi,Yj的联合分布,有 将(7)中第一式E(Yj)=E(Y)=(n+1)/(m+1)代入得 于是有 进而可求得 定理4对于(1)式中服从负超几何分布NH(r,m,n)的随机变量Xr,其数学期望和方差分别为 (9) 证利用负超几何变量Xr的分解式(4),有 例1某工厂的7件产品中有4件废品.作不放回抽样,设X为抽到第3件废品时的抽取次数.求X的数学期望和方差. 解 法一由(1)式得X的概率分布如下 P(X=3)=8/70, P(X=4)=18/70, P(X=5)=24/70, P(X=6)=20/70, 故 EX=(3·8+4·18+5·24+6·20)/70=4.8, 法二由题意知X~NH(r,m,n), 取n=7,m=4,r=3,代入(9)式得EX=4.8,D(X)=0.96. 直接计算的结果与本文理论结果完全一致. 注1 在总数为n而废品数为m的箱中作不放回抽样.抽取次数为r时抽到的废品数服从超几何分布H(r,m,n); 而取得r个废品时的抽取次数服从负超几何分布NH(r,m,n). 负超几何分布是不放回抽样模型中的一种等待时间分布,对其性质和数字特征的研究理论上具有重要意义,同时在统计推断中也具有一定的应用价值.本文首先给出了负超几何变量的联合分布,然后结合负超几何变量的一种自然的分解法,计算得出了负超几何分布的数学期望和方差.在教学过程中,适当的穿插类似这样的素材,对提高学生的创新能力有着积极的作用. 致谢感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.2 负超几何变量的联合分布及若干推论
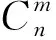
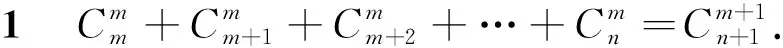
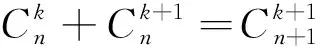
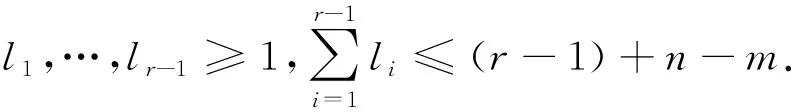
3 负超几何分布的期望与方差
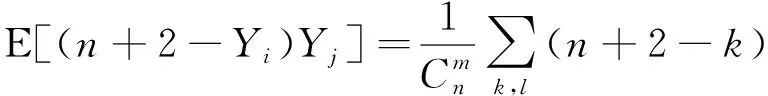
DX=(32·8+42·18+52·24+62·20)/70-4.82=0.96.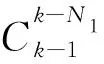
4 结 论
