渐近正态随机变量函数的极限分布

牛司丽， 刘玉晓

(1.同济大学 数学科学学院，上海200092； 2.河南城建学院 数理学院，河南 平顶山467036)

1 引 言

概率论在实际问题中具有非常广泛的应用，其中的中心极限定理更是概率论的杰出和经典工作，它为统计学的发展起着至关重要的作用. 这一理论结果的应用已广泛渗透至工程技术、经济金融、保险、医学、以及目前大家关注的人工智能和大数据分析等各个领域.

我们知道，在对未知量作统计推断时，常涉及到对其构造置信区间或作假设检验等，这必须利用相应估计量的分布. 在统计大样本理论的研究中，更多是研究估计量的相合性和渐近正态性等，相比来讲，研究渐近正态估计量函数的极限分布却少很多，但在实际应用中，常遇到讨论未知量函数的推断问题，由此就需要在知道该未知量的估计具有渐近正态性之后，研究它的函数对应的极限分布. 因此，在随机变量正态性应用的同时，渐近正态随机变量函数的极限分布也是非常重要的，本文对渐近正态随机变量函数的极限分布进行讨论，获得两个一般性理论结果. 作为应用，选取几个具体的函数，导出一系列渐近正态随机变量，获得一些耳目一新的结果，其中包括泊松随机变量平方根的渐近正态性，以及随机变量部分和在正则化常数是随机变量情况下的渐近正态性.

2 主要结果

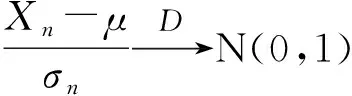
定理3设{Xn}是独立同分布的随机变量序列，如果Var(Xn)=σ2<∞，则当n→∞时，

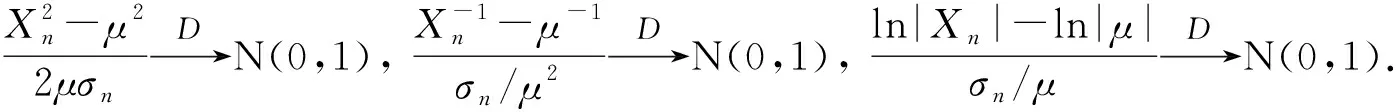
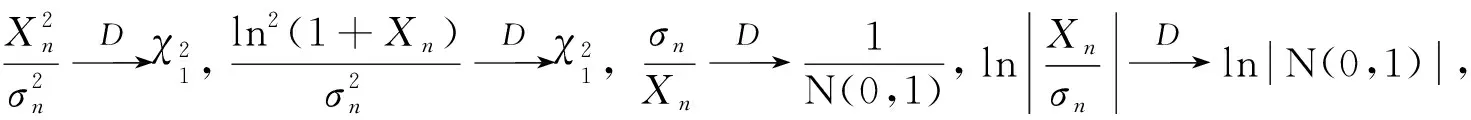
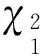
3 主要结果的证明

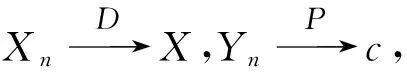
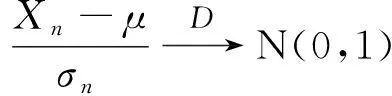
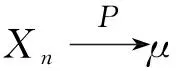
定理2的证明利用泰勒展开式，由假设当x→μ时，

定义

注意

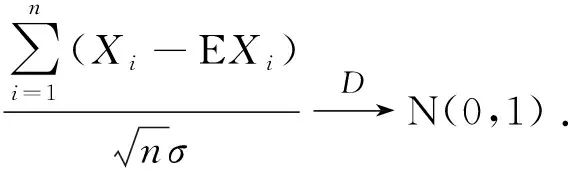
则应用引理1，当n→∞时

以及

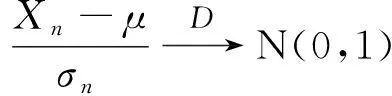
(iii) 令g(x)=ex，则g(x)是连续函数，并且对任意的μ，g′(μ)=eμ，于是应用定理1得到

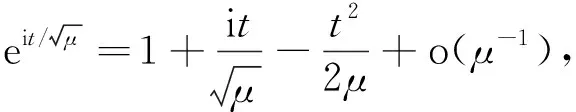
4 结 论

本文对渐近正态随机变量的函数，在定理1和定理2中分别建立两个一般性极限分布结果. 从例1和例2能够看到，利用建立的一般性结论能导出我们很少见到的一些耳目一新的结果. 另外，到目前为止，尚未看到涉及渐近正态自正则随机变量函数渐近分布更一般性的结论，后续对此可作进一步的讨论.

致谢作者感谢审稿人对本文提出的有价值的评论和修改建议.