正态总体均值置信区间长度的比较
2021-05-07石捡情刘继成刘显明
石捡情, 刘继成, 刘显明
(华中科技大学 数学与统计学院,武汉430074)
1 问题的提出
设X1,…,Xn为正态总体X~N(μ,σ2)的样本容量为n的简单随机样本,样本均值和样本方差分别记为
在总体方差σ2已知和未知两种情况下,总体期望μ的置信水平为1-α的置信区间分别是(文献[1]P194(7.10)和P196(7.13))
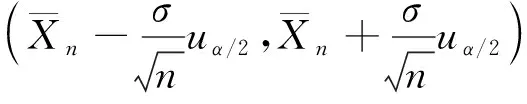
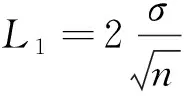
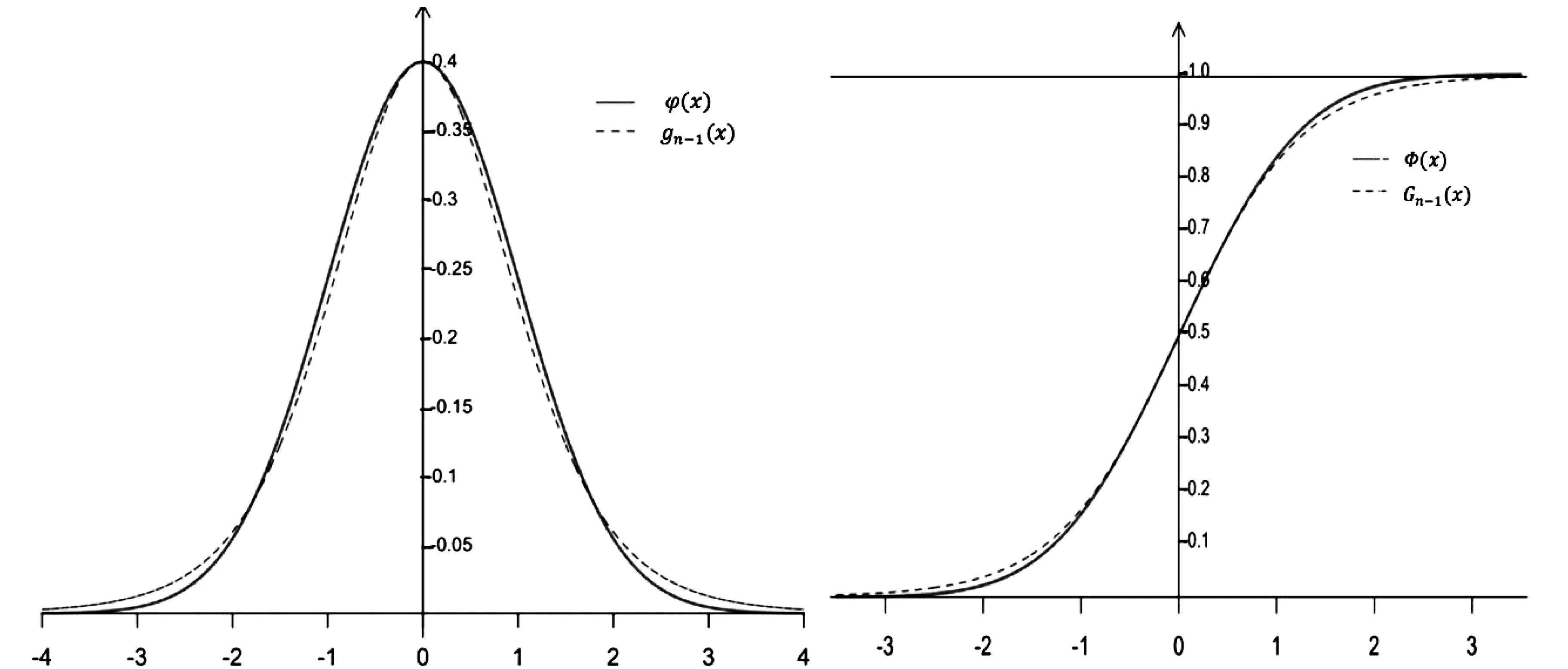
分析L1和L2的表达式,易知tα/2(n-1)>uα/2,通过Cauchy-Schwartz不等式得到E(Sn)<σ,文献[2]从数值上得出L1小于E(L2),本文的目的是严格证明L1 定理1对于任意n≥2,L1 为证定理1,只需等价证明σ·uα/2 回顾自由度为n-1的t分布的密度函数fn-1(x)和标准正态分布的密度函数φ(x) 对密度函数fn-1(x)在分位数下做变换,可得到另一概率密度函数记为gn-1(x),其上侧α/2分位数正是Cn·tα/2(n-1),最后通过探究概率密度函数φ(x)与gn-1(x)的图像交点问题来证明定理1成立.值得注意的是,为使E(Sn)的取值有意义,n的取值应不小于2,本文约定n≥2. 下面的引理来自文献[2],讨论了样本标准差Sn的数学期望和性质. ② E(Sn)关于n单调递增且收敛到σ. 文献[2]计算了E(Sn)的精确数值表示,且对E(Sn)的极限和单调性进行了计算与探讨. 由引理1中E(Sn)的表达式,记E(Sn)与σ的比值 (1) 即Cn是n的函数.E(Sn)单调递增且收敛到σ,则Cn关于n单调递增收敛到1.定义 (2) 下面的命题说明了gn-1(x)的性质. 命题1(i)gn-1(x)是一概率密度函数; (ii)Cn·tα/2(n-1)是概率密度函数gn-1(x)的上侧α/2分位点; (iii)gn-1(x)收敛到标准正态分布的概率密度函数φ(x); 证对自由度为n-1的t分布的概率密度函数fn-1(x)做积分变换. 根据式(1) 由上侧分位数的定义(文献[3], P131(2.7.5)),有 令x=Cn·t得到 (3) 即 取α=1,注意到tα/2(n-1)=0,有 (4) 即 (i) 易知gn-1(x)>0且为偶函数,由公式(4)可证gn-1(x)是一概率密度函数; (ii) 由公式(3)和上分位点的定义,Cn·tα/2(n-1)是概率密度函数gn-1(x)的上侧α/2分位点; (iii) 由于t分布收敛到φ(x),且当n→∞时, 已知Cn·tα/2(n-1)与uα/2分别是概率密度函数gn-1(x)与φ(x)的上侧α/2分位点,为此下面证明这两个函数图像在x正半轴只有一个交点. 命题2函数φ(x)与gn-1(x)在(0,+∞)上有唯一的交点.即存在K0,当x∈(0,K0),φ(x)>gn-1(x);当x∈(K0,+∞)时φ(x) 证原问题等价于方程φ(x)=gn-1(x)在(0,+∞)上有且仅有一个解.由对数函数的单调性,方程两边取对数化简,也等价于函数 在x正半轴有唯一零点. 首先证明函数m(x)在x正半轴至多有一个零点.对函数m(x)求导 记 下面证明函数m(x)在x轴正半轴有且只有一个零点.论文中,前面已经有下面符号和结论 因为 (5) 注意到m(0)=0,因此m(x)在x正半轴有且只有一个零点,函数φ(x)与gn-1(x)在(0,+∞)上只有一个交点,记为K0. 最后,比较gn-1(x)与φ(x)在(0,+∞)上的大小关系. 由于gn-1(x)与φ(x)在(0,+∞)均单调递减且在[0,+∞)上有且只有两个交点:0和K0,由式(5)知当x∈(0,K0)时,φ(x)>gn-1(x);当x∈(K0,+∞)时,φ(x) 下面来证明定理1. 概率密度函数gn-1(x)与φ(x)的累积分布函数分别记为Gn-1(x)与Φ(x),两者的概率密度函数图像和累积分布函数图像分别如图1和图2. 图1 概率密度函数图像 图2 累积分布函数图像 即 当x>0时,此时uα/2,Cn·tα/2(n-1)>0,Φ(x)>Gn-1(x),根据概率分布函数的单调性,所以有uα/2 定理1的等价形式得到了证明,因此定理1成立,即L1 本文证明了正态总体在方差已知和未知两种情况下,方差未知时的置信区间长度的期望要大.与直观一致,当方差σ已知时,关于正态总体可以利用的信息更多,更有利于区间的准确估计;当方差σ未知时,随着样本量的增多,样本中包含总体的信息增多,样本方差更加趋近于总体方差,两个置信区间估计精度的差别也越小.且当n→∞时,概率密度函数gn-1(x)趋于标准正态分布的概率密度函数,分位数Cn·tα/2(n-1)也将趋于uα/2. 另外,众所周知t分布是小样本分布,在n较小时与标准正态分布存在较大的区别,尤其是尾部概率要更大,tα/2(n-1)远大于uα/2.本文中得出的概率密度函数gn-1(x)是一个有趣的分布,比t分布更接近于标准正态分布,可以替代t分布来对小样本进行估计. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.2 分位数下的积分变换
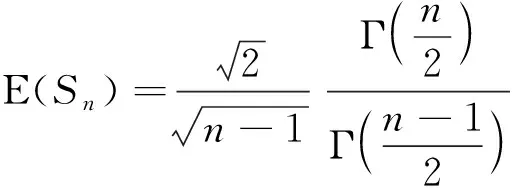
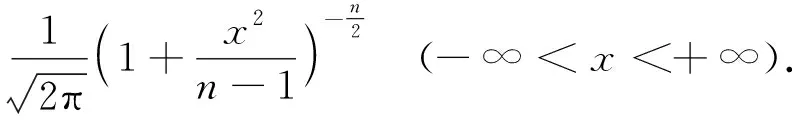
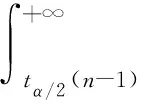
3 两个概率密度函数的比较
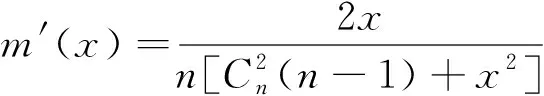
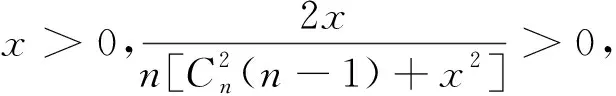
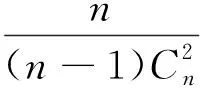
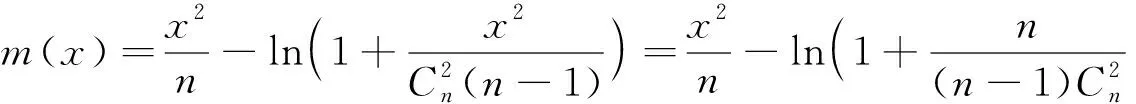
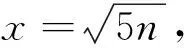
4 定理1的证明
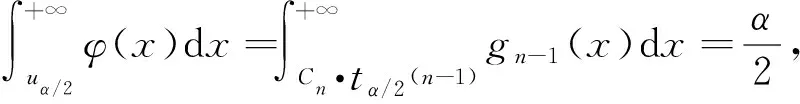
5 结 论
