广义τ-奇异模和τ-非奇异模*

李煜彦

（陇南师范高等专科学校数学系，甘肃陇南 742500）

0 引 言

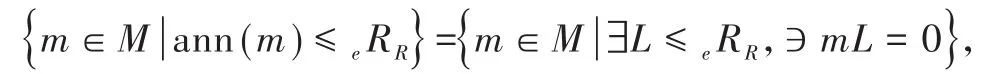
引理1［4］以下对M模成立.

（1）设N是M的非τ-挠子模.则N⊲τM当且仅当对任意 m∈Mτ(M)，存在r∈Rτ(R)，使得mr∈Nτ(N)；

（2）若N⊲τM，则对任意L≤M，都有N∩L⊲τN；

（3）若K⊲τK'≤M，L⊲τL'≤M，则 K∩L⊲τK'∩L'；

（5）设f：M→N是R-同态映射.若W⊲τN，则f-1(W)⊲τM.

引理2［6］设M是模，则以下结论成立.

（1）Zτ(M)是M是的子模；

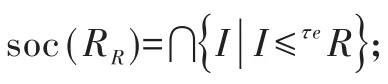
（3）设f：M→N是R-同态映射，则f(Zτ(M))⊆Zτ(N)；

（4）若N≤M，则Zτ(N)=N∩Zτ(M)；

（5）设 M=⊕i∈IMi，则 Zτ(M)=⊕i∈IZτ(Mi).

下面先给出Zτ(M)的性质.

性质1 设M是模，则以下结论成立.

（1）Zτ(M)是M是的子模；

（2）Zτ(M)⊆Z(M)⊆Zτ(M)，特别地，若 RR或M是τ-挠自由的，则Zτ(M)=Z(M)=Zτ(M)；

（3）若f：M→N是R-同态映射，则f(Zτ(M))⊆Zτ(N)；

（4）若N≤M，则Zτ(N)=N∩Zτ(M)；

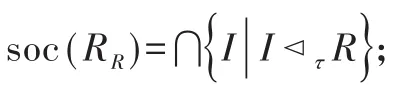
（6）设M=⊕i∈IMi，则 Zτ(M)=⊕i∈IZτ(Mi).

证明（1）设x，y∈Zτ(M)，r∈R.则存在 I⊲τRR，J⊲τRR，使得xI=0，yJ=0.由引理 1（3）知，I∩J⊲τRR，且 (x+y)(I∩J)=0.因此，x+y∈Zτ(M).同理可证xr∈Zτ(M).从而Zτ(M)是M是的子模.

（2）由文献［4］性质 2.1知，N≤eM当且仅当N⊲τM和 N≤τ-pM，故 Z(M)⊆Zτ(M).由文献［6］知，Zτ(M)=Z(M)∩τ(M)，故 Zτ(M)⊆Z(M).从而Zτ(M)⊆Z(M)⊆Zτ(M).

特别地，若RR或M是τ-挠自由的，则RR的广义τ-本质右理想和本质右理想以及M的广义τ-本质子模和本质子模都是一致的，故Zτ(M)=Z(M)=Zτ(M).

（3）设 x∈f(Zτ(M))，则存在m∈Zτ(M)，使得f(m)=x.于是存在 I⊲τRR，使得mI=0.因此，f(mI)=f(m)I=xI=0，从而 x∈Zτ(N).即 f(Zτ(M))⊆Zτ(N).

（4）显然.

（5）设 x∈Zτ(M)，则 ann(x)⊲τRR.故soc(RR)⊆ann(x)，从而 xsoc(RR)=0.

（6）设(mi)i∈I∈Zτ(M)，则 ann((mi)i∈I)⊲τRR.于是对任意 i∈I，ann(mi)⊲τRR.因此 (mi)i∈I∈Zτ(Mi)，即Zτ(M)⊆⊕i∈IZτ(Mi).反过来，设 (mi)i∈I∈⊕i∈IZτ(Mi)，则任意 i∈I，ann(mi)⊲τRR.则存在I的有限子集J，使得只有当i∈J 时，mi≠0.由引理 1（3）知，ann((mi)i∈I)=∩i∈Jann(mi)i⊲τRR.从而(mi)i∈I∈Zτ(M).

定义1 设M是模.称Zτ(M)为M的广义τ-奇异子模.若 Zτ(M)=M（或 Zτ(M)=0），则称 M是广义τ-奇异（或非奇异）的.

易知，Zτ是左正和预根.由文献［4］知，由广义τ-奇异模构成的类关于子模、商模、直和是封闭的；由广义τ-非奇异模构成的类关于子模、本质扩张、模扩张、直积是封闭的.

由性质1易得如下结论.

推论1 以下对模M成立.

（1）若M是广义τ-非奇异的，则M是非奇异的；

（2）若M是奇异的，则M是广义τ-奇异的.

定理1 模M是广义τ-非奇异的，当且仅当对任意广义τ-奇异模N，都有Hom(N，M)=0.

证明 必要性.设M是广义τ-非奇异的，N是广义τ-奇异的，f：N→ M是R-模同态映射.则由性质1，f(N)=f(Zτ(N))⊆Zτ(M)=0.

充分性.设对任意广义τ-奇异模N，都有Hom(N，M)=0.因 为 Zτ(Zτ(M))=Zτ(M)，所 以Hom(Zτ(M)，M)=0.特别地，对于包含同态映射 g：Zτ(M)→ M，g=0.从而Zτ(M)=0.

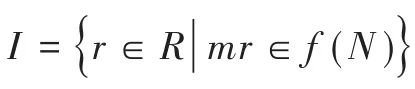
定理3 若L是τ-挠自由且广义τ-奇异模，则存在短正和序列0→N→fM→g

L→0，使得Imf⊲τM.

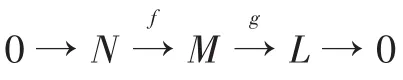
推论2 设L是τ-挠自由且广义τ-奇异模，f：R→L是R-同态映射.则Kerf⊲τR.

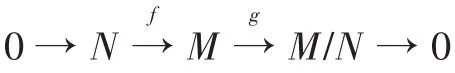
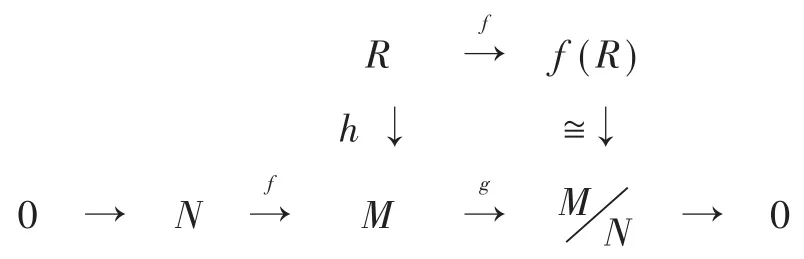
图1 交换图

由引理 1（5）知，kerf=h-1(N)⊲τR.

推论3 设M是广义τ-非奇异的，N≤M.则M/N是广义τ-奇异的当且仅当N⊲τM.

证明 必要性.若M/N是广义τ-奇异的，设m∈Mτ(M).显然m≠0，且存在 I⊲τRR，使得mI+N=N.下面说明mR∩N≠0，否则若 mR∩N=0，则mI∩N=0，且(mI+N)/N ≅(mI∩N)/mI.从而由正合序列0→mI∩N→mI→ (mI+N)/N→0可知，mI=0.于是m∈Zτ(M)=0，这与m ≠0矛盾.因此，存在r∈R，使得mr∈Nτ(M).从而由引理1（1），N ⊲τM.

充分性.由定理3易证.