基于悬链线理论的系泊系统的应用
2021-05-07项婷婷王国栋
项婷婷,王国栋
(安徽建筑大学 数理学院,合肥 230601)
0 引 言
海洋中蕴含着大量丰富的石油和天然气资源。随着我国燃油汽车保有量的持续增长,燃油资源的需求量日益剧增,对于海洋资源开发工作的技术要求将会越来越高。海洋资源的开发主要依托浮式平台,系泊系统的设计就是为了保证在资源开发过程中结构物和平台系统的安全。近年来,王磊[1]依据单点系泊系统动力学,利用集中质量法建立系统的静力学和动力学算法。王帅[2]根据耦合方程的系泊系统浮动区域状态,建立海上系泊系统的耦合方程,求解海上浮动区域的倾斜角度,吃水深度和浮动区域范围。Russell[3]等运用悬链线法对系泊系统进行了静力分析,将计算问题转化成方程求解,可用计算机快速处理。上述学者主要从力学理论角度分析系泊系统的整体情况,对不同环境下系泊系统重物球的研究较少。基于此,本文主要以浅水环境下的系泊系统[4]为研究对象,利用系泊系统的静力学分析方法[5], 对悬链线系泊系统浮标与系统间、系统内部不同材质连接处分别进行受力分析并构建算法。根据实例中环境条件和各部件参数得到浮标状态和锚链形状,并结合恶劣环境的临界条件和角度的限制条件,得到重物球设计方案。
1 实例分析
1.1 问题介绍
本文主要研究较浅海域的悬链式系泊系统。[6]系泊系统是指通过缆绳或其他机械装置将水面结构设施与固定点连接,使系泊结构物具有抵御一定环境条件的能力,保证在极端海况条件下,结构物和系泊系统的作业需求和安全。系泊线外形是由锚链和钢缆多个部分组成的弯曲悬链线。其中锚链与海床水平相接,近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成。
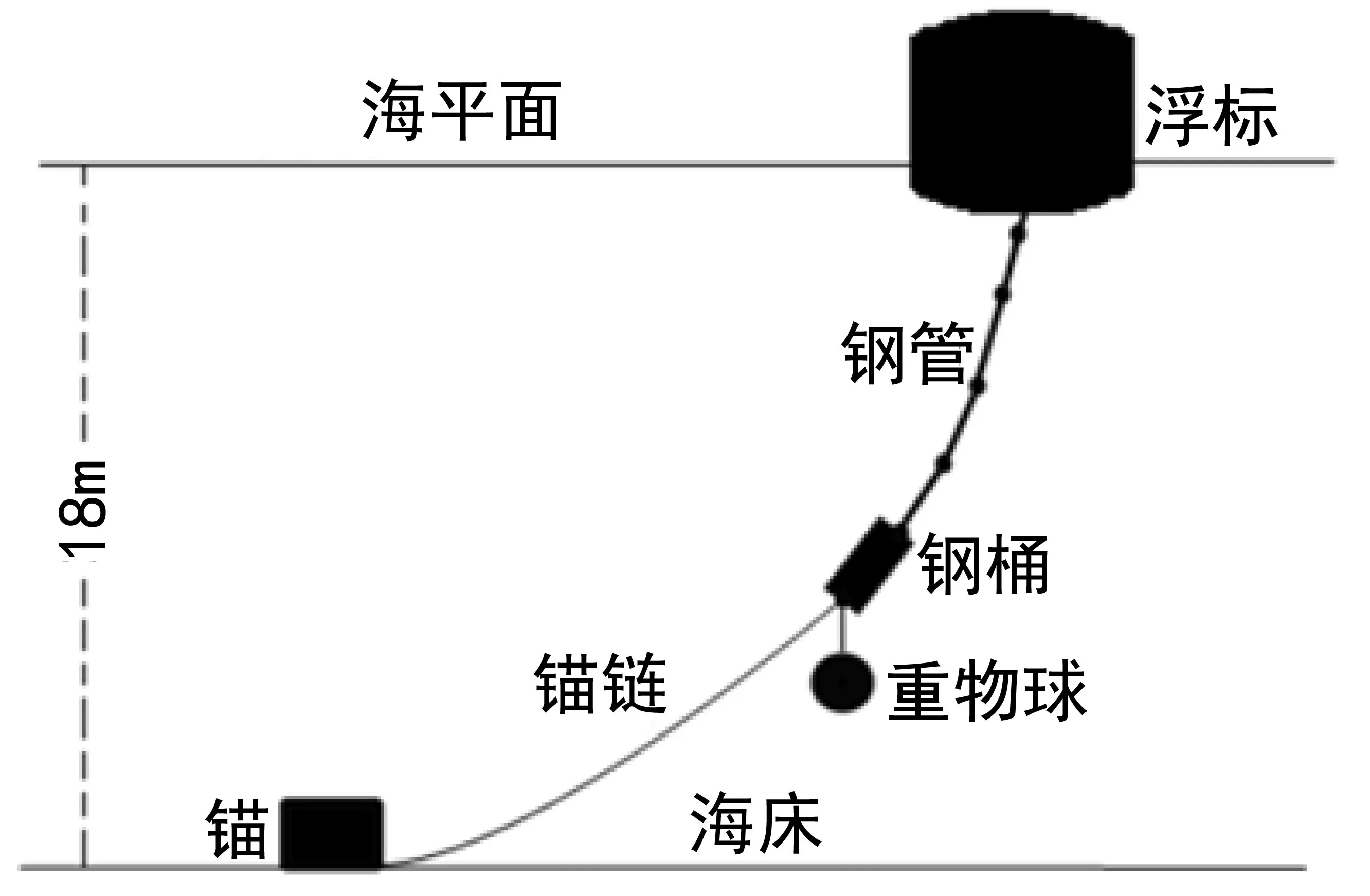
图1 传输节点图
问题1:传输节点如图1所示,海面风速24m/s,锚链长度22.05m,浮标质量1 000kg,直径长为2m。钢桶100kg,直径长为1m。钢管10kg,直径长为4m,重物球1 200kg。求浮标吃水深度、游动范围、钢桶倾斜角、四节钢管倾斜角和锚链形状。
问题2:接问题1条件,计算重物球质量范围。尽可能减小钢桶倾斜角度和浮标吃水深度,使钢桶角≤5,锚与海床角≤16。
1.2 问题分析
通过传输节点各部分间的受力分析和刚性物体与弹性物体的受力分析,构建方程组,分三步构建悬链线式系泊动力系统算法。首先,根据竖直方向的受力分析,以海水深度为18m为突破口试图建立受力守恒方程。进而,将锚泊系统分成三个算法,列出三个部分竖直方向高度守恒方程。最后,把三个算法整合为锚泊动力系统算法,算法建立流程如图2所示。

图2 算法建立流程图
由算法算出锚链刚被拉起的临界风速,针对问题一,对比临界风速,发现锚链刚好不离开海床,角度为0,算出未知参数值,用双曲余弦函数确定锚链形状。针对问题二,分析锚临界条件,使锚刚好离开海床,系统达到平衡。根据钢桶倾斜角度和浮标吃水深度临界值调控重物球范围。
1.3 问题假设与符号说明
1.3.1 问题的假设
1)由于浮标吃水深度变化幅度不大,因此本文假设浮标受风力面积近似算作定值;
2)忽略锚链、重力球体积,不计算浮力;
3)假设海面风速方向水平,且在水平面上任意方向的分析方法相同;
4)系统各段连接光滑,无阻力,g取9.8N/kg;
1.3.2 符号说明
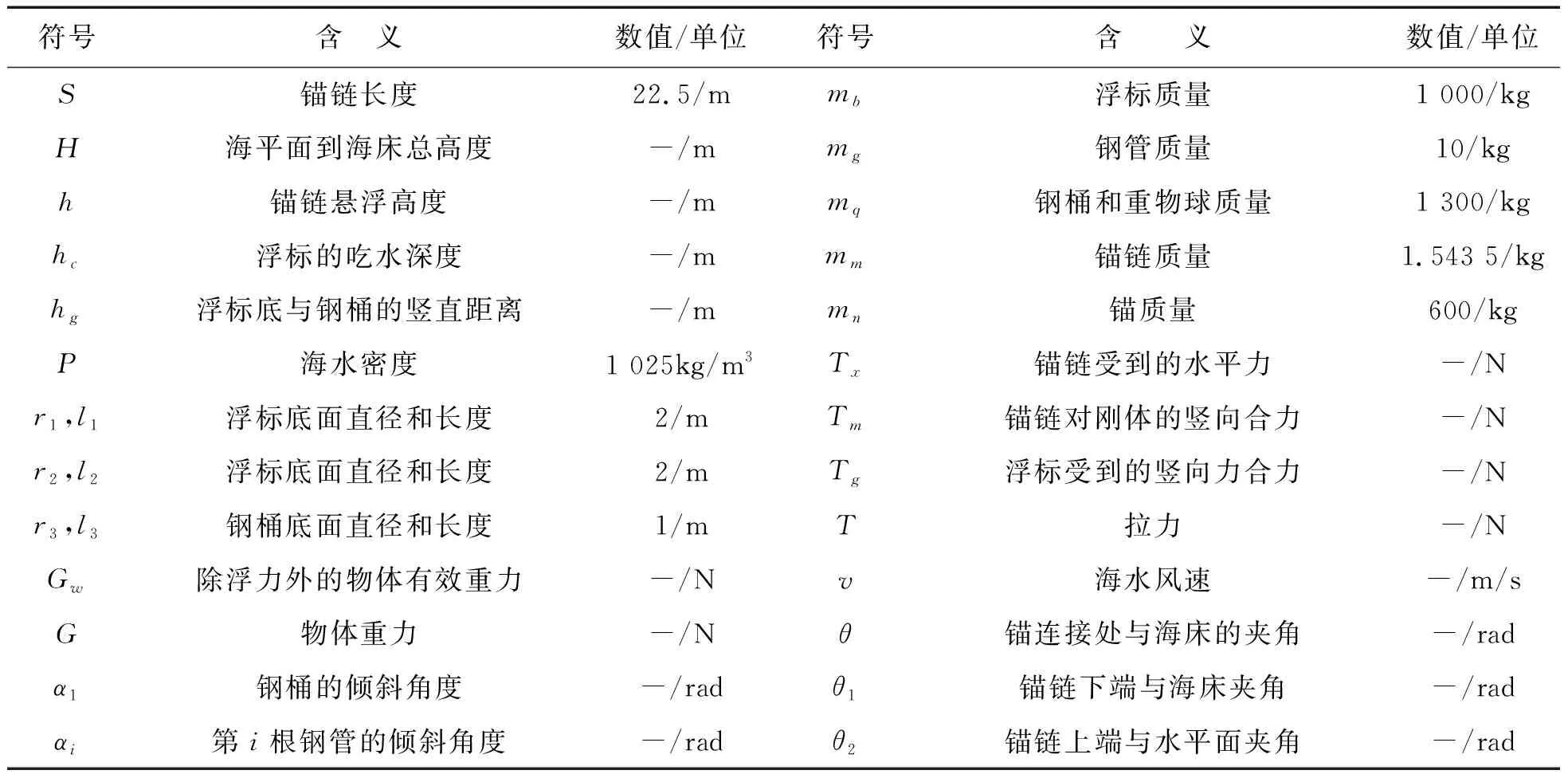
表1 符号说明表
2 系泊系统算法的建立及求解
本文讨论的是单点系泊系统,采用悬链线系泊方式和重力锚。由于连接锚与浮标的物质分布不均匀,因此涉及到弹性物体与刚性物体不同的力的传递方式,最终归结为传输节点各部分间的受力分析。对刚性物体和弹性物体进行受力分析,得到材质连接处力的传递大小与方向。以海水深度为18m为突破口建立动力守恒方程,分别对浮标、刚体和锚链三个系统受力分析,得到锚泊系统受力平衡方程组。
2.1 受力分析:
2.1.1 整体受力分析
如图3所示,在水平方向只受风力时,该系统任一点上的水平分力都等于该风力。而竖直方向上各部分的受力分析则比较复杂,故分两个供需系统进行受力分析。

2.1.2 供应锚链系统
供应系统由锚来提供横向力,重物球质量的改变是调节两个牵引的形状,保证锚提供最大的水平力。图中所示力从左到右分别为锚对锚链的拉力F、锚与锚链对刚体的竖向拉力Tm、供应系统对浮标的竖向拉力Tg。输出力分析如下图4所示。
2.1.3 需求浮标系统
水平方向,浮标为锚链提供牵引力T。竖直方向有悬浮的竖向力U,由浮力的改变承担。受力分析如图5所示。
2.2 锚泊动力系统
2.2.1 锚链受力分析
分析悬链式锚链非线性效应,用悬链线理论及状态方程式简化问题,求得锚链力。从几何上说,锚链在两端固定的自然状态称作悬链线,是一种双曲余弦曲线。端点受力如下图6所示。
其中:S为锚链长,Tx为水平方向所受外力,x为悬浮锚链水平距离,h为锚链水中高,Gw为锚链浮重。当θ1=0时,根据受力平衡与积分性质可得:
(1)
由双曲余弦曲线性质计算可得:
(2)
(3)
(4)
(5)
将式 (4)、式(5)带入式(1)、式(2)中,整理可得:
(6)
(7)
由式(1),式(6),式(7)可知同一悬链式上任意两个点之间受力和位置距离的关系:
Gx=Tx(tanθ2-tanθ1)
(8)
(9)
(10)
其中w=(m-pV)g/S为单位长浮重。
2.2.2 锚链和整体受力分析
由图3、图5可得浮标竖直受力:
(11)
由图4可得整体水深高度:H=hc+hg+h
(12)
综上可求得风向法平面投影面积S≈0.728(m2)。利用近海风载荷计算方法,得到风力风速转换公式:
F=0.625×Sv2(N)
(13)
2.2.3 刚性连接受力分析
如图7所示,钢管与钢桶竖直方向受力平衡满足:Txtanαi=Txtanαi-1+Gwi
(14)
其中:αi为第i个刚体水平夹角,Gwi为第i个刚体浮重度。在浮标上竖直方向的合力
Tg=Txtanαk=Txtanθ2+Gw1+…+Gwk
(15)
(16)
其中:Si为刚体长度。

图7 刚体受力分析
(17)
(18)
综合上述方程,可得锚泊动力系统算法:
(19)
2.3 问题求解
问题一
1) 角度临界条件分析(锚链切线角为零时的最大风速)
当锚链刚好不离开海床时,左端水平夹角为θ1=0,由式(13)、式(19)可得v≈24.310 550 3(m/s)。当锚链刚好离开海床时,左端水平夹角为θ1=16,同理求得v≈34.203 594 19(m/s)。
2) 问题一的解答
(1) 浮标吃水深度、游动半径、钢桶倾斜角。通过角度临界条件分析可知,当风速为24(m/s)时锚链没离开海床。依据所给数据,输入:v≈24(m/s),θ1=0。根据算法计算出悬浮水中的锚链长为:S24≈21.855 685 13(m)。
通过锚泊动力系统算法,结合MATLAB程序输出可得:系泊系统的吃水深度为0.749 2(m),游动半径为17.266 9(m)。钢桶竖直方向夹角为3.872 98(rad),由下往上的四根钢管与竖直方向夹角分别为:0.996 7(rad),0.991 0(rad),0.985 2(rad)和0.979 5(rad)。
(2) 锚链形状的计算
根据悬链线方程及性质[7],锚链形状可用双曲余弦函数表示:
其中α为缩放因子。由式(19)和MATLAB编程可得:α=13.346 7,水平距离x=16.933 1(m),悬浮高度,h=12.262(m)拖地长度为0.194 314 869(m)。锚链形状如图8所示。
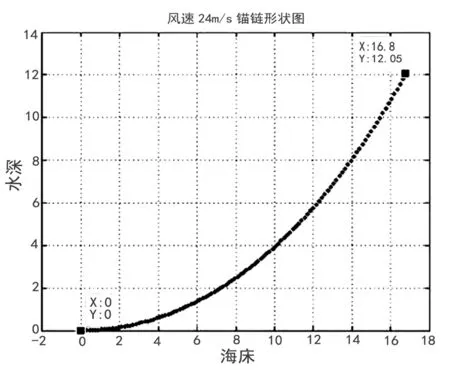
图8 风速24m/s锚链形状图
问题二
由算法可得,临界值θ1=16,θ=5下的重物球质量分别为2 111.228 491kg和2 763.371 348kg。浮标刚完全浸入海平面时,重物球为:5 303.768 252kg,所以重物球质量范围是:2 763~530 3kg.
3 总 结
1) 本文以浅海系泊系统为研究对象,根据锚链、浮标、刚体和整体受力平衡,提出悬链线式锚泊动力系统算法。该算法可计算在不同风力下系泊系统的吃水深度、浮标游动半径、重物球重量、钢桶倾斜角、刚体倾斜角、锚链悬浮高度和水平距离等参数。并结合悬链线性质拟合出锚链形状。
2) 根据锚链是否离开海床求出临界风速值,判断给定风速下的系统状态,并根据算法计算出重物球的质量变化范围,使系统最优。
3) 该算法可应用于带有悬链线和刚体的系泊系统,对单点系泊及类似系统观测网运作提供一定的参考与帮助。
