椭圆曲线y2=11nx(x2-32)的整数点

杜先存, 浦恩梅, 牛丽婷

(红河学院 教师教育学院, 云南 蒙自 661199)

椭圆曲线是20世纪最重要的数学理论之一,它是代数几何中最重要的一类研究对象,它的算术理论可以应用于公钥密码学.椭圆曲线的理论及其应用作为现代数论中的一个分支学科,可以说是集纯粹性、优美性、挑战性、应用性、实用性为一体的一个“突出例子”。由此可见研究椭圆曲线的整数点问题有着非常重要的意义.关于椭圆曲线y2=px(x2-a),p,a∈+的整数点,目前已有一些结果,主要集中在a=1,2,4,8,16,32,64,128上.a=1时,文献[1-2]已给出了一些相关的研究;a=2时,文献[3-5]已给出了一些相关的研究;a=4时,文献[6]已给出了一些相关的研究;a=8时,文献[7-8]已给出了一些相关的研究;a=16时,文献[9]已给出了一些相关的研究;a=32时,文献[10-11]已给出了一些相关的研究;a=64时,文献[12]已给出了一些相关的研究;a=128时,文献[13]已给出了一些相关的研究.a=32时目前的结论集中在p只含8k+5型素因子的情形,本文对a=32,p除了含8k+5型素因子外还含8k+3型素因子的情形进行研究.

1 定 理

n≡5(mod 8)为奇素数,椭圆曲线

y2=11nx(x2-32),

(1)

除(x,y)=(0,0)外无其他整数点.

2 证 明

显然(x,y)=(0,0)是椭圆曲线(1)的整数点,设(x,y)是椭圆曲线(1)的除(x,y)=(0,0)外的整数点.因为n是奇素数,所以由式(1)知11n|y,设y=11nz,z∈+,将其代入式(1)得

11nz2=x(x2-32).

(2)

因为gcd(x,x2-32)=gcd(x,32)=1或2或22或23或24或25,故方程(2)可以分解为以下4种情形:

情形Ⅰx=ka2,x2-32=11nkb2,z=kab,gcd(a,b)=1,a,b∈;

情形Ⅱx=kna2,x2-32=11kb2,z=kab,gcd(a,b)=1,a,b∈;

情形Ⅲx=11ka2,x2-32=nkb2,z=kab,gcd(a,b)=1,a,b∈;

情形Ⅳx=11kna2,x2-32=kb2,z=kab,gcd(a,b)=1,a,b∈.

其中k=1,2,22,23,24,25.

下面分别讨论4种情形下方程(2)的整数解的情况.

情形Ⅰx2-32=11nkb2两边取模n,得

x2≡32(modn).

(3)

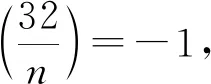
情形Ⅱx2-32=11kb2两边取模11,得

x2≡32(mod 11).

(4)

情形Ⅲx2-32=nkb2两边取模n,得

x2≡32(modn).

(5)

由情形Ⅰ的证明知情形Ⅲ不成立,则方程(2)无整数解,即椭圆曲线(1)除(x,y)=(0,0)外无其他整数点.

情形Ⅳ

(1)当k=1时,有x=11na2,x2-32=b2.将x=11na2代入x2-32=b2得121n2a4-32=b2,两边同时取模n得

b2≡-32(modn).

(6)

(2) 当k=2时,有x=22na2,x2-32=2b2.

将x=22na2代入x2-32=2b2得484n2a4-32=2b2,即

242n2a4-16=b2.

(7)

由式(7)可知b为偶数,设b=2c,c∈,将其代入式(7),得242n2a4-16=4c2,即

121n2a4-8=2c2.

(8)

又因为gcd(a,b)=1,则a为奇数,且n≡5(mod 8),即式(8)左边为奇数,右边为偶数,矛盾.因此k=2时,情形Ⅳ不成立,则此时方程(2)无整数解,即椭圆曲线(1)除(x,y)=(0,0)外无其他整数点.

(3) 当k=22时,有x=44na2,x2-32=4b2.

将x=44na2代入x2-32=4b2,得1 936n2a4-32=4b2,即

484n2a4-8=b2.

(9)

(4)k=23时,有x=88na2,x2-32=8b2.

将x=88na2代入x2-32=8b2得,7 744n2a4-32=8b2,即

968n2a4-4=b2.

(10)

(5)k=24时,有x=176na2,x2-32=16b2.

将x=176na2代入x2-32=16b2,得3 0976n2a4-32=16b2,即

1 936n2a4-2=b2.

(11)

(6)k=25时,有x=352na2,x2-32=32b2.

将x=352na2代入x2-32=32b2,得123 904n2a4-32=32b2,即

3 872n2a4-1=b2.

(12)

综上有情形Ⅳ不成立,即椭圆曲线(1)除(x,y)=(0,0)外无其他整数点.

综上所述,当n≡5(mod 8)为奇素数时,椭圆曲线(1)除(x,y)=(0,0)外无其他整数点.

定理得证.

3 结 论

利用初等数学方法证明了如果n≡5(mod 8)为奇素数,则椭圆曲线y2=11nx(x2-32)除(x,y)=(0,0)外无其他整数点.该研究结果对形如y2=px(x2-a),p,a∈+的椭圆曲线的求解有一定的借鉴作用,同时此结果推进了该类椭圆曲线的研究.