具有混合时滞的广义系统容许性条件
2021-05-07白雅迪
白雅迪, 孙 欣
(沈阳师范大学 数学与系统科学学院, 辽宁 沈阳 110034)
广义系统又被称作奇异系统、隐式系统或者微分代数系统[1].跟正常系统相比较,广义系统的形式更为广泛.广义系统常常出现在工程领域,例如电路建模与控制、电力系统、机器人系统和航空航天系统等[1].由于广义系统具有广泛的应用前景和深远的实际意义,引起了国内外众多学者的关注[2].时滞系统被定义为一处或者多处信号传递过程中出现时间延迟的动力系统.时滞的存在会给系统带来扰动,降低系统的性能,还有可能影响系统的稳定性.时滞几乎存在于所有的控制系统中,在测量元件的过程中以及执行元件和控制元件时都会产生时滞.
在得到广义时滞系统的稳定性条件之前,要保证广义时滞系统是正则的和无脉冲的,才能得到广义时滞系统的容许性条件.广义时滞系统的容许性研究一般采用Lyapunov-Krasovskii泛函方法.利用Lyapunov-Krasovskii泛函方法得到广义时滞系统的容许性条件大多是充分条件,所以会带来不同程度的保守性.因此有效地降低系统的保守性成为近年来研究广义时滞系统十分重要的课题.而广义时滞系统容许性条件的保守性与Lyapunov-Krasovskii泛函的构造和泛函求导后积分项的估计有关.如何通过构造合适Lyapunov-Krasovskii泛函来减少容许性条件的保守性成为重要问题.针对广义时滞系统的容许性条件,Liu[3]提出了松弛型Lyapunov-Krasovskii泛函,放宽了矩阵变量正定性的限制;Zhi等[4]构造泛函时,扩充了状态向量的维数,得到增广型Lyapunov-Krasovskii泛函;Kang等[5]在线性广义时变时滞系统的泛函中引入三重积分项,加入了更多的时滞信息.
广义时滞系统容许性条件的保守性也与Lyapunov-Krasovskii泛函求导后产生的积分项的估计有关.积分项估计常用的方法有模型变换法、Park不等式、Moon不等式、自由矩阵法和积分不等式法等.龚冠桦[6]应用Park双重积分不等式方法进行处理,得到了新的广义时滞系统稳定性的充分条件.Zhi等[4]提出二重积分自由矩阵不等式,并将其应用于广义时滞系统.Hien等[7]针对具有时变时滞和分布时滞广义系统,应用Jensen不等式得到了系统的指数稳定性条件.Seuret等[8]基于傅里叶理论提出了Wirtinger-based 积分不等式.对于Jensen不等式和Wirtinger-based 积分不等式,Zhang等[9]证明了使用无增广项的Lyapunov-Krasovskii泛函时,用Jensen不等式和Wirtinger-based 积分不等式得到的时滞系统稳定性条件是等价的,说明了构造合适增广型Lyapunov-Krasovskii泛函的重要性.Seuret等[10]提出了边界估值更为精确的Bessel-Legendre不等式,并且利用所提出的不等式得到时滞系统保守性更小的稳定性条件.由此启发,可以把Bessel-Legendre不等式推广到广义时滞系统,得到保守性更小的容许性条件.
本文针对具有混合时滞的广义系统,构造一种新的增广型Lyapunov-Krasovskii泛函,并在增广后的Lyapunov-Krasovskii泛函中加入了三重积分项.Lyapunov-Krasovskii泛函求导后产生的积分项使用保守性更小的Bessel-Legendre不等式进行放缩.得到的容许性条件以线性矩阵不等式的形式给出.数值算例说明了方法的优越性.
标记说明
1 问题描述
考虑具有混合时滞的广义系统

(1)
式中,x(t)∈n是系统状态向量;系统矩阵E∈n×n,且rank(E)=r≤n;A,Ad,AD∈n×n是已知的常数矩阵;常数时滞h满足约束条件h>0;φ(t)是连续可容的向量值初始函数.
定义1[11]
如果det(sE-A)≠0,那么称矩阵对(E,A)是正则的;如果degdet(sE-A)=rank(E),那么称矩阵对(E,A)是无脉冲的;如果det(sE-A)=0的根全部具有负实部,那么称矩阵对(E,A)是稳定的;如果矩阵对(E,A)是正则、无脉冲的、稳定的,那么称矩阵对(E,A)为容许的.
定义2[7]
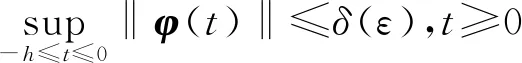
引理[10](Bessel-Legendre不等式) 对于矩阵R∈n×n,R>0,参数b>a,可微向量函数x:[a,b]→n,则以下不等式成立:

(2)
式中,

(3)
式中,
2 主要结果
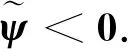
定理考虑混合时滞广义系统(1),对于标量常数h>0,若存在正定对称矩阵

式中
则具有混合时滞的广义系统(1)是容许的(*表示对应矩阵的转置矩阵).
证明 第一步证明具有混合时滞的广义系统(1)是正则、无脉冲的.
式(4)可以等价写成
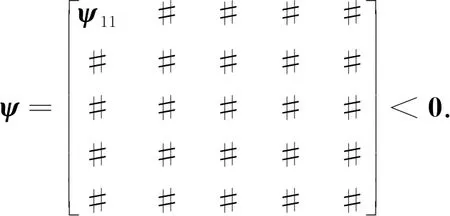
(5)
式中,
#表示和接下来的讨论过程无关的内容.
因为N,R,M是正定矩阵,所以它们的主子式大于零,即
N11>0,R11>0,R22>0.
并根据式(5)得到
因为rank(E)=r (7) 令 式中,L1∈(n-r)×(n-r)是非奇异矩阵. 式(8)的分块方式都与式(7)的分块方式一致. 式(6)分别左乘和右乘HT、H,得到 (10) 式中, 容易得到 Δ<0. (11) (12) 显而易见A22是非奇异的.假设A22是奇异的,那么一定存在一个非零向量φ∈n-r,使得A22φ=0.然后由合同变换得到 (13) (14) 令 又 令 (19) 式中, 由式(14)和式(18) 可以知道,具有混合时滞的广义系统(1)可以写成 (20) 即 (21) 不难看出系统(20)和系统(1)得到的稳定性条件是等价的.所以系统(20)如果是稳定的,那么系统(1)也将是稳定的.接下来证明系统(20)是稳定的. 构造增广型Lyapunov-Krasovskii泛函为 (22) 式中, 定义 应用引理,可以得到 由式(27)和式(28)得 整理得 (31) 式中, (33) 所以 (34) 根据李雅普诺夫第二方法,得到系统(20)是稳定的,所以系统(1)也是稳定的.因为系统(1)是正则的、无脉冲的和稳定的,所以具有混合时滞的广义系统(1)是容许的.证毕. (35) 推论考虑混合时滞系统(35).对于标量常数h>0,若存在正定对称矩阵P>0,P∈4n×4n,N>0,N∈3n×3n,M>0,M∈n×n,R>0,R∈3n×3n.满足线性矩阵不等式 式中, 则混合时滞系统(35)是稳定的. 例1 考虑如下具有混合时滞的广义系统: 式中, 表1 比较最大允许时滞上界Table 1 Comparisons of the maximum allowable upper bounds of delay 表1中比较了文献[6,13-14]和定理算出的系统最大允许时滞hM.例1的数值算例来自文献[6],并且使用MATLAB的LMI工具箱进行求解. 从表1可以很直观地看出,定理获得了比文献[6,13-14]更大的具有混合时滞的广义系统允许时滞上界,说明定理具有较小的保守性. 例2 考虑如下具有混合时滞系统 式中, 通过MATLAB的LMI工具箱求解,得到系统最大允许时滞hM=2.040 4,说明了所提出方法的有效性. 本文针对具有混合时滞的广义系统,从2个方面来减小系统容许性条件的保守性:一方面将二次项、一重积分项和二重积分项的状态向量增维,构造了新型的增广型Lyapunov-Krasovskii泛函;另一方面使用保守性更小的一重二阶Bessel-Legendre不等式和二重二阶Bessel-Legendre不等式,对Lyapunov-Krasovskii泛函求导后的积分项进行放缩,最后得到了具有混合时滞的广义系统保守性较小的容许性条件.将结论推广到具有混合时滞系统中,得到了具有混合时滞系统的一个新的稳定性条件,所用方法的可行性和优越性在数值算例中得以体现.所用方法还可以应用于连续广义时滞系统和定常时滞系统,能得到保守性更小的稳定性条件.


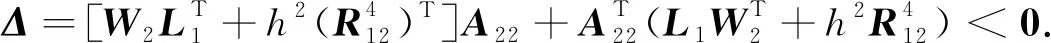



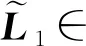
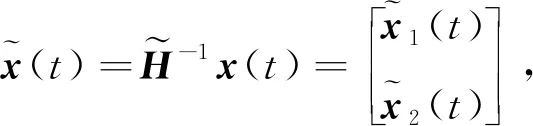

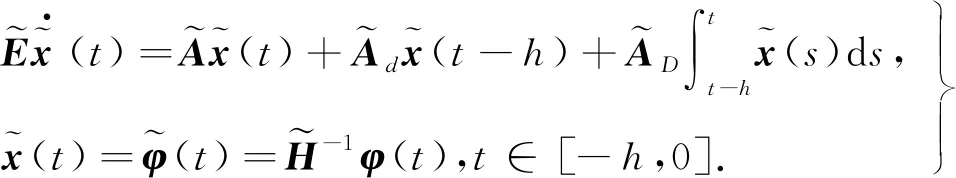







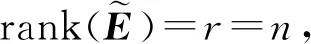

3 数值算例

4 结 论
