水-热耦合作用下严寒地区高速铁路隧道温度场分布规律

赵希望, 张 恒

(1.广东省隧道结构智能监控与维护企业重点实验室， 广州 511440； 2.中铁隧道局集团有限公司勘察设计研究院， 广州 511440； 3.华南理工大学土木与交通学院， 广州 510641)

寒冷地区隧道的修筑打破了围岩的原始热平衡，围岩中存在的水分会在寒季冻结成冰[1]。由于液相转为固相体积增大，进而使隧道衬砌背后围岩产生冻胀力；在暖季，冻结的冰融化成水，在冻结时产生的位移不能完全恢复，造成的空隙又会增加渗漏，严重时可能发生融陷，这种衬砌背后围岩的反复冻融作用使衬砌防水层发生破损，进而产生更大的冻害，造成衬砌结构变形，使隧道运营安全受到威胁[2-4]。

众多专家和学者对新疆、青海等严寒地区的隧道进行了研究。赖远明等[5]运用伽辽金法对青海大坂山隧道温度场和渗流场耦合非线性问题进行了分析和研究，通过无量纲分析法和摄动技术求出寒区圆形隧道温度场的解析解。高焱等[6]对寒区隧道洞内空气温度及围岩温度场进行了分析，给出了保温层的铺设范围。陈建勋等[7]首先结合寒区公路隧道防冻保温层的设计，对保温材料现场的保温性能进行了测试，确定了最佳的防冻保温材料组合和施工，然后运用正弦函数回归法对隧道拱顶、拱腰、边墙和路面四个部位实测的温度数据进行了分析。张学富等[8]根据青藏铁路昆仑山隧道内实测大气温度和围岩温度，考虑冰-水相变影响，应用伽辽金法推导了有限元公式，对昆仑山隧道施工期间融化的围岩进行了回冻预测研究，分析了隧道铺设保温材料和无保温材料的温度场，得出保温材料对多年冻土区隧道融化回冻过程所起的作用。郭春香等[9]以昆仑山隧道为例，利用有限元法分别计算了考虑混凝土水化热和不考虑混凝土水化热的隧道围岩融化回冻过程，分析了混凝土水化热对围岩融化、回冻过程的影响。杨旭等[10]基于围岩温度场现场测试的结果，同时考虑水文地质条件、混凝土水化热、大气温度和地温等因素，比较了季节冻土区隧道施加保温层和未施加保温层的冻融循环圈的差异。周元辅等[11-12]推导了多年冻土隧道隔热层的数学优化模型，分析了隔热层用于多年冻土隧道的合理性和经济性。从以上对寒区隧道的研究中可以看出，防冻保温层是寒区隧道防治冻害的有效措施，确定保温层铺设的合理性和经济性对寒区隧道工程有着重要的意义。但是，以上分析中或是以多年冻土区隧道施工期间造成的围岩融化为对象，研究衬砌背后围岩的回冻过程，并不适用于初始融土地区隧道修筑后，由于围岩热平衡破坏造成的衬砌背后围岩冻结的问题，如文献[8-9]；或是在隧道温度场的分析中只考虑了衬砌、围岩热传导，没有考虑水分迁移或冰水相变，如文献[10-12]。

针对融土地区隧道修筑后，衬砌背后围岩冻结的问题，以吉图珲客运专线榆树川隧道为依托，根据瞬态温度场问题的能量平衡方程和水分迁移方程，考虑水分迁移、冰-水相变等因素，建立了寒区隧道围岩水-热耦合模型，并结合现场实测大气温度，利用有限元法对严寒地区隧道温度场进行计算，比较有、无保温层对隧道温度的影响，确定隧道冻害发生的最不利位置和时间，分析保温材料对隧道冻融圈的影响，给出保温层厚度和导热系数的合理值。

1 水-热耦合作用下传热数学模型

1.1 温度场方程

土体在冻结时水蒸气蒸发耗热很少，考虑水分迁移和冰水相变，土体内发生的热传导[13]可以表示如下。

融化区:

(1)

冻结区:

(2)

式中：f、u为围岩冻结和融化状态；λ为热传导系数，W/(m·℃)；T为温度，℃；t为时间；c为围岩的比热容，J/(kg·℃)；ρ和ρi为分别为围岩的密度和冰的密度，kg/m3；L为单位质量冰水相变潜热，kJ/kg；θi为体积含冰量。

在冻结锋面位置处s(t)，应满足连续性条件

Tf[s(t),t]=Tu[s(t),t]=Tm

(3)

式(3)中：Tm为土体的冻结温度，℃。

1.2 水分场方程

根据文献[14-15]，土体内的空气和水蒸气在孔隙内的流动带动的水分迁移量相当微弱，因此，忽略空气和水蒸气迁移对水分的迁移的影响，冻结和融化过程中围岩内水分迁移满足Darcy定律，可表达为

(4)

式(4)中：K为导水系数，m/s；φ为基质势，Pa；θu为未冻水体积含量；ρw为水的密度，kg/m3。

根据徐斅祖等[16]的实验结果，未冻水含量θu与负温始终保持动态平衡的关系，即

θu=a1|T|-b1

(5)

式(5)中：a1和b1为与土质因素有关的经验常数。

1.3 温度场方程和水分场方程的耦合

土体中的微分水容量C(m-1)是等温条件下基质势与体积含水量θu之间的定量关系[16]，表达式为

(6)

土壤的水分扩散系数D可以表示为土体微分水容量C与导水系数K的关系[16]，即

(7)

Taylor等[17]认为未冻结土的土-水特征曲线也适用于冻结土的情况。因此，根据冻土中未冻水含量与温度的关系以及土-水特征曲线可确定不同温度的未冻水基质势，表达式为

(8)

综合式(2)、式(4)、式(6)～式(8)，土体冻结区的热传导方程可以表示为

(9)

用等效热传导系数λe和等效比热容Ce代替围岩融化和冻结状态的热传导系数λu、λf和比热容cu、cf，则考虑冰-水相变和水分迁移的围岩热传导方程可以表示为

(10)

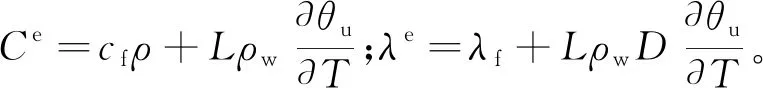
式(1)～式(10)组成了隧道围岩冻结过程中的水-热耦合模型，采用COMSOL Multiphysics 软件的PDE (partial differential equations)模块进行求解。以T和θ为因变量，得到两个广义型PDE标准形式为

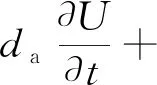
(11)

式(11)中：da为质量系数；U为微分方程因变量，U={T,θ}；Γ为通量向量；f为源项。

将节点温度T和含水量θ作为基本未知量，运用隐式欧拉向后差分(BDF)法对控制方程中的时间项进行离散，采用非线性迭代修正阻尼牛顿法求解方程。利用有限差分时间步长的方法，对该微分方程进行时间差分，并通过连续线性循环解法求解。

1.4 模型验证

为验证提出的水-热耦合模型的正确性，采用胡和平等[18]对于张掖壤土的冻结试验和结果进行数值模拟。胡和平等采用张掖壤土，在试验室内进行了一组单向冻结试验。试样的高度为13.68 cm，直径为11.36 cm。试样的初始温度如表1所示，试样的初始体积含水量为22.08%。冻结实验时，试样的侧面为热绝缘条件，顶部与底部温度按照如图1所示变化，试验在冻结2 830 min后结束，并将试样取出，然后将试样切片，在烤箱中烘干得到总含水量。

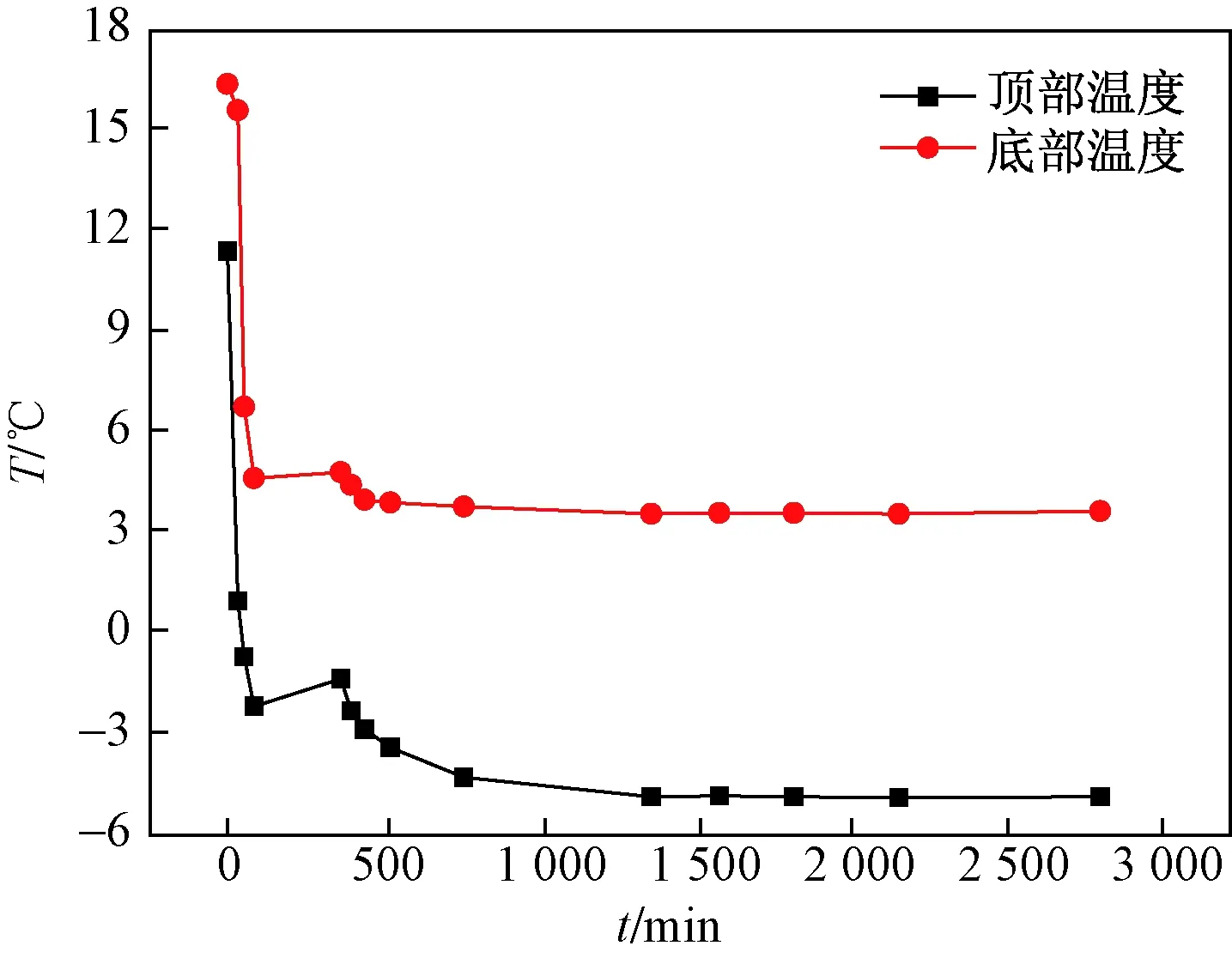
图1 试样顶部和底部温度变化Fig.1 Temperature variations at the top and bottom of the sample

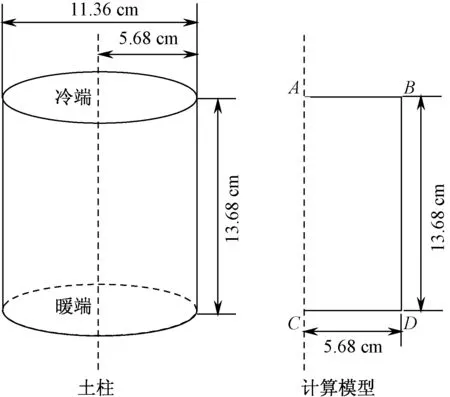
图2 计算模型Fig.2 Calculation model

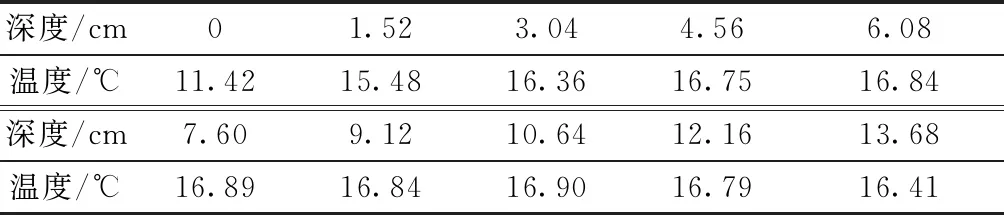
表1 试样初始温度分布

计算时，取轴对称计算模型(图2)，边界条件和初始条件如下：

温度边界条件：AC为对称边界；BD为绝缘边界；初始温度场沿深度方向按照表1分布。AB和CD边界温度随时间变化情况如图1所示。

渗流边界条件：AC为对称边界；AB、BD和CD都是不透水边界，即试样处于封闭环境中。

试验所用土为张掖壤土，热物理参数如表2所示。

表2 张掖壤土热物理参数

在土体冻结过程中，土体孔隙中生成的冰晶体会阻碍孔隙内水分的迁移孔道，从而导致水分扩散系数D和渗透系数K减小。受土体孔隙内冰晶体的影响，土体在冻结过程中的分水扩散系数D和渗透系数K[19]可以表示为

(12)

(13)

式中：I为阻抗系数；a2、b2、a3和b3分别为物理试验常数，其值如表3所示。

表3 张掖壤土物理参数

图3所示为试样在不同冻结时刻(34、528、2 830 min)，不同深度处温度实验值与计算值的比较。可以看出，各冻结时刻试样内温度的计算值和实验值能够很好地相吻合，这说明该水-热模型能够很好地模拟土体冻结过程中的温度分布规律。同时，可以看出：冻结初始阶段，试样处于正温状态，但随着冻结的进行，试样发生自上而下的冻结，冻结锋面不断下移。冻结初期温度传递速率较快，随冻结时间的增加温度传递速率逐渐减小，最终温度趋于稳定。

图3 不同时刻土样温度计算值与试验值的比较Fig.3 Comparison between the experimental and simulated temperatures of soil sample at different time

图4为实验结束时试样内含水量的计算值和实验值的比较，含水量的实验值和计算值在形状和分布特征上都是一致的。试验开始时，试样的初始含水量为22.08%，但试验结束时，试样内的最大含水量的实验值为29.2%，计算值为32.2%；最小值含水量的实验值为18.2%，计算值为18.4%，计算值与实验值非常接近，并且最大含水量位置的计算值和实验值也相当吻合。这说明水-热模型可以很好地模拟土体冻结过程中的水分迁移现象。

图5为在不同冻结时刻(100、528、2 830 min)，试样不同深度处的含冰量分布。可以看出，在冻结过程中试样发生自上而下的冻结，试样含冰量随时间的变化也表现出冻结初期主要分布在土体浅层，随着冻结的进行，冰向土体内部不断增长，在冻结锋面位置处含冰量达到最大。由于在实验中土体含冰量的变化无法进行测量，在实验结束后测得的都是液态水的含量，所以对土柱在冻结过程中冰含量的分布和变化的分析是一个难题。水-热耦合模型可以实现对土体在冻结过程中冰含量变化的监测，为分析土体内冰的分布和含量提供了方便。

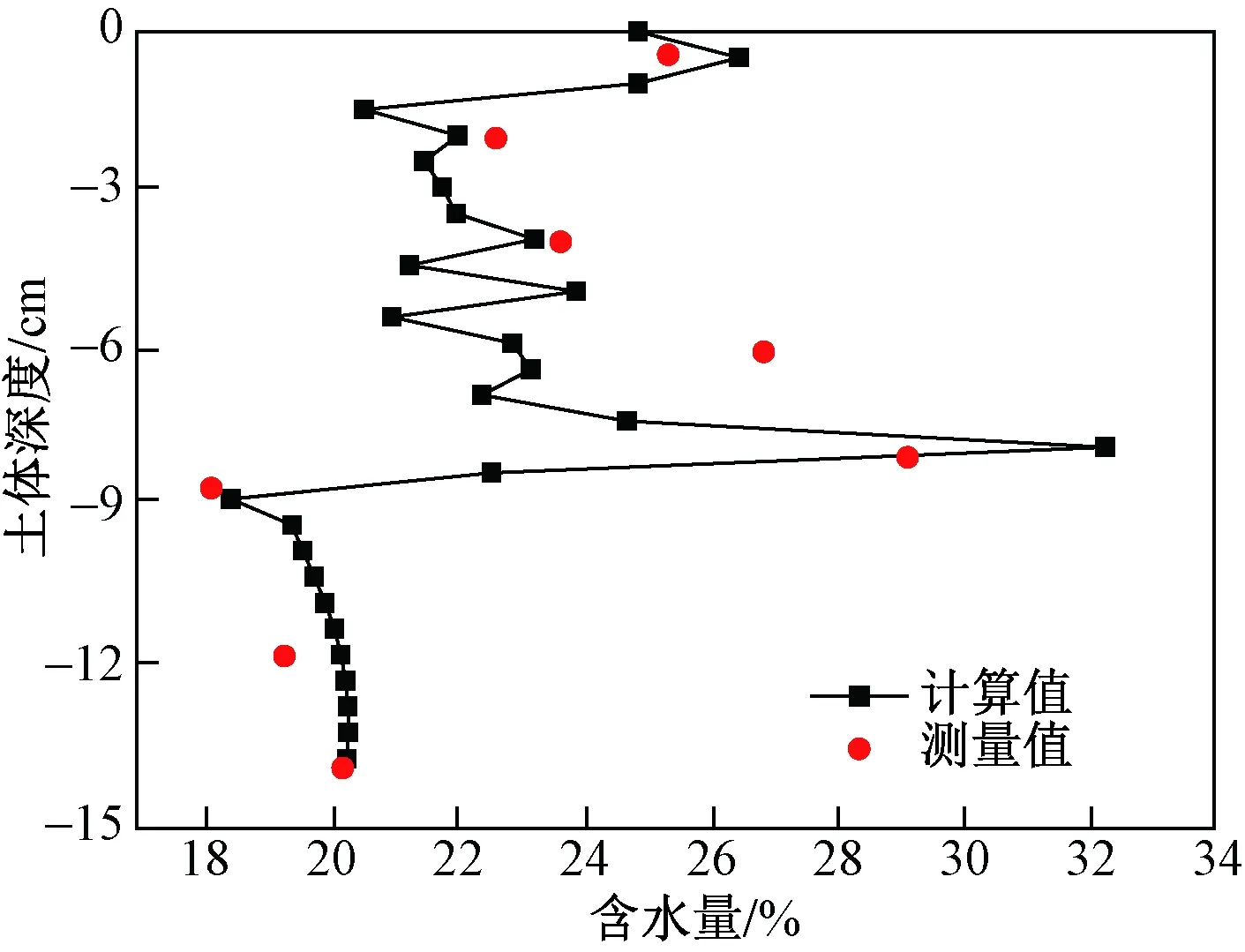
图4 实验结束时土样含水量的计算值和实验值的比较Fig.4 Comparison between the experimental and simulated water content of soil sample at the end of experiment

图5 不同时刻土体含冰量的计算值Fig.5 The calculated ice content of soil sample at different time

2 数值模拟

2.1 工程概况

新建吉图珲客运专线位于吉林省东部吉林市和延边朝鲜族自治州境内，线路全长360 km，设计时速250 km/h，其中，榆树川隧道进口位于延吉市安图县境内附近，隧道全长2 210 m，最大埋深约160 m，如图6所示。根据延吉市地区气象资料和水文地质条件，隧址年平均气温5.32 ℃，极端最高气温37.7 ℃，极端最低气温-29.2 ℃，最冷月平均气温-16.5 ℃，最大冻结深度为1.68 m。隧道进口处大气月平均温度如图7所示。

图6 榆树川隧道照片Fig.6 Photo of the Yushuchuan tunnel

图7 隧道外大气温度Fig.7 Air temperature outside the tunnel

根据水文地质条件，榆树川隧道通过地层为强风化、全风化砂岩。隧道开挖后，地层之间的热平衡被打破，隧道的进口和出口处因受到大气温度的作用，在冷季围岩中的水分发生冻结，从而使隧道衬砌发生冻胀破坏。

2.2 有限元模型

考虑到隧道纵向长度较长，计算断面位于榆树川隧道里程DK273+704处，该位置距离隧道进口30 m，隧道内空气温度可取为大气温度[15]。计算模型宽AD=BC=60 m，高AB=CD=80 m，隧道埋深15 m，计算模型如图8所示，围岩和衬砌的热力学参数见表4。

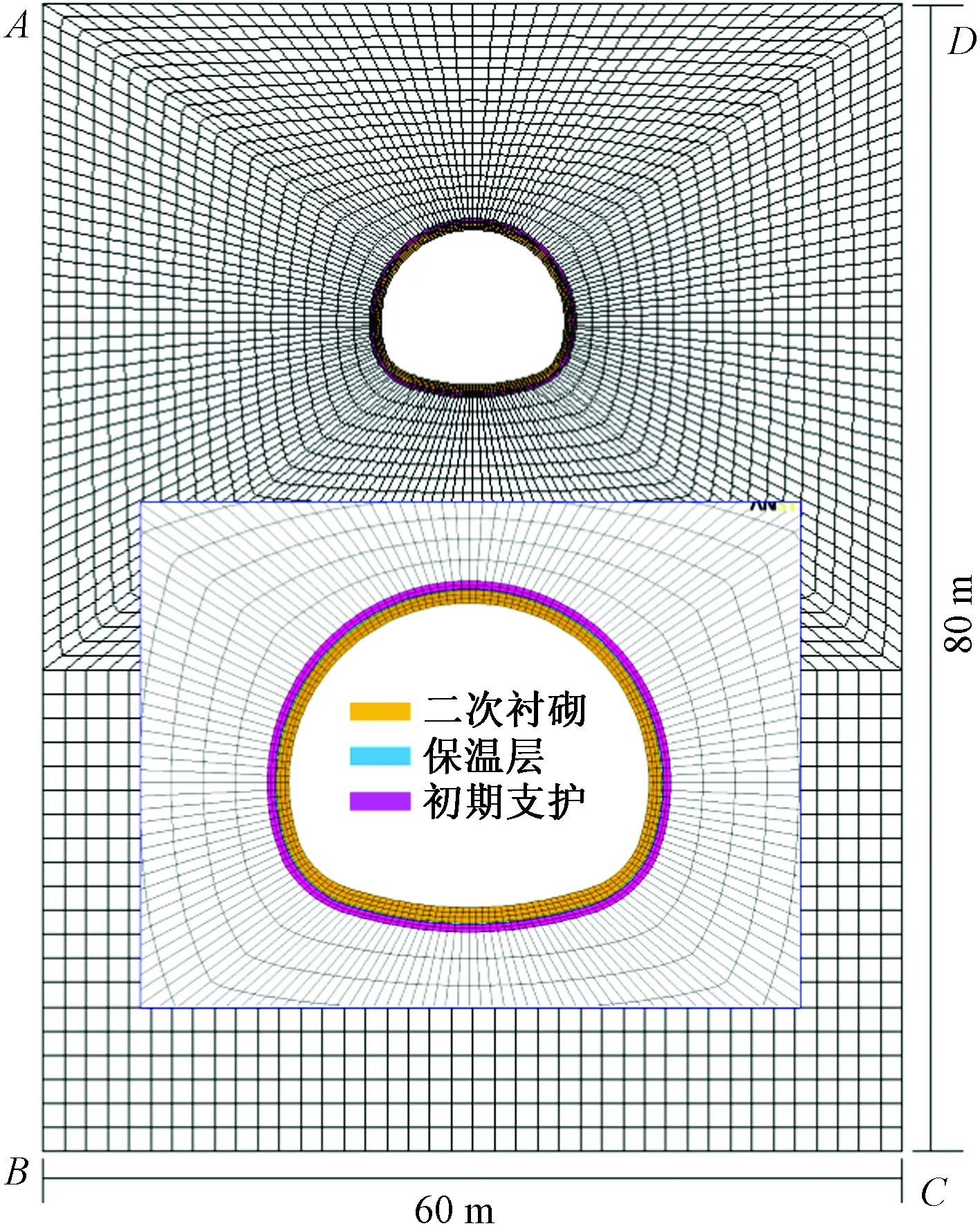
图8 隧道计算模型Fig.8 Numerical model of the tunnel

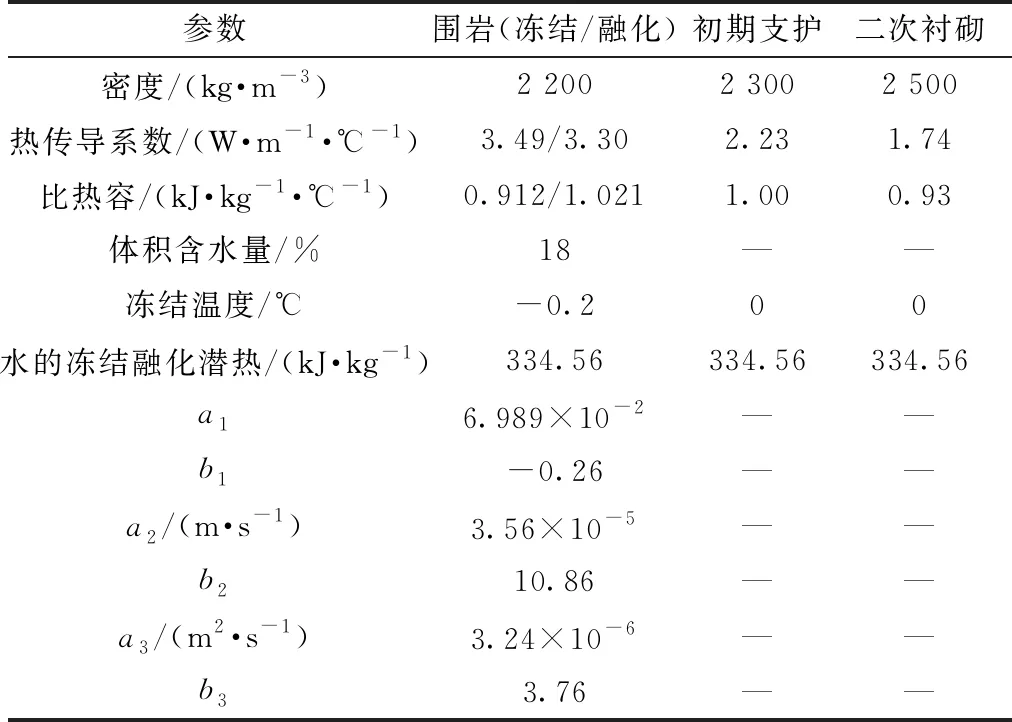
表4 围岩和衬砌热力学参数

2.3 边界条件

温度边界：模型AB和CD为绝热边界；隧道衬砌边界与隧道内空气对流换热，对流换热系数为12.5 W/(m2·℃)。模型底部BC的热流密度为0.01 W/m2。

水分边界：考虑到隧道顶部的植被会减弱降雨和降雪对围岩含水量的影响，同时在初期支护与二次衬砌之间施做防水层，因此，模型AB、BC、CD和AD边界均为不透水边界。

3 计算结果与分析

3.1 无保温材料隧道温度场分布

在隧道运营期间，隧道进口暴露在空气之中，进口处围岩的冻融状态受空气温度的直接影响[20]。图9为隧道运营20年后，衬砌支护背面最低温度的分布。可以看出：隧道围岩温度沿隧道轴线呈对称分布，最低温度的最小值出现在隧道墙顶DL和DR处，最低温度的最大值出现在仰拱下部G处。因此，将隧道的墙顶处DL和DR处作为隧道发生冻结的最不利位置。图10为隧道运营20年内最不利位置处温度随时间变化。由图可以看出，在隧道运营期，围岩发生冻结的最不利位置处温度随时间呈周期性波动，并且最不利位置处的年最低温度随时间不断降低，在隧道运营后第8年2月2日温度降低至最低，并在随后的年份内年最低温度无明显变化。因此，将隧道运营后第8年2月2日作为隧道内最不利位置发生冻结的最不利时间。

图11和图12分别给出了最不利冻结时间时，无保温层隧道围岩温度和水分分布。由图可以看出，在最不利冻结时间，围岩0 ℃等温线呈环向分布，并且在隧道围岩处径向形成厚度约为2.845 m的冻结圈。围岩水分发生了明显地重分布。沿着冻结圈，围岩的未冻水含量和含冰量变化剧烈，在冻结圈内，靠近隧道衬砌支护的位置，围岩含冰量急剧增大，并达到30%，远远超过了围岩的初始含水量18%，这就是隧道发生冻胀破坏的原因。而在靠近0 ℃等温线的位置处，围岩未冻水含量为18%，含冰量为12%，围岩的总含水量为30%，也超过了围岩的初始含水量18%，这主要是由于在冻融循环作用下，围岩内的水分向冻结锋面发生了迁移。因此，对于严寒地区隧道需施做相应的保温措施，使隧道衬砌不因围岩发生冻结而破坏。

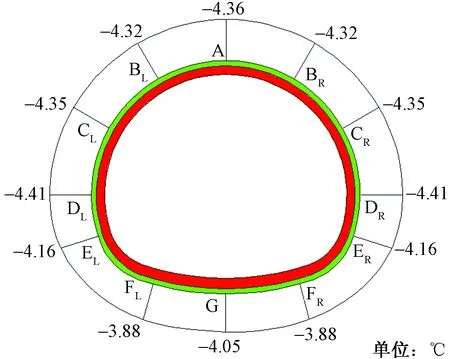
图9 隧道运营第20年初期支护背面最低温度分布Fig.9 The minimum temperature at the boundary of preliminary lining of the selected section in the 20th year

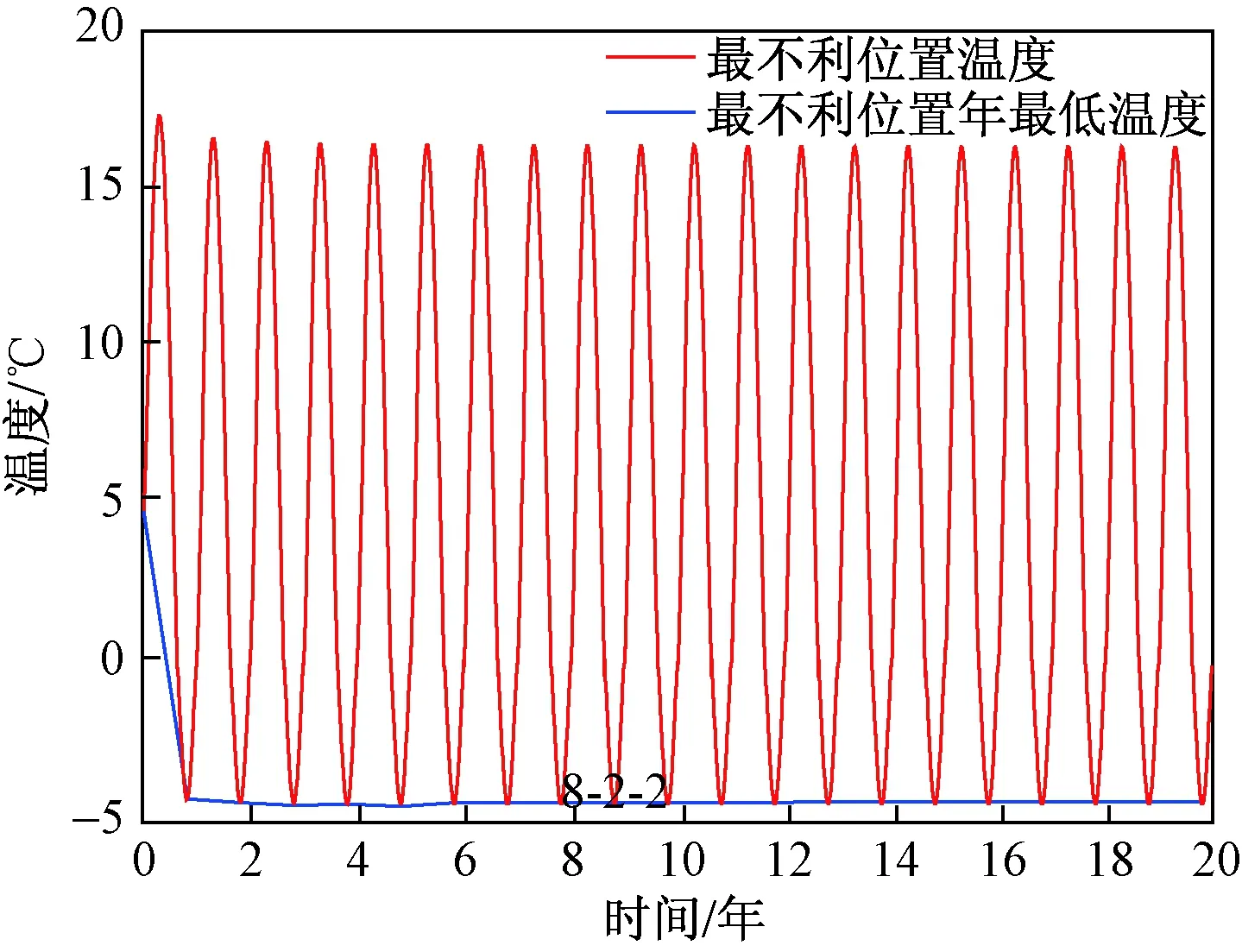
图10 隧道运营20年内最不利位置温度随时间变化Fig.10 Temperature variation at the unfavorable position of tunnel during 20 years

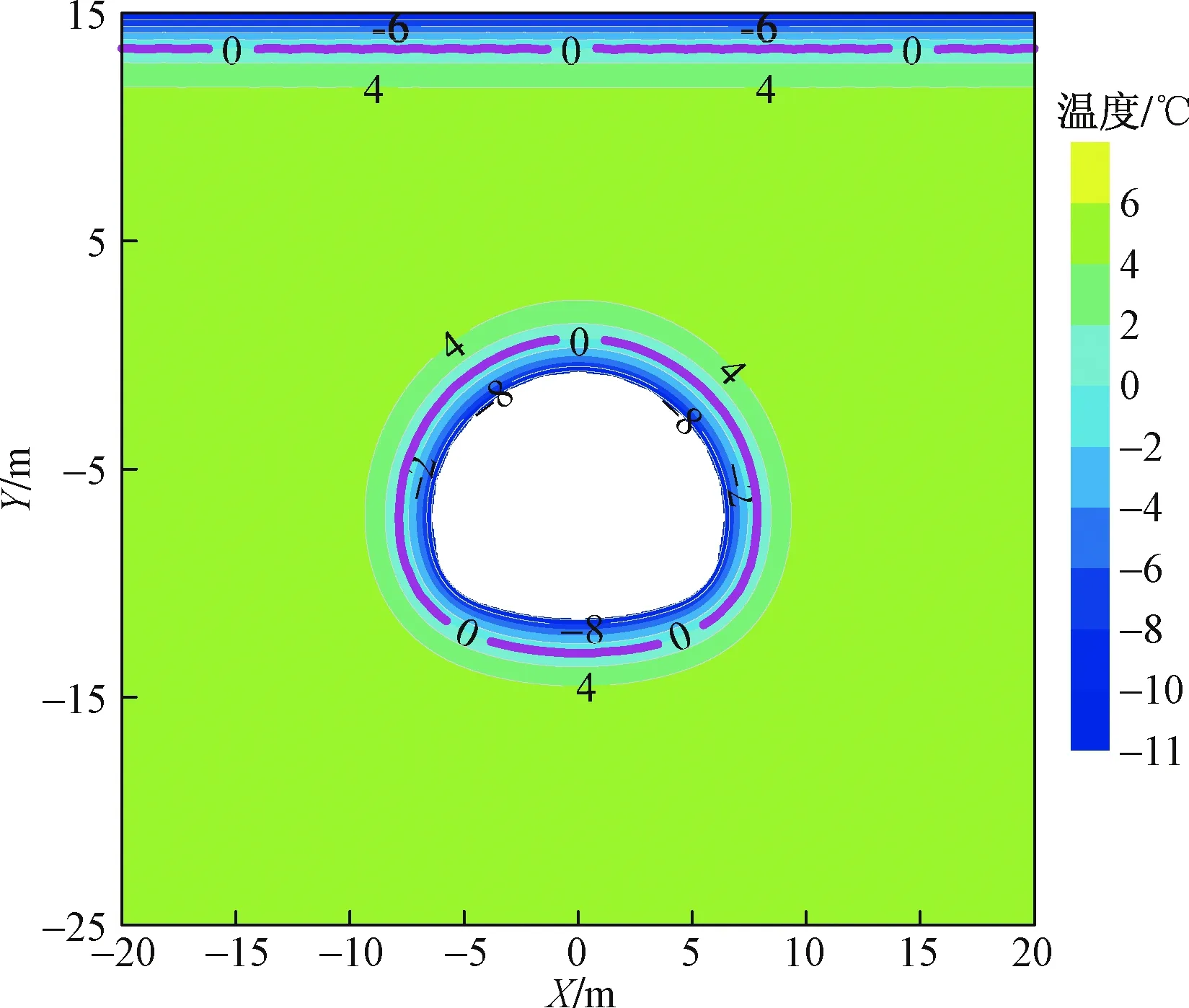
图11 最不利时间时无保温层隧道围岩温度分布Fig.11 Temperature distribution of the selected section of tunnel without thermal insulation layer at the unfavorable time

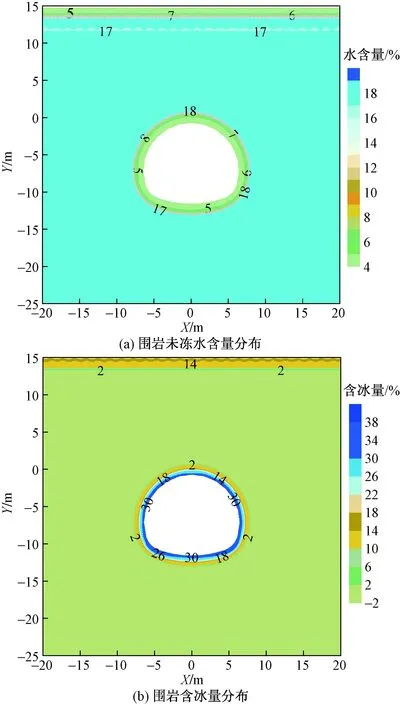
图12 最不利时间时无保温隧道围岩水分分布Fig.12 Moisture distribution of the selected section of tunnel without thermal insulation layer at the unfavorable time

3.2 大气温度对冻结圈的影响

大气温度处于负温是隧道围岩内水分发生冻结的原因，进而引发隧道衬砌的冻胀破坏。所以，对不同温度条件下，冻融圈变化规律的研究必不可少，而温度的变化主要体现在空气年平均温度的变化方面。图13是空气年平均温度分别为1.82、2.32、3.32、4.32、5.32 ℃时隧道的温度分布。可以看出，空气温度对隧道温度场的分布影响巨大，随着空气年平均温度的增大，隧道各位置处的冻结深度显著降低，以隧道墙顶为例，空气年平均温度为1.82 ℃时，墙顶处的最大冻结深度为4.13 m；随着空气年平均温度升高至2.32 ℃，墙顶处的最大冻结深度减小为3.575 m；当空气年平均温度升高至5.32 ℃，墙顶处的最大冻结深度减小为2.048 m。隧道最大冻结深度随空气年平均温度的变化如图14所示，对隧道最大冻结深度随年平均温度的变化拟合函数关系，得

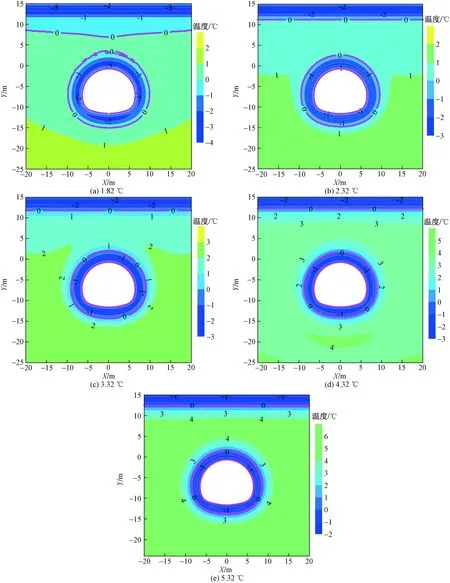
图13 不同空气温度条件下无保温层隧道温度分布Fig.13 Temperature distribution of the selected section of tunnel without thermal insulation layer under different atmospheric temperature

d=6.132 4Ta-0.651 4

(14)

式(14)中：d为隧道最大冻结深度，m；Ta为空气年平均温度，℃。

隧道内不同位置处的空气温度往往与隧道外空气温度不同，如果按隧道外空气温度确定隧道内不同深度处的最大冻结深度会存在误差。运用拟合得到的隧道最大冻结深度与空气年平均温度的变化关系[式(14)]，只需知道隧道内不同深度处的年平均温度，即可确定隧道内不同深度处的最大冻结深度，可以很好地可以解决上述存在的问题，为隧道内不同深度处最大冻结深度的确定提供依据。

图14 隧道最大冻结深度随空气年平均温度的变化Fig.14 Variation in the maximum frozen depth of tunnel under different atmospheric temperature

3.3 保温材料对冻融圈的影响

在寒区隧道工程中，为了防止隧道发生冻胀破坏，常采用围岩注浆，铺设防水层，设置止水带，设置保温层等综合措施，而作为严寒地区隧道防治冻害的有效措施，保温层常常铺设于初期支护与二次衬砌之间以达到防止围岩发生冻胀的目的。现采用上述水-热耦合模型，对铺设导热系数为0.025 W/(m·℃)，厚度为5 cm保温材料的隧道运营8年后的温度场进行分析。

图15为最不利冻结时间时有保温层隧道围岩温度分布。由图可以看出，铺设保温层后，在最不利冻结时间，围岩已无0 ℃等温线存在，这说明保温层的铺设使严寒地区隧道围岩冻结状况得到了明显地改善，降低了围岩水分冻结的可能性，避免了衬砌冻害的产生。

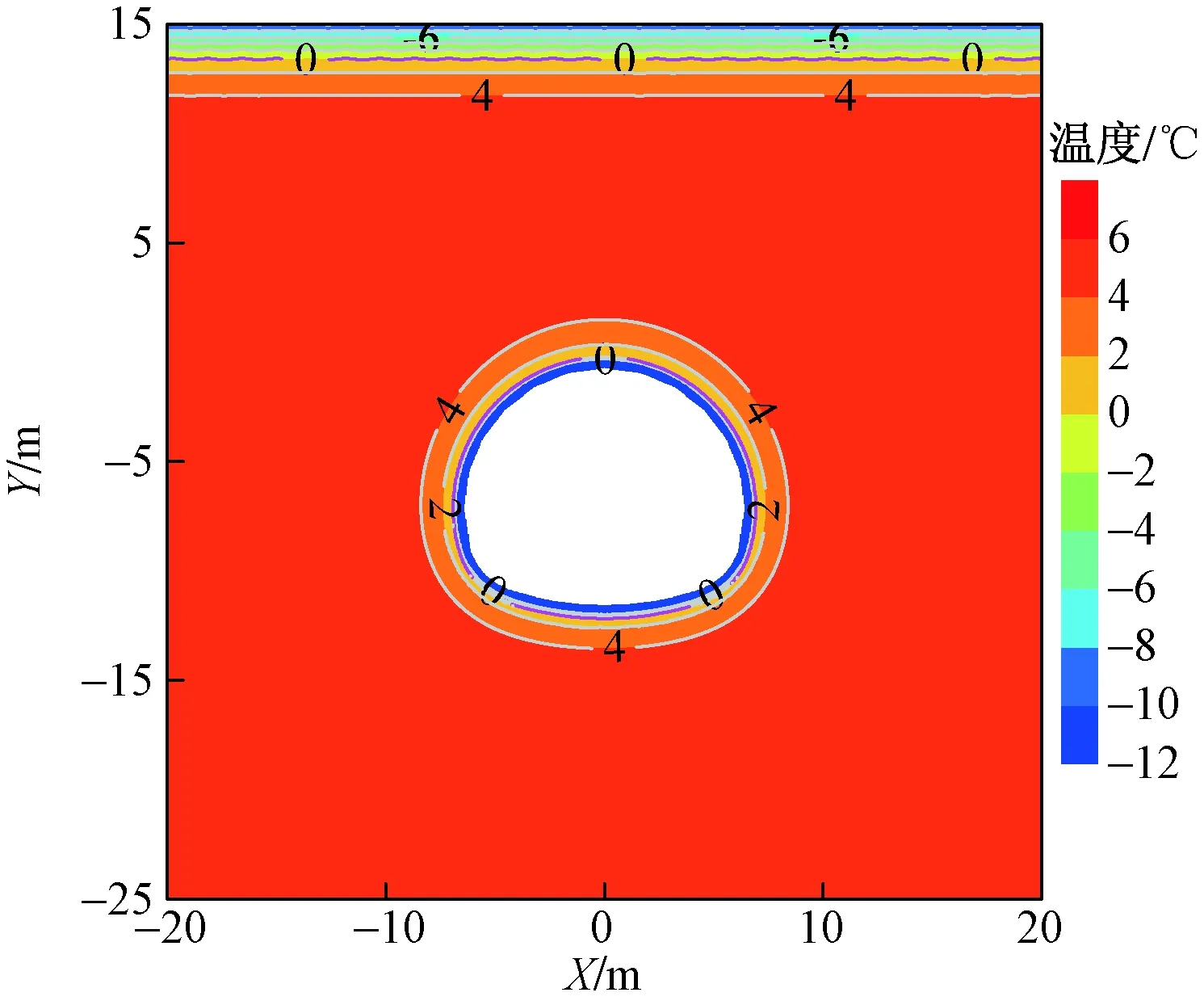
图15 最不利时间时有保温层隧道围岩温度分布Fig.15 Temperature distribution of the selected section of tunnel with thermal insulation layer at the unfavorable time

以隧道墙顶位置处，取二次衬砌表面、初期支护表面和围岩表面作为关键点，分析保温层对隧道保温效果的影响。图16为隧道运营第8年，有、无保温层隧道各关键点温度随时间的变化规律。由图可以看出：隧道衬砌在无保温层时，衬砌表面温度受隧道内空气温度的直接影响，呈正、负温度交替变化，在冷季形成的低温冻结圈在暖季全部融化，如此寒暖交替，冻融反复。而铺设保温层后，虽隧道二次衬砌温度还随时间呈正、负温度交替变化，但初期支护和围岩表面温度全年都为正温，从而避免了围岩水分的冻结。可见，保温层的铺设对严寒地区隧道防冻有重要的意义。

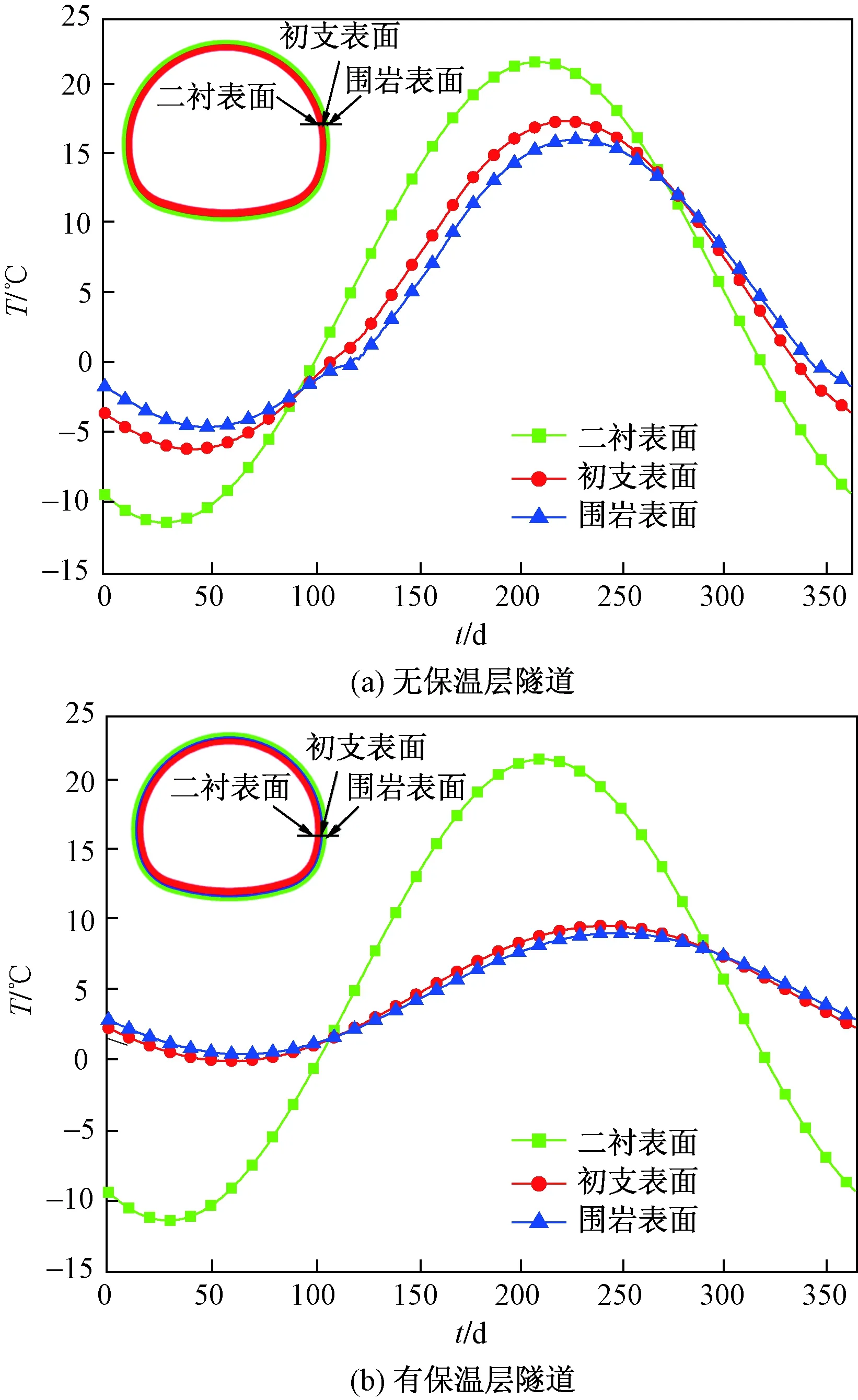
图16 运营第8年无保温层和有保温层隧道关键点温度变化Fig.16 Temperature variation at the classical position of tunnel without and with thermal insulation layer in the 8th year

影响保温效果的一个重要因素是保温材料的导热系数。考虑到目前寒区隧道采用的保温材料的导热系数一般在0.03 W/(m·℃)以下[21]，下面选取五个典型的导热系数λ作趋势分析。图17是隧道分别铺设导热系数为0.008、0.010、0.012、0.015、0.017 W/(m·℃)的保温材料(铺设厚度均为10 cm)时，隧道运行第7～10年时间内，初期支护与保温层接触位置温度变化规律。可以看出，该位置温度变化幅度随保温材料导热系数λ的增加而增加，在隧道表面敷设厚度为10 cm，导热系数为0.012 W/(m·℃)的保温材料后，已经可以保证隧道不出现负温的不利工况。

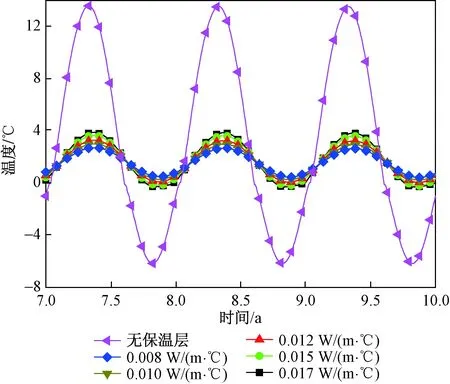
图17 不同导热系数条件下初期支护表面温度变化规律Fig.17 Variation of temperature at the unfavorable position of preliminary lining in the condition of different thermal conductivity

表5为表面铺设不同导热系数的保温材料，隧道运行第7～10年时间内各典型位置的最大冻深。由表可以看出，隧道墙顶的冻深均随着保温材料导热系数的减小而减小，当采用厚度为10 cm，导热系数为0.017 W/(m·℃)的保温材料时，隧道墙顶最大冻深为53.45 cm；当采用导热系数为0.015 W/(m·℃)的保温材料后，墙顶处的冻深减小到了31.04 cm；减小了42%，而当采用导热系数为0.012 W/(m·℃)的保温材料时，墙顶已经不会出现负温的情况，说明隧道防冻与保温层导热系数密切相关。

保温材料对隧道的保温效果不仅受到保温材料类型的影响，还和保温材料的厚度密切相关。图18是隧道铺设导热系数为0.015 W/(m·℃)，厚度分别为8、10、13、14、15 cm的保温材料时，隧道运行第7～10年时间内，初期支护与保温层接触位置温度变化规律。可以看出，该位置处温度变化振幅随保温层厚度的增加而减小，在隧道表面敷设导热系数为0.015 W/(m·℃)厚度为13 cm的保温材料已经能保证隧道不出现负温的不利工况。

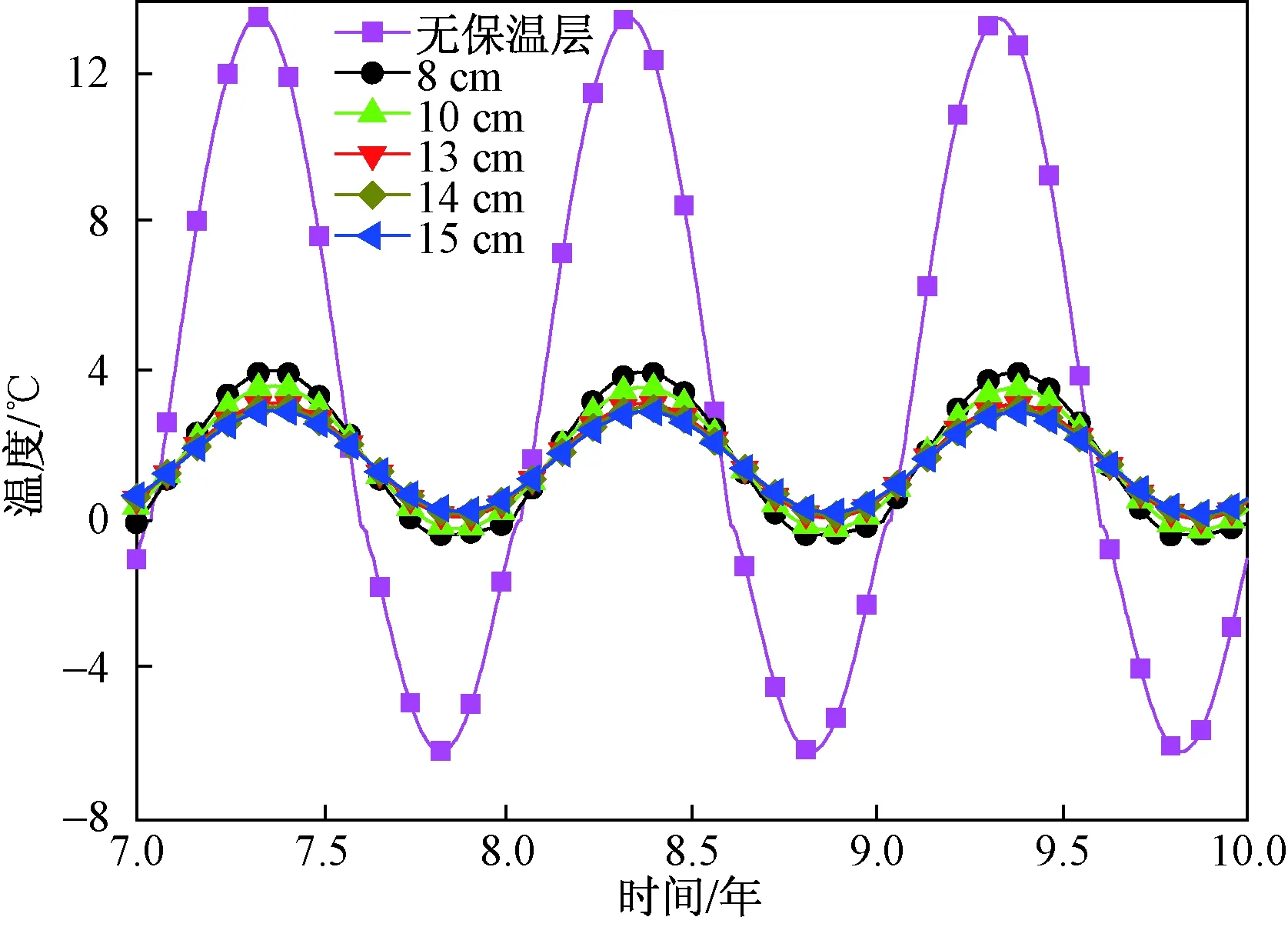
图18 不同厚度条件下初期支护表面温度变化规律Fig.18 Variation of temperature at the unfavorable position of preliminary lining in the condition of different thickness

表6为表面铺设不同厚度的保温材料，隧道运行第7～10年时间内各典型位置的最大冻深。由表可以看出，隧道墙顶的冻深随着保温材料厚度的增大而减小，当保温层厚度为8 cm时，隧道墙顶最大冻深为46.7 cm；当保温层厚度为10 cm时，冻深则减小到了31 cm，减小了33.6%；而当保温层厚度为13 cm时，该位置则已经不会出现负温的情况，说明隧道防冻与保温层厚度密切相关。

表6 最大冻深与保温层厚度的关系

4 结论

(1)本文建立的土体冻结过程中的水-热耦合模型，考虑了水分迁移和冰-水相变潜热对土体冻结的影响，并借助前人的实验结果，通过数值计算的方法验证耦合模型的准确性，计算结果与前人实验结果十分吻合，验证了本文建立的水-热耦合模型在研究土体冻结过程中的有效性。

(2)隧道的墙顶处是隧道发生冻结的最不利位置，最不利位置处温度随时间呈周期性波动，并且最不利位置处的年最低温度随时间不断降低，在隧道运营后第8年2月2日温度降低至最低，以此作为隧道内最不利位置发生冻结的最不利时间。

(3)大气温度是隧道温度场的分布决定因素，随着大气年平均温度的增大，隧道各位置处的冻结深度显著降低，隧道最大冻结深度与年平均温度之间存在一定的关系。因此，可根据隧道内不同深度处的年平均温度确定隧道内不同深度处的最大冻结深度。

(4)保温层的铺设使严寒地区隧道围岩冻结状况得到了明显地改善，避免了衬砌冻害的产生。隧道的冻深随保温材料导热系数的减小而减小，随保温层厚度的增加而减小。对于榆树川隧道，敷设厚度为10 cm，导热系数为0.012 W/(m·℃)的保温材料，则墙顶已经不会出现0 ℃以下的情况；敷设导热系数为0.015 W/(m·℃)，厚度为13 cm的保温材料己经能保证该位置不出现负温的情况。