萌生信息结构 探究证明思路——基于“格式塔”心理学的平面几何教学

□张 昆

（淮北师范大学数学科学学院，安徽淮北 235000）

在探究平面几何证明思路时，题设条件、题断结论与证明思路（简称为“三要素”）都与其所设定的背景情境结构密切相关.因此，只有将证明思路作为整体背景结构的一部分时，探究活动才能起作用.这是“格式塔”（用信息组建轮廓的“完形”，信息轮廓经由准确性检验，形成结构，这种结构是某个平面几何知识或原理的体现）心理学观点所坚持的[1].只有充分考虑“三要素”的背景结构，才有利于探究证明思路.

一、探究平面几何证明思路的途径分析

在探究平面几何问题证明思路时，解题主体应该仔细辨别“三要素”可能设定的情境所隐含的信息轮廓（往往不止一个）特点，并分析这些特点，比照具体公理、定理、性质等平面几何知识结构特点，或在过去的探究证明思路实践中已经萌生并且保存在记忆中的观念，从而赋予信息轮廓以平面几何具体知识结构的意义.可行的命题证明思路，往往蕴含于这种信息特点所生成的背景结构赋予信息轮廓以几何意义中.

发现具有一定难度问题的证明思路，一定不是以题设条件的简单叠加自然推导出题断结论，而是必须利用“三要素”形成（不止一种）轮廓（转化为结构）背景，从中离析出具体的证明思路.思维中的哪些信息要素占据主导地位，这是随着问题的不同特点而不同的，不可能给出一个具体程式.

从信息到组构轮廓，再到检验轮廓形成真确结构的过程，蕴含着平面几何问题证明思路的观念，给平面几何推理论证教学提供了方向、途径与策略.只有通过将“三要素”组成真确结构，才能从中体会与发现证明思路.数学教师离开这条途径的教学方式，必定损伤教学有效性.因此，这种发现对于命题证明教学具有重要现实意义.

二、探究平面几何证明思路的教学示例

陆游诗云：“纸上得来终觉浅，绝知此事要躬行.”《增广贤文》曰：“理在用中方识妙，事非经过不知难.”虽有至善的教学理论，如果不将其与具体的教学实践结合起来，那么教学理论的力量是苍白的，教学实践无法被理论引入到那种至善方向，必定损伤教学有效性[2].以下举例说明运用“三要素”萌生真确结构，探究平面几何问题证明思路的策略与途径.

例 1如图1，在矩形ABCD中，点F是AB的中点，连结CF，过点D作CF的垂线交CF于点E，设AD=a，AB=b.求证

采用分析法，结论①的突出特点就是数据形式，首先考察被开方数，可得：

由形式的相似性，分子可以写成：

由②的诱发，考虑构造容纳②的某个结构形式，联想到勾股定理，于是希冀构造一个直角三角形，并且意识到其两直角边分别为2a与b，与等式③形成关联.由思维的监控系统可以意识到，这条证明思路已经出现.

在图 1 中，由这两组数（式）决定某些要素已经存在，另一些要素还没有出现，可以通过辅助线构造出来，其要素组成的整体结构是直角三角形.如此，延长CF交DA的延长线于G，所要的Rt△CDG就构成了.

图1

证明：延长CF交DA的延长线于G，可得由“边角边”公理知△AFG△BFC，所以，AG=BC=a. 在 △CDG中 ，由 于DC⊥DG，所以

由于DE⊥CG，所以

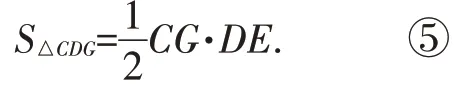
由④⑤知

又CG=（2a）2+b2=4a2+b2，DG=2a，DC=b，将这三个数据代入式⑥，可以解得，DE

这道题所设定的条件与结论，涉及线段长度的数量a，b和的具体特点.因此，在探究证明思路时，考虑结论式①代表的图形特点，让我们联想到直角三角形勾股定理，正是勾股定理结构将相关题设、结论及其蕴含的思路等要素形成几何意义，启发制作辅助线.教学中的关键环节在于，教师应该启发学生从“三要素”中，萌生直角三角形的勾股定理结构，而不应该直接让学生制作这两条辅助线，从而将证明思路给予学生.

例2如图2，平行四边形ABCD中，BF=DG，BF与DG相交于点E，连结AE.求证：AE是∠BED的平分线.

采用分析法，要证明AE是∠BED的平分线，由“角平分线的互逆定理”知，只要过点A作AN⊥BF于N，AM⊥DG于M，并证明AN=AM（记作②），就达到目的.如何证明等式②成立呢？

在解题教学中，由“三要素”组建结构探究证明思路的原理，想到必须要将①②放入一个结构中去，才有可能获得这个问题的证明思路.笔者在长期数学教学实践中，发现了具有不同思维方式的两类情况：

第一种情况，存在少数对图形中线段关系特点特别敏感的学生.这类学生由AN⊥BF与AM⊥DG这两组线段垂直作为背景性条件特点，立即意识到一种运算结构，即试探由①②组成的一种运算关系BF·AN=DG·AM（记作③；题设条件、题断结论与证明思路这“三要素”组成一个结构，结构中应该含蕴证明思路），证明③成立就行了.由③左右两边的积的结构形式，考虑到可证明△ABF与△ADG的面积相等，因为这两个三角形面积都等于平行四边形面积的一半.这类学生的思维具有直觉上突发性领悟的特点，这需要对图形信息（线段垂直）要素关系特别敏感，是偏于几何型思维的一种体现.

图2

大部分学生都很难采用上述这类学生的途径发现证明思路.因此，教师必须要为这类学生开拓更为广阔的背景，这种背景需要探究平面几何证明的经验与观念的指导.这就是第二种情况.通过一段较长时间学习，学生积累了探究平面几何证明思路的经验，应该能够形成这样的观念：其一，绝大多数情况下，教科书（或数学试卷等）所提供的几何证明题不会出现多余的条件；其二，题设条件肯定成立，要证明的结论肯定也成立.第二点可以萌生出探究证明思路的观念，就是如何配置条件因素与结论因素，从而生成某种意义上的一种大的背景结构，在这种背景结构中，可能蕴含证明思路.

那么，如何将上述第二条探究证明题思路的观念应用于这道题中来呢？由于这道题中最为重要的条件是等式①，要证明的结论是等式②，如此，在探究证明思路时，解题主体就会将自己的注意力集中于如何配置①②这两个等式，使这两者组织成一种更大的背景结构，再给这种背景结构赋予具体的几何意义.那么，如何配置①②这两个等式？

一种想法是，将①②的左右两边进行加减乘除运算，在其结果中寻找有意义的几何结构.可以得到这样的一系列等式：

学生需要结合图2的图形直观，辨别出哪些等式有价值？在图2中，等式④⑤⑦很难得到一种像样的几何意义的解释，只有等式⑥，结合图2中的两个线段的垂直关系，可以赋予其几何意义.联结AF、AG，等式⑥两边的两条线段乘积分别是△ABF与△ADG面积的2 倍，都等于平行四边形ABCD的面积.因此等式⑥成立 . 由于BF=DG，故AN=AM，从而AE是∠BED的平分线[3].

两类学生最终都形成一种结构，即等式⑥，没有这样的结构，证明过程就不能发生.然而，达到这个结构的思维途径不同：第一种情况的特点是学生直观上把握图2 的相关要素结构特点，属于直觉领悟；第二种情况的特点是学生没有直接领悟到等式⑥，此时，就需要利用过去探究证明思路所形成的一系列经验与观念的介入.

三、探究证明思路的形式逻辑与背景结构之间关系

对于逻辑推理内涵，丹齐克说得好：“严密推理及其规律是人类智慧的骨架：每一个具有智力的人在他的日常活动中都有机会应用这些规律.他知道，要想严密推理，首先必须把前提作明确的规定，然后一步一步地应用逻辑的规律，最后达到一个结论，这个结论是他使用的逻辑方法所要达到的唯一结果.”[4（]着重号为原文所加）

遗憾的是，许多教师没有认识到，这种严密逻辑不能提供具体论证思路.卡尔文说：“逻辑是论题的一种属性而非精神过程的属性.逻辑性是由对事物的内在秩序的猜测所组成的——但只是当确实有一种明确无误的内在顺序可作猜测时（数学即佳例）.”[5]这说明逻辑推理只能作为说服他人的精致表达结果，它没有提供这种表达结果的来源.因此，借助于平面几何命题论证的学科素材，培养学生探究、发现证明思路的能力显得特别重要.这些逻辑环节是如何产生的？逻辑环节的序列是如何安置的？绕不过由“三要素”组建结构的辅助.

教师具有一种倾向：向学生提供研究好的逻辑证明环节，却把依据题设条件及题断结论的信息要素组成可能结构的合理性排除在外.如此，将逻辑推理还原为受任意综合的零零散散的规则支配的游戏，从而把逻辑过程看作是先天预成的.虽然这种专门化的严密逻辑推理是值得赞赏的，但是如果这意味着真正描绘的是逻辑推理的结果，而不是通过“三要素”萌生结构生成证明思路，那就把主体思维变成贫乏的东西，剥去了作为结果的严密逻辑在真正的创造性过程中可以起到的重要作用，就与课程目标格格不入.

关于形式逻辑与“三要素”的背景结构之间的关系问题是值得所有数学教师深入思考的.不论数学教师对形式逻辑、背景结构与认识论三者之间所形成的关系具有怎样的理解，不论数学教师是否意识到逻辑通路的出现是不是需要正视“三要素”组成的结构问题，这种结构总是客观地确确实实地存在于那里，并且对真正的、有意义的、创造性的、动态的探究证明思路过程总是起着决定性的作用.这是数学教师必须要认识到的.

平面几何证明过程不是简单地在条件叠加过程中得出结论的.对学习主体而言，有些比较困难的问题的证明，一定要通过题设条件、题断结论与证明思路“三要素”的整合，形成有价值的结构（由于整合“三要素”所生成的轮廓不止一个，这种结构的产生有一个价值判断与选择的过程）.数学教师在平面几何推理论证教学中，要特别注意这种形成结构的过程，本文所举的两个例子就很好地说明了这个问题.