单轴晶体表面的反射和透射规律研究

黎昌金, 陈小云, 王登辉

(内江师范学院 a.评估处 b.物理与电子信息工程学院， 四川 内江 641100)

0 引言

近年来，关于电磁波在单轴晶体中的传输特性的研究越来越广泛[1-5]，同时，电磁波从各向同性介质入射到单轴晶体界面时反射与透射规律的研究备受关注.一些学者对双折射中非常光的传播方向进行了讨论[6-8]，非常光的性质也使得菲涅尔公式和反射率与透射率的计算变得复杂，国内外研究人员研究了光轴任意取向等情况下的反射系数和透射系数[9-11]、反射率和透射率[12-14]的表达式，但这些研究主要是在近轴条件下进行的且没有给出反射光和透射光严格具体解析表达式.本文基于麦克斯韦方程组给出了没有近似条件下反射光和透射光的解析表达式，进一步研究反射和透射规律，并对反射率和透射率进行数值仿真，并加以分析和讨论，得到了一些有用结论.

1 单轴晶体中的本征平面电磁波解

取介质表面法向沿z轴，选取入射面为xz平面，则波矢量k将只有xz分量.设介质中平面电磁波解为：

[E,σ0H]=
[ex,ey,ez,-hx,hy,hz]exp[ik0(α0x+γz)-iωt]，

(1)

式中：ex,ey,ez,hx,hy,hz是晶体的本征电磁波分量，下标x,y,z表示方向.σ0是波阻抗，引入它是为了使ey,hy具有相同的量纲，从而简化以后的表述.hx前的“-”号可以使后面的本征值方程具有一定的对称性.k0α0,k0γ分别为波矢量在x,z方向上的分量,ω为固定电磁波的圆频率.σ0,ω和α0是已知量，根据边界条件，可由入射电磁波得到.ex,ey,ez,hx,hy,hz为晶体的本征电磁波分量大小，γ,ex,ey,ez,hx,hy,hz是待求未知量.

在光学范畴中，晶体是非铁磁性物质，对磁场不呈现各向异性.所以单轴晶体的磁导率张量在主轴坐标系下和非主轴坐标系下的张量矩阵相等且为单位对角矩阵.单轴晶体中的平面电磁波解满足的麦克斯韦方程组和媒质的本构关系，在光波传播的空间即远离辐射源的区域，不存在自由电荷与传导电流(J=0)，于是把式(1)代入麦克斯韦方程组化简得到γ,ex,ey,ez,hx,hy,hz满足的方程为

(2)

式中：ε11,ε12,ε13,ε22,ε23,ε33为单轴晶体在非主轴坐标系下介电常数的各个分量大小，满足

(3)

(4)

消去式(2)中ez,hz后，整理得到ex,ey,hy,hx满足的本征值方程为：

(5)

它是一个4×4的矩阵本征值方程.在一般情况下，式(5)的本征值难以用解析式来表达，但易于采用成熟的本征值数值计算程序获得.在不是全反射的情况下，其本征值必为两正两负的实数，因为它在物理上对应于两个顺着z轴的上行波和两个逆着z轴的下行波.设求得的本征值γ和本征矢量W分别为

(6)

(7)

式中：γj对应于本征矢量矩阵W中第j列的本征矢量，其分别表征电磁场的对应方向上的传输波矢；W表征透射波的本征横向电磁波解.4个本征值对应着四个独立的模式场，且在反射和透射空间中，电磁场都可以表示为四种基本模式场的叠加形式.因此电磁场的横向分量表示成

(8)

式中：u1,u2分别表示基本模式场上行波的振幅系数；d1,d2分别表示基本模式场下行波的振幅系数.当界面两侧的介质确定后，振幅系数和本征电磁波分量也确定，两者结合即为具体的横向电磁波分量.将式(7)代入式(2)可得四个独立的模式场的本征纵向分量解.在各向异性介质中各有两个上行波和下行波，所以通常把它分为Ι型波和ΙΙ型波，但是在各向同性介质中各自两种电磁波退化为一种.在单轴晶体中本征值为正对应的两个模式场分别为o光和e光，在这里定义γ1和γ2对应的电磁波分别为o光和e光，γ1和γ2对应的电磁波分别为垂直自己主平面和在自己主平面内的Ι型波和ΙΙ型波.

2 各向同性晶体入射到单轴晶体表面的反射和透射行为

设入射波一侧是各向同性晶体，入射电场强度方向与入射面的夹角为ψ，入射角为θ，如图1所示.

图1 向同性晶体入射到单轴晶体表面的光路示意图

设单位入射线偏振波的电场强度可表示成

(9)

(10)

式中：ε是各向同性晶体的介电常数.通过求解本征值方程得到各向同性晶体满足的本征值和本征矢量的解析表达式分别为

(11)

(12)

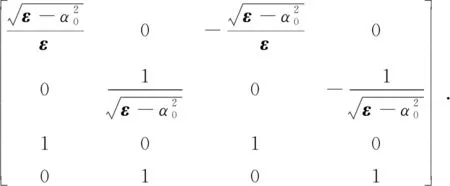
(13)

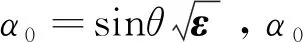
(14)

为了便于计算和物理分析，定义反射系数阵R和透射系数阵T：

(15)

式中：R代表入射一侧电磁波的反射系数阵;Rps代表入射的s波反射到反射的p波的系数，类比可得到其他反射系数的物理意义;T代表入射一侧的电磁波透射到另一侧的电磁波的透射系数阵;T1p代表入射的p型波透射到透射的Ι型波的系数，类比可得到其他透射系数的物理意义.

利用式(15)，注意到d1=d2=0，于是式(14)改写成另外形式的横向分量方程组为

(16)

式中，未知量较多且不知是否为0，讨论其解析解相对困难，但当入射介质、透射介质，入射光确定后，易于采用计算机程序计算得到反射系数和透射系数.

根据界面两侧的本征值方程得到入射区域和透射区域的电磁场的横向分量解为：

(17a)

(17b)

(17c)

由式(7)和式(17a)可得

(18)

(19)

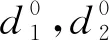
单轴晶体中e光传播方向不一定在入射面内，e光的折射率相对复杂，本文不作讨论.而o光传播方向与波法线方向相同，即光的折射率与各向同性介质中计算无异.设单轴晶体中o光的折射角为θ1，则

(20)

于是单轴晶体中o光的折射率为

(21)

定义反射率和透射率分别为反射能流的分量的时间平均值和透射能流分量的时间平均值与入射能流分量的时间平均值之比，根据电磁波能流密度分量的平均值计算公式，可得

(22)

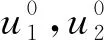
欧拉旋转可以改变单轴晶体取向，根据本文的旋转定义，欧拉角Φ和Θ改变光轴的取向，Ψ改变除光轴的另外两个主轴的取向问题.文献[12]中并没有考虑另外两个主轴绕光轴旋转对反射和透射规律的影响.图2和图3采用与文献[14]相同的参数下，改变Ψ的角度，对比发现绕光轴旋转，对反射率无影响，但对透射率的影响较大;Ψ=0o时即入射波电矢量平行于界面，反射率ηs始终为0;在θ=58.54o有ηp=ηs=ζe=0，此时透射率ζo达到最大值1;在θ∈(58.54°,90°)ηp=ζe=0，此时反射波和透射波能量互补，透射波只有o光.少有学者具体详细讨论入射波电矢量对光波规律的影响，对比图2和图4发现，ψ角的改变即入射波电矢量方向的改变对光波规律影响较大;Ψ=90o时即入射波电矢量平行于界面，反射率ηp始终为0，在θ∈(58.54°,90°)ηp=ζe=0，此时反射波和透射波能量互补，透射波只有e光.对比图2、图4和图5可发现入射波电矢量不平行于界面或者不垂直于界面时，反射波平行分量始终为0.

图2 ψ=0o,Φ=40o,Θ=45o,Ψ=45o时反射率和透射率随入射角变化的曲线图

图3 ψ=0o,Φ=40o,Θ=45o,Ψ=25o时反射率和透射率随入射角变化的曲线图

图4 ψ=90o,Φ=40o,Θ=45o,Ψ=45o时反射率和透射率随入射角变化的曲线图

图5 ψ=35o,Φ=40o,Θ=45o,Ψ=45o时反射率和透射率随入射角变化的曲线图

3 结束语

研究了平面电磁波从各向同性介质入射到单轴晶体表面时，界面两边的光波具体表达式，给出了反射率和透射率的解析表达式.本文选取方解石为对象，数据结果表明反射波和透射波满足能量守恒定律.当晶体绕光轴旋转时，反射率不受影响，而透射率影响较大.当入射波电矢量方向改变时，反射率和透射率都要发生改变.在一定条件下不仅可以实现光波选择，而且可实现偏振分离，偏振度可达到90%.本文的研究理论更加的严格和完善，得到的公式更具普遍性.

本文的研究方法还可用于研究透射波的传播方向，折射率等其他物理性质，但需要考虑欧拉角和入射角的关系.研究方法也同样适用于双轴晶体，但由于计算机求解本征值方程时，本征值矩阵的结果具有随机性，分辨两种透射光对应的本征值相对困难，有待进一步研究.