基于温度与压力双重作用的致密储层渗透率定量评价模型

王居贺， 刘 彪， 杨 虎， 周鹏高

(1.中国石化西北油田分公司石油工程技术研究院， 乌鲁木齐 830011； 2.中国石化缝洞型油藏提高采收率重点实验室， 乌鲁木齐 830011； 3.中国石油大学(北京)克拉玛依校区， 克拉玛依 834000； 4.克拉玛依职业技术学院, 克拉玛依 834000)

渗透率是评价储层物性的重要参数，对油气产量具有决定性影响，研究储层渗透率的变化规律对于油气生产具有重要意义[1-2]。由于储层岩石所受应力变化而引起的渗透率损失称为应力敏感[3-4]，该问题是近年来石油工程领域的研究热点之一。目前渗透率变化规律研究主要依赖于室内实验，对实验结果进行拟合得到渗透率与有效应力的关系式，进而评价油气开采后储层渗透率的变化。

然而，常规应力敏感室内实验存在较大的局限，主要表现为以下3点：

①施加的载荷与储层岩石实际受力状态差异甚大。通常采用固定内压(孔隙压力)，外压(围压)先增大后减小的方式进行测试，实际储层油气采出过程中，内压(孔隙压力)降低，而外压(地应力)不变。另外，由于实验难度及安全风险，施加的内压、外压远小于实际储层的真实受力[5]。

②未考虑温度的影响。目前的实验未考虑到油气采出过程中储层温度降低这一因素。

③未能证实渗透率测试过程中岩心是否发生塑性变形。通过增大围压，再减小围压到初始状态，发现渗透率要远小于初始状态，学者们将该现象解释为“有效应力增大使岩心发生塑性变形，应力释放之后岩心内部孔喉尺寸不能恢复到初始状态”[6-9]。然而，该解释缺少岩心发生塑性变形的直接证据，因此有学者对此提出质疑并引起学术争议[10-14]。

针对目前实验研究存在的问题，在假定岩石仅产生弹性变形的前提下，根据多孔介质弹性力学理论，推导出岩石孔隙体积和尺寸的应力-应变关系，再应用管流模拟渗流，得到渗透率随温度、孔隙压力变化的定量计算模型。现通过改进实验方法，模拟真实储层温压条件，开展岩心力学和渗透率同步实验，实验结果验证理论模型的正确性。

1 储层温度、压力的变化规律

油气未开采前，储层温度、压力为原始地层温度和原始孔隙压力。随着油气采出，近井地带储层温度、压力急剧降低，而远离井眼的区域，储层温度、压力接近原始状态。储层温度、压力变化规律如图1所示。

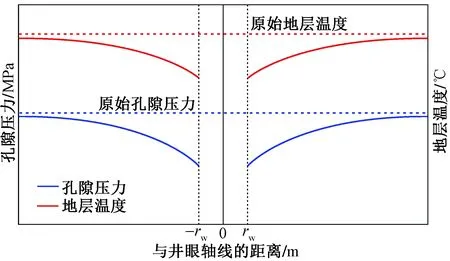
rw为井眼半径图1 油气采出后地层温度、压力变化规律Fig.1 Law of formation temperature and pressure change after oil and gas production

取一岩石单元体为研究对象，初始受力状态如图2(a)所示。油气采出之后，外应力不变，孔隙压力降低Δpp，地层温度降低ΔT，温度变化之后在三个主应力方向分别产生温度应力ΔσT，如图2(b)所示。

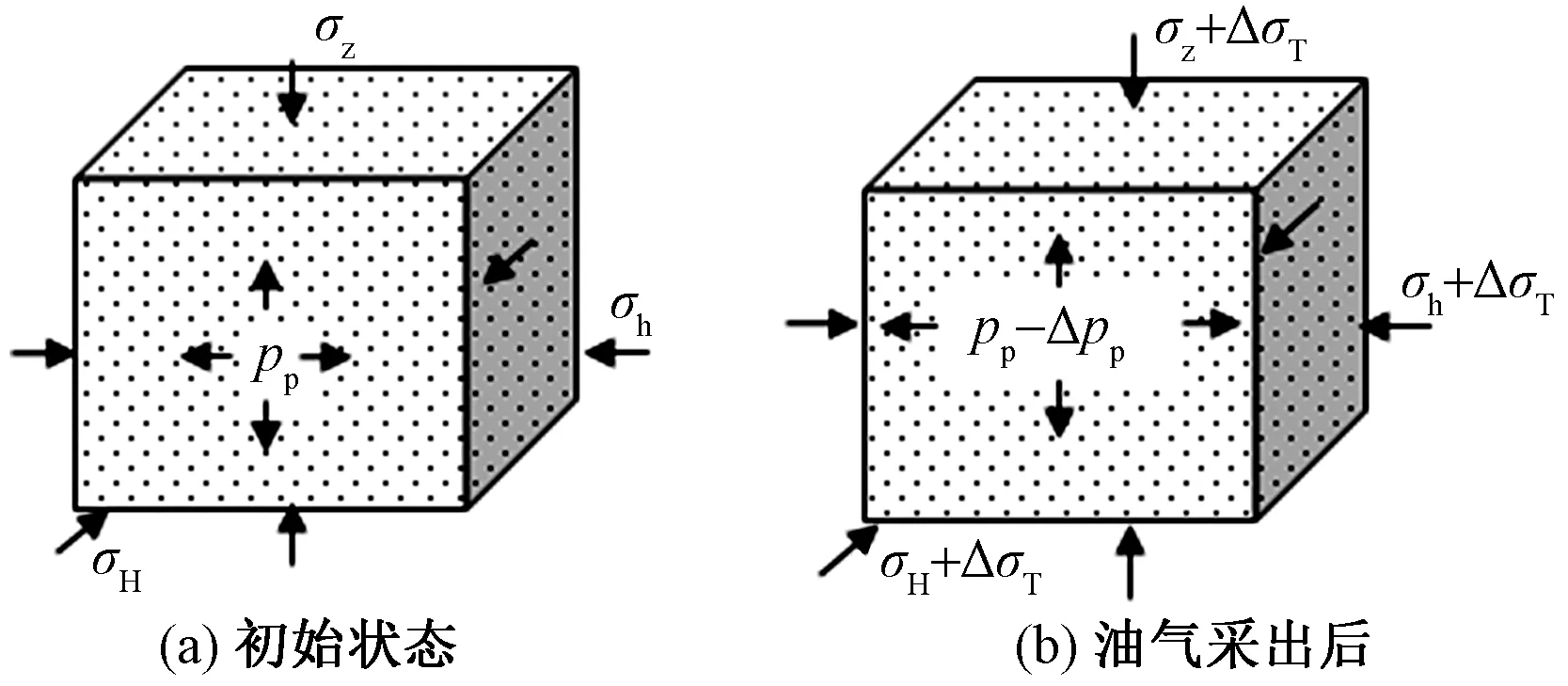
σz为纵向上的垂向应力，又称上覆岩层压力；σH、σh分别为水平方向的最大、最小水平主应力；pp为所受到的内应力(孔隙压力)图2 储层岩石单元体受力状态Fig.2 Reservoir rock unit cell stress state

2 渗透率定量评价模型

假设在储层温度和孔隙压力降低双重作用下，储层岩石只产生弹性变形。首先分析油气采出前、后储层岩石的受力变化，再根据多孔介质弹性力学理论，求解岩石孔隙体积应变；应用管流模拟渗流，得到岩石中毛管尺寸的变化，根据Kozeny-Carman方程即可得到渗透率变化的定量评价模型。

2.1 岩石孔隙体积应变

储层岩石初始状态所受的有效应力[15]为

(1)

式(1)中：σeH、σeh、σez分别为岩石在三个正交方向所受的有效应力，MPa；φ0为初始状态岩石孔隙度，%。

岩石所受的总有效应力为

σe=σeH+σeh+σez=σH+σh+σz-3φ0pp

(2)

在弹性变形范围内，应力变化会使岩石外观体积与孔隙体积同步(等比例)变化，岩石的孔隙体积发生变化，但孔隙度不变[16]，即

φ0=φ1

(3)

式(3)中：φ1为应力改变之后岩石孔隙度，%。

由于外应力(地应力)不变，假设孔隙压力降低Δpp(Δpp>0)，根据式(2)，总有效应力增大3φ0Δpp，岩石孔隙体积应变(孔隙体积减小)为

(4)

式(4)中：E为弹性模量，MPa；ν为泊松比。

若岩石的热膨胀系数为αL(单位为℃-1)，温度降低ΔT(ΔT>0)，则由温度降低导致的孔隙体积应变(孔隙体积增大)为

ε2=-3αLΔT

(5)

由于温度和孔隙压力降低双重作用，导致的岩石孔隙体积总应变为

(6)

2.2 管流模拟渗流

流体在储层岩石中的渗流，可以用一束管子的管流进行模拟[17]。致密储层一般裂缝不发育，属于孔隙型储层，应用管流模拟渗流时假设岩石中不含裂缝。初始状态，假设岩石中有n个长度为Lp的毛管，毛管平均半径为r0，迂曲度为τ0，岩石孔隙度为φ0，渗透率为K0；油气采出之后，毛管长度不变，毛管平均半径为r1，迂曲度为τ1，岩石孔隙度为φ1，渗透率为K1。

初始状态、油气采出之后毛管体积分别为

(7)

(8)

油气采出前、后，毛管体积关系满足

V1=V0(1-ε)

(9)

由式(7)～式(9)可得

(10)

相对于岩石尺寸，岩石的弹性变形量极小，因此油气采出前、后毛管迂曲度几乎不变，可近似认为

τ0=τ1

(11)

渗透率可根据Kozeny-Carman方程[17]计算，即

(12)

(13)

油气采出之后，渗透率损失百分数Sk为

(14)

将式(3)、式(10)、式(11)代入式(14)可得

(15)

式(15)即为温度与压力双重作用下储层渗透率定量评价模型。

从式(4)可以看出，孔隙体积应变与弹性模量、孔隙压力降低值、孔隙度和泊松比有关，由于弹性模量比其他参数大若干个数量级，因此孔隙压力下降引起的孔隙体积压缩量很小。从式(5)可以看出，孔隙体积应变与岩石的热膨胀系数成正比，由于热膨胀系数很小，温度降低导致的孔隙体积增大量也很小。从式(15)可以看出，油气采出过程中，一方面孔隙压力下降，岩石压缩，孔隙体积减小，渗透率趋于减小；另一方面，地层温度下降，岩石骨架冷缩，孔隙体积增大，渗透率趋于增大。两方面对渗透率的影响具有相互抵消的作用。

2.3 计算讨论

根据式(15)，固定其他参数，定量计算了孔隙压力降低、弹性模量、地层温度降低和热膨胀系数对渗透率的影响。各参数取值为：φ0=15%、E=10 000 MPa、ν=0.25、αL=5×10-5℃-1、Δpp=25 MPa、ΔT=25 ℃。计算结果如图3所示。

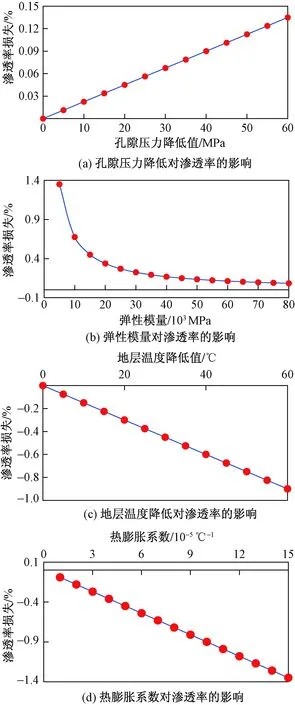
图3 渗透率影响因素分析Fig.3 Analysis of factors affecting permeability

从图3(a)可以看出，随着孔隙压力降低，渗透率损失线性增大，孔隙压力下降60 MPa，渗透率损失0.13%；从图3(b)可以看出，随着弹性模量增大，渗透率损失先急剧减小，后趋于平缓；从图3(c)可以看出，随着地层温度降低，渗透率损失负线性增大(渗透率线性增大)，地层温度降低60 ℃，渗透率增大0.9%；从图3(d)可以看出，随着热膨胀系数增大，渗透率损失负线性增大(渗透率线性增大)。相对于其他因素，弹性模量和热膨胀系数对渗透率的影响更大。总体来看，温度与孔隙压力变化之后，储层岩石渗透率变化较小，一般不超过±2%。

3 实验验证

3.1 实验方法

实验设备采用法国Sanchez Technologies公司生产的高温高压岩石物理力学测试系统，该系统主要由高温高压室、围压、轴压和孔隙压力控制系统、应力-应变测试系统、波速测试系统、声发射测试系统、渗透率测试系统和计算机总控系统等组成(图4)。该系统的围压、轴向压力加载精度为±2 MPa；可施加孔隙压力为0～60 MPa，精度为±1 MPa；测试温度可达200 ℃，精度为±2 ℃；流量精度为±2%。该系统能够满足储层温度和压力条件下渗透率的测试。

图4 高温高压岩石物理力学测试系统Fig.4 High temperature and high pressure rock physical and mechanical testing system

选取吉木萨尔凹陷芦草沟组页岩油、克拉美丽气田石炭系火成岩、塔河油田三叠系中油组致密砂岩3种典型致密岩性储层的全直径岩心[18-20]，再从同一全直径岩心上小范围(深度变化小于30 cm)内钻取标准试样3块，以保证试样性质的同一性；其中2块用于开展全应力-应变力学测试，确定弹性极限；1块用于开展渗透率测试。为确保试样质量，避免试样内部出现微裂隙和缺陷，在加工试样之前对全直径岩心纵向和上、下切面进行CT扫描。共钻取9块标准试样，如图5所示。

图5 三种典型致密储层实验岩心样品Fig.5 Three typical tight reservoir core samples

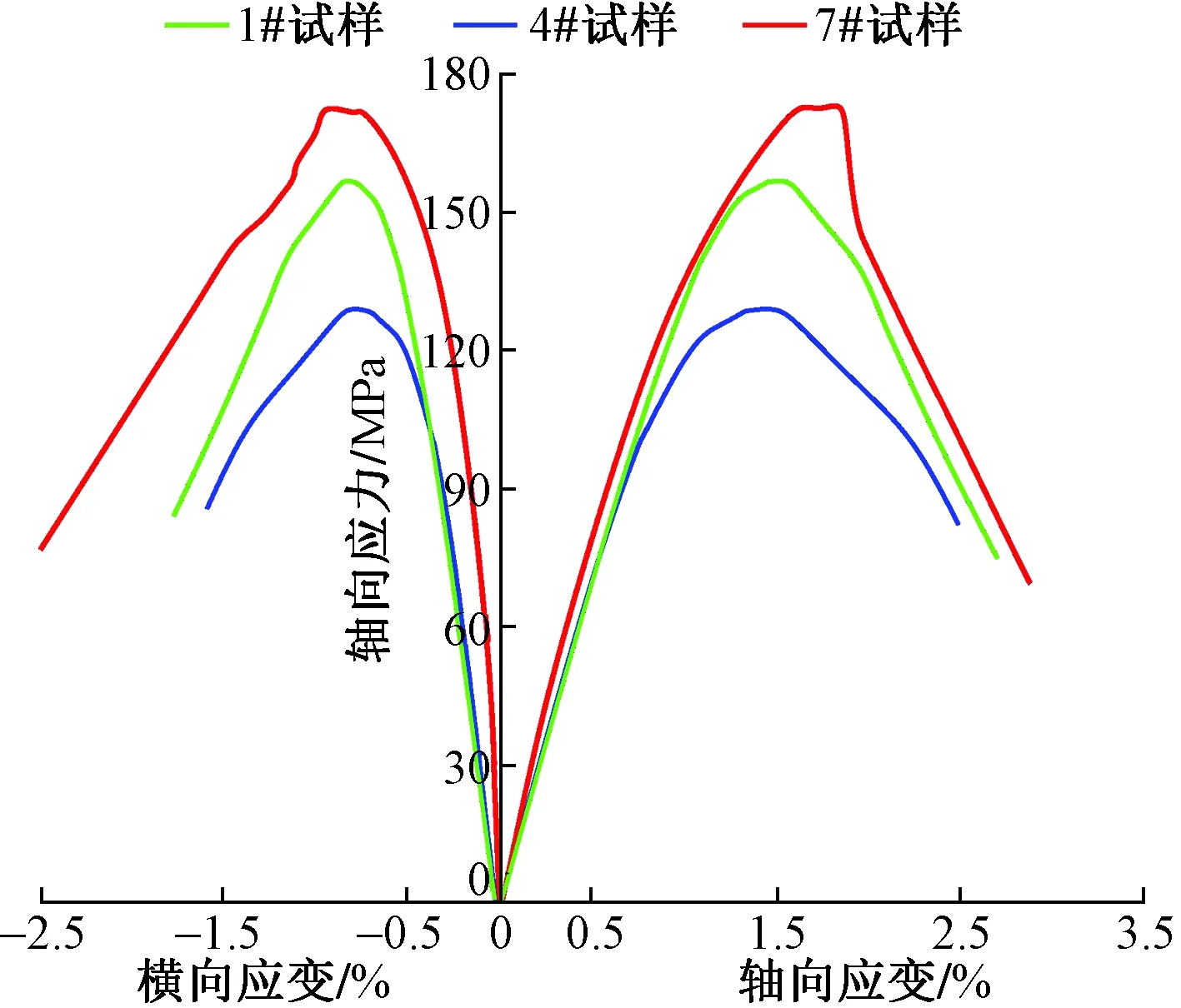
图6 试样应力-应变测试结果Fig.6 Full stress-strain test results of specimens

3.2 岩心力学测试结果

对1#、2#、4#、5#、7#、8#试样进行全应力-应变测试，结果如表1、图6所示。由于试样钻取深度变化范围很小，取自同一全直径岩心的试样力学性质十分接近。

3.3 渗透率实验结果与理论计算对比

采取固定围压和轴压，改变内压(孔隙压力)和温度的方式，对3#、6#、9#试样进行了渗透率测试，结果如表2所示。

表1 岩心试样力学测试结果Table 1 Mechanical test results of specimens

表2 岩心渗透率测试结果Table 2 Core permeability test results

3#、6#、9#试样渗透率测试过程中施加的围压和轴压分别为65、80、90 MPa，与其地下原位状态所受的平均地应力接近；施加的初始内压接近储层原始孔隙压力，初始温度接近储层原始温度。降低内压、温度测得的渗透率与初始状态渗透率进行比较，即为实测渗透率损失。 根据岩心力学测试结果(表1)可知，3#、6#、9#试样施加的围压和轴向压力小于弹性极限，渗透率测试过程中试样只产生弹性变形，因此可利用式(15)计算渗透率损失。从表2可以看出，本文模型计算的渗透率损失与实测透率损失吻合良好。

4 结论

(1)根据多孔介质弹性力学理论，推导出岩石孔隙体积和尺寸的应力-应变关系，再应用管流模拟渗流，得到渗透率随温度、孔隙压力变化的定量计算模型。该模型适用于裂缝不发育的致密岩石在弹性变形范围内的渗透率定量计算。

(2)随着油气采出，孔隙压力下降，岩石所受有效应力增大，孔隙体积压缩，渗透率减小；同时地层温度降低，岩石骨架冷缩，孔隙体积增大，渗透率增大；两方面对渗透率的影响具有相互抵消的作用。

(3)油气开采过程中，渗透率变化与孔隙压力降低值、孔隙度、弹性模量、泊松比、热膨胀系数和温度降低值有关。由于温度、孔隙压力变化引起的储层岩石渗透率变化很小，一般不超过±2%。