无人旋翼机旋翼气动分析与试验研究

吴裕平，解 望

（中国直升机设计研究所，景德镇333001）

自转旋翼机（又称“旋翼机”）是一种以自转旋翼作为升力面、螺旋桨推/拉力作为前进动力的旋翼类飞行器。旋翼机与飞机不同，它主要靠旋翼产生升力，而没有固定机翼或只有辅助机翼。旋翼机与直升机也不同，它的旋翼和发动机没有连接，不能提供前进拉力和操纵力矩。旋翼机结构简单，失速速度小，起飞距离短，安全性高，成本低，所以受到大众喜爱。近年来无人飞行器发展迅速，无人旋翼机也应运而生[1]。

旋翼机的诞生早于直升机，通过不断试验和总结研制的Cierva C.4 型旋翼机在1923 年飞行成功[2]。20 世纪60～70 年代，美国联邦航空管理局（FAA）认证McCulloch J-2 和Umbaugy 旋翼机，两型 机 各 生 产 约100 架[3-4]。21 世 纪，小 型 载 人 旋 翼 机在航空爱好者中得到广泛发展，美国格莱恩兄弟航空公司和Carter 公司使用现代航空技术让旋翼机再次成为热点[5-6]，迄今美国旋翼机拥有量达2 万余架，但这些主要是载人旋翼机，针对无人旋翼机的技术研究和产品研制较少。

旋翼机的旋翼依靠前方来流吹动，始终处于自转状态，飞行中旋翼桨盘向后倾斜，气流从下往上穿过桨盘[7]。直升机的旋翼在发动机驱动下，自上向下吸入空气穿过桨盘。因此，许多国家研究机构纷纷对旋翼机特殊的气动环境开展研究，但无人旋翼机的相关研究并不多见。1994 年，美国开展了直径1.06 m 无人旋翼机2 片桨叶旋翼90°迎角自转风洞试验[8]，2004 年，Maryland 大学针对空中抛放式无人旋翼机，进行了自转旋翼起转特性的试验研究[9-10]，研究方向主要是飞行动力学和飞行控制。国内王焕瑾团队研究了自转旋翼的气动优势，以及保持稳定飞行的旋翼转速关系[7]。朱清华博士对旋翼机关键技术进行了深入研究，并完成了1 650 kg ZX1 型旋翼机总体方案设计[11]。

旋翼机在不同飞行速度下，通过操纵旋翼轴倾斜角度，稳定旋翼转速，并得到所需要的升力，用于平衡全机重力[11]。旋翼一直保持自由旋转，旋翼功率表述为旋翼阻力与飞行速度的乘积，需要发动机传输给螺旋桨的可用功率来解决[12]。

本文针对某无人旋翼机方案设计需求，建立旋翼机气动模型进行无人旋翼机气动力计算，开展设计参数对旋翼气动特性的影响研究，得到了旋翼拉力和轴倾角操纵规律，并完成风洞试验验证。

1 旋翼气动设计参数

旋翼设计参数主要包括桨盘载荷、旋翼半径、桨叶片数、旋翼实度及桨叶弦长等。无人旋翼机属于轻小型，桨盘载荷较小，一般小于12 kg/m2[13]。在起飞总重量G 和桨盘载荷p 确定的情况下，可以根据下式确定旋翼半径R

无人旋翼机采用两片桨叶和跷跷板式桨毂，旋翼实度较小。确定了旋翼实度σ 和桨叶片数k，就可以确定桨叶弦长b

本文研究的无人旋翼机起飞质量为22 kg 左右，旋翼实度为0.045，采用OA212 翼型的矩形布局。旋翼桨叶采用无扭转设计，即气动扭转角沿桨叶展向不变化。

2 旋翼气动特性分析

2.1 旋翼气动模型

从叶素理论出发，引入动态入流求解诱导速度的非均匀分布，表达式为

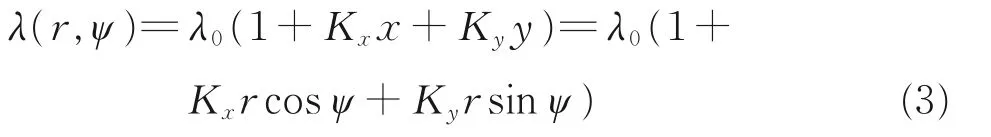
式中：r 为桨叶径向位置，ψ 为方位角，λ0为诱导速度平均值，Kx、Ky为前飞状态诱导速度变化参数。

然后，根据诱导速度计算桨叶各处剖面的相对来流速度和来流角。剖面合速度为

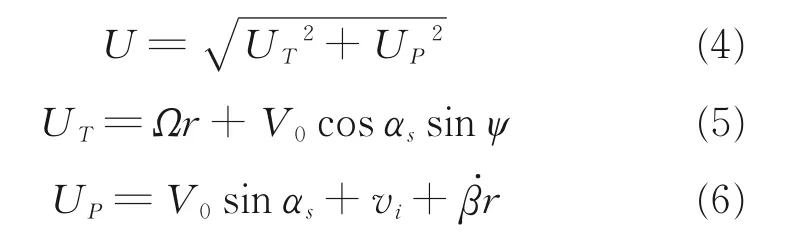
桨叶剖面迎角包括剖面安装角θ（无总距操纵）和来流角α，关系式为

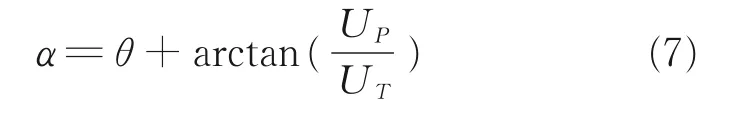
式中：UP为剖面垂向速度，UT为切向速度，Ωr为旋转线速度，V0为飞行速度，αs为旋翼轴倾角，vi为各处诱导速度（与λ 对应），β̇为挥舞角速率。根据马赫数和迎角，可得叶素升力和阻力为

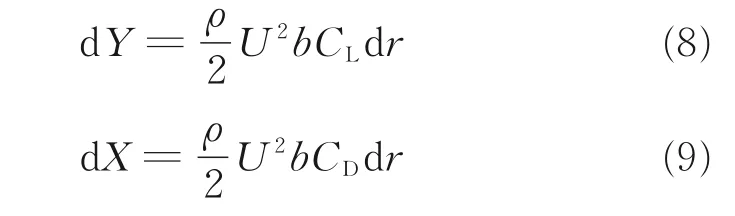
式中:ρ 为空气密度，CL、CD为剖面翼型的升力系数和阻力系数，dr 为桨叶微段长度。再转化为叶素拉力（平行旋翼轴方向）和旋转阻力

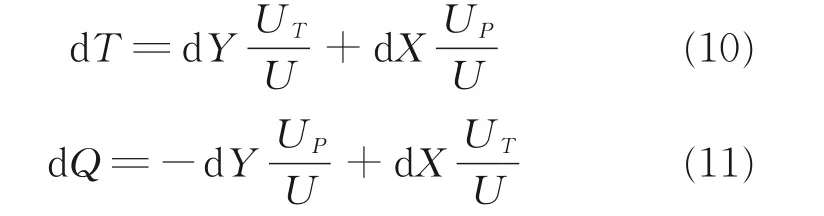
最后，积分各个叶素拉力和阻力，就得到整片桨叶的气动力，再考虑各方位角下K 片桨叶相加得到整个旋翼气动力。

2.2 旋翼半径影响

作为旋翼机的升力面，旋翼升力与旋翼半径、总距紧密相关，首先分析半径对旋翼性能的影响。

在总距为1°、桨尖速度为120 m/s 的情况下，旋翼半径从1.2 m 增加到1.8 m，旋翼轴倾角基本不变，旋翼拉力明显增大，从180 N 增加到400 N左右。如图1 所示，旋翼轴倾角随着飞行速度增大而减少，当飞行速度为16.67 m/s 时，旋翼轴倾角约为13.95°，而当飞行速度增加到33.33 m/s 时，旋翼轴倾角迅速降低至4.18°。如图2 所示，其他参数不变时，随着旋翼半径加大，旋翼升力相应增大。旋翼拉力随着飞行速度增加而略有降低，由于此时旋翼轴倾角（竖直为0°，后倒为正）也降低，因此旋翼升力能够维持不变，从而平衡全机重力。

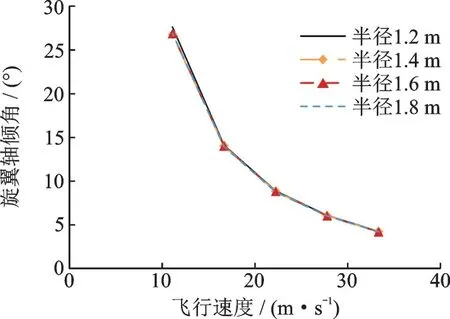
图1 不同半径下旋翼轴倾角随飞行速度变化曲线Fig.1 Rotor shaft angle varying with fight speed at different radius

旋翼桨尖速度不变的情况下，旋翼升力不随飞行速度改变。也就是说，在一定范围内，桨尖速度和升力是一一对应的。飞行速度增加，虽然桨叶相对气流速度增加，但是气流迎角却减小，这是因为在速度增大的情况下要保持桨尖速度不变，桨盘迎角（轴倾角）必须相应减小，导致桨叶气动力变化很小，因此总升力基本不变。

2.3 旋翼总距影响

一般旋翼机的旋翼总距（安装角）很小，主要是出于旋翼转速不能太低的考虑[14]，因为一定拉力时，总距越大转速越小。

旋翼拉力随总距增大而增大，如图3 所示，在旋翼半径为1.6 m，桨尖速度为120 m/s 的情况下，总距从0°增加到2°，旋翼拉力从270 N 增加到370 N 左右。

旋翼轴倾角随总距增大而减少，在桨尖速度为120 m/s、飞行速度为22.22 m/s 的情况下，2°总距对应的轴倾角为7.7°，1°总距对应的轴倾角为8.8°，0°总距对应的轴倾角为10.1°，如图4 所示。

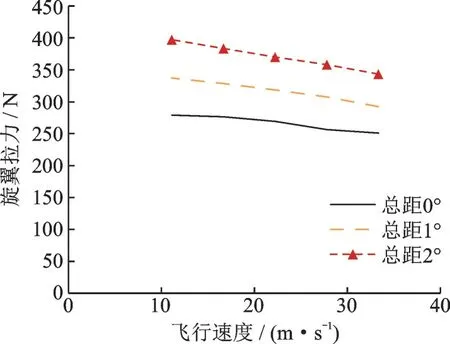
图3 不同总距下的旋翼拉力随飞行速度变化曲线Fig.3 Rotor thrust varying with fight speed at different collective pitch

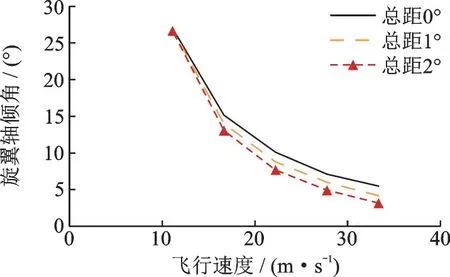
图4 不同总距下的旋翼轴倾角随飞行速度变化曲线Fig.4 Rotor shaft angle varying with fight speed at different collective pitch

假设旋翼拉力恒定为250 N，则总距主要影响转速。如图5 所示，随着总距增加，所需要的旋翼转速降低，半径为1.6 m 的旋翼总距为0°时转速为700 r/min 左右，总距2°时转速为600 r/min 左右。而且旋翼半径越大，旋翼转速越低。

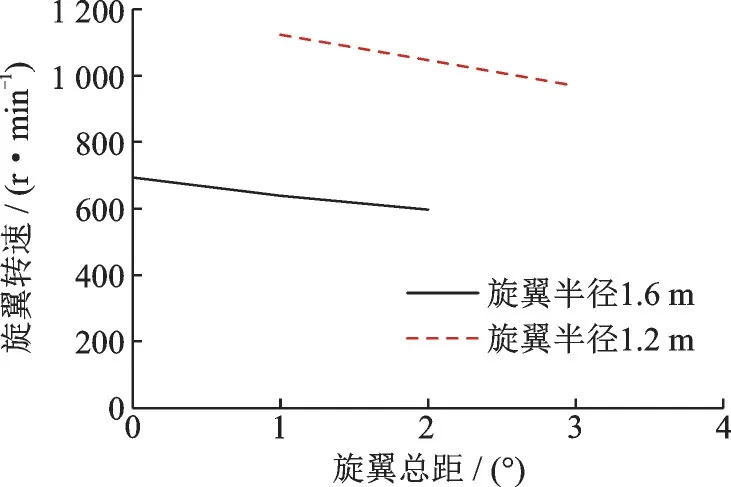
图5 旋翼转速与总距关系曲线Fig.5 Relationship between rotation speed and collective pitch

旋翼总距较大时，小飞行速度下难以保持平衡，这说明随着总距增大，维持较小的桨尖速度需要的最小气流速度（飞行速度）增大。即在一定的总距下需要达到一定的飞行速度，旋翼才能维持自转，这就是自转旋翼机旋翼总距一般较小的原因。

2.4 旋翼轴倾角操纵

旋翼机通过控制轴倾角以适应不同飞行状态，得到需要的旋翼拉力[15]。旋翼轴与机体连接，通过一套拉杆机构可以操控旋翼轴倾斜角。为得到相同的旋翼拉力，飞行速度增加时，需要减少旋翼轴倾角，同时旋翼转速保持不变；当飞行质量降低时，需要减少轴倾角（旋翼转速同步减少），从而稳定飞行状态。

如图6 所示，在旋翼半径为1.4 m，总距为1°的情况下，小转速时的轴倾角小，旋翼拉力也小。桨尖速度从100 m/s 提升到140 m/s，旋翼拉力增加约160 N，轴倾角降低2.5°～12.5°，大速度时降低量小。轴倾角操纵量不能太大，否则旋翼后倒太多容易与机身尾面发生碰撞。

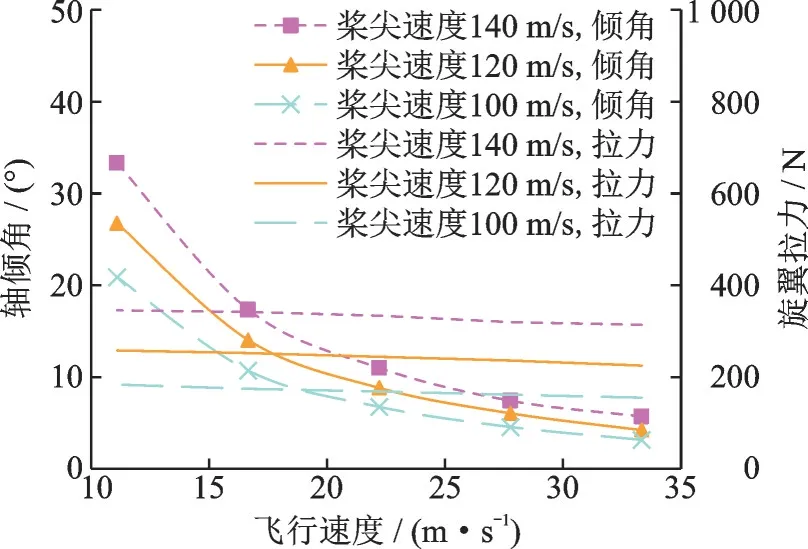
图6 旋翼轴倾角与旋翼拉力随飞行速度变化规律Fig.6 Rotor shaft angle and thrust versus flight speed

飞行速度减小时，要保持桨尖速度ΩR不变（也就是升力不变），则桨盘迎角（对应轴倾角）必须增大，但桨盘迎角不应过大（一般不超过20°），这就对最小飞行速度提出了限制要求。

3 旋翼机试验

3.1 试验设备与模型

试验在直流式开口低速风洞（图7）进行，试验段尺寸为8 m×6 m，最大风速为55 m/s。机身通过撑杆安装到支架上，采用布置在机身内部的应变式天平测量得到试验件六力素。

研制的无人旋翼机（称为“试验机”）旋翼半径为1.5 m，风洞试验时试验件包括旋翼、旋翼轴罩（旋翼与机身之间的整流罩）及机身（不含机翼、尾翼、推进桨）。试验时旋翼轴与机身之间的倾斜角保持3°不变，通过调节机身迎角实现旋翼轴倾角的控制。试验风速范围为10～30 m/s，升力L 垂直于风向向上，阻力D 与来流风向一致。

图7 风洞试验设施Fig.7 Wind tunnel test facility

3.2 独立机身试验

首先拆除桨叶，进行机身吹风，得到机身气动特性。如图8 所示，机身阻力随机身迎角增加而略有增加，受风速变化的影响较大，风速越大阻力越大。风速为30 m/s、迎角为2.92°时，机身阻力为40.42 N。

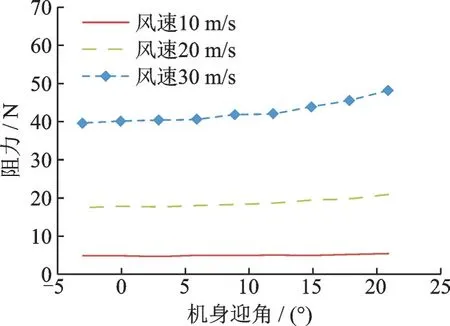
图8 不同风速下机身阻力随机身迎角变化规律Fig.8 Fuselage drag varying with angle of attack at differ-ent wind speed

把阻力折算到阻力系数

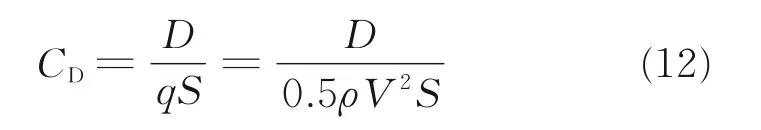
阻力系数随机身迎角增大而增大，平均值在0.062 左右（图9）。小风速时测量结果略有波动，主要是由于风洞气流在小速度时不稳定。

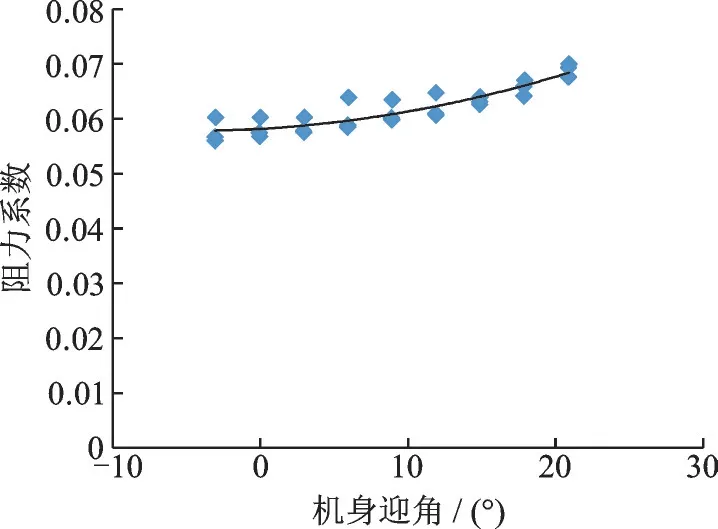
图9 机身阻力系数随机身迎角变化曲线Fig.9 Fuselage drag coefficient versus angle of attack

当机身迎角为正（抬头）时，机身一般产生正升力。如图10 所示，机身迎角增大，机身升力随之增大。风速为30 m/s 时，机身迎角由0°增加到20.9°，机身升力由4 N 增加到28.8 N。风速越大，升力越大。

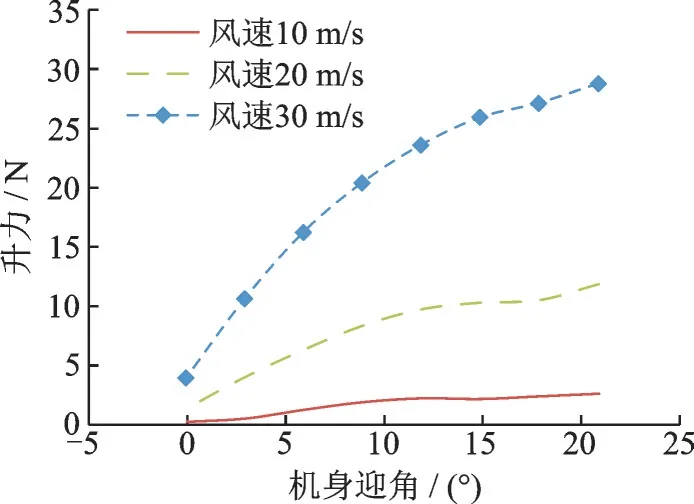
图10 不同风速下机身升力随机身迎角变化曲线Fig.10 Fuselage lift varying with angle of attack at different wind speed

3.3 机身+旋翼试验

在机身吹风完成后，为获取旋翼气动力，在机身桨毂上安装旋翼桨叶，对“机身+旋翼”组合体进行吹风试验。试验中旋翼为自转状态，受气流驱动旋转，并无其他动力驱动。旋翼总距保持0°不变，机身+旋翼组合体测试数据减去独立机身测试数据，就可以得到旋翼数据。升力向上为正，阻力与来流方向一致，为风轴系下结果，作用点在桨毂中心。

由于旋翼升力明显大于机身升力，因此机身+旋翼组合体升力与旋翼升力差别很小。如图11 所示，旋翼升力随轴倾角的变化非常明显，轴倾角越大升力越大。这说明操纵旋翼轴倾角，可以直接控制旋翼升力大小，实现旋翼机的爬升或下降。风速为30 m/s 时的升力明显大于风速为20 m/s 时的升力，而且，风速为30 m/s 时升力随轴倾角的变化斜率更大。这说明，随着飞行速度增大，若轴倾角不变旋翼升力增大，为了保持升力不变需要减少旋翼轴倾角，大速度时操纵旋翼轴倾角更加敏感。

阻力方面，除了机身部分产生阻力外，旋翼也产生阻力，其主要是由旋翼轴向后倾斜造成。如图12 所示，旋翼阻力随着轴倾角增大而增大，相同轴倾角时风速为30 m/s 时的阻力明显大于风速为20 m/s 时的阻力。

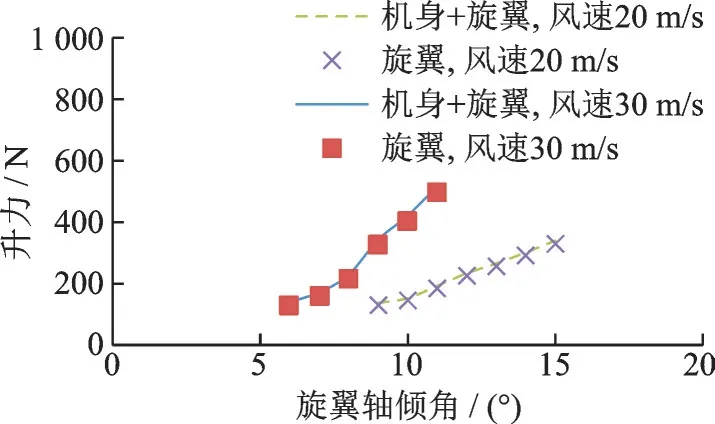
图11 旋翼机升力随轴倾角变化规律Fig.11 Gyroplane lift versus rotor shaft angle

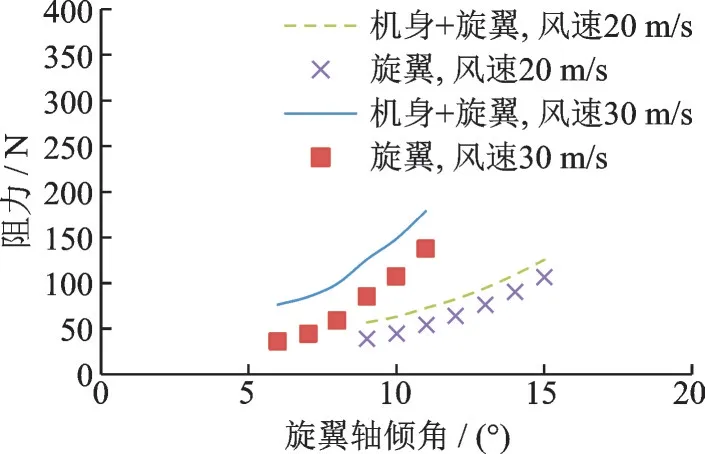
图12 旋翼机阻力随轴倾角变化规律Fig.12 Gyroplane drag versus rotor shaft angle

旋翼升力与阻力的比值，即升阻比，可以表示旋翼前飞时的气动效率。升阻比随飞行速度增大而增大，试验中最大升阻比为3.83（图13）。

3.4 与计算结果对比

对旋翼升力和阻力进行矢量合成，得到旋翼拉力

应用上述建立的旋翼气动模型，计算得到与试验状态相对应的旋翼拉力，通过操纵旋翼轴倾角进行旋翼配平（需用功率为0）。如图14 所示，计算结果与试验结果趋势一致，数值吻合性好。飞行速度为20 m/s 时需要操纵轴倾角至11.5°左右，才能达到试验机所需要的旋翼拉力。

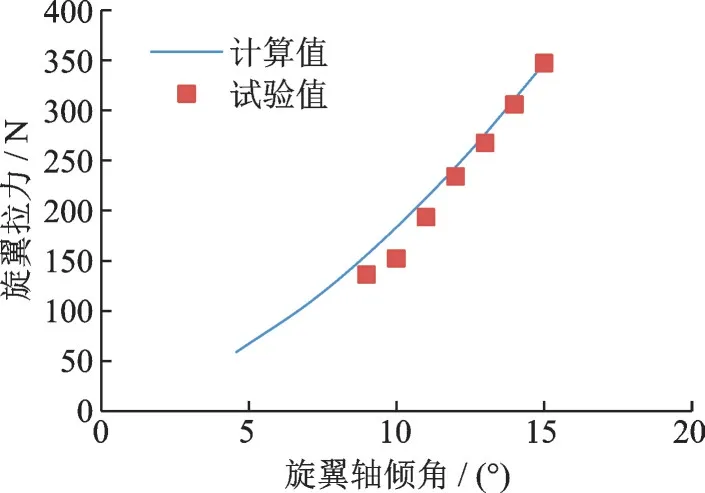
图14 旋翼拉力计算值与试验值对比Fig.14 Comparison of calculated results with experimental data for rotor thrust

4 旋翼拉力公式

根据以上分析，旋翼拉力除了跟旋翼设计方案紧密相关外，还跟飞行状态有关。本文试验机的旋翼拉力可以拟合成以下方程表示

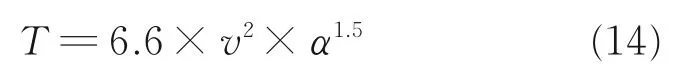
式中：v 为飞行速度，α 为轴倾角。从式（14）可以看出，旋翼拉力与飞行速度的平方成正比，与轴倾角的1.5 次方成正比关系。也可以说，在保持旋翼拉力不变的情况下，飞行速度的平方与轴倾角的1.5次方成反比例关系，这对飞行控制律设计具有重要指导作用。

对式（14）进行推广，可以写成

式中：E 为常数项，它取决于旋翼设计方案和飞行环境。F 为轴倾角指数，不同旋翼方案F 取值不同，它跟旋翼翼型及桨距角相关。R 为旋翼半径，σ为实度，ρ 为大气密度，θ 为桨距安装角，f 为系数。

以半径1.2 m，实度0.045，桨距角1°的旋翼方案为算例，对拉力式（15）进行验算。系数e=17，f=10，于是E=4.2，F=1.3，此旋翼拉力公式为

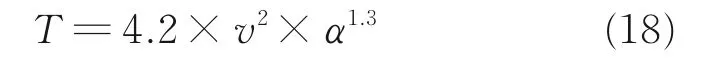
应用本文建立的旋翼气动模型对半径1.2 m旋翼方案进行不同状态下的拉力计算，并与式（18）计算结果进行对比，如图15 所示，两者数值接近，吻合性好。

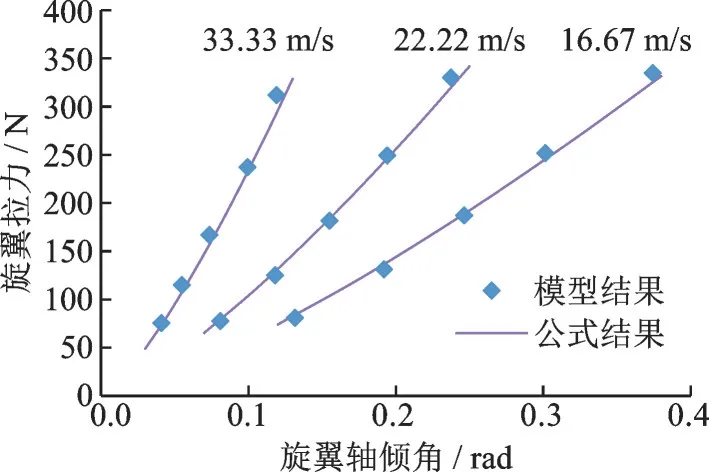
图15 不同方法得到的旋翼拉力对比Fig.15 Comparison of rotor thrust by different methods

5 结 论

本文针对无人旋翼机，建立了旋翼气动力计算与试验方法。通过旋翼气动特性的对比分析，可以得出以下结论：

（1）当旋翼半径增大时，旋翼轴倾角不变，旋翼拉力增大。当旋翼总距增大时，旋翼拉力随之增大，旋翼轴倾角减少。旋翼机的旋翼总距一般很小，在0°附近。

（2）旋翼机通过控制轴倾角，以适应不同飞行速度，速度越大轴倾角越小，以保持所需要的旋翼拉力。旋翼转速随着飞行速度基本不变，不同飞行重量对应不同转速，旋翼转速需要保持在合理范围内（桨尖速度100～180 m/s）。

（3）试验机的机身阻力和升力，随风速增大而增大，随迎角增大而增大。旋翼升力明显大于机身（无机翼）升力，轴倾角越大升力越大，旋翼阻力主要是由旋翼轴向后倾斜造成。

（4）旋翼拉力跟设计方案、飞行状态和操纵相关。对于本文研制的无人旋翼机方案，稳定平飞时旋翼拉力与飞行速度的平方、轴倾角的1.5 次方成正比关系。