阻力伞附加质量与阻力系数修正方法

孙建红，孙 智，王从磊，余元元,4，侯 斌，房 明

（1.南京航空航天大学飞行器环境控制与生命保障工信部重点实验室，南京210016；2.南京航空航天大学民航学院，南京211106；3.航空工业宏光空降装备有限公司，南京210022；4.航空工业航宇救生装备有限公司航空防护救生技术航空科技重点实验室，襄阳441003；5.中车南京浦镇车辆有限公司，南京210031）

阻力伞是辅助高速飞行器着陆的一类降落伞，主要应用于飞机，可使其着陆滑跑距离缩短30%～40%[1]。因其良好的气动减速性能，阻力伞已发展为飞行器减速着陆过程的重要设备。在阻力伞设计和研究过程中，目前主要通过试验和数值仿真的方法来获取其相关气动性能。其中试验方法作为阻力伞性能获取的一种重要手段已被广泛采用，然而在阻力伞试验过程中，特别是滑车阻力伞系统试验过程中，由于阻力伞系统在做非匀加速度的非定常运动的同时会受到前置体尾流场的影响[2-3]，现有的阻力伞试验数据分析方法往往难以准确计算其阻力系数。但是，阻力系数作为阻力伞性能评估的重要参数，其计算结果的精确性至关重要。因此，有必要针对阻力伞试验过程中的这些影响因素进行研究，建立更为准确的阻力伞阻力系数计算方法。

阻力伞的试验研究方法主要包含风洞试验、滑车试验以及飞机试验等。与风洞试验中的定常流修正不同，在阻力伞滑车和飞机试验过程中，系统往往在做非匀加速/减速的非定常变速运动，即存在明显的非定常特性[4]。在非定常因素分析研究中，相关学者常采用附加质量方法反映非定常运动的力和力矩。文献[5]中最早提出附加质量的概念，并详细叙述了在水中进行振荡圆球的阻力实验时发现圆球的非定常阻力与它所挟带的流体质量有关，即圆球具有附加质量后较它的真实质量更大。之后广大学者对其进行了大量的试验以及工程计算等方面的研究。在试验方面，文献[6]研究了浸没在液体中的钟摆的运动，并且提出将物体所增加的附加质量用物体同体积的流体质量的n 倍来表示。随后，文献[7]对附加质量与振幅相关性展开了实验研究。在对“猎户座”飞船降落伞研制的过程中，美国科学家也对开伞过程中附加质量的变化进行了理论建模与风洞试验，从而提高了对降落伞附加质量的计算精度[8]。2017 年，陈光皓[9]通过一系列关于垂直柱体管状结构（圆柱、方柱、平板）在空气及不同液体（包括水和15 号液态石蜡油）中的自由衰减振动实验，对附加质量作用与不同柱体形状、自身旋转角度以及液体特性（密度、黏度）的关系进行了研究。2018 年，王在铎等[10]提出了一种通过水下模态试验获取结构附加质量系数及时变阻尼比的方法，依据该方法开展试验模型设计及干、湿模态试验，得到了典型圆柱结构刚体平动、转动及一阶弯曲的附加质量系数。另一方面，针对物体变速运动问题，1960 年，文献[11]中提出了一种计算任意三维物体势流的方法(Hess-Smith方法），通过求解方程组源密度分布，进而求解流场内任意点的速度、压力等物理量。文献[12-14]先后采用Hess-Smith 方法对水下艇体在流体中运动的附加质量进行计算，分析了附件质量对艇体的影响，从而为水下艇体的附加质量计算提供了一种有效的方法。

近年来，随着计算流体力学及计算机技术的快速发展，数值计算方法逐渐成为研究流体运动问题的重要工具，例如马烨等[15]采用CFD 对简单外形物体的匀变速运动进行数值模拟，并根据其受力方程得到物体六自由度运动情况下的附加质量。李刚等[16]针对球体、椭球体和某型深潜器的附加质量采用数值和试验的方法进行了测定，发现数值计算方法只有在黏性流模型下才能得到可靠的结论。傅慧萍等[17]采用CFD 和动网格技术对两种回转体外形的附加质量进行了数值计算。Wang 等[18]分析了有黏流情况下与法向加速度有关的气动力系数和俯仰阻尼力与力矩系数，从而提高这些气动系数的估算精度。张光法[19]采用CFD 方法对“海豚”半潜式航行体不同潜深和附加质量之间的关系进行了数值计算分析。周景军等[20]提出了一种水下航行体附加质量高精度、高效的数值计算方法。El-gabaili 等[21]利用CFD 软件对平面圆伞充气过程附加质量的变化进行了计算。姚保太等[22]采用数值模拟方法和动网格技术计算了在黏性不可压流体中圆球做变加速运动时的附加质量、阻力和阻力因数，并研究了在管体域中圆球变加速运动对附加质量、阻力和阻力因数的影响。冯双双等[23-24]采用流体计算软件及动网格技术，计算得到了不同边界情况下物体的附加质量。张晓强等[25]针对跨介质运动物体出水过程和入水过程的时变附加质量问题，提出了一种快速有效的计算策略。刘智丽等[26]对采用CFD 方法计算了有黏流情况下椭球体在时变来流速度下的气动特性，发现有黏流的轴向附加质量和无黏流中的结果有较大的差异。

对于降落伞和阻力伞，其过程涉及流固耦合复杂过程[27-28]，对应的附加质量的计算也更复杂，工程上一般通过对模型适当简化来进行计算。目前，国内外学者大多是结合降落伞充气过程的特点提出相应的工程计算方法，包括阻力面积计算法、内含质量计算法以及充气半径计算法等。阻力面积计算法的计算精度取决于阻力面积和参考系数的准确度，方便利用实验数据进行修正；但对于有收口控制的降落伞，充气过程中由于存在阻力面积的阶跃变化，从而按照此方法计算开伞载荷时附加质量的求导结果会出现突变，最终反映到开伞载荷的计算结果中很可能会出现不合理的增大[29]。内含质量计算法需要基于势流理论计算表观质量，目前是假设取等体积椭球体的计算结果，可能导致产生较大的误差，目前通过实验也难以获取降落伞的表观质量，其计算结果难以修正，但该方法不需要获取实验数据，对于缺乏实验数据的新伞型可用此方法作为参考[30]。充气半径计算法的计算误差主要取决于降落伞充气体积的计算误差及参考系数的选取误差，由于通过实验确定充气体积较为复杂，因此对该方法的计算结果进行实验修正虽然可行但也较为复杂[31-32]。这些方法在降落伞计算过程中也得到了应用。邢小军等[33]基于降落伞充气面积和充气半径引起的附加质量公式，建立了降落伞充气阶段的数学模型，并研究了其充气过程载荷的主要影响因素。蔡志军等[34]注意到了阻力伞阻力特性的差异性，并基于大量数据，采用统计学方法给出了阻力伞载荷大小和方向分布规律。

目前，在关于阻力伞的研究中，一般采用工程计算方法来对其阻力系数进行计算，但是由于阻力伞系统在做非匀加速度的非定常运动并受前置体尾流场的影响时，现有的这种阻力伞试验数据分析方法往往难以准确计算出其阻力系数。因此，本文针对阻力伞试验的这种非定常和尾流干扰特性，对阻力伞系统进行了动力学分析，并对阻力伞非定常运动过程中的附加值和尾流场特性进行了理论分析，提出了阻力伞非定常修正和动压修正方法，建立了阻力伞系统的阻力系数修正模型，为阻力伞设计和试验研究提供参考。

1 附加质量模型与修正方法

当物体在不可压缩的理想流体中做变速运动时，即使是理想的无黏流体，其物体表面上的流体压力的总矢量R 依然不等于0。所以变速运动的物体会有一个额外的阻力，这个压力的总矢量R 即为流体的惯性阻力，它通常与加速度方向相反。

所以，当物体在外力F 作用下，在理想流体中做变速运动时，物体的动量方程可写为

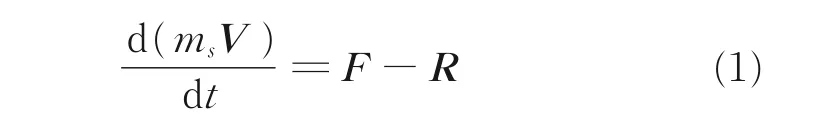
式中：ms表示物体的质量，V 表示物体的运动的速度矢量。这里流体的惯性阻力可以看成是物体吸附的流体跟随物体一起运动而产生的额外阻力，即吸附的质量为mf的流体随物体一起做变速度运动，因此可以将流体的惯性阻力R 写成动量的形式

将式（2）代入式（1）可以得到

由式（3）可以看出，当物体在流体中做变速度运动时，在质量上添加了一个额外的部分，这部分流体的质量mf被称为“附加质量”，一般附加质量的大小由物体的形状和运动参数决定。也可以把这种运动模态称为“双质量模型”，即物体在流体中运动时，质量可包含物体本身质量以及物体包裹质量或者物体运动影响的质量（附加质量）两部分。两部分质量可以看成两个质点，因此也可以称为“双质点模型”，如图1 所示。当物体匀速运动时，附加质量为零，即mf=0。

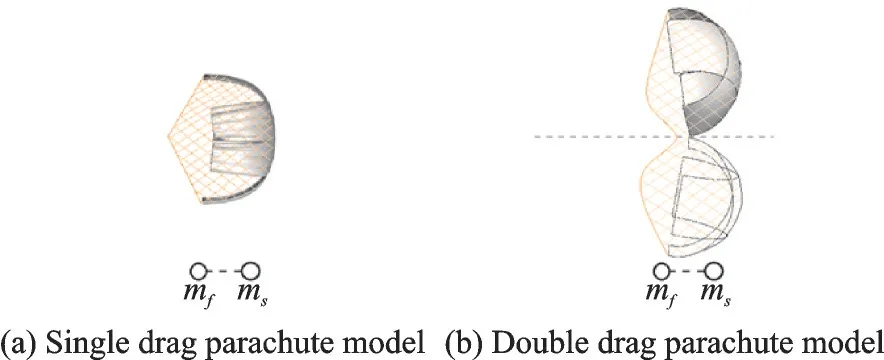
图1 阻力伞双质量模型示意图Fig.1 Dual mass model of drag parachute

根据势流理论，这种额外的惯性阻力可以通过物体包裹质量或者物体运动影响的质量（附加质量）来衡量。在简单构型的实心球体实验中，得出的流体惯性对球体阻力系数的影响如图2 所示。由图2 可知，当物体运动速度很大，且加速度和尺寸很小时，由流体黏性而引起的阻力占主导地位；而当物体运动速度很小，加速度和尺寸很大时，克服周围流体惯性产生的阻力占主导地位。所以，在阻力伞系统研究中，由于阻力伞自身质量较小，且其包裹的空气质量和它自身质量处于同一量级，因此对于阻力伞的变速度工作过程需要分析流体惯性对阻力伞气动性能的影响，即需要同时考虑伞质量和流体质量的双质量影响。

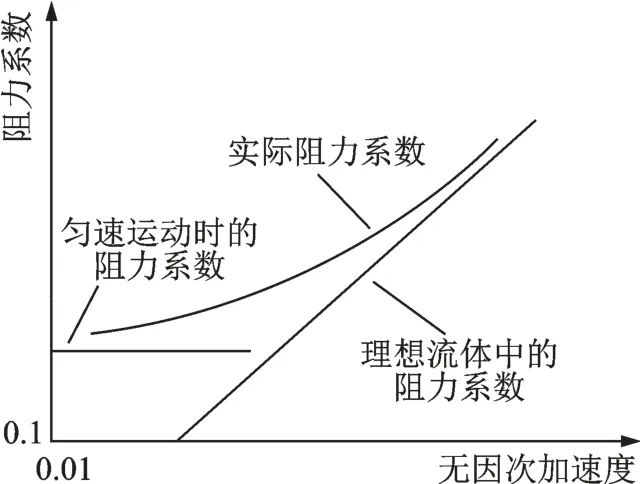
图2 阻力系数与无因次加速度的关系[4]Fig.2 Relationship between drag coefficient and accel-eration[4]

在阻力伞工作过程中，阻力伞在运动方向上的动力学方程为

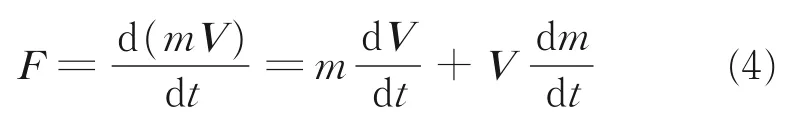
对于阻力伞的工作过程，阻力伞处于张满状态，其伞衣包裹了大量的空气，并且部分空气跟随阻力伞一同做非匀加/减速度运动，同时由于阻力伞自身质量较小，伞衣包裹空气质量与其自重相当，不能忽略。因此，可以将阻力伞的运动过程看成阻力伞自身和跟随阻力伞一起运动的空气两部分共同运动组成。根据图1 所示的“双质量模型”，阻力伞系统的质量由阻力伞自身的质量ms和其包裹的流体质量mf两部分组成，所以式（4）可以转换为

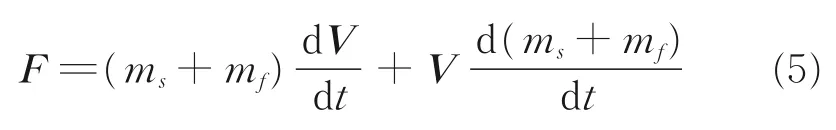
通常情况下，阻力伞自身的质量ms为一常数，所以式（5）可写为

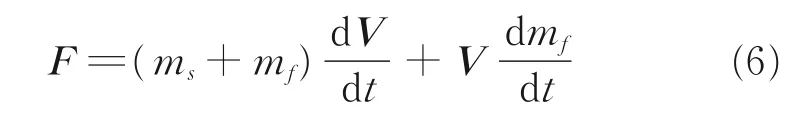
当阻力伞工作过程为充气过程时，其包裹的流体质量mf会随着伞衣的充气而增大；当阻力伞处于充满以后的稳定工作阶段时，其包裹的流体质量mf可以近似认为保持不变，所以对于阻力伞充满状态，式（6）可以简化为

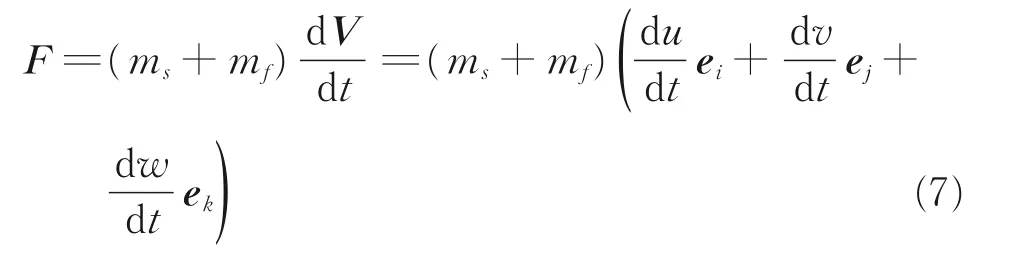
式中：ei,ej,ek分别为i,j,k 方向的单位向量。

在阻力伞滑车试验以及阻力伞工作过程中，其主要沿来流方向做变速度运动，因此式（7）可以简化为

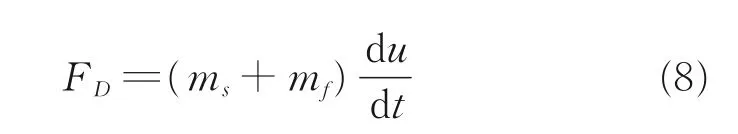
而对于考虑非定常影响的充满状态的阻力伞，根据阻力伞“双质量模型”，流体质量可以假设为伞衣呈现的半球形加一段截锥形的理想形状所包裹的空气质量，因此可以将阻力伞的附件质量mf表示为

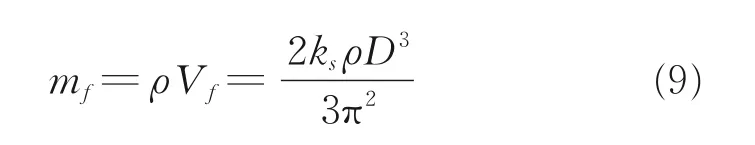
式中：ρ 为空气密度，Vf为伞衣包裹空气体积，D 为充满状态阻力伞直径。ks为伞型系数，当阻力伞为圆形阻力伞时，ks=1；阻力伞为十字型阻力伞时，ks＜1。

在阻力伞工作过程中，其直径不易测量，通常情况下采用阻力面积（迎风面积）A 作为反映伞衣阻力特征的参考量，不同来流速度情况下，A 也有所不同，并且阻力面积也是影响开伞动载的主要因素，在阻力伞性能分析和研究中，通常以此作为特征参数，因此式（8）可写成阻力面积的函数表达式

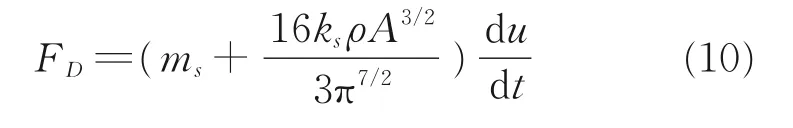
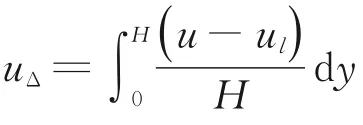
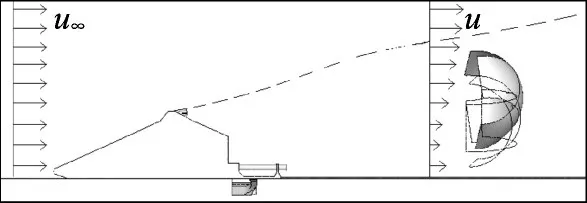
图3 阻力伞前置体尾流场示意图Fig.3 Wake field of front body of drag parachute

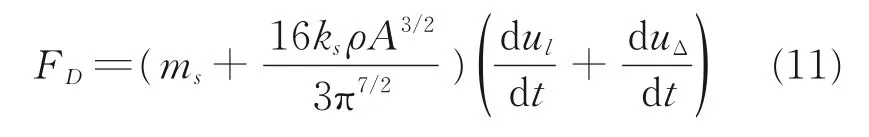
将式（11）表示的阻力代入阻力伞阻力系数计算公式，可以得到非定常、尾流动压损失影响下的阻力伞阻力系数公式为

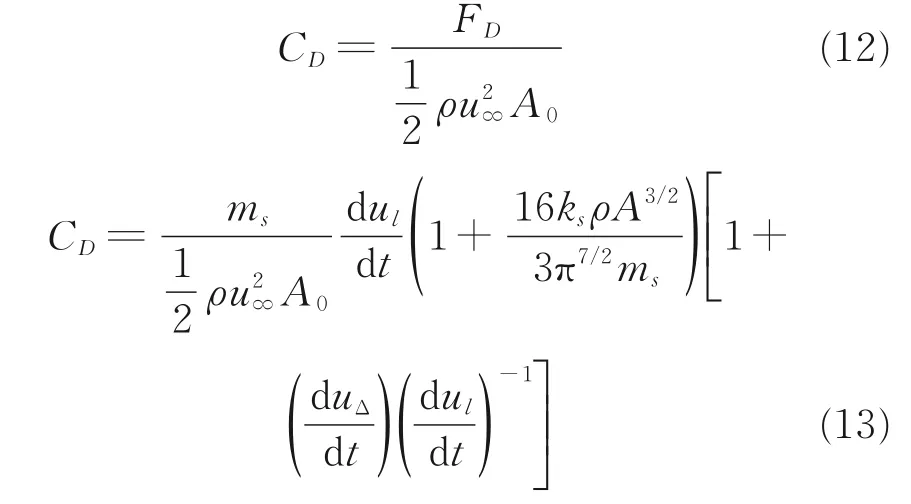
式中：A0为阻力伞名义面积。对于物体匀速运动时，不考虑非定常影响，此时其包裹的流体由于惯性随着阻力伞一起运动，此时附加质量mf=0。若阻力伞无尾流场影响时，阻力伞流场的速度即为自由来流速度u=ul，此时阻力伞所受到的力可表示为

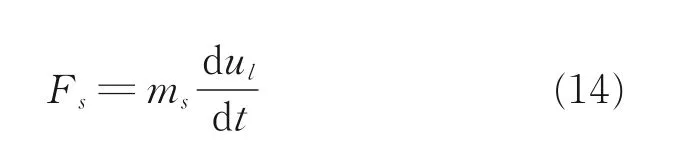
为了方便分析与计算，引入非定常修正系数ε和动压修正系数ξ，则阻力伞阻力伞系数公式可以简化为

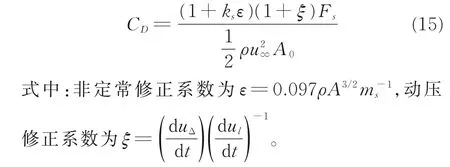
2 不同伞型阻力伞计算与分析

以滑车阻力伞系统试验为例，试验的滑车模型如图4 所示，选取两种阻力伞进行试验，A 型十字形单伞模型和B 型十字形双伞模型。试验过程中，阻力伞从伞筒弹出并迅速充满，阻力伞充满后滑车阻力伞系统做加速度变化的变减速运动。考虑到该过程中阻力伞做变速运动，因此采用本文提出的附加质量模型及修正方法对其进行分析研究。

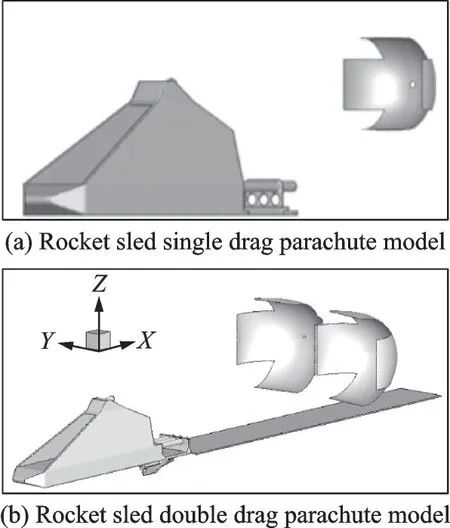
图4 滑车阻力伞系统模型Fig.4 Rocket sled drag parachute system

2.1 A 型单伞

首先对A 型十字型单伞进行分析研究，其充满状态下的单伞模型如图5 所示。根据十字型伞的张满尺寸确定本试验十字形伞的伞型系数ks取0.90，其试验及稳态仿真结果如表1 所示。

图5 A 型单伞模型Fig.5 A-type single drag parachute model

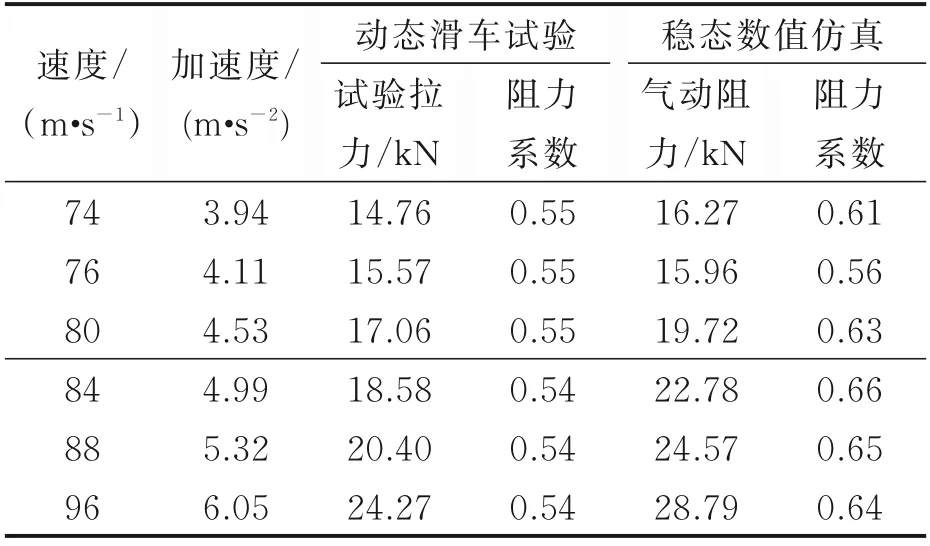
表1 不同工况下A 型单伞动态滑车试验与稳态仿真结果Table 1 Dynamic rocket sled test and steady‑state simula‑tion results of A‑type single drag parachute under different conditions

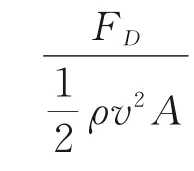
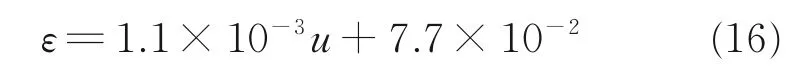
图6 A 型单伞非定常修正系数随来流速度的变化Fig.6 Nonsteady correction coefficient changing with incoming flow velocity of A-type single drag parachute

通过前面的理论分析可知，影响阻力伞阻力特性计算的主要因素除了非定常特性以外，还有前置体尾流的动压差异影响。接下来对滑车阻力伞系统的尾流场动压差异影响进行分析。由图7 可以看出，前置体滑车的存在，使得滑车后方存在一定的低速区，这种影响会使得阻力伞工作区域（通常为滑车后方1.5H～2.0H 的区域）内的流体动压降低，从而影响阻力伞气动性能的测量结果。

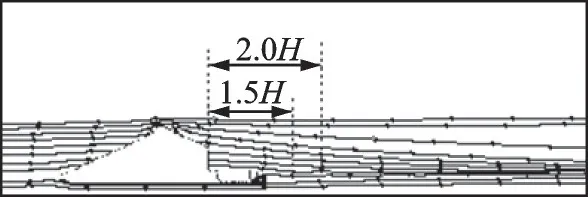
图7 滑车数值模拟中心对称面上的流线分布Fig.7 Streamline distribution on center symmetry plane of numerical simulation of rocket sled

为了更清楚地分析前置体滑车带来的动压损失对阻力伞的影响，分别对定常状态下不同速度的滑车阻力伞系统和自由边界阻力伞的气动阻力进行数值仿真计算，结果如表2 所示。

通过两者的对比，根据ξ= F FD-1 求出动压修正系数ξ，其中F 为自由边界条件下的阻力伞气动力，动压修正系数ξ 计算结果如图8 所示。通过对有无前置体滑车结果的对比分析，建立动压修正系数ξ 的量化关系式为

表2 不同状态下的A 型单伞系统气动阻力Table 2 Aerodynamic resistance of A‑type single drag parachute under different conditions

图8 A 型单伞动压修正系数随来流速度的变化Fig.8 Dynamic pressure correction coefficient changing with incoming flow velocity of A-type single drag parachute

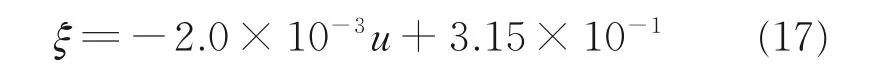
对于该十字形阻力伞，其阻力伞气动阻力系数修正公式为

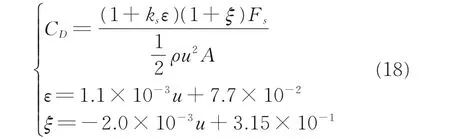
式中：ks=0.90。

为了进一步验证阻力伞附加质量及其修正方法的准确性，采用得到的单伞阻力系数修正式（16）对第3 组试验结果进行分析，并将计算结果与单伞阻力伞系数设计值（风洞试验自由边界修正结果）进行对比，结果如表3 和图9 所示。从图9 中可以看出，随着运动速度的变化，阻力伞的阻力系数在小范围内振荡，其大小趋于一定值。通过原始工程计算方法与本文修正方法的对比可以看出，原始工程计算方法得到的阻力系数与阻力伞风洞试验结果差异较大，差异最大可达27%；而本文提出的修正方法得到的阻力系数与设计值相对误差较小，总体上误差小于9%。这主要是因为阻力系数原始工程计算方法没有考虑附加质量（非定常特性）和动压损失对阻力系数的影响，而本文基于附件质量的修正方法包含了非定常特性修正系数ε 和动压修正系数ξ，能够较好地反映非定常特性和动压损失对阻力系数计算值的影响。因此，本文建立的阻力伞附件质量修正方法能够更准确地计算阻力伞系统试验中的阻力伞真实阻力系数。

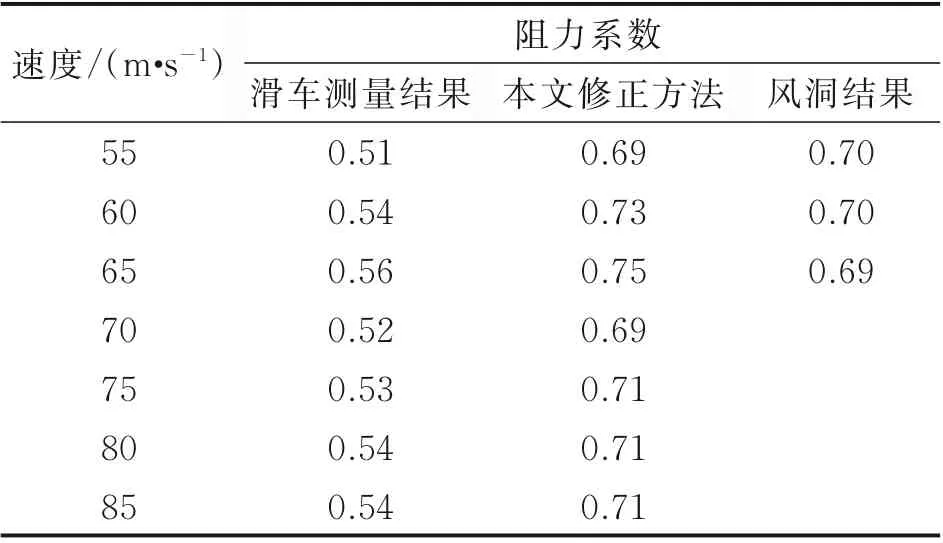
表3 A 型单伞阻力系数分析对比Table 3 Results of drag coefficient of A‑type single drag parachute

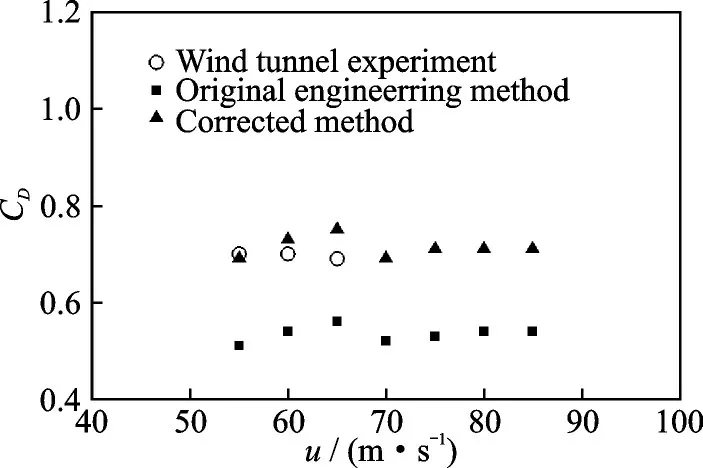
图9 A 型单伞阻力系数修正结果对比Fig.9 Comparison of drag coefficient results of A-type sin-gle drag parachute by different methods

2.2 B 型双伞

通过对单伞的分析研究可以发现，本文提出的基于附加质量的阻力伞修正方法可以更准确地计算阻力伞的阻力系数。进一步，针对双伞进行研究以验证本文阻力系数修正方法在双伞上的适用性。选取B 型十字形双伞作为研究对象，其充满状态下的几何外形如图10 所示。与A 型单伞相比，B 型双伞只是尺寸不同，因此B 型双伞的伞型系数ks同样取0.90。B 型双伞的试验结果如表4 所示。

图10 B 型双伞模型Fig.10 B-type double drag parachute model

表4 不同工况下B 型双伞动态滑车试验与稳态仿真结果Table 4 Dynamic rocket sled test and steady‑state simula‑tion results of B‑type double drag parachute un‑der different conditions

在对阻力伞单伞系统进行研究的基础上，进一步对滑车双阻力伞系统进行研究，研究方案与单伞系统相似。首先，对稳态不同来流条件下滑车阻力伞系统进行数值模拟，采用对伞衣表面流体作用进行面积分的方法，得到阻力伞的气动阻力，从而计算出其阻力系数。另一方面，采用最小二乘法对试验的拉力值进行数据降噪处理，计算出滑车双伞系统的试验阻力特征值，并与定常模拟结果对比，计算结果如表4 所示，进而求出非定常修正系数ε，结果如图11 所示。通过对比分析，建立非定常修正系数ε 的量化关系式为

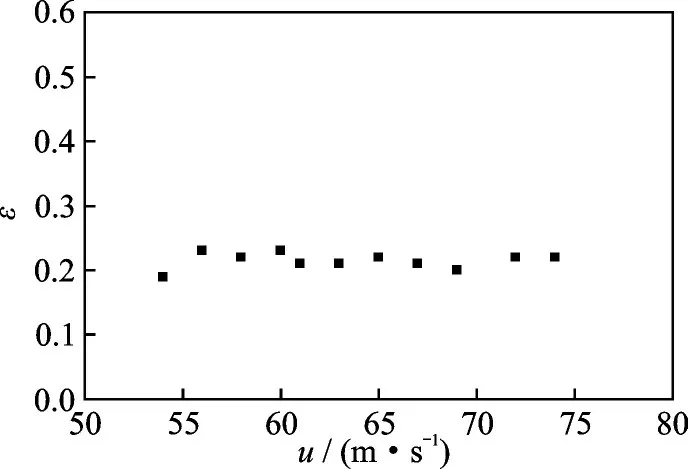
图11 B 型双伞非定常修正系数随来流速度的变化Fig.11 Nonsteady correction coefficient changing with incoming flow velocity of B-type double drag parachute

进一步，为了研究前置体滑车带来的动压损失对双伞的影响，同样分别对定常状态下不同速度的滑车阻力伞系统和自由边界阻力伞的气动阻力进行数值仿真计算，结果如表5 所示。通过两者的对比求出动压修正系数ξ（如图12 所示），并建立前置体滑车双伞动压修正系数ξ 的量化关系式为

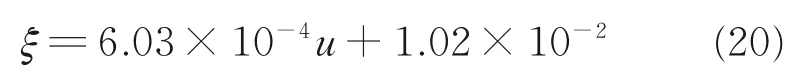
所以该十字形双伞系统阻力伞气动阻力系数修正公式为

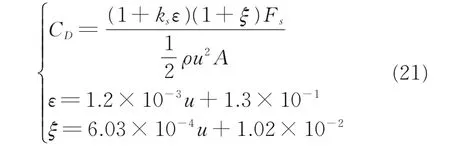
式中：ks=0.90。

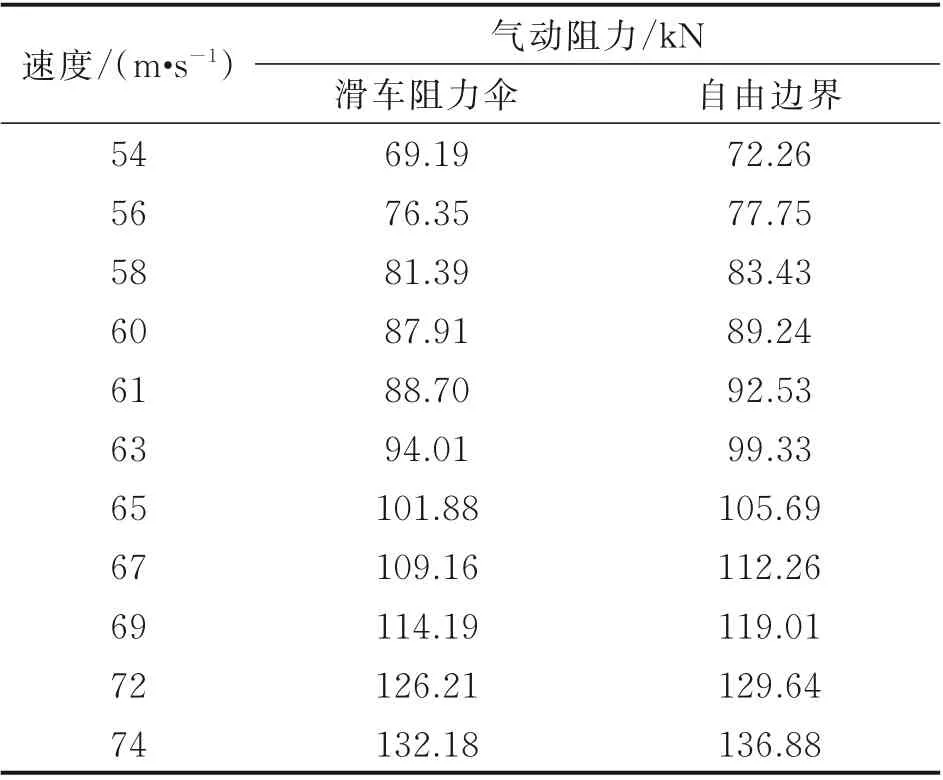
表5 不同状态下的B 型双伞系统气动阻力Table 5 Aerodynamic resistance of B‑type drag para‑chute under different conditions

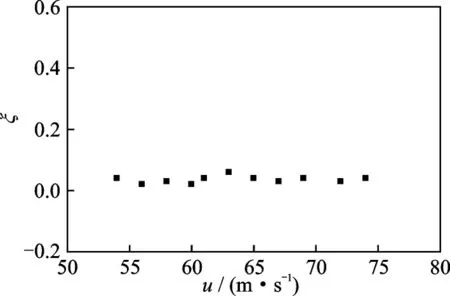
图12 B 型双伞动压修正系数随来流速度的变化Fig.12 Dynamic pressure correction coefficient changing with incoming flow velocity of B-type double drag parachute

为了进一步验证阻力伞附加质量及其修正方法的准确性，采用得到的双伞阻力系数修正式（19）对第5 组试验结果进行分析，并将计算结果与双伞阻力伞系数设计值（风洞试验自由边界修正结果）进行对比，结果如表6 和图13 所示。从图13 中可以看出，随着运动速度的变化，双伞阻力伞的阻力系数在小范围内振荡，其大小趋于一定值。通过原始工程计算方法与本文修正方法的对比可以看出，原始工程计算方法得到的阻力系数与双伞风洞试验的结果差异较大，差异最大可达30%；而本文提出的修正方法得到的阻力系数与设计值相对误差较小，总体上误差小于7%，并且速度越大，误差越小。这主要是因为滑车阻力伞系统试验中，运动速度大时，加速度值也大，因而阻力伞系统的非定常特性就越明显，附件质量修正的结果就越好。同时，运动速度越大，滑车尾流场动压损失越大，对阻力系数计算值的影响也越大。阻力系数原始工程计算方法没有考虑附加质量（非定常特性）和动压损失对双伞阻力系数的影响，而本文提出的双质量模型阻力系数修正方法包含了非定常特性修正系数ε 和动压修正系数ξ，能够较好地反映出非定常特性和动压损失对阻力系数计算值的影响。因此，本文建立的阻力伞阻力系数修正方法能够更准确地计算阻力伞系统试验中的阻力伞真实阻力系数。

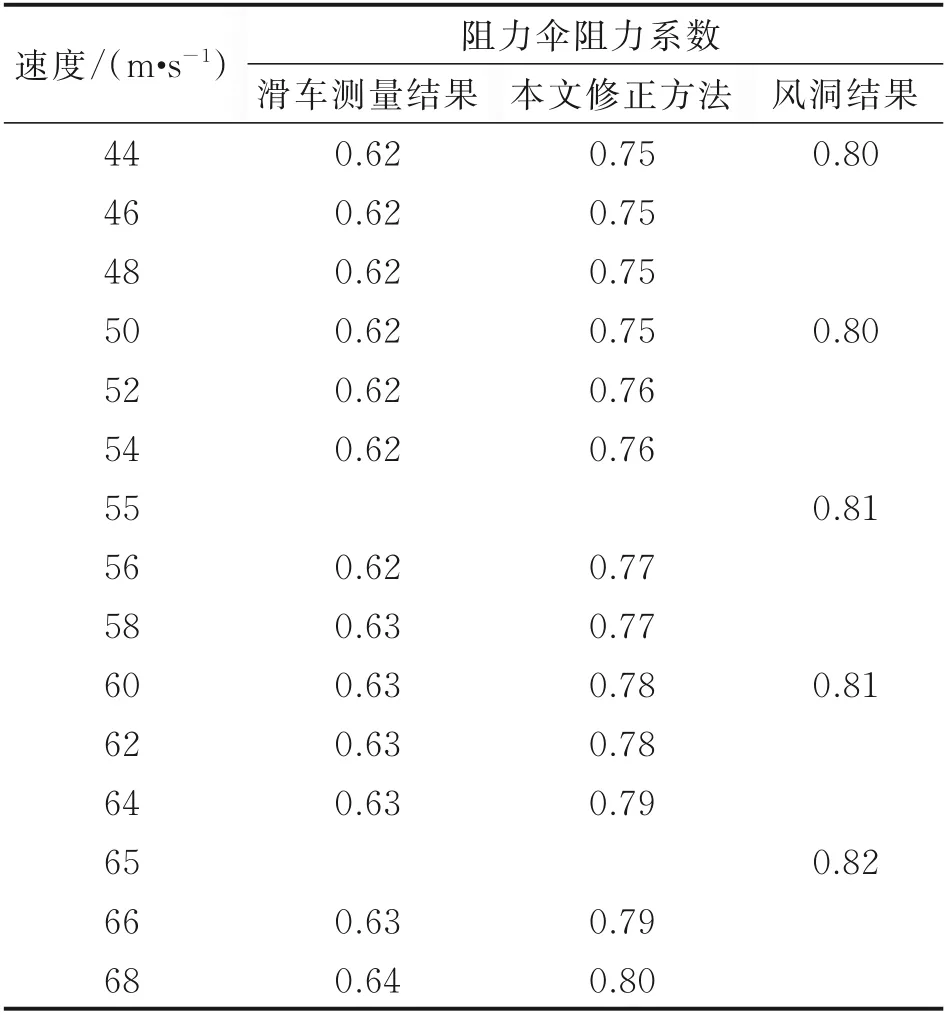
表6 B 型双伞阻力系数分析对比Table 6 Results of drag coefficient of B‑type double drag parachute

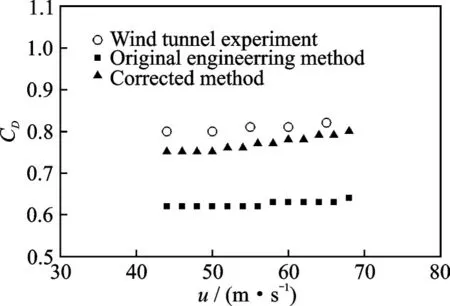
图13 B 型双伞阻力系数修正结果对比Fig.13 Comparison of drag coefficient results of B-type double drag parachute by different methods

3 结 论

本文针对阻力伞试验结果与风洞试验的差异性，对阻力伞试验过程中阻力伞系统进行了动力学分析，并对试验中的非定常附加质量和前置体动量损失进行了理论研究，在此基础上，提出了双质量模型，并建立了阻力伞阻力系数非定常修正和动压修正方法。采用本文提出的阻力系数修正方法对某型十字形单伞和双伞模型的试验结果进行了分析，确定了该阻力伞相应的非定常修正系数和动压修正系数，建立了对应的阻力伞阻力系数修正数学模型，并将计算结果与风洞试验和传统计算方法结果进行了对比。结果表明：对于单伞模型，本文计算方法可以使得计算结果误差从原来的27%降低到9%以内；对于双伞模型，本文计算方法可以使得计算结果误差从原来的30%降低到7%以内。综上可见，本文提出的阻力系数修正方法能够更准确地计算阻力伞的阻力系数，从而为阻力伞试验数据分析提供了一种更准确的计算方法。