基于粒子群优化的直升机飞行控制律设计方法
2021-05-06刘松源靳秋硕朱元希
刘松源,吴 伟,靳秋硕,朱元希
(南京航空航天大学直升机旋翼动力学国家级重点实验室,南京210016)
直升机作为一种高阶并且具有强耦合特性的旋翼飞行器,其操稳特性对控制律的设计有很强的依赖性,对控制系统的性能提出了十分复杂的要求,这就导致了直升机飞行控制律设计难度大,控制效果不理想等问题。20 世纪60 年代以来,随着现代控制理论的飞速发展,针对直升机设计的自适应控制、鲁棒控制等先进控制方法的研究有了长足进展,在理论研究上取得了很大的突破[1-2],但受到实际计算能力限制以及理论本身的复杂性,现代控制理论目前还较难应用于真实直升机。
最优控制理论中的线性二次型调节器(Linear quadratic regulator,LQR)经过多年发展,已经可以通过求解状态反馈矩阵对控制系统的参数配置作出有效指导,经其设计的闭环系统可根据调整权矩阵Q、R 改变系统的动态响应,并且经该方法计算得到的控制参数具有相当的工程指导价值。目前国内外对基于最优控制理论的直升机控制律设计方法还处于发展阶段,有学者对加权矩阵参数对实际响应的影响进行分析后提出了有指导意义的参数调整策略,但该调整方法仍然局限于单一飞行器,且并没有解决过于依赖经验的问题[3]。基于各种优化算法改进的LQR 控制器设计方法也已经有了很多相关成果,但基本上对象都为低阶并且解耦的简单系统,如倒立摆以及模拟电路开关的控制问题,这类模型的共同点是输入向量和状态量均较少,且耦合问题不严重,因此其反馈结构也更为简单。但对于直升机这类高阶耦合系统,因为其丰富的输入输出关系,导致其状态反馈矩阵有相当大的维度,让该类设计方法还没有得到有效验证,而这也是本文开展该方向研究工作的目的。在面向直升机系统进行设计时,应用LQR 设计控制律面临的问题主要包括权矩阵的取值过于依赖工程经验,且需要花费大量时间人为调整[4],高阶系统的全状态反馈会极大增加运算负荷,因此LQR 控制器的权矩阵参数优化方法也是近年来优化算法领域的热点关注问题[5-7]。
针对权矩阵的参数选取问题,本文采用粒子群优化算法结合LQR 控制器与直升机动力学特性,设计合理的优化指标,进行对Q 矩阵的多参数同步优化,取优化结果中的主状态反馈组成部分作为直升机飞行控制律。在此基础上,对样例直升机进行了飞行控制律设计,并对闭环系统的带宽与相位延迟、时域响应做了分析。
1 直升机飞行控制律基本架构
1.1 直升机开环操稳特性分析
本文采用UH-60A 作为样例直升机进行控制系统的设计,该对象本身为非线性、非定常的六自由度动力学模型。LQR 控制器名义上是针对线性系统进行反馈设计,因此分析模型采用UH-60A 在海平面悬停状态配平后进行小扰动线性化的状态空间模型,其表达式为
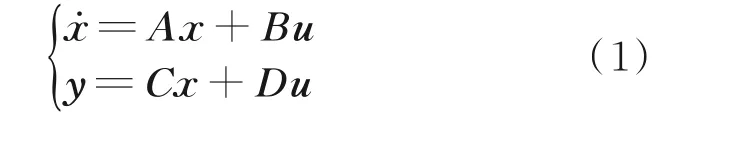
式中
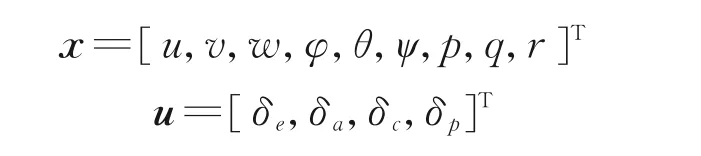
式中:x 为状态向量,x 中各状态量依次为直升机体轴系下x、y、z 三轴方向的速度,俯仰角、滚转角、航向角以及绕三轴的角速度;u 为输入向量,依次为纵向周期变距、横向周期变距、总距以及尾桨总距;y 为输出量,是状态量和输入量的线性组合;A 和B分别为相对应状态量的气动稳定导数矩阵与对应输入的操纵稳定导数矩阵,C 和D 为适维矩阵[8]。
由文献[9]中提供的状态矩阵A,可得到直升机开环特征值如表1 所示。

表1 直升机开环特征值及对应模态Table 1 Helicopter open‑loop characteristic values and corresponding modes
一组正实部的共轭复根代表了纵向振荡模态,主要由于飞行速度和俯仰角不稳定性导致,在悬停模式下,该模态是不稳定的,长时间的悬停会使驾驶员感到疲劳[10]。以纵向单通道为例,对其状态空间模型进行拉氏变换,得到俯仰角对纵向周期变距的传递函数为
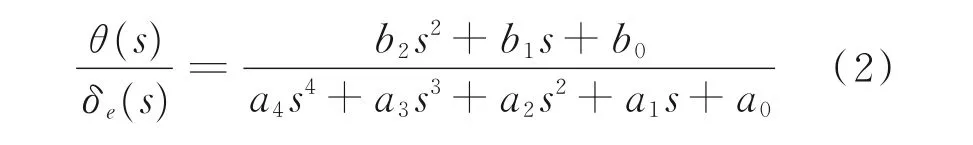
操纵机构的传递函数可等效为一个二阶系统,两者之积即为俯仰角对操纵杆的传递函数。根据ADS-33E-PRF 对悬停低速模式下的飞行品质定义,直升机带宽取相位带宽与增益带宽的较小值,根据传递函数计算得到纵向与横航向的带宽分别为0.989 与2.63 rad/s,分别处于飞行品质等级2 以及飞行品质等级1 规定区域[11]。纵向通道带宽较低说明驾驶员在驾驶过程中需要花费大量精力抑制不稳定模态,极大增加了驾驶负荷,横向带宽虽然满足飞行品质等级1 的要求,但是在考虑直升机有严重纵横向耦合的特性下,纵向通道的不稳定性也会大大降低横向通道的实际响应效果,因此需要通过控制系统对其飞行品质进行优化。
1.2 直升机基本飞行控制律
根据对直升机开环操稳特性的分析,为优化系统稳定性,增加闭环系统轴间解耦能力,改善系统动特性并提高飞行品质[12],根据系统输入特性,建立如式(3)所示的直升机基本增稳飞行控制律,有
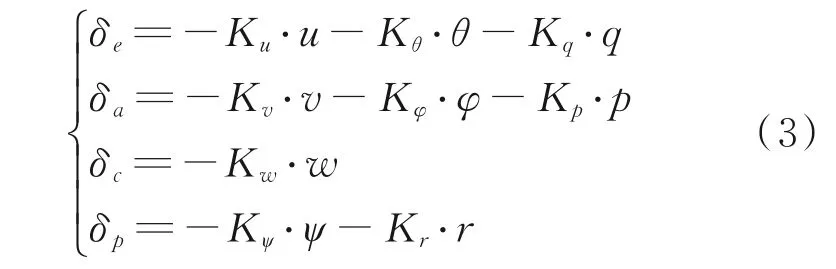
式中系数均为对应输入的状态量反馈值,以Ku为例,其物理意义为状态量u 反馈到输入端的比例系数。经LQR 控制器设计后得到,而消减其他经LQR 控制器设计得到的反馈值对闭环系统影响的方法将根据粒子群优化算法给出。
2 引入粒子群优化算法的改进LQR设计方法
2.1 基于LQR 的直升机控制参数设计
经过LQR 控制器设计的闭环系统,动态特性原则上表现为当状态不为零或系统受到扰动时,状态量将快速回归平衡点。为了使控制系统能够有效跟随指令输入,将状态向量进行拓展,引入速度与航向角的误差信号,定义指令输入
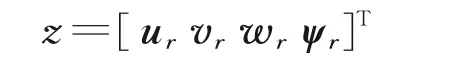
则误差为
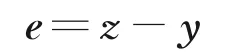
考虑指令为定值信号,取误差量的微分
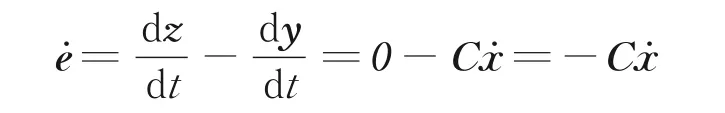
建立扩展状态空间模型为
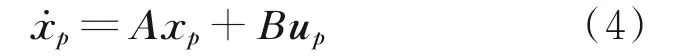
式中

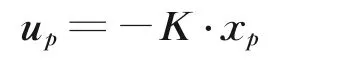
则u=-Kx⋅x-Ke⋅e/s。
搭建闭环系统模型如图1 所示。从图中可以看出,状态反馈矩阵Kx旨在改变系统稳定性与动态性能,而误差反馈矩阵Ke赋予状态量对指令的良好跟踪性能[13]。动态响应效果将在仿真结果中给出。
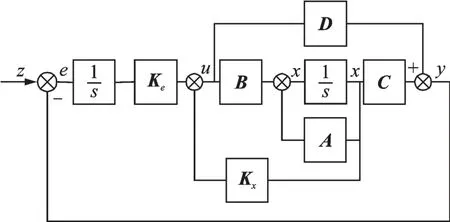
图1 闭环系统模型结构图Fig.1 Model structure of closed-loop system
2.2 权矩阵质量评价函数
权矩阵的参数选取应使求解得到的全状态反馈矩阵接近于主状态反馈结构,LQR 控制器的两个权系数矩阵Q 和R,分别影响状态量响应特性与输入幅值,考虑输入限幅方法的多样性,对R 矩阵的取值无需专门做出要求,因此本文只针对Q 矩阵进行参数优化,在这里取R 为适维单位矩阵,取
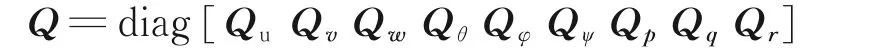
式中各参数决定相应状态量的响应速度,数值越大,相应的状态量响应速度越大,反馈系数越高。Q 矩阵系数将作为粒子对结果进行寻优。经LQR方法设计得到的状态反馈矩阵形式为
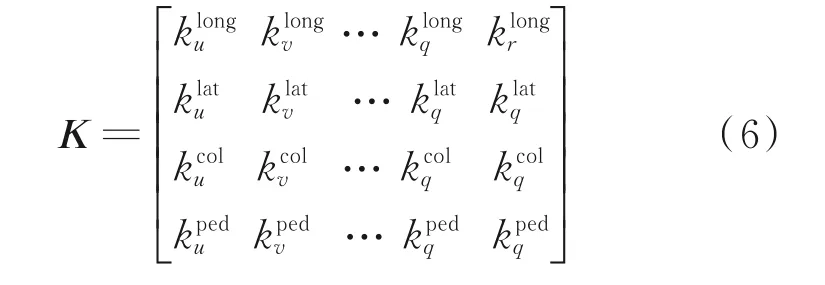
对于一般的増稳系统而言,较为理想的反馈结构为
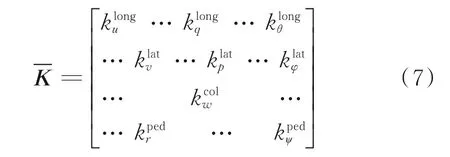
可以看出,该反馈结构按照输入输出特性对状态量进行分通道比例式反馈,相比于全状态反馈具有物理意义清晰、结构简单和便于调整的优点。而通过LQR 计算得到的是式(6)所示的反馈结构,下面讨论通过对加权矩阵进行参数优化从而使K逼近。
为了实现加权矩阵Q 的优化,本文定义如式(8)所示的权矩阵质量评价函数,有
JQ=I1⋅Mlong+I2⋅Mlat+I3⋅Mcol+I4⋅Mped(8)式中I 为权重,可根据具体需求进行调整,M 为单通道主变量占比的倒数平方和,单通道质量评价函数如下
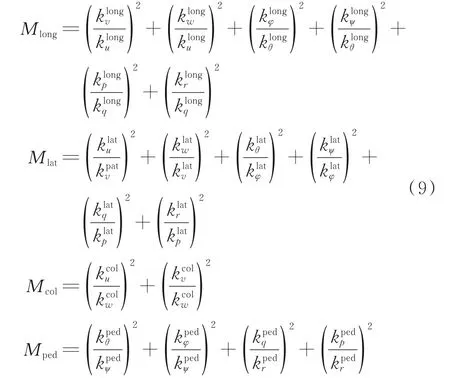
权矩阵质量评价函数作为粒子群优化算法的指标函数,寻优结果即为JQ到达最小值时线性二次调节器矩阵Q 的取值情况,根据最优控制原理可以解得相应的状态反馈矩阵K,此时K 中的元素呈现主操纵反馈参数占比相对极大的特性,即根据直升机的操纵特性完成了理想的控制参数设计。
2.3 基于粒子群算法的权矩阵优化
假设在Q 维空间中有m 个粒子,其中粒子i 的位置为xi=(xi1,xi2,xi3,…,xiQ),粒子i 的移动速度为vi=(vi1,vi2,vi3,…,viQ);假设在粒子i 的搜索历史中,其最优位置为pi=( pi1,pi2,pi3,…,piQ),而在所有m 个粒子的搜索历史中,最优位置为pg=( pg1,pg2,pg3,…,pgQ)。则 粒 子i 的 第d 维 元 素 的 标准粒子群算法的迭代公式(粒子位置速度更新公式)可表示为
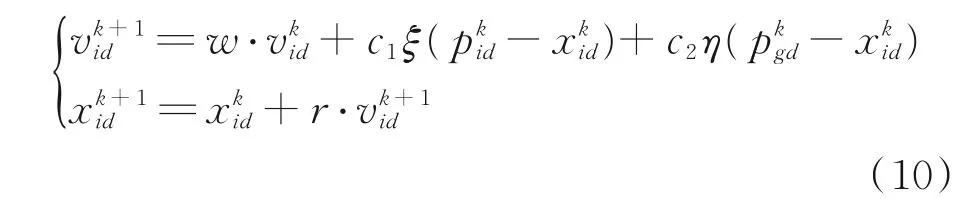
式 中:k 为 迭 代 次 数;w 为 惯 性 权 重;c1和c2为 学 习系数;ξ、η 为0 到1 区间均匀分布的随机数;r 为粒子速度的约束因子;i = 1,2,…,m;d = 1,2,…,Q。式(10)表明算法中各粒子以指标函数最小为准则,进行自身以及群体的最优位置迭代,从而对式(8)所示指标函数数值(算法中称为适应度)进行优化。
粒子群算法具有可调参数少、收敛速度快和方便理解和实现等特点,是一种并行寻优的群体迭代算法。作为一种模拟鸟群觅食的启发式智能优化算法,现已广泛应用于多目标优化、分类和决策等方面[14]。
根据上述的设计对象、质量评价函数,使用粒子群优化算法进行权矩阵参数设计的具体步骤如下:
(1)初始化。在定义空间Rn中产生一个种群Q(t) =diag([QuQvQwQθQφQψQpQqQr],对 于本文而言,初始种群为随机取值的对角矩阵,式中Qu,…,Qr为LQR 控制器中对应各状态量的Q 矩阵系数;随机产生各粒子的初始速度V(t) =(VQ1,…,VQ9)。
(2)评价种群Q(t)。引入适应度计算公式,计算每个粒子在每一维空间的适应度。
(3)迭代寻优。比较当前粒子适应度与历史最佳适应度pbest,如当前值更优,则pbest替换为当前值;比较个体适应值与种群最佳适应度gbest,如个体值更优,则gbest替换为当前个体值。
(4)位置速度更新。适应度对比更新后,根据式(10)更新粒子的速度与位移,产生新的种群Q(t+1) 。
检查结束条件,若满足条件,则结束优化并给出结果,不满足则t=t+1 并返回(2),直至计算达到最大迭代次数n。结束条件通常情况下给定最大迭代次数或最高精度要求(一般为适应度阈值),因寻优上限未知,本文中方法未设置精度要求,仅以最大迭代次数作为结束条件。
3 直升机飞行控制律设计过程与闭环系统分析
3.1 基于改进LQR 方法设计直升机飞行控制律
本文中粒子群算法参数取c1、c2值皆为1.5。粒子速度的约束因子取值为1。惯性权重w 取0.8,种群规模取100,最大迭代次数取200。经上述优化算法过程,权矩阵质量评价函数收敛结果如图2 所示。从图中可以看到,作为优化指标的权矩阵质量评价函数在进行30 次左右迭代计算后已经基本收敛,整个计算过程耗时8 s,具有相当高的寻优效率,与此同时得到权矩阵的优化结果为
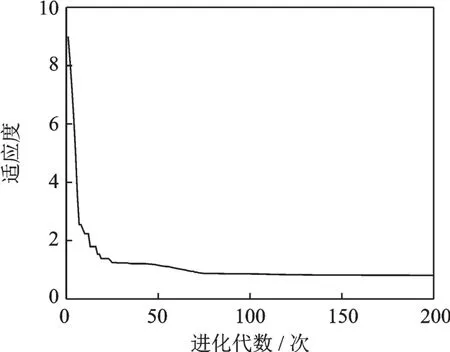
图2 粒子群算法寻优过程与收敛结果Fig.2 Optimization process and convergence results of par-ticle swarm optimization
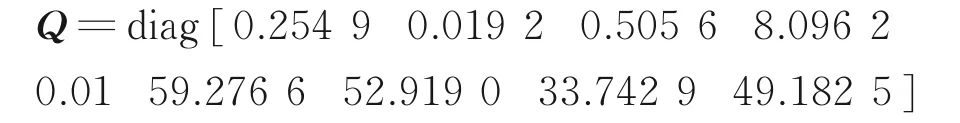
将权矩阵代入式(4)所示指标函数,求解式(11)所示的黎卡提方程,有
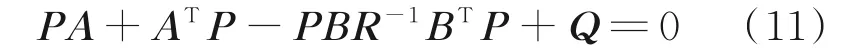
则可以得到反馈系数矩阵

在反馈系数矩阵中选取主状态反馈参数代入式(3),从而得到飞行控制律设计结果如表2所示。
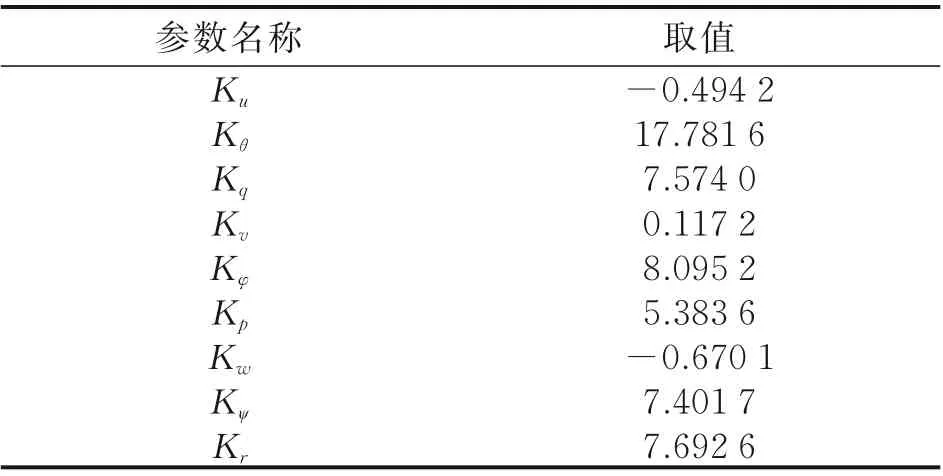
表2 控制参数的具体取值Table 2 Value of control parameters
3.2 直升机闭环系统性能分析
3.2.1 面向飞行品质的直升机带宽与时间延迟分析
由于本文的分析对象是UH-60A 直升机在悬停点进行配平的小扰动线性化模型,因此根据旋翼飞行器飞行品质规范ADS-33E-PRF,对于小幅度/中低频时系统动特性要求和小幅度/高频时系统的带宽和相位延迟作飞行品质分析。
经过状态反馈后的纵向单通道状态空间模型为
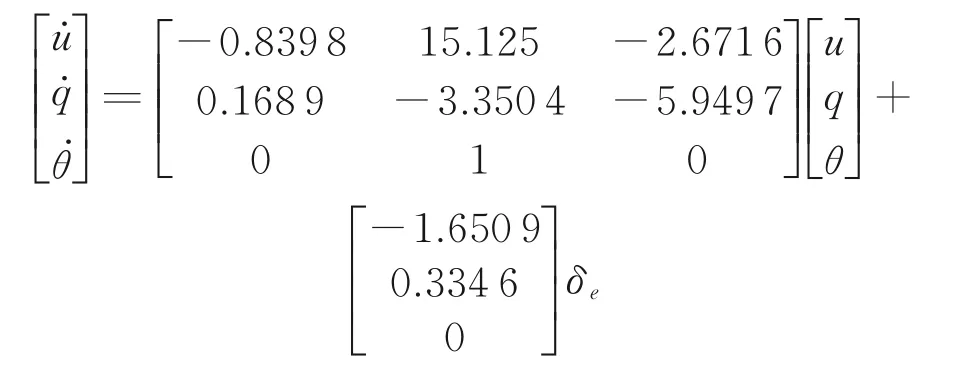
俯仰角对纵向周期变距的传递函数为
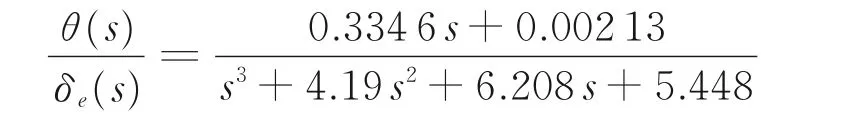
作动器传递函数模型取自文献[15],即有
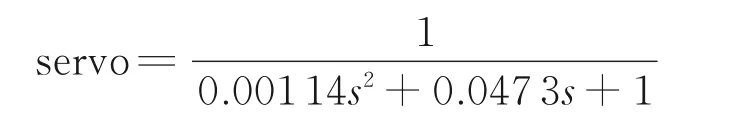
两者串联,构成俯仰角对纵向操纵杆的传递函数,其伯德图如图3 所示。

图3 俯仰角传递函数伯德图Fig.3 Bode diagram of pitch angle
ADS-33E-PRF 中定义相位为-135°时的频率为相位带宽,ω180幅值的上6 dB 处为增益带宽,两者取其小即为直升机带宽,从图3 中可以看出,经过控制器之后ωBWθ(纵向通道带宽)达到了4.08 rad/s,经 计 算 得 到 相 位 延 迟τpθ=0.039 18 s,达到飞行品质等级1 的同时还保留了一部分裕量。
经过状态反馈的横航向通道状态空间模型为

滚转角对横向周期变距的传递函数为
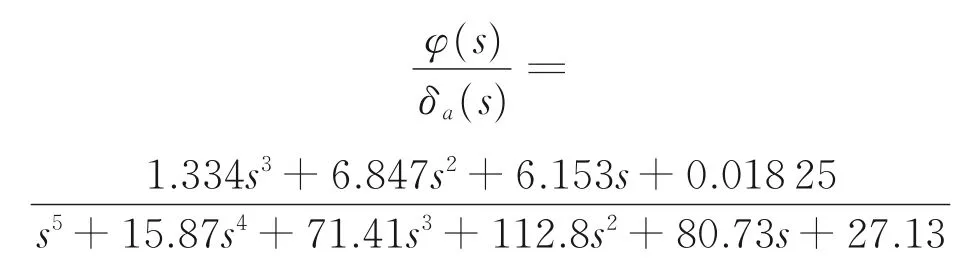
经过相同的作动器传递函数模型,得到滚转角对横向操纵杆的传递函数伯德图如图4所示。图中经比较后取横向通道带宽ωBWφ=6.85 rad/s,远大于飞行品质等级1 中关于滚转角的带宽要求。计算得到该函数相位延迟τpφ=0.039 49 s,满足飞行品质要求。

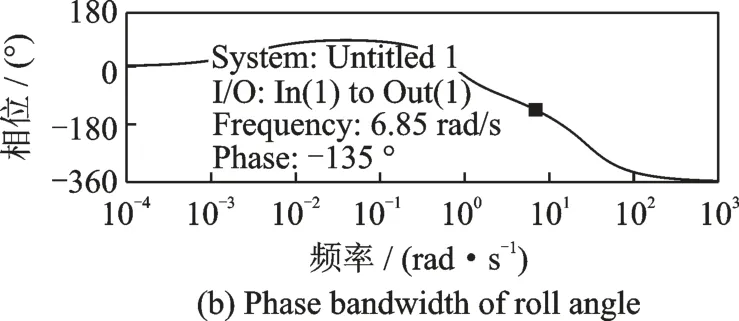
图4 滚转角传递函数伯德图Fig.4 Bode diagram of roll angle
同理得到航向角对脚蹬传递函数伯德图如图5 所示。经比较后取ωpψ=4.36 rad/s,计算航向操纵相位延迟τpψ=0.039 82 s,同样具有优秀的动态性能。

图5 航向角传递函数伯德图Fig.5 Bode diagram of yaw angle
经过状态反馈后的垂向单通道模型为
ẇ=-5.601w-7.921δc
垂向速度对总距操纵的传递函数为
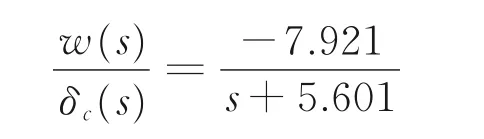
飞行品质规范中并没有给出垂向通道的频域指标,但要求在悬停或低速前飞状态下,垂向速度对总距操纵的响应在5 s 之内有大致的一阶形状,垂向通道时域响应如图6 所示。输入为单位阶跃信号,代表总距杆的单位变量,因为总距杆的速度响应与规定的机体轴坐标系方向相反,因此响应为负值,从图6 中可以看出,响应在1 s 时已经基本达到稳态值,完全满足垂向通道的时域要求。
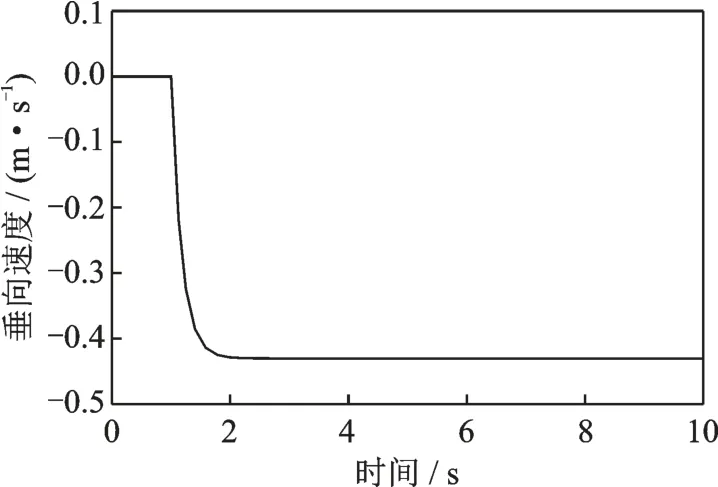
图6 垂向速度w 单位操纵响应Fig.6 Step response of vertical velocity w
3.2.2 直升机飞行控制律时域响应分析
为验证本文控制参数设计方法的合理性,根据1.2 节中所示控制系统设计方法搭建仿真模型,对速度指令的跟踪性能以及通道间解耦能力进行分析,仿真模型如图7 所示。
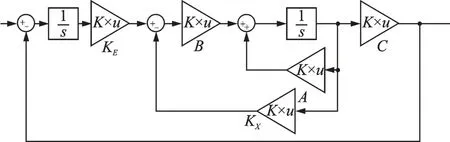
图7 直升机闭环系统仿真模型Fig.7 System simulation model of helicopter closed-loop
输入输出分别为三轴速度与航向角的指令即响应。以纵向速度为例,给定10 m/s 的速度指令,主通道速度响应如图8 所示。其他通道速度响应如图9 所示。
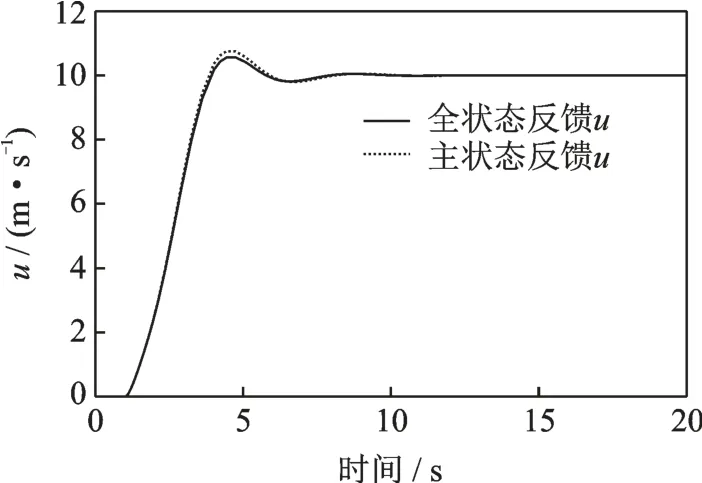
图8 纵向通道对前飞速度指令的响应Fig.8 Longitudinal channel response to forward flight speed command
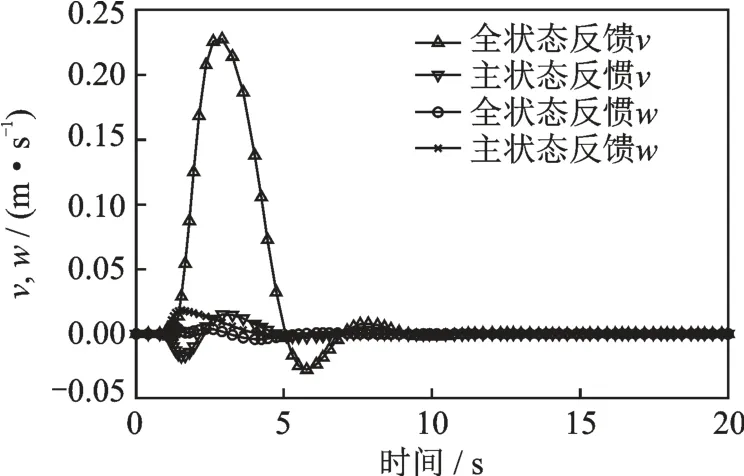
图9 横向与垂向速度对前飞速度指令的响应Fig.9 Transverse and vertical velocity response to forward flight speed command
从图8~9 中可以看出,经过本文方法设计的控制系统,对指令具有优良的跟踪性能,并且拥有足够的通道间解耦能力,除纵向速度u 之外的其他两轴速度被抑制在0 附近并迅速收敛。同时可以发现本文中采用的主状态反馈系数构成的闭环系统与其相对应的全状态反馈系统在动态性能上十分接近,其中对横向速度v 的抑制稍次于全状态反馈,但对垂向速度w 的抑制要优于全状态反馈,航向角响应如图10 所示。
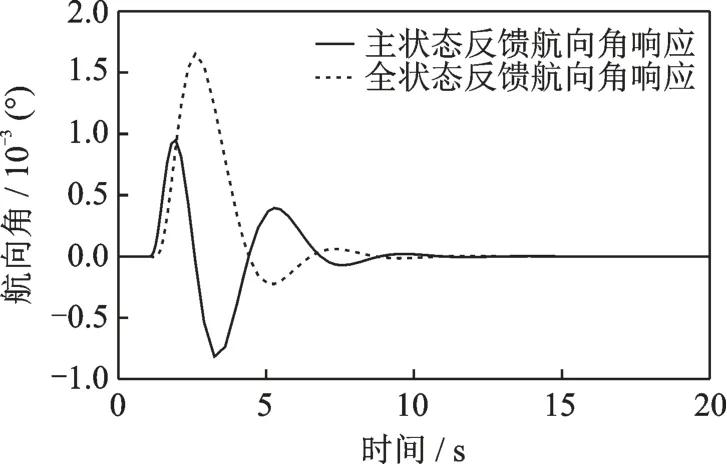
图10 航向角对前飞速度指令的响应Fig.10 Yaw angle response to forward flight speed command
在图中可以看出,本文所设计系统极大抑制了航向角因耦合而发生的改变,在系统应用中更优于全状态反馈系统。
悬停模式下的直升机转弯区别于前飞状态下的协调转弯,航向角变化带给其他通道较小扰动,为验证控制器合理性,给定航向角45°的指令,主通道响应如图11 所示。
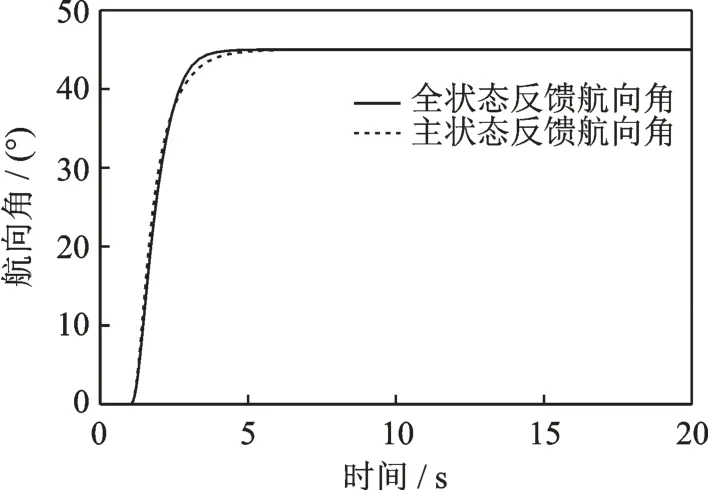
图11 航向角对偏航指令的响应Fig.11 Yaw angle response to yaw command
三轴速度响应如图12 所示。根据图中速度数值大小可知,航向角状态迅速跟随指令变化的同时,其他状态量在控制器的作用下幅值被抑制到很小的值并且快速收敛。主状态反馈控制器的控制效果与全状态反馈形式的闭环系统没有明显的区别,在某些量的控制上面甚至表现得更好。
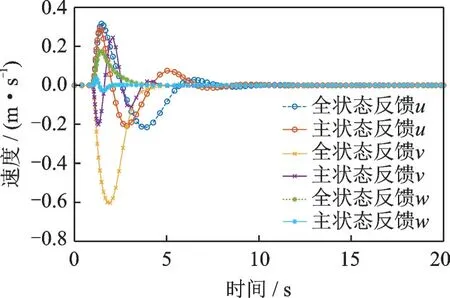
图12 三轴速度对偏航指令的响应Fig.12 Three-axis speed response to yaw command
4 结 论
本文针对直升机飞行控制律设计问题设计了一套改进的LQR 设计方法。通过建立最大化主状态反馈影响因子的指标函数并基于粒子群算法对加权矩阵Q 进行了优化,该设计方法仅需要直升机的数学模型就可以通过优化算法高效得到其对应控制律,解决了现有LQR 设计方法依赖工程经验确定加权矩阵的难题,大大提高了控制律的设计效率。通过对UH-60A 直升机进行飞行控制律的设计和验证结果可以看出,基于本文方法能够得到具有良好控制性能的飞行控制律,采用扩展LQR控制器搭建的仿真模型拥有良好的动态响应与轴间解耦能力,显著提高了直升机的飞行品质,并且在对状态反馈结构进行主动简化的过程中,实时控制效果与全状态反馈相差不大,证明对反馈矩阵的参数优化有很好效果。同时本文得到的控制律阶数不高,易于在工程中进行应用,并且为后期针对特定飞行品质优化的参数调整提供了基础,具有一定的工程实用性。
