直升机切换LPV 鲁棒跟踪控制

张绍杰，李 硕，严 鹏，鲁 可,2

（1.南京航空航天大学自动化学院，南京211106；2.中国直升机设计研究所直升机旋翼动力学重点实验室，景德镇333001）

直升机以旋翼作为主要升力来源，不需要机场跑道，能够很好地实现垂直起降和空中悬停，机动灵活，但比固定翼飞机有更复杂的气动特性，给控制律设计带来了巨大的挑战。线性变参数(Linear variable parameter，LPV)系统具有线性形式，能够描述复杂的非线性模型，进而可采用线性控制理论来解决复杂的飞行控制问题，因此近年来得到了控制理论学者们的广泛关注[1]。在对LPV 系统进行控制器设计时，通常是采用传统的增益调度(Gain scheduled，GS)方法[2]，但这种方法选取调度变量的范围往往决定了系统的性能，如稳定性、H∞性能。若调度变量大范围波动，单一的LPV 控制器不能获得良好的系统性能，甚至导致系统不稳定，所以这种方法难以适用于调参变量大范围时变的非线性飞行控制系统。文献[3]将切换控制和LPV 控制方法相结合，提出了一种参数依赖多Lyapunov 函数的切换线性变参数控制方法。文献[4]根据发动机相似工作原理以及平方和规划，基于发动机全飞行包线的换算线性变参数模型，提出了一种基于区域极点配置的航空发动机全包线切换H∞/LPV 控制方法，通过划分包线来极点配置的方法降低了系统的保守性。文献[5]基于切换系统提出了一种平均驻留时间(Average dwell time，ADT)切换信号设计方法，实现了平均意义上稳定线性子系统间的慢切换。文献[6]基于模态依赖平均驻留时间(Mode-dependent average dwell time，MDADT)方法，研究了一类线性不确定切换系统的稳定性，较ADT 切换信号的设计，MDADT 更灵活、更易实现。

目前国内外有许多学者将重点放在LPV 模型建立上以及ADT 和MDADT 控制问题的研究上。文献[7]结合ADT 方法，将后掠角的变化范围分为3 个区域并分别设计控制器，解决了不同后掠角有不同系统性能的问题，通过切换控制器来保证变体过程中的稳定性。文献[8]对倾转旋翼机纵向模型进行配平线性化，得出在不同短舱倾角不同飞行模式定常飞行时的平衡工作点,采用MDADT 切换鲁棒H∞跟踪控制方法对飞行器从直升机模态转换到固定翼模态的过渡过程进行切换跟踪控制。但目前针对直升机，建立LPV 系统并设计带有MDADT 的切换控制器的研究较少。

本文针对UH-60 军用直升机，以这类直升机的非线性模型为基础，建立LPV 纵向模型，并研究了其纵向模型在MDADT 切换信号下控制器设计方法。 结合参数依赖的多Lyapunov 函数和MDADT 方法，给出了保证切换LPV 系统全局一致指数稳定的充分条件。并考虑由于测量误差和参数飘移等因素而造成的控制器增益变化，设计带有MDADT 限制的切换律。由Simulink 仿真可知所设计的控制律能有效地动态跟踪直升机前飞状态的不同状态量，验证了所建模型和控制算法的有效性和可行性。

1 直升机纵向切换LPV 建模

虽然利用气动力方程组建立的非线性系统能较为精确地描述直升机，但在实际工程中，针对直升机这类高阶、复杂的被控对象，用现有控制理论解决控制问题时仍然存在诸多的限制和局限性[9]。LPV 系统是一类特殊的非线性动态系统，这类系统只有参数是可变的。相比较于传统的线性定常（Linear time invariant，LTI）系统，LPV 系统通过将复杂的飞行器对象进行LPV 建模，可简易描述飞行器动力学方程，从而方便运用鲁棒控制等线性控制理论来设计变增益控制器。

1.1 纵向运动方程的线性化与切换LPV 模型

当直升机作速度大小与方向均不变的定常直线运动时，其处于平衡状态，此时作用于机体轴上的合力以及合力矩均为零，根据牛顿运动定律可以得到6 个平衡态动力学方程。且由于纵向运动模态下不考虑滚转角φ，偏航角ψ，滚转角速度q，偏航角速度r 等的影响，直升机纵向平衡方程为

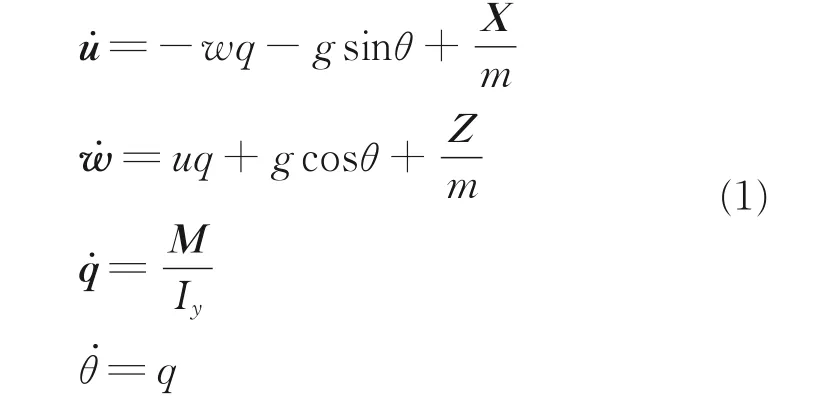
式中：u,w 分别为直升机沿机体轴的线速度；m 为直升机总质量；θ 为俯仰角；q 为俯仰角速率；Iy为直升机惯性矩；X,Z 为直升机在机体轴下各部件气动力的矢量相加；M 为俯仰力矩。

目前常用的将非线性模型表示为LPV 模型的方法有3 种，分别是雅克比线性化方法、状态变换方法和函数替换法。由于雅克比线性化法适用于任何可在平衡点处线性化的非线性系统，本文采用雅克比线性化法来完成模型的建立。

首先需要选择调度变量，并对其作用范围进行划分，由于前飞状态的4 个状态量中，俯仰角速率q可由俯仰角θ 求导表示，因此在选择增益调度变量ρ 时 选 取u,w,θ 作 为 调 度 状 态。且 由 于w 和θ 的数值较小且仅在小范围内变化，因而在整个飞行包线中仅对u 的数值进行划分。

其次需要计算各状态变量的平衡点。方程式(1)可表述为如下形式

式 中：x=[u,w,q,θ ]T，δ=[δe,δc]T，δe为 直 升 机纵向周期变距，δc为旋翼总距。

当式（2）中的f =0 时，便可以得到状态变量和输入变量的平衡点xeq和δeq。对求得的一系列平衡点并进行上述泰勒展开，从而可以得到

通过一系列平衡点并进行上述泰勒展开，从而可得到一系列能局部逼近非线性动态的线性时不变模型，如图1 所示。

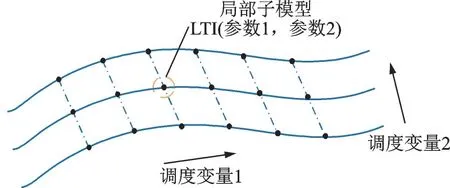
图1 基于雅克比方法的LPV 模型示意图Fig.1 Schematic diagram of LPV model established by Jacobi linearization method

最后将一系列线性化模型进行数值拟合，从而得到直升机LPV 模型

相应于第σ(t)个子区域的LPV 模型表示为

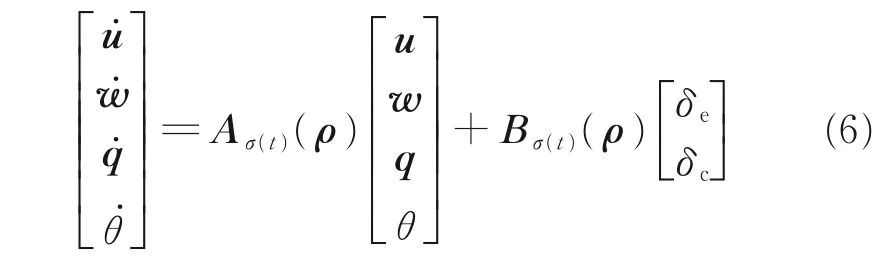
1.2 跟踪控制增广切换LPV 模型

考虑系统式（5）的跟踪控制问题，记指令信号为r(t)，系统的输出y(t) =Cx，C 为适当维数矩阵。则系统控制目标为

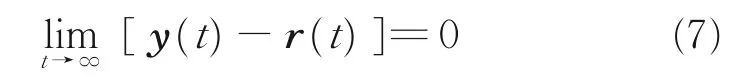
将跟踪误差积分项

2 直升机切换LPV 控制器设计

2.1 LPV 模型的多胞形表示

考虑如下LPV 系统

式中：Hk为已知矩阵，ai为凸分解得到的权系数函数。这种LPV 系统具有凸性质。

若系统矩阵中的A、B、C、D 可由参数{ρ1,ρ2,…,ρn}表示，并具有以下形式

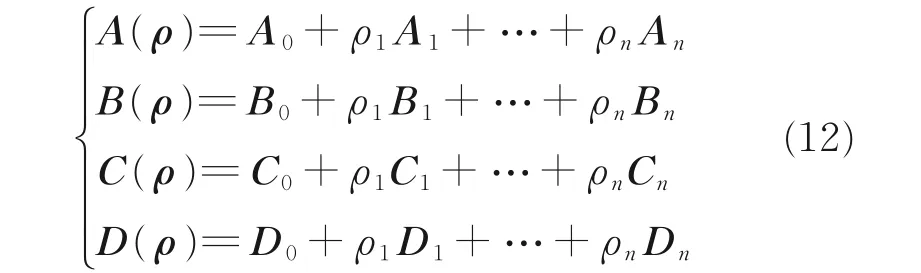
则将这类模型称为参数依赖模型。这类模型可通过调参变量的极值组合转化为多胞形，由此达到简化计算量，减少计算的目的。

2.2 切换LPV 控制器设计

考虑如下切换LPV 系统

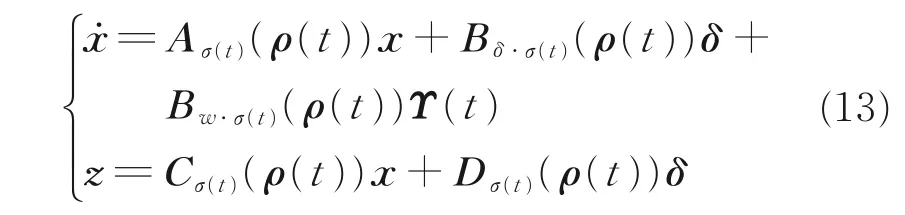
式中：ρ(t)为可时刻检测的变参数，x 为系统的状态变量，Υ(t)为系统所受到的外部扰动。z(t)为H∞性能输出。

定义1[12]对于切换信号σ(t) ∈Λ，假设∀0 ≤t ≤T，Nσs(t,T)表示切换信号在开区间(t,T)间断切换的次数，Ts(t,T )表示第s 个包线区域在(t,T)运行的总时间。如果存在两个常数N0s＞0,τas＞0使得

肖健告诉《中国名牌》记者：“百姓如今的生活水平上去了、经济条件好了，自然会选择更安全、更健康的食物。”

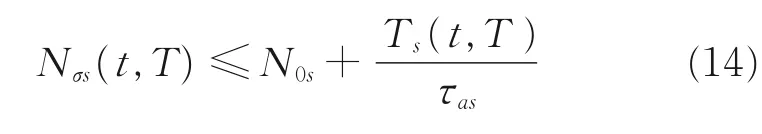
则切换信号σ(t)具有模态依赖时间τas。

定义2[13]假设切换系统满足切换信号σ(t)，存在β ＞0,δ ＞0 满足

切换律σ(t)满足MDADT 限制

则切换系统指数稳定,且满足H∞性能γ。

假设LPV 模型为参数依赖模型，则可对形如式(13)的LPV 切换系统设计状态反馈控制律

来保证系统一致稳定，且具有指定的L2增益γ。

考虑到控制器由于测量误差和参数飘移等因素造成的控制器增益变化，闭环系统可记为

(2)存在常数ε 满足N +εPPT+ε-QTQ ＜0。定理 考虑LPV 系统式(13)，假设系统可用多胞形来表示，则求解H∞控制器的过程可以转变成求解一组LMI，即对每一个包线s 求解一个状态反馈控制器使得闭环系统稳定。给定常数矩阵H，E 和标量γ ＞0，令0 ＜λs＜1，μs＞1，若存在对称正定矩阵Ss＞0，矩阵Usn，有下列LMIs 成立

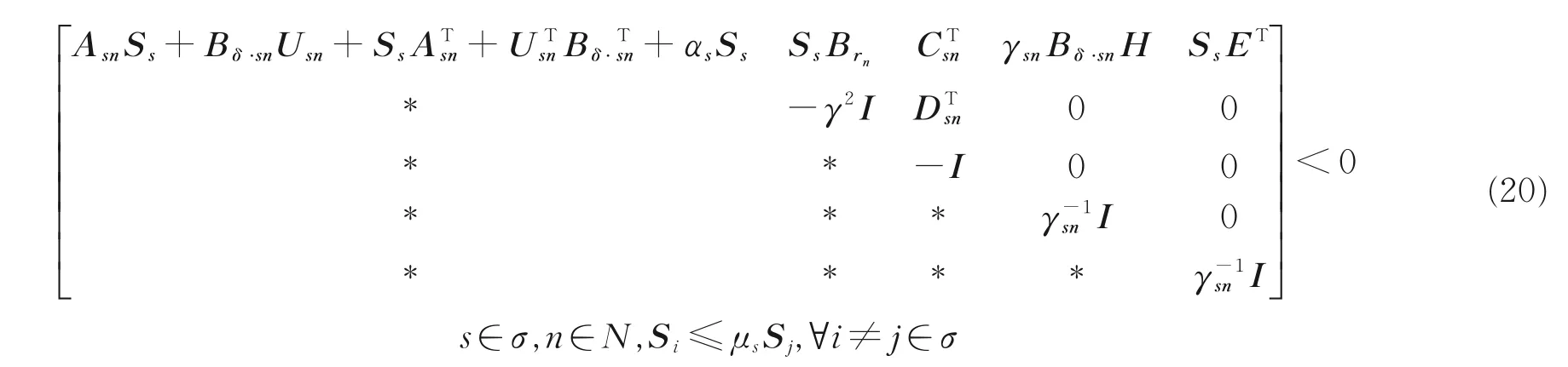
那么在包线范围σ 内存在一组切换控制器

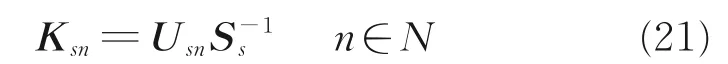
使得切换LPV 系统全局一致指数稳定，并具有L2增益γ，且切换信号满足式(17)。

证明：选取如下形式的Lyapunov 函数

对Vs求导，有

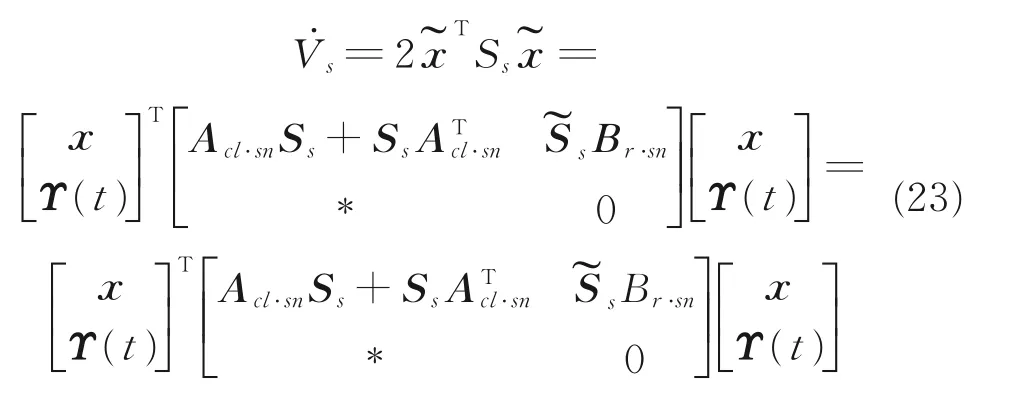
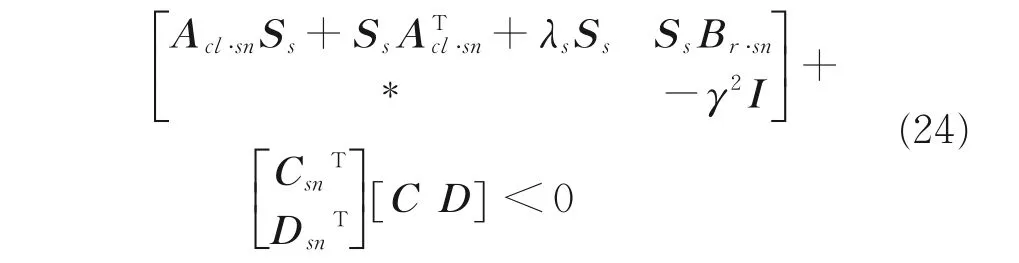
利用Schur 补定理，得到不等式

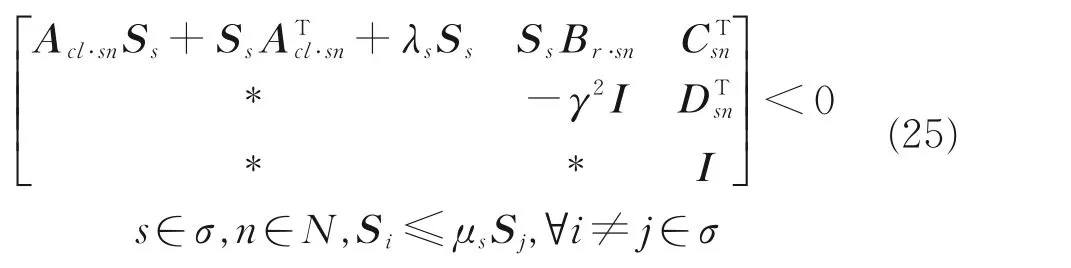
进一步可写成

令KsnSs=Usn，由引理2 可知，存在标量γsn使得

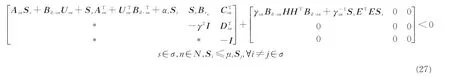
通过Schur 补定理，式(27)等价于

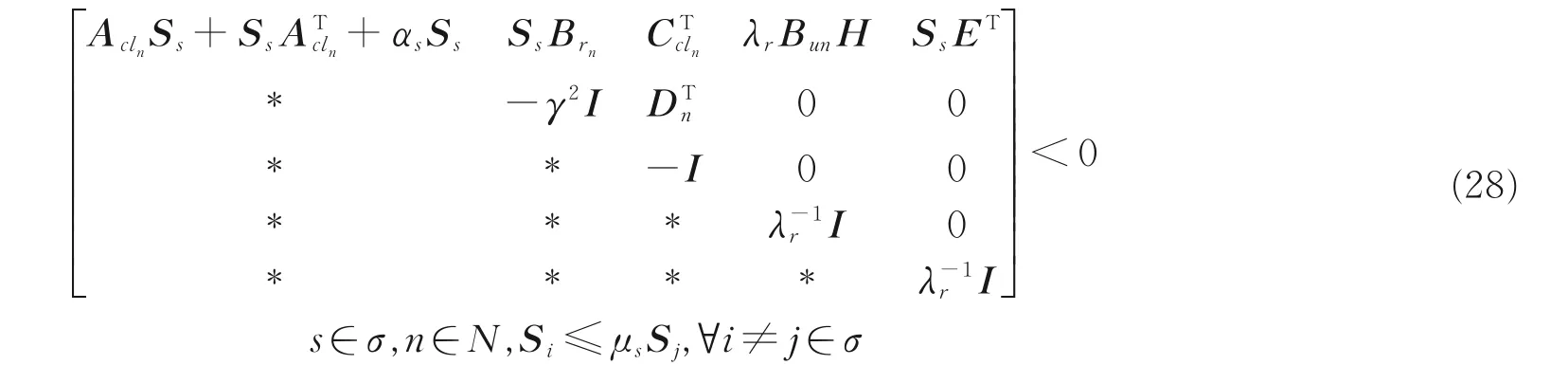
若式(28)有解，那么求得的这一组切换控制器可保证切换LPV 系统全局一致稳定，并具有L2增益γ。证毕。

3 仿真验证与分析

选取机体坐标系下的线速度(m/s)u ∈[0.5,72]，w ∈[-0.03,0.18] 和 俯 仰 角(rad)θ ∈[-0.005,0.102]作为时变参数。将u 划分为3个 区 域：0.5 ≤u ≤20；20 ≤u ≤50；50 ≤u ≤72，从而飞行包线被划分为3 个区域，每个子区域表示为

本文通过选取直升机前飞时平衡点，得到配平模式下的一系列LTI 模型。之后采用多元线性回归对这一系列模型拟合，得到该直升机LPV 模型，再由1.2 节的增广方法对该模型变换，得到仿射参数依赖的模型

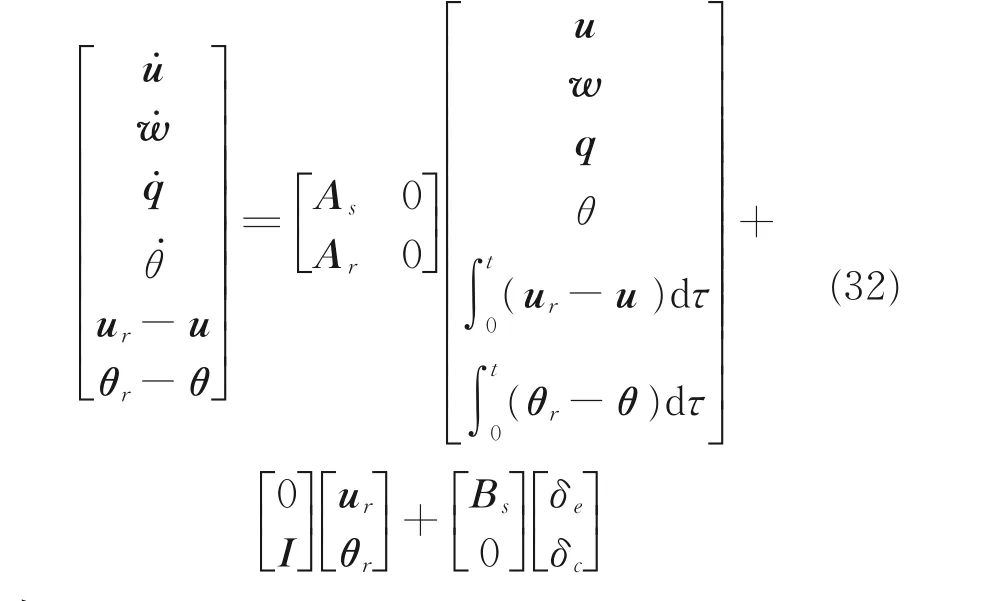
式中

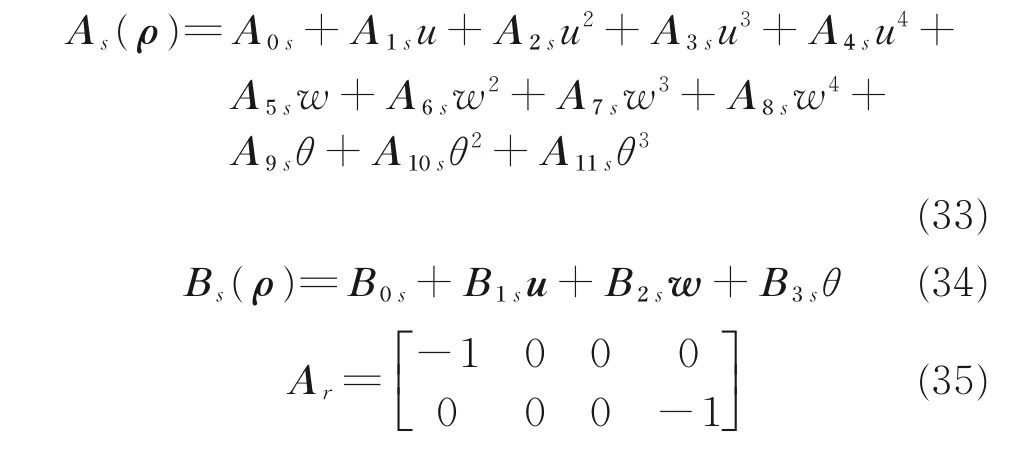
考虑系统的H∞性能输出

u,θ 跟踪曲线如图2～3 所示，w,q 的响应曲线如图4～5 所示。

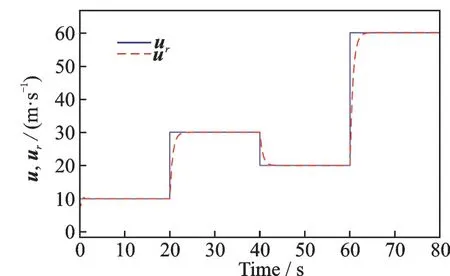
图2 速度分量u 跟踪曲线Fig.2 Tracking curve of velocity component u

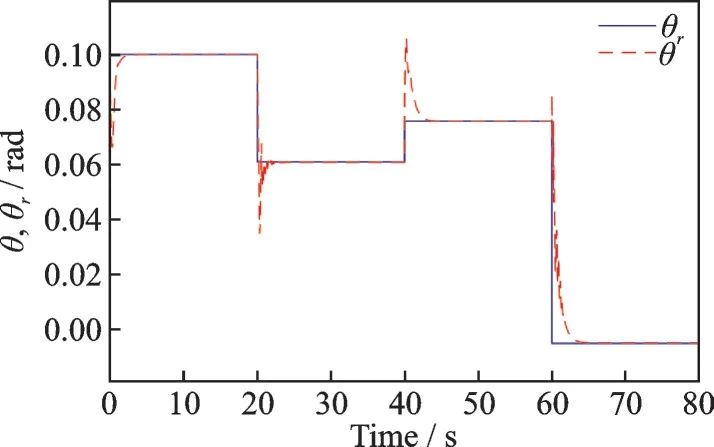
图3 俯仰角θ 跟踪曲线Fig.3 Tracking curve of pitch angle θ

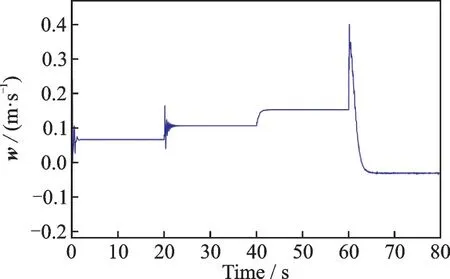
图4 速度分量w 响应曲线Fig.4 Response curve of velocity component w

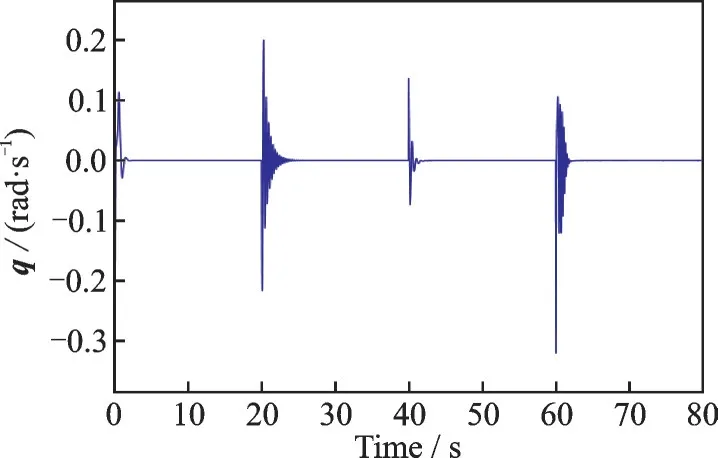
图5 俯仰角速率q 响应曲线Fig.5 Response curve of pitch rate q

切换信号的检测通常需要一定的时间，因此控制器的切换往往滞后于系统模态的切换。但在MDADT 限制下，可忽略其他区域的运行时间，使其小于每个单独区域内任意两个连续切换之间的驻留时间的平均值。由上述仿真结果可知在整个时间域内都能在MDADT 内能有效地动态跟踪直升机前飞状态的不同状态量。

4 结 论

本文针对直升机跟踪控制问题，基于MDADT 切换信号，设计了一组LPV 控制器。对可以表征系统特征的时变参数进行区间划分，结合参数依赖的多Lyapunov 函数，给出了保证切换LPV 系统全局一致指数稳定的充分条件。考虑到控制器由于测量误差和参数飘移等因素而造成的控制器增益变化，通过LMI 求解得到了在MDADT 切换信号限制下的切换律，仿真结果验证了所建模型和控制算法的有效性和可行性。