750 kV超高压扩径覆冰导线的机械振动模态分析

王 芸， 王 宏， 王春耀， 李艳芳， 尚志勇

(1. 新疆工程学院 数理学院，新疆 乌鲁木齐 830011; 2. 新疆大学 机械工程学院，新疆 乌鲁木齐 830047；3. 江西科技师范大学 材料与机电学院，江西 南昌 330013)

在架空输电过程中，导线经常会在强风力作用下发生强烈的振动。通常，如果不考虑攻角变化[1]，根据诱发机械振动的原因和振动的强烈程度，可以把导线机械振动分为3种，即微风振动、次档距振荡和舞动，这3种振动都会给相关的机械元件、电力金具和导线的安全运行带来极大的威胁和严重的后果[2]。导线发生振动的因素有很多，比如风速、导线结构(包括质量)、输电线路的结构等等，但在相同条件下，用有限元分析软件ANSYS判定导线的机械振动形式，主要根据振动频率来进行[3]。在输电工程中，导线发生微分振动的频率是3～100 Hz(有时可以达到300 Hz以上)，次档距振荡的频率是0.5～3 Hz，舞动的频率为0.1～1.0 Hz。

本文中针对LGJK300/50型750 kV超高压扩径覆冰导线进行ANSYS Workbench有限元建模，该有限元模型可以进行网格划分，给后续的模态分析提供基础，同时，模态分析结果可以为输电线路工程运行工况分析提供参考。

1 扩径覆冰导线动力学模型

1.1 扩径导线动力学模型

LGJK300/50型750 kV扩径导线属于钢芯铝绞线[4]，钢芯铝绞线中每层的任何一根单线都是按照一定的绞制角度(捻角)绞合而成的[5]。在实际的机械加工过程中，为了提高产品质量，需要增加绞合的紧密度，节径比越小则环绕得越紧，绞线不容易疏散[6-7]，并且选取节径比的总原则是外层的节径比小于紧邻内层的节径比。参考上述规定，本文中选取的该型号扩径导线的绞制角度和节径比分别如表1、2所示。

表1 LGJK300/50型750 kV超高压扩径导线绞制角度

表2 LGJK300/50型750 kV超高压扩径导线节径比

对于LGJK300/50型扩径导线来说，铝股线和钢股线的直径都是3.07 mm，由于外层铝线和6根钢股线紧密贴合在圆周(建模时各层股线的外径圆，其中，第一层一根钢芯就是辅助圆)上，因此接触方式为螺旋线接触。邻外层和内层铝股线因在圆周上分布的股数少，在层间并不接触，所以该模型中股线间的接触方式为强非线性的点、线接触[8]。后续用ANSYS Workbench进行有限元网格划分[9]时，因为点、线接触而存在一定的难度，所以在建模时，需要通过加大股线尺寸6～10个道(丝)[10]，使得钢股与铝股、铝股与铝股间镶嵌、合并得到理想的动力学模型。根据引入的辅助圆周和各股线参数，得到扩径导线截面与动力学模型如图1所示。

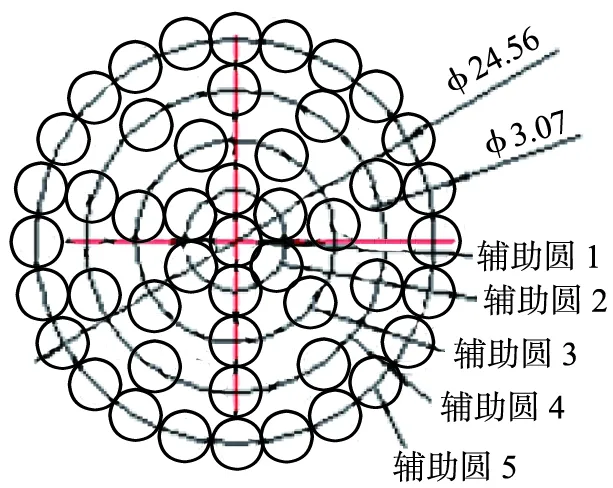
(a)截面

(b)动力学模型图1 LGJK300/50型扩径导线截面与动力学模型

1.2 扩径覆冰导线动力学模型

LGJK300/50型扩径覆冰导线的动力学模型是在上述建立好的非覆冰导线模型的基础上，覆裹一层10 mm厚的覆冰(工程实际中也存在D型覆冰，此处不再赘述)[11]，覆冰的形状近似等同于内径为27.63 mm、厚度为10 mm、外径为47.63 mm的空心圆柱。覆冰与导线外层铝股之间形成有规律的曲面接触，如图2所示。

2 扩径覆冰导线模态分析

2.1 扩径覆冰导线模型网格划分

用UG 10.0建立上述实体模型，之后通过导出Parasolid文件[12]，即x-t格式的文件[13]，用ANSYS Workbench 软件的Browse模块[14]导入模型，读取并赋予单元属性，最终得到LGJK300/50型750 kV超高压扩径覆冰导线的机械动力学模型。采用ANSYS Workbench 15.0软件进行网格划分，需要把全局网格控制中的关联中心(relevance center) 和跨角中心( span angle center)采用中等精度(medium)设置，网格划分结果如图3所示。

图2 LGJK300/50型扩径覆冰导线动力学模型

(a)整段(b)横截面(c)横截面局部放大图3 LGJK300/50型扩经覆冰导线动力学模型的网格划分

从图3中可以看出，机械结构中点、线接触的区域，网格划分较繁杂，覆冰的区域较简单、规则。

2.2 微段扩径导线和扩径覆冰导线机械振动模态仿真比较

2.2.1 非覆冰导线机械振动模态仿真

在试验模态分析的Outline界面[15]上一次性设置好不同阶数机械振动模态(见图4)，有利于机械振动模态阶数和对应机械振型的确定，并且可以很清楚地显示机械振动的模态振型。由于主要分析微段非覆冰导线的模态形式，因此对微段长度的影响并不考虑，只需建立长度为146 mm的微段的动力学模型即可。微段非覆冰导线的每一阶模态对应一种分析云图，如图5所示。

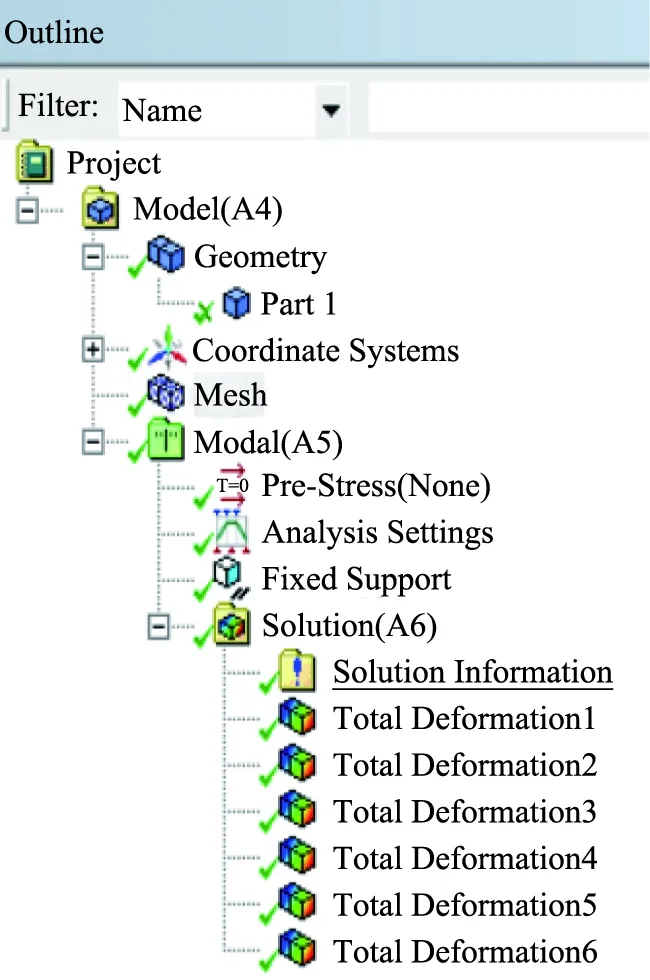
图4 非覆冰导线机械振动模态阶数设定界面

由图可知，非覆冰导线的振型主要是弯扭(扭曲)组合变形。该振动形式会使输电工程中的导线产生移位变形，从而导致跳股或者断线断股的严重后果，因此工程实际中需要采用相应的防振措施来避免移位变形。

2.2.2 覆冰导线机械振动模态仿真

从有利于比较结果的角度考虑，规定微段扩径覆冰导线与非覆冰扩径导线机械振动模态仿真有相同的参考标准[16]。微段 LGJK300/50型扩径覆冰导线的模态分析云图如图6所示。对比图5和图6可知：对于覆冰导线和非覆冰导线2种工况，在单导线静止状态下进行人为激振，设定固定端约束(fixed support)为一个结构实体端面，依据线性定常系统以及机械振动模态叠加原理[17]，覆冰、非覆冰导线呈现的振动形式都是弯扭(扭曲)组合振动。这种振动会使导线产生移位变形，但是，覆冰导线中覆冰的存在在很大程度上保护了导线外围的股线，不容易发生跳股现象，同时，因覆冰而导致导线质量的增加，使得覆冰导线发生舞动的频率更大，其他的次生灾害也会随之而来，应尽量避免。

2.3 不同档距的扩径覆冰导线固有频率

参照LGJK300/50型超高压扩径导线机械振动模态仿真，为了便于得出机械振动模态仿真的结论，需要把扩径覆冰导线长度增大到工程塔杆档距(500 m)的1/10、1/20，并且在无间隔棒[18]的情况下，得到导线长度增加后的模态振型和固有频率。每一阶模态对应一种分析云图，如图7所示。与此同时，得到长段(包括1/10、1/20档距)的振动固有频率，如表3所示。

(a)一阶 (b)二阶

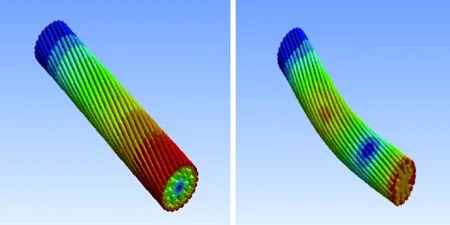
(c)三阶 (d)四阶

(e)五阶 (f)六阶图5 非覆冰导线不同阶数机械振动模态振型分析云图

(a)一阶 (b)二阶

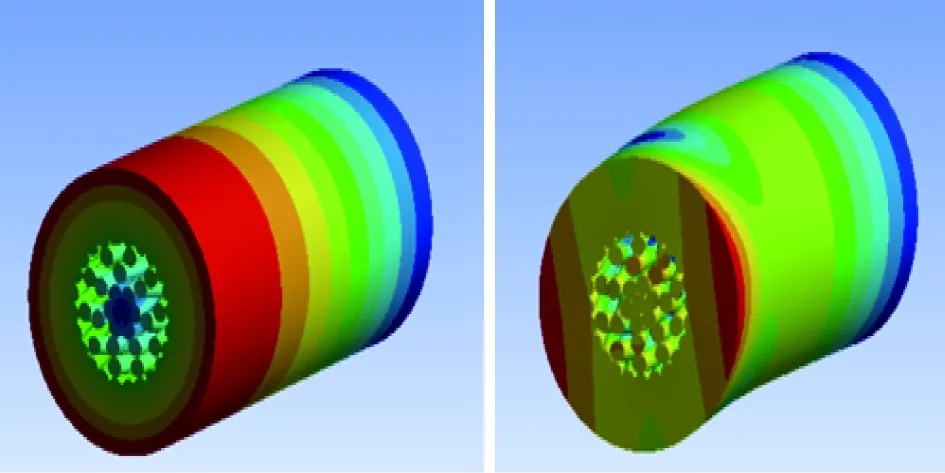
(c)三阶 (d)四阶

(e)五阶 (f)六阶图6 覆冰导线不同阶数机械振动模态振型分析云图

根据图7中各阶模态振型可知，长段的振动形式仍然为弯扭组合(扭曲)振动。从表3中数据可以看出： 1)长段中的1/10档距各阶模态振动频率为0.085 57～0.462 51 Hz，在舞动的振动频率范围之内，振动形式为舞动； 2)长段中1/20档距的一、二阶模态振动频率为0.342 32～0.943 89 Hz，振动形式为舞动，三、四阶模态振动频率为0.943 61～0.943 78 Hz，振动频率既在舞动频率(0.1～1 Hz)范围之内，又在次档距振荡频率(0.5～3 Hz)范围之内，即有舞动频率重合现象，说明振动形式既有舞动，同时也夹杂着次档距振荡； 五、六阶模态振动频率为1.849 80～1.850 10 Hz，导线只发生次档距振荡。

由此可见，在相同工况下，不考虑攻角变化以及流固耦合性对导线振动影响，随着覆冰导线长度的增大，悬垂和振动振幅明显增大，这样会直接导致舞动的临界风速变小，在自然风的作用下，发生舞动的频率增大，次档距振荡的频率减小。若导线长度减小，舞动并非唯一的振动形式，同时也会夹杂次档距振荡，这与工程实践中振动频率的分布相符。至于长度达到何种数值只会产生次档距振荡，还需要进一步研究。

(a)一阶模态(b)二阶模态(c)三阶模态(d)四阶模态(e)五阶模态(f)六阶模态图7 长段导线不同阶数机械振动模态振型分析云图

表3 1/10、 1/20档距长段不同模态的固有频率

3 结论

1)根据线性定常系统以及模态叠加原理，对长度为146 mm的微段和1/10、1/20档距的长段进行机械振动模态仿真可得： 覆冰导线和非覆冰导线的振型都是弯扭组合(扭曲)振动。该振动形式可以使输电工程中的导线产生移位变形，从而导致跳股或者断线断股的严重后果，因此在工程实际中应采用相应的防振措施避免移位变形。对于覆冰导线，因为覆冰在很大程度上保护了导线外围的股线，所以不容易引起跳股现象发生。同时，覆冰量的增加使得覆冰导线发生舞动的频率更大，其他的次生灾害也会随之而来，这方面还需要进一步研究。

2)振动频率与结构模型长度密切相关。对长段进行机械振动模态仿真，结果显示，在相同工况下，不考虑攻角变化以及流固耦合性对导线振动影响，随着覆冰导线长度的增大，悬垂和振动振幅增大，这样会直接导致舞动的临界风速变小，在自然风的作用下，发生舞动的频率增大，次档距振荡的频率减小。若导线长度减小，舞动的同时也会夹杂着次档距振荡。该结论可以为输电线路中的机械结构动态设计及故障诊断提供参考。