基于入侵性杂草优化的机械手逆向运动学求解

杨雨佳， 神显豪， 刘珊珊， 程日光

(1. 广州理工学院 计算机科学与工程学院，广东 广州 510540； 2. 桂林理工大学 广西嵌入式技术与智能系统重点实验室，广西 桂林 541004;3. 华南理工大学 计算机科学与工程学院，广东 广州 510006; 4. 桂林电子科技大学 材料科学与工程学院，广西 桂林 541004)

工业4.0概念的提出意味着智能化时代的到来。为了适应世界制造产业的发展新需求，机器人的应用越来越广泛，同时对机器人的控制复杂度要求也逐步提升，作为机器人控制末端的主要单元机械臂，其视觉伺服控制技术一直是机械工程的一个研究焦点问题[1-3]。

逆运动学求解是机械臂视觉伺服控制过程中的一个重要问题，应用领域也十分广泛，主要分析机械臂末端执行器笛卡儿空间坐标与机械臂关节空间关节变量之间的对应关系[4]。随着工业技术的不断发展，机械臂的结构变得越来越复杂，传统上采用几何算法和代数算法的求运动学逆解方法已经无法在规定的时间和精度范围内完成计算，因此，本文中采用将极限学习机(ELM)和入侵性杂草优化(IWO)相结合的算法来实现快速的六自由度机械臂运动学求解，利用ELM单隐层前馈神经网络相关参数(权值和偏置)随机初始化的优势，以提高求解的时间效率，利用IWO算法提高运动学求逆解的准确度，为改善工业六轴机械臂的视觉伺服控制性能提供支撑。

1 相关研究基础

1.1 问题提出

逆运动学求解主要解决的问题是如何在机械臂末端执行器笛卡儿空间坐标与机械臂关节空间关节变量之间建立对应关系[5-7]。基于几何算法和代数算法的传统求运动学逆解方法已经无法适用于目前大多数高冗余度机器人(几何结构更加复杂)，因此，目前研究人员主要采用神经网络或智能优化算法来解决该类问题[8-11]。例如，文献[8]中提出了基于反向传播(BP)神经网络的六轴并联机器人标定逆运动学求解。文献[9]中提出了基于自适应神经网络的全状态观测器，用于求解逆运动学模型，其创新之处在于将自适应神经网络用于逼近机器人的死区函数和未知模型，使得末端执行器初始位置的误差较小。

类似于上述基于人工神经网络的原理，文献[10]中提出了将模拟退火算法和遗传算法相混合的智能算法来进一步减小末端执行器的误差。文献[11]中通过粒子群优化(PSO)算法来优化BP神经网络的权重参数，以便改善6个旋转自由度仿人机械臂运动学求解性能。

通过比较上述方法发现，现有基于神经网络和智能优化算法的机械臂求逆解仍存在某些问题： 1)多数采用BP神经网络的方法存在收敛速度慢、算法执行效率低的问题； 2)采用PSO或者遗传算法(GA)的智能优化对初始中心的敏感性较大，导致容易陷入局部极小值，全局最优解不准确。这一点在面对具有较多局部最优值的问题时表现十分突出，导致精度不够理想。

1.2 本文研究思路

由于ELM比传统的人工神经网络具有极高的训练速度，因此文献[12]中提出了基于GA-ELM的机械臂振动预测模型，明显提高了实际工作过程中机械臂的工作效率。与此同时，有学者提出了IWO算法并进行了推广应用[13-16]。因为模拟了杂草生物生长方式，所以IWO算法的鲁棒性、适应性较为突出。与PSO和GA等算法相比，IWO算法在处理多峰函数问题时求解能力更佳。黄霞等[13]提出了用IWO算法求解作业车间调度问题，兼顾了全局搜索和局部搜索，实验结果优于PSO算法的。

为了解决以上问题，本文中提出了一种基于入侵性杂草优化的机械臂运动学逆解方法，其创新之处在于： 1)利用ELM输入层权值和隐藏层偏置随机初始化的优势，以保证机械臂求逆解的实时性； 2)利用IWO算法在处理多峰函数问题时求解能力更佳的优势，兼顾全局搜索和局部搜索，以保证机械手求逆解的准确性。

2 六自由度机械臂的正向运动学模型

本文中以六自由度机械臂作为研究对象，并通过最常用的Denavit和Hartenberg提出的为杆件建立坐标系的矩阵方法(简称D-H法)，建立机械臂的正向运动学模型。六自由度机械臂的关节运动约束和模型参数，如表1所示。

表1 六自由度机械臂的关节和模型参数

在机械臂的正向运动学模型中，邻近关节坐标系(坐标系n+1和坐标系n)的变换矩阵为

nTn+1=An+1=

R(z,θn+1)T(0,0,dn+1)T(an+1,0,0)R(x,αn+1)=

(1)

式中：sn+1、cn+1、sαn+1和cαn+1分别代表sinθn+1、cosθn+1、sinαn+1和cosαn+1；R(z,θn+1)、R(x,αn+1)分别为绕x、z轴的旋转变换矩阵；T(an+1, 0, 0)、T(0, 0,dn+1)均为对应的平移变换矩阵。

在六自由度机械臂正向运动学模型中构建邻近关节坐标系的变换矩阵之后，坐标系中机械臂末端执行器位姿0T6为

(2)

式中： [px,py,pz]T为坐标系中末端执行器的空间位置矢量； [nx,ny,nz]T、[ox,oy,oz]T和[ax,ay,az]T分别为坐标系中末端执行器在x、y、z轴上的矢量。

3 ELM-IWO算法

3.1 构建ELM

传统的采用BP神经网络的方法存在收敛速度慢、算法执行效率低的问题，原因是其采用了梯度下降的方式来调节神经网络的权值和偏置，而极限学习机ELM采用单隐层前馈架构，因此学习时间较短，其网络结构如图1所示。

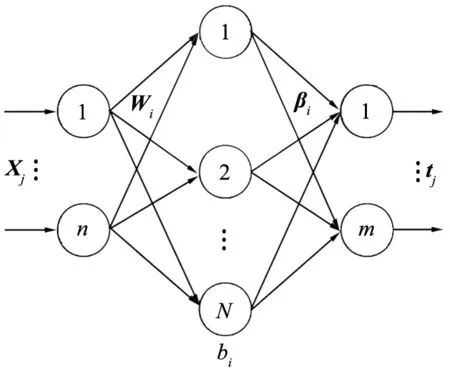
注： bi为第i个隐层节点的偏置； tj为输出矢量； Xj为输入矢量； Wi为输入权值向量； βi为输出权值向量。图1 极限学习机网络结构

ELM的输出函数为

(3)

式中：bi为第i个隐层节点的偏置；oj为输出矢量；Xj为输入矢量；Wi为输入权值向量，Wi=[wi1,wi2, …,win]T；βi为输出权值向量，βi=[βi1,βi2, …,βim]T；h(·)为激活函数。其中，输入权值向量和偏置是随机产生的。

最小化训练误差的方式如下：

(4)

式中：β为输出权值矩阵；T为端执行器值姿矩阵。

利用最小二乘法对式(4)进行求解，获得输出矩阵为

(5)

式中H†表示广义逆矩阵。

通过ELM对六自由度机械臂正向运动学模型求解运动学逆解时，其训练集合为关节角度向量θ=[θ1,θ2, …,θ6]和端执行器位姿T的数据组合(θ,T)。ELM通过训练输出机械臂关节角度向量，完成逆解初解。

3.2 IWO算法原理

生物学上被称为杂草的植物一般会表现出生命力顽强、繁殖能力突出和生长周期短的特性，比农作物具有更强的抗性和环境适应性[13-16]。1962年，MacArthur提出了种群繁殖理论，对种群的繁衍和竞争淘汰策略进行研究。IWO正是一种模拟杂草占地生长与繁殖策略而提出，用来求解约束问题的群智能优化算法，具有以下特点： 1)基于适应度值的繁殖规则； 2)遵循正态分布的种子扩散； 3)采用柔和的竞争排斥机制。

典型的求解问题优化IWO算法分为4个主要操作。

1)种群初始化操作。采用随机原则在求解空间范围内散布m0株杂草，即第一代种子群，其中种子的位置表示约束问题函数的所需解。此外，还需要对全部种子位置的适应度值进行首次评估。

2)杂草的繁殖操作。在杂草种子适应度值排序(从大到小)后执行繁殖操作，如图2所示。

图2 杂草繁殖原理示意图

杂草a在第(h+1)次迭代中遵循的繁殖规则为

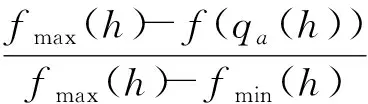
∀a=1,2,…,m(h)，

(6)

式中：qa(h)为第h次迭代后杂草a的当前位置；fmax(h)、fmin(h)分别为第h次迭代后种群的最大和最小适应度；m(h)为第h次迭代后的杂草数量；f(qa(h))为杂草a在当前位置qa(h)下的适应度值； 运算符⎣·」表示向下取整；Smax、Smin分别为杂草能够产生的最大和最小种子数量。

3)种子的空间扩散操作。随着迭代次数的增加，标准差会不断减小，从而确保子代与父代之间的差距。在第(h+1)次迭代中标准差的公式[14]如下:

∀j=1,2,…,D，

(7)

式中：ψ为非线性调制指数，通常取值为2；σmax, j、σmin, j分别为D维解空间中第j维分量的最大和最小标准差；hmax为最大迭代次数。

4)竞争淘汰操作。在上述繁殖和扩散操作后，将父代种群及其后代一起根据适应度值从大到小排序，并开始新的繁殖操作，其他杂草个体均丢弃。

重复迭代以上4个操作，直至达到最大迭代次数 ，此时种群中适应度最大的杂草位置就是寻优过程的输出。

3.3 基于ELM-IWO算法的机械臂逆解

执行IWO的过程中，将机械臂末端执行器的误差最小作为IWO算法的适应度函数，即

(8)

式中：T为ELM计算得到的逆解位姿；T′为输入的目标位姿，T′=(px,py,pz,ox,oy,oz,ax,ay,az,nx,ny,nz)。

基于ELM-IWO的机械臂逆解算法流程见图3。

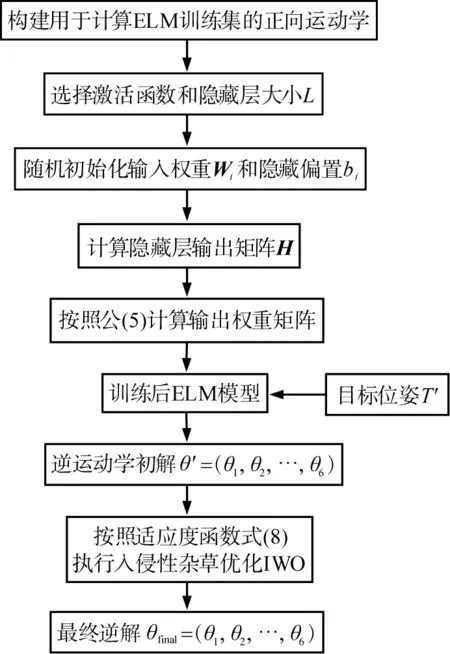
图3 基于极限学习机(ELM)-入侵性杂草优化(IWO)的机械臂逆解步骤

本文中提出的基于ELM-IWO的机械臂逆解算法的主要思路为：首先基于正运动学模型，利用ELM计算出机械臂求逆解的初解，即机械臂末端执行器的位姿θ′=(θ1,θ2,…,θ6)；然后将θ′=(θ1,θ2,…,θ6)作为IWO算法的输入计算机械臂末端执行器的误差，通过迭代进化对种群中各个体进行降序方式排列，选择排序靠前的个体构建新一代的种群，最终将种群中适应度值最小的杂草位置作为所求最小优化问题的最优解。

4 实验结果与分析

为了验证本文中提出的基于ELM-IWO的机械臂逆解算法的性能，在真实六自由度机械臂[17]上分别进行验证分析，并与基于PSO-BP神经网络的求机械臂逆解方法进行综合对比分析。采用的实验数据集共包含7 000个样本，其中随机选择了2 000个样本作为测试样本，其余5 000个样本作为训练样本。ELM-IWO算法中输入节点数量为8，输出节点数量为4，采用的激励函数为Sigmod函数。工业六自由度机械臂为一台UR5六自由度机械臂，如图4所示。

图4 UR5六自由度机械臂

4.1 ELM求机械臂逆解初解的性能

首先对ELM求机械臂逆解初解的能力进行分析。当网络结构中隐藏层节点的数量不断增多时，ELM和BP神经网络的均方差和训练时间对比结果分别如图5所示。从图中可以看出，随着隐藏层节点的增加，ELM和BP神经网络的求机械臂逆解精度均不断提高，两者的精度差距不大。相比之下，ELM的训练时间几乎没有增加，而BP神经网络的训练时间随着节点数量增加而大幅增加。

4.2 IWO优化机械臂逆解的性能

以下对IWO算法优化机械臂逆解的性能进行比较分析。PSO、IWO和混合模拟退火[10]3种优化机械臂逆解方法的末端执行器收敛性能如图6所示，迭代次数均为50次。从图中可以明显看出，相比于其他2种算法，IWO算法达到相同的精度水平所需的时间最少。

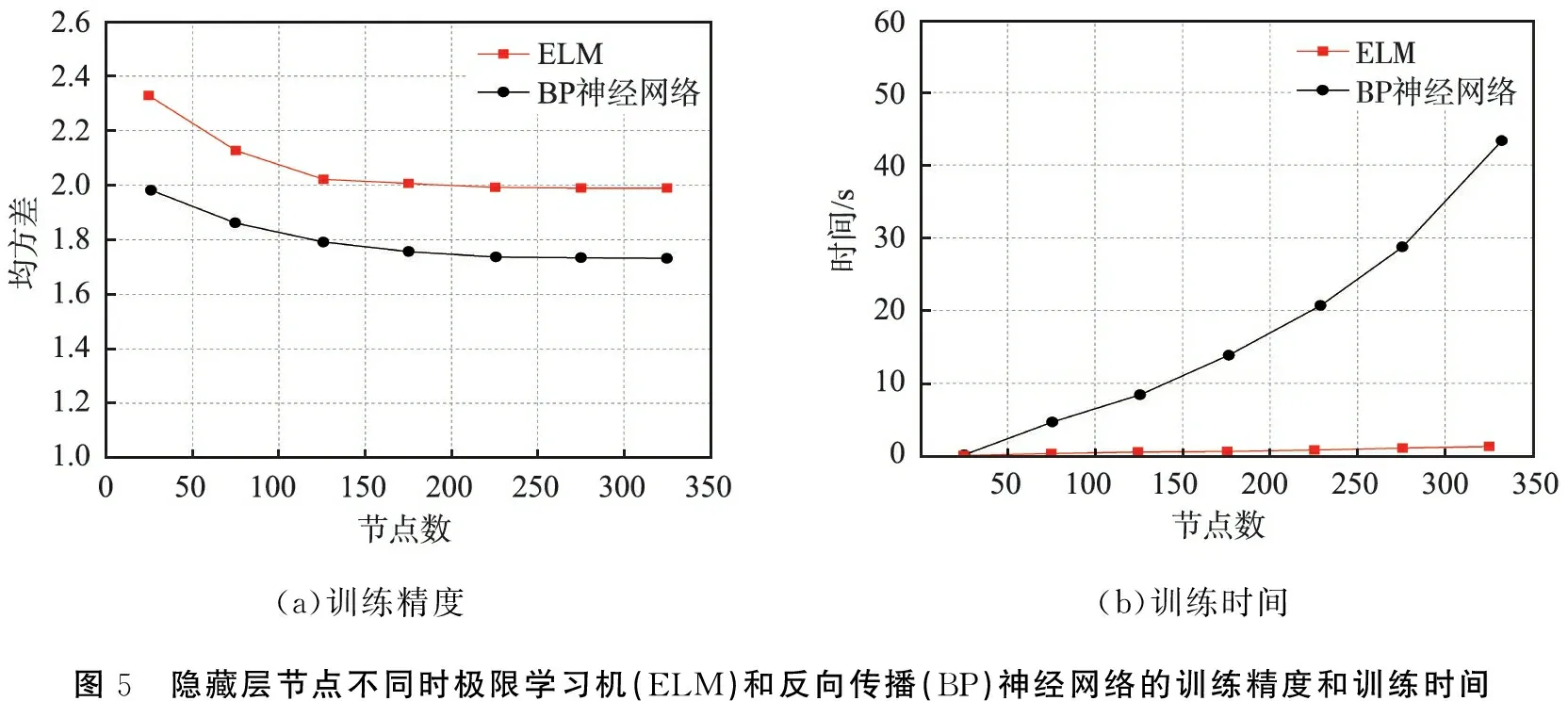
(a)训练精度(b)训练时间图5 隐藏层节点不同时极限学习机(ELM)和反向传播(BP)神经网络的训练精度和训练时间

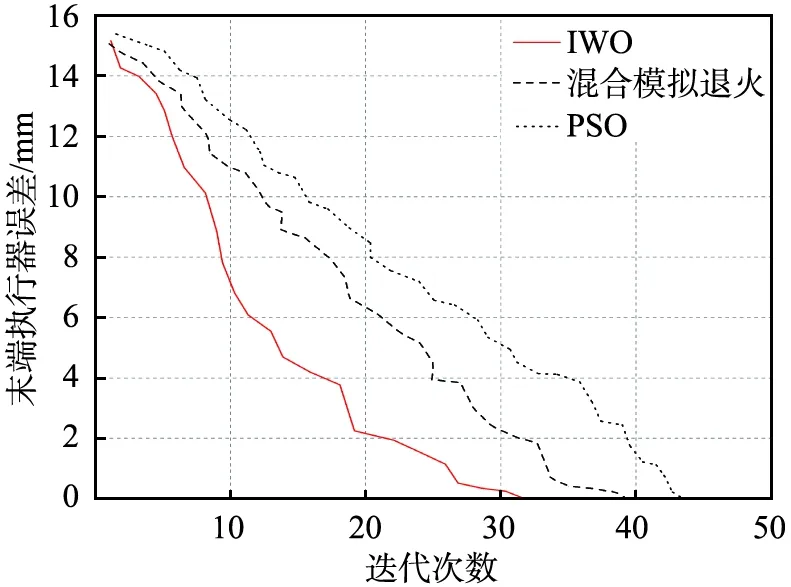
PSO—粒子群优化算法； IWO—入侵性杂草优化算法。图6 不同算法的末端执行器误差

4.3 ELM-IWO求机械臂逆解的结果

对ELM-IWO和PSO-BP神经网络[11]2种算法分别进行了10组目标位姿机械臂对应逆解实验，最终得出2种算法求机械臂逆解的误差和所用时间，结果如图7所示。从图中可以看出，ELM-IWO算法与PSO-BP神经网络算法的误差范围一致，均为1.00～4.00 mm，但是ELM-IWO算法的平均末端误差更小，仅为2.516 mm，据此可以验证该算法具有更高的求机械臂逆解精度。在达到相同精度水平时，ELM-IWO算法具有更短的收敛时间，平均计算时间仅为5.68 ms，实时性更好。

5 结语

本文中将ELM和IWO算法相结合来实现快速、准确的六自由度机械臂运动学求解。首先，利用ELM输入层权值和隐藏层偏置随机初始化的优势，提高了求逆解时间效率；其次，利用IWO算法提高了运动学求逆解的准确度。实验结果验证了ELM-IWO算法在工业六自由度机械臂求逆解上的可行性和先进性； 但是该算法仅在六自由度机械臂上进行了求逆解且为固定位姿，因此后续还需要对其适用性进一步验证，以便在更多的机械臂场景上进行推广和应用。

(a)误差(b)时间图7 极限学习机(ELM)-入侵性杂草优化(IWO)算法与粒子群优化(PSO)-反向传播(BP)神经网络算法求机械臂逆解的结果