光纤波导传光模式及其特性
2021-05-06雷前召董康军张修兴张宁宁吴振森
雷前召, 何 冰, 董康军, 张修兴, 张宁宁, 吴振森
(1. 渭南师范学院 物理与电气工程学院, 陕西 渭南 714099; 2. 西安电子科技大学 物理与光电工程学院, 陕西 西安 710071)
光纤通信的应用已经渗透到社会、生活的各个方面,从传输简单信号到影像快速传递技术,从云主机、云服务器的普及应用到数据安全预警[1]等。新型冠状病毒感染的肺炎(新冠肺炎,novel coronavirus pneumonia,NCP)疫情暴发,更进一步促进了线上购物、线上教育、线上办公以及线上医疗对传统方式的加速替代。随着世界快速进入5G时代,社会的生产、生活方式,企业、国家的组织结构、管理方法、模式都将发生深刻变化。
光纤通信系统容量巨大,优势明显,在引领各国抢占科技领域前沿方面具有巨大潜力。目前常用的二氧化硅光纤在光纤通信中采用的低损耗工作波长为近红外线波长,分别为1.31、1.55、1.62 μm,相比于频率仅为几十兆赫兹的可用通信带宽的短波、微波,光纤通信在这3个低损耗窗口的对应波段各自具有频率分别为17.5、4.3、7.1 THz的带宽储备,如此丰富的带宽资源有力地保障了光纤的大容量通信能力[2]。光纤的特殊材料决定了其具有优良的抗干扰性[3],即使太阳黑子暴发,电离层出现磁暴,光纤通信仍然能稳定、正常运行。此外,当光纤与高压输电线平行架设或与电力导体构成复合光缆时,能够最大程度地提高电力传输线路的运行效率[4]。
波导光学主要研究光在光纤中的产生、耦合、传播和损耗等物理现象和性质[5],以及与之相应的光波导器件,比如光纤耦合器、光纤传感器[6-7]、光纤波分复用器、光开关、光放大器以及光调制器等[8]。集成光路主要研究如何把各种光波导器件集成在同一根光纤中,形成具有一定功能的微型光纤光学系统,以达到纤维集成的目的[9]。上述所有问题都离不开光纤波导的模式传光研究。本文中将光纤波导内矢量场进行简并处理,转化为波导内的线偏振模式,求解柱坐标系下标量场的波动方程,得到线偏振模式的贝塞尔特征方程,并利用线偏振模式的贝塞尔函数解,模拟光纤波导横截面场强分布,分析场强分布特征。
1 光纤波导传光基本原理
光线在光纤中均匀同种介质的纤芯内沿直线传播,在内、外2层介质分界面发生反射和折射。光纤结构及其数值孔径如图1所示,其中,a、b为纤芯、包层的半径,φ为入射光线与光纤轴线的夹角。
入射光线能够通过光纤传输的最大入射角的正弦值定义为光纤的数值孔径rNA,以2φmax为顶角的圆锥体内的光线能通过光纤,根据光纤内纤芯与包层间光线全反射的临界条件,有

a、b—纤芯、包层的半径; φ—入射光线与光纤轴线的夹角。图1 光纤结构及其数值孔径
(1)
式中n1、n2、n0分别为光纤纤芯、包层及包层外介质的折射率。包层外通常为空气,光线在纤芯内多次反射形成折线路径,光线如果与光纤轴线相交,则入射线、反射线、法线、轴线共面,该面称为主截面,其中光线称为子午线,光纤子午线投影图如图2所示。通常,光线入射角φ满足
(2)
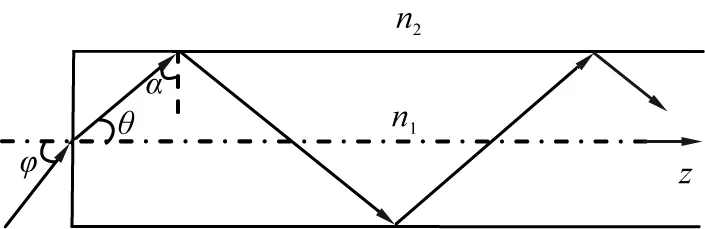
φ、θ—光线通过纤芯横截面进入纤芯的入射角和反射角; α—纤芯内光线在纤芯和包层分界面的入射角; n1、n2—光纤纤芯、包层的折射率;z—空间直角坐标系的竖坐标。图2 光纤子午线投影图
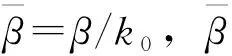
(3)
2 光纤传光标量波导方程及贝塞尔方程解
2.1 光纤传光标量波导方程
光纤波导除了可以传输电场矢量垂直于光线传播方向的横电(transverse electric,TE)波(或H波)、磁场矢量垂直于传播方向的横磁(transverse magnetic,TM)波(或E波)这2种线偏振波,还有传播方向既有磁场分量又有电场分量的HE波或EH波(兼有电场、磁场矢量垂直于光线传播方向),直接求解TE、TM、HE、EH模的矢量精确解很复杂。通常光纤采用弱导光纤(纤芯、包层的折射率满足n1≈n2),在截止频率附近相当宽的频带内,波的传播系数近似相等,极化方向不随z变化,可视为线极化波,问题转化为求解标量方程,则可引用线偏振模式(linearly polarized modes,LP模式)[11]。选用柱面坐标系,使z轴与光纤轴线重合,并且视场分量A满足标量波动方程,则有关系式[12]
(4)
式中:μ、ε分别为介质的磁导率和电容量;r、φ、z、t分别为柱面坐标系的3个分量以及时间因子;A(r,φ,z,t)=R(r)φ(φ)Z(z)T(t)为利用分离变量法所得的解,其中R、φ、Z、T分别为只含有r、φ、z、t的代数因子,φ(φ)=exp(±lφ),l(l=0, 1, …)为围绕z轴旋转的场分量变化的周期数,Z(z)T(t)=exp[j(ωt-βz)],ω为角频率。
将A=R(r)φ(φ)Z(z)T(t)代入式(4),得
(5)
式中:k为波传播的波数;i分别取为1、2。式(5)的解为纤芯和包层中的径向场分量[13],即
(6)
式中:a0、ba为待定系数;V为归一化频率;W为贝塞尔函数的宗量;Jl为纤芯内贝塞尔函数;Kl为包层内贝塞尔函数。
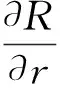
(7)
其中
并且参数β、V、U、W随l、ω、a等的变化而变化。
2.2 标量近似解与传统矢量精确解相对应
根据式(7),当W=0时,特征方程为临界状态,此时V=U,由此确定各模式截止频率。由于U≠0,因此有
Jl-1(U)=0
。
(8)
当l=0时,J-1(U)=J1(U)=0的第1个零点出现在U=0处,传播模式在U=0处截止,该传播模式为LP01; 第2个零点出现在V=3.832处,传播模式为LP02; 第3个零点在7.016处,传播模式为LP03; 第4个零点出现在9.761处,传播模式为LP04。
当l=1时,J0(U)=0的第1、2、3个零点分别出现在U=2.405、5.52、8.654处,对应的模式分别为LP11、LP12、LP13。
当l=2时,J1(U)=0的第1、2、3个零点分别出现在U=3.832、7.016、9.761处,对应的模式分别为LP21、LP22、LP23。
当l=3时,J2(U)=0的第1、2个零点分别出现在U=5.136、8.417处,对应的模式分别为LP31、LP32。
当l=4时,J3(U)=0的第1、2个零点分别出现在U=7.588、8.711处,对应的模式分别为LP41、LP42。
统一使用LPln表示LP模式,其中n为贝赛尔函数的零点数,实际含义为场径向分量变化的半波数[13]。
LPln模式远离截止时,则对应的频率f→∞,k0→∞,则入射角θi→90°,根据特征方程(7),有
Jl(U)=0
。
(9)
式(9)是LPln模式远离截止的传输条件,l取不同值时对应的根值标注于贝塞尔函数曲线,如图3所示。
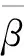
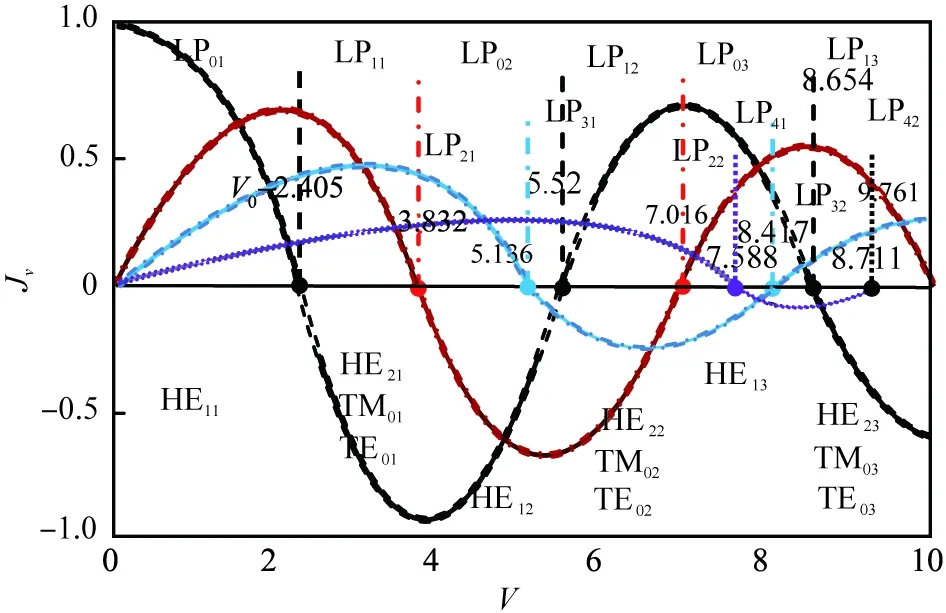
V—归一化频率;Jv—v阶贝塞尔函数;J0—零阶贝塞尔函数,黑线;J1—一阶贝塞尔函数,红线; J2—2阶贝塞尔函数,蓝线; J3—三阶贝塞尔函数,紫线;LP—对应各区间的线偏振模式场,相邻2个根之间为一个区间;TE、TM、HE—矢量精确解,分别对应LP01、LP11、LP02、LP12、LP03、LP13共6个线偏振模式场;LP01—HE11二重简并,此为单模,也称主模;LP11—HE21与TE01、TM01的简并;LP02—HE12的二重简并; LP12—HE22与TE02、TM02的简并;LP03—HE13的二重简并;LP13—HE23与TM03、TE03的简并。图3 贝赛尔曲线中模式的截止与远离截止
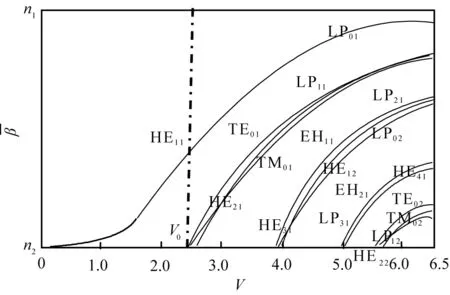
n1、n2—光纤纤芯、包层的折射率;TE、TM、HE、EH—精确场,不同的下标代表不同的模式;LP01—HE11二重简并,此为单模,也称主模;LP11—HE21与TE01、TM01的简并;LP21—EH11、HE31的简并;LP02—HE12的二重简并;LP31—EH21、HE41的简并;LP12—HE22与TE02、TM02的简并。图4 线偏振模式(LP模式)的传播系数与归一化频率V之间的关系
下面分析矢量精确解与标量近似解的关系。
对于弱导光纤,横向分量Hx、Ey、Ex、Hy的振动模式为线偏振,矢量精确解HEl+1,m[Jl(V)]、EHl-1,m[Jl(V)](l=0, 1, …;m=1, 2, …)这2项本征值相同,旋向相反,2项进行简并后,合成线偏振光LPlm模式。
由表5和表6可以看出A、B、C三个影响因素中,影响因素顺序为A>C>B。由表5的均值结果分析,因素A的优劣顺序为3>2>1;因素B的优劣顺序为3>2>1;因素C的优劣顺序为3>1>2。最终选择以A3B3C3为最佳水提工艺条件,即加10倍量水,煎煮3次,每次煎煮1.5 h。
当l=0时,LP0m模式只有二重简并,对应精确解的混合波HElm。
当l>0时,每个LPlm模式有四重简并,径向有2种模式,沿x方向或y方向偏振,由式(6),径向场分量包含角因子φ,角向有cosmφ、sinmφ之分[12]。当l≥2时,LPlm模式由HEi+1,m与EHi-1,m模式简并,而当l=1时,LP1m模式由HE1+1,m与TE0m、TM0m模式简并,简并前、后的对应关系如图3、4所示。
3 纤芯截面LP模式的场强分布模拟及特性分析
根据LP模式的贝塞尔函数解,模拟几个LP低阶模的场强分布。设纤芯的内径为20 μm,光波波长为1.31 μm,纤芯和包层介质折射率分别为n1=1.468,n2=1.458。
LP01模式的场强为
ELP01(x,y)=CJ0(U01r/a)/J0(U01),
(10)
式中:C为常数;U01为纤芯内贝塞尔函数宗量。
由贝塞尔函数解的特性可知,J0(U01r/a)与J0(U01)在取值范围(0,2.405)内均为正值,因此导模的场沿径向无零点。由于l=0,因此导模的场无角向分量。利用式(10)模拟LP01模式场在纤芯截面的场强分布,结果如图5(a)所示。从图中可以看出,光以纤芯轴心为中心分布,越靠近轴心时场强越大。
LP02模式的场强为
ELP02(x,y)=CJ0(U02r/a)/J0(U02), 3.823<
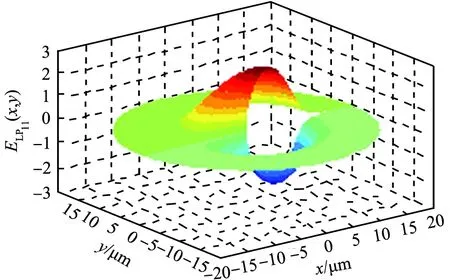
U02<5.520, 0 (11) 式中U02为纤芯内贝塞尔函数宗量。 由贝塞尔函数解特性可知, 在宗量取值范围内,J0(U02r/a)有零点r=2.405a/U02,在该零点两侧值变号,而分母J0(U02)不变号。由于l=0,因此导模的场无角向分量,纤芯截面LP02模式的场强分布模拟结果如图5(b)所示。由图可知,纤芯中心为一个亮斑; 以纤芯轴心为中心分布一个亮圆环,以r=2.405a/U02环线为界,两侧场强变号。 LP11模式的场强为 ELP11(x,y)=C[J1(U11r/a)/J1(U11)]cosφ, 2.405< U11<3.823, 0 (12) (a)LP01模 (b)LP02模 (c)LP11模 J1(U11r/a)与J1(U11)在其宗量范围内均为正,角因子φ有零点π/2、3π/2,这2个角的边线对称且构成连线,称为零线,零线两侧场强符号相反,模拟结果如图5(c)所示。 LP21模式的场强为 ELP21(x,y)=C[J2(U21r/a)/J2(U21)]cos 2φ, 3.823< U21<5.136, 0 (13) J2(U21r/a)与J2(U21)在其宗量范围内均为正,角因子φ有零点π/4、3π/4、5π/4和7π/4,且两两构成对称对角线,为2条零线,零线两侧场强符号相反,模拟结果如图5(d)所示。 通过几种低阶模的模拟及其结果分析可知,与利用模式的截止、远离截止进行的分析相比,两者得出的结果一致,但是横截面场强分布模拟更形象地显示了各模式场强分布特点。 本文中通过对光纤纤芯轴线横截面的场强分布进行模拟,并分析模拟结果,得到以下结论及启示: 1)当归一化频率V小于2.405时,光纤只有主模LP01,即为单模传输,模拟结果显示,光线集中在光纤内芯中心部分。单模光纤能够完全避免模间色散,可以进行大容量、长距离传输。 2)当V大于2.405时,光纤内的传输方式为多模传输,会受到色散影响,将无法实现大容量、远距离传输。 3)在设计制造光纤时,应通盘考虑纤芯折射率、半径、相对折射率差以及光频率参数,使结构参量满足单模传输条件,保证光纤中只有LP01模式传输。 4)本文中主要研究阶跃光纤传播模式,在实际应用中还有渐变光纤,阶跃光纤是基础。如果选择渐变光纤的折射率按双曲正割规律分布,能实现完善的子午线自聚焦效果,从而有效地消除模式色散的影响。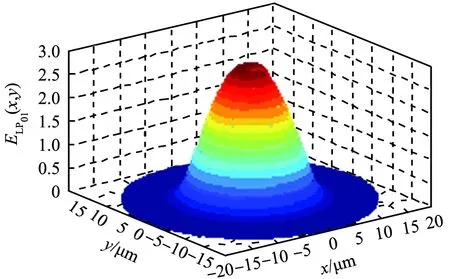

4 结语
