论数学解题教学的教学

陆 珺，胡晴颖

论数学解题教学的教学

陆 珺1，胡晴颖2

（1．苏州大学 数学科学学院，江苏 苏州 215006；2．长兴县泗安镇中心小学，浙江 湖州 313113）

数学解题教学的主要任务是教学生学习解题．数学解题教学的教学，主要任务是教职前数学教师学习如何教学生学习解题．职前数学教师在解题教学的学习中，面临从会“解”到会教“解”的知能跃升和从会教“解”到会教“学解”的知能完善的两重困境．数学解题教学的教学，可通过传授启发性提示语，开展示范教学和采用线索式板书等策略化解困境．

解题教学；教“学解”；启发性提示语；示范教学；线索式板书

1 问题提出

解题是数学活动的基本形式和主要内容，也是其自身的存在目的和兴奋中心[1]．数学学习离不开解题学习，故数学教学离不开解题教学．涂荣豹教授认为，在数学解题学习中，学生的主要任务并不是解题，而是学习解题，因此教师教的重点和学生学的重点，不在于“解”而在于“学解”．以“解”作为出发点，注重的是解题的结果；以“学解”作为出发点，注重的则是解题的过程[2]．照此，数学解题教学的主要任务不在于教“解”而在于教“学解”．那么，数学解题教学的教学，其主要任务就不在于教（如何）“教‘解’”而在于教（如何）“教‘学解’”．尽管这样阐述不免有文字游戏的嫌疑，但从学生的解题学习关联至教师的解题教学，再上溯到数学教师教育中解题教学的教学，个中逻辑是明白无误的．3者各自的主要任务与其习惯性地被误作主要任务的非主要任务的对照和阐释见表1．

表1 “解题学习”“解题教学”“解题教学的教学”之 主要任务与非主要任务

2 教“学解”之研究概况

数学解题教学的研究可谓硕果累累，尤其是广大一线教师为其倾注了宝贵的经验与智慧，但聚焦于教“学解”这一主要任务的研究尚不多见．文[2]认为“学解”最有效的方法是“在解题中学习解题”，即在尽可能不提供现成结论的前提下，亲身独立地进行数学解题活动，从中学习解题，学会“数学地思维”，哪怕解题最终没有到底，也会有所发现，有所体验；文[3]认为重视各种具体的解法技巧，轻视普遍的解题思维方法是数学解题教学的一大误区，指出解题教学要充分暴露解题思维过程，显示为什么要这样做和怎么做的思维过程，突出解题中的探索环节及解题方法被发现的过程，以培养学生解题思维中的调控能力；文[4]认为数学解题过程包含具体的认知过程和更高层次的元认知过程，学生解题能力的差异实质在于学生元认知水平的差异，并借助例题分析阐明加强元认知的培养与训练是提高数学思维能力和解题水平的“超越”手段，是波利亚解题思想的延伸和发展．上述研究集中在2000年左右，如果要从其论点中提取关键词，大概非“（解题）思维”和“元认知”莫属，而这两个词语的结合，不难使人转而关注波利亚的启发性提示语．

文[5]认为在解题教学中，教师为学生所能做的最大好事是通过比较自然的帮助，特别应当反复经常地使用波利亚的提示语，促使学生自己想出一个好念头．而这些提示语，部分是针对问题具体内容的，也就是“客体水平”的，属于认知性的；还有部分是以解题者自身为对象，针对主体内部心理抽象认识过程的，属于元认知性的．研究者认为对于元认知性的提示语的经常自觉地运用，是提高解题元认知能力的有效途径．为此，在文[6]中提出了两套着重帮助学生理解题意的元认知提示语．一是如何着手解题，即当遇到一个陌生的新问题时，最先开始时应该如何思考；二是如何理解题意，包括解题者能用自己的语言重述问题的表层理解和把问题的每一陈述综合成条件、目标统一的心理表征的深层理解．这两项研究产生于2002—2006年间．

此后十余年，出现了若干着重于启发性提示语的应用研究．如文[7]提出教师应提炼具有层级的元认知提示语用以克服数学启发式教学中的偏差现象，并以“正切函数的图像和性质”为例简单列举了元认知提示语的设计；文[8]梳理了启发性提示语的起源与发展，并就“任意角的三角函数”示范了其在不同教学阶段的应用；文[9]探索了启发性提示语在解题中的应用，认为其转换的问题，不是简单的文字浏览和在思想上的一掠而过，而是对每一个对象的意义、性质、不同对象的关系的深入思考与探究，特别是能否转化为其它的意义与关系，同时指出这种贯穿于所有问题之中的思考是数学解题最基本的思考方法，当然不是万能的方法；文[10]通过课堂观察和记录稿分析，发现专家型教师较熟手教师善于运用元认知提示语使学生经历“思维和情感”的困惑，注重思维过程和思维策略的引导；文[11]呈现了将元认知提示语运用于初中数学解题的一则案例．

从学界目前的研究来看，第一，关于教“学解”的研究甚少，远没形成气候．究其原因，大概是受应试教育的功利驱动，研究目光基本投注在解题教学的一般方法与策略上，鲜有人能深刻认识解题教学的意义并为其从长计议；第二，波利亚的启发性提示语之于解题教学的研究，已有较为权威的理论阐述和少量的实践探索；第三，解题教学的教学研究处于无人问津的状态，即缺乏对数学教师的解题教学知能该如何养成这一问题的思考．该研究若不予启动，对解题教学的研究恐怕多半是徒劳．譬如就教“学解”而言，教师在践行解题教学主要“教什么”之前，总得先认同“为什么”且掌握“怎么教”，这是职前数学教师教育应有的担当，不能一味期望由在职培训来完成教学信念重塑与行为纠偏．

3 解题教学之学习困境

数学课课型不外乎新授课、习题课和复习课，几乎没有一堂数学课可以跟解题撇清关系，并且“中学数学教学首要的任务就是加强解题的训练”[12]，因此，数学解题教学知能是职前数学教师的一项必修基本功．然而，因长久以来包括数学教师发展者在内的众人的认识误区与疏漏，其学习过程中存在两大困境．

3.1 会“解”≠会教“解”

“解”是以自我为中心的个体活动，教“解”则是以学生为主体的师生互动．会“解”是针对数学问题，按照自身的知识和能力水平去处理信息，求得解题思路与方法；会教“解”是针对数学问题与学生情况，按照学生的知识和能力水平去处理信息，实现学生对题意的理解，对解题方法的消化和对解答过程的掌握．两者绝然不能等同．职前数学教师在经过4年数学专业学习后，兴许能轻松胜任大部分初等数学题的求解，但要将内隐的解题知能外化为教学语言却非易事．若没有专门的训练，便只能靠个人摸索和模仿，而最终表现如何还得看悟性程度．另外，职前数学教师所拥有的作为学习者的经验不容小觑，丰富、强大的经验系统易导致其教学初期的表现成为他人教学的影射，即“用他们以前被教的方式进行教学”[13]．如此，一些有失偏颇的教学方式可能得以沿袭，譬如用告诉、呈现代替了启发、引导．因而，数学教学论教师及时有效的专业指导的介入，对于职前数学教师实现从会“解”到会教“解”的知能跃升无疑是必要的．

3.2 会教“解”≠会教“学解”

数学解题活动，作为一种数学的思维活动，是个体头脑中数量丰富、生动活泼的元认知活动的短时积聚．但凡经精心编制，能给学习者造成一定困难的数学题，成功求解的背后，总有解题者的“该从哪里突破”“问题的条件足够了吗”“所有条件都考虑进去了吗”等大量对自我思维趋向的提示，其不仅预测、调节、监控解题活动的进程，更直接作用于解题思路的生成．寻找解题思路正是解题活动最重要又最困难的环节．缺乏该环节的解题教学止步于教“解”，即满足求解过程的讲解，互动中只需指向具体信息加工的认知性提示语．而教“学解”则意在解题思维的训练，另需上述自我诘问式的元认知提示语的参与．只会教“解”的教师，教给学生的是在模仿中解题，是“鱼”“渔”之成分；而会教“学解”的教师，教给学生的是在解题中创造，是带有个人创见的“渔识”．从会教“解”到会教“学解”的知能完善过程将是颇费心力的攀登，因为这不仅需要扎实的数学功底和熟练的解题技能，更要深谙学生的认知特点，尤其是清楚其思维走向中的坡道、坦途和可能的弯路、岔路．

4 解题教学的教学之应对策略

从日常课堂教学行为中析出的导入、提问、结束、语言、板书等属于微观知能，而由教学内容所区分的概念（命题）教学、解题教学、思想方法的教学等属于中观知能，其实践需要综合运用各项微观知能，同时又是学习备课、说课等宏观知能的基础．所以，在职前数学教师教育中，解题教学的教学本身是一项承上启下的核心任务．以下3项策略可用以应对解题教学的学习困境．

4.1 传授启发性提示语

现实教学中，多数教师对“如何寻找解题思路”要么避而不谈，要么讲解不清，其根源基本在于启发性提示语的缺位．波利亚的启发性提示语包含认知提示语和元认知提示语．前者聚焦具体策略和方法，不同于简单机械、无关痛痒，甚至冗长耗时的一般性提问，它指向清晰、逻辑连贯，能有效触发思维锚点，展示思维过程，暴露思维盲点；后者超越具体对象而具有普适性，符合学生思维特征和问题解决规律，从而获得诱导出正确念头的可能，有助于推动思维进程，更利于形成一种思维习惯，在潜移默化中使学生学到比任何具体数学知识更重要的东西．两者共同作用于认知目标的达成和解题思维的训练．善用的前提是会用，那么解题教学的教学就要为此提供机会．数学教学论教师可基于波利亚解题理论的教学，在解题教学的讲解与示范中突出呈现相关的启发性提示语，并布置必要的解题教学练习用以强化职前数学教师对启发性提示语的捕捉、整理与表达．

4.2 开展示范教学

说一千道一万，不如做示范．示范教学是教师有目的地以示范技能作为有效刺激，充分调动学生的视觉和听觉，形成表象及联系，使其在观察、思维、模仿、操作中领悟理论精髓，掌握技能要领．教师知识与专业发展的特点决定了示范教学方法尤其适用于教师教育技能的初期学习．因此在解题教学的教学中，教师与其向学生反复说道如何运用启发性提示语，如何提问、等待、回应，如何设计课件和进行板演等，不如在理念传达之后选用合适材料，亲自上阵或邀请专人现场演绎，通过技能的真人化动态演示，带给学习者生动直观的认识，从而弥补空洞说教之不足．

4.3 采用线索式板书

随着现代教育技术的日益普及和频繁更新，“零板书”现象在高校课堂中已比比皆是，尤其是很多文科课程的教学，其精彩纷呈的课件与干净无痕的黑板形成了鲜明的对比．殊不知，教师在“快速电子小黑板”的播放中，忽视了对教学内容的全景式呈现与教学思维的精细化剖析，而学生，常在麻木呆滞的观看中被打乱思维节奏，放弃了积极思考．事实上，现场性与生成性的融合使得板书具有课件所无可比拟的优势，尤其是通过串接知识主干以展现教学内容的逻辑顺序或相互关系的线索式板书，能够将复杂过程化繁为简，便于理解与识记[14–19]．所以无论是中小学数学课堂的解题教学，还是数学教学论课堂对解题教学的示范，都可以构思线索式板书，在呼应教学语言和课件的同时，让学生的思维跟随教师的现场板演而活动得通透明白．

5 解题教学的教学之课例呈现

下文呈现一则数学解题教学的教学课例．限于篇幅，对课例内容择要阐释．

5.1 内容与课时安排

教学的内容与课时安排见表2．这里有两方面考虑．第一，解题是有逻辑的，解题教学要循逻辑而教．对于解题教学的教学，亦应使内容编排符合最易为学生所接受的逻辑．对数学解题学习的认识是理论教学的重点，启发性提示语的教学既为重点又为难点，因此理论课时的第1课时在内容重要性上高出一筹．进入第2课时，教学内容的理论段位和实践难度逐次降低，学生的成就感将随学习进程得到增强．第二，学科教育学教学中，一味灌输教育理论或片面追求技能训练均是极端的做法，理论教学和实践训练须置于同等地位，相互穿插，确保理论有实践的生动反馈，实践有理论的有效支撑．考虑到小组规模与模拟教学后的多元评价的开展，安排2课时的实践教学最为适宜．

表2 内容与课时安排

5.2 教学过程

第1个理论课时的教学过程见表3．5个教学阶段由生疑释疑，求知再生疑，再求知再释疑构成的多个教学环节所串接．教学阶段的区分以师生行为为依据，教学内容的序号表示内容性质的分类，两者不作严格对应．表3只呈现教学内容的梗概，但清晰刻画每一个教学环节的“教”与“学”，这是以“教与学对应的原理”作为教学研究方法论思想的体现．两处教学结束（教学环节五、七）中，给予学生充分思考和讨论的总结方式体现了教学的主体性原则．课末，提供分别聚焦于数（式）、形推导的高、初中习题各一道，供学生按个人的思维偏向和从教意愿等进行选择练习．事实上，既为学生把关练习材料的质量，又给予其一定的自主选择权，这应是教师在布置学习任务中一以贯之的做法．

表3 教学过程（第1个理论课时）

5.3 示范教学

5.3.1 教师的示范教学

例1是教师进行示范教学的例题，其对应的启发性提示语的设计文本见表4．以该三角函数综合题为载体进行启发性提示语应用的第一次示范教学是合适的．首先，应用伊始的问题串以偏短为宜，所以构成求解第一问的4组提示语数量适当．其次，求解第二问需要的提示语数量加倍，这是新知运用中一个必要的爬坡，并且此时学生以准教师的身份进行教学观摩，师生双方将以比较平等的姿态共同讨论确定所有的提问、分析与解答，因而不必有过多难度方面的担忧．第三，该题的解题回顾是比较容易进行的，如文本中的两问便是多数解题者的想法．

（1）求+的值；

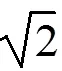
表4 启发性提示语的设计文本（1）

5.3.2 实习教师的示范教学

例2是用于第二次示范教学的具备中考题难度的综合几何题，其对应的启发性提示语的设计文本见表5．因为是第二次应用，问题串可适当变长，但又需考虑此时由实习教师（同专业大四学生）扮演初中数学教师，参与课堂的学生扮演初中学生，所有的提问、分析与解答都将在双方的角色扮演中一气呵成地获得，所以问题串又不宜过长．于是，分别由5组、7组提示语构成的两个问题串，首先符合了数量要求．再者，该示范属于拟实验教学，其顺利与否在很大程度上由“师生”双方的互动有效性所决定，因此对每一问的提问方式作了细致考虑．另外，从例1到例2，从函数转向几何，从高中数学变为初中数学，学生的角色由准教师切换为初中生，其“学”的任务由观摩、讨论调整为观摩、合作，仿若数学的变式教学般作了多重“变式”，目的是确保学生对启发性提示语的确切掌握．

如果说第一次示范教学能够掀起课堂教学的一个小高潮，那么第二次示范教学将当之无愧地成为课堂教学的高潮，学生的课堂参与度和思维兴奋度都将在此时段到达巅峰．因为第一次示范教学，除了示范还包含一定比例的讲解，属于为解释或强调而作的旁白．但是第二次示范教学，则是实习教师的一场专注、倾情的现场“演出”，是一次纯粹且流畅的示范．并且因为和主演身处同一时空场域，学生个个能够亲身参演与现场观演，这一“课中课”的形式将使他们获得远胜于通过阅读教学文本或观看教学视频而得的感受．此外，受邀“演出”的实习教师是在全国或省级师范生教学技能竞赛中获奖的同专业大四学生，不仅知识基础扎实，教学技能过硬，“演出”前还需在教师指导下打磨讲稿，试讲数次，所以作为在专业内小有名气的优秀学长和胸有成竹跃跃欲试的新手教师，其所奉献的这场课堂“真人秀”无疑将是关于榜样效能的一次完美彰显．

例2 在△中，∠=45°，∠=60°，=2，点为延长线上的一点，且∠=∠，⊙为△的外接圆．

（1）求的长；

（2）求⊙的半径．

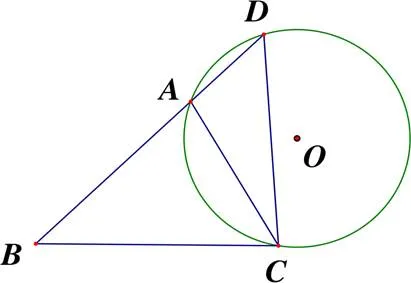
5.4 课件与板书设计

启发性提示语外化于教学行为的鲜明特征是用带有启发性的教学语言有序激发学习者的解题思维．以例1第一问的教学示范为例，图1左图的4个文本框将跟随师生互动逐个呈现，同时伴随分析、解答的过程，教师用数学符号与公式进行简单板书（图2）．于是，配合着图1左图动画的依次播放，教师同步完成板书（1）~（11）（序号表示板演顺序）．接着，在回顾图1左图和板书（1）~（11）中讲解、板书（12）、（13），顿时令学生感悟启发性提示语之于解题的作用．随后，课件切换至图1右图，一幅“自顶部”缓缓展开的流程图将“启发性提示语的设计有哪些原则”的疑问自然抛出，充分讨论之后，教师水到渠成地归纳、板书（14）~（17），末尾以图1右图中一个动画的播放强调核心原则：由远及近，成为这一阶段教学的点睛之笔．

如格言“I hear, I forgot; I see, I remember”所言，精心设计的启发性提示语若只从听觉通道进入学习者大脑，刺激力度是微弱的，但配合使用课件、板书等视觉呈现方式，经由视、听觉碰撞而获得的将是1+1＞2的效果．当然，多种刺激的编排方式需用心研究．实际上，语言的听觉传递与课件、板书的视觉呈现是教学的两条明线，而学习者的解题思维活动是一条暗线，明线应为牵引暗线而设计、运作．

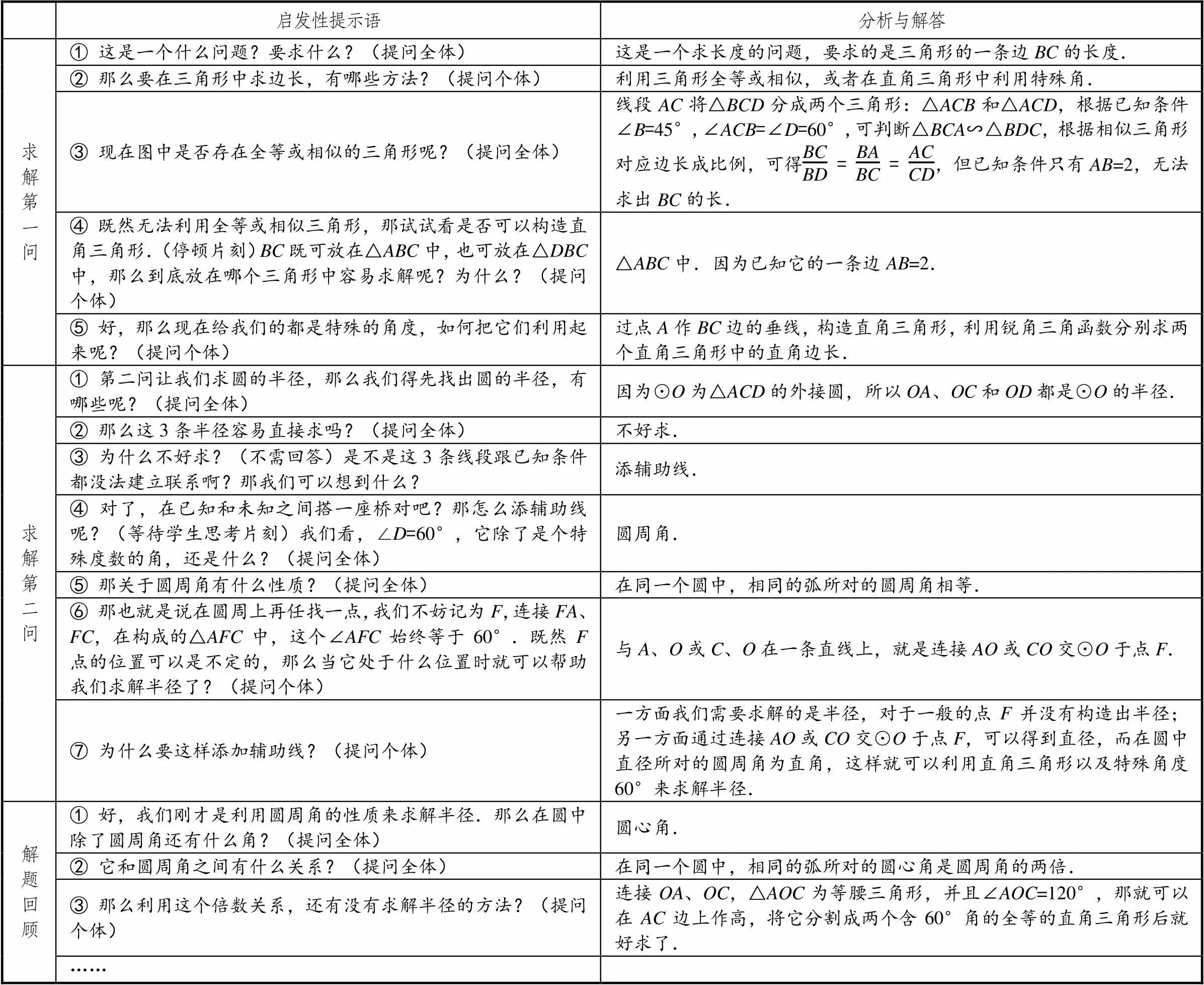
表5 启发性提示语的设计文本（2）

图1 课件设计

6 结束语

数学是思维的科学．数学解题活动是数学的思维活动．数学解题教学应聚焦思维活动过程，致力于教学生学习解题．因而，数学解题教学的教学，应有之义是围绕教学的主要任务——教职前数学教师学习如何教学生学习解题，遵循数学思维活动的规律，进行教学文本和活动的设计．

图2 板书设计

[1] 罗增儒，罗新兵．作为数学教育任务的数学解题[J]．数学教育学报，2005，14（1）：12–15．

[2] 涂荣豹．数学解题的有意义学习[J]．数学教育学报，2001，10（4）：15–20．

[3] 邵光华．论数学解题教学的误区及教学策略[J]．课程·教材·教法，1999，19（5）：22–24．

[4] 沈南山．发掘元认知实现对波利亚解题思想的超越[J]．数学教育学报，2001，10（3）：40–42．

[5] 涂荣豹．数学解题学习中的元认知[J]．数学教育学报，2002，11（4）：6–11．

[6] 涂荣豹，王光明，宁连华．新编数学教学论[M]．上海：华东师范大学出版社，2006：120，124–125．

[7] 韩龙淑，涂荣豹．数学启发式教学中的偏差现象及应对策略[J]．中国教育学刊，2006（10）：66–68．

[8] 董荣森．“启发性提示语”的追溯、发展及其应用[J]．数学通报，2012，51（3）：13–15．

[9] 董荣森．启发性提示语在解题中的应用[J]．江苏教育，2015（22）：37–39．

[10] 韩龙淑．专家型教师与熟手教师运用元认知提示语的数学课堂比较研究[J]．数学教育学报，2016，25（4）：59–62．

[11] 黄红梅．基于波利亚元认知提示语的解题教学案例实录及分析[J]．内蒙古师范大学学报（教育科学版），2017，30（1）：106–109．

[12] 乔治·波利亚．数学的发现——对解题的理解、研究和讲授[M]．刘景麟，译．北京：科学出版社，2006：viii．

[13] 范良火．教师教学知识发展研究（第二版）[M]．上海：华东师范大学出版社，2013：48．

[14] 张景中，彭翕成，邹宇．几何机器明证引发的思考[J]．数学教育学报，2020，29（1）：1-5．

[15] 黄秦安，黄晓林．论数学教育社会学的“理论背景”“体系建构”与“实践价值”[J]．数学教育学报，2020，29（2）：1-5．

[16] 李艳，徐章韬．数学教育实证研究类型及问题表述[J]．数学教育学报，2020，29（2）：6-10．

[17] 马文杰．反思与“重构”数学学习错误矫正原则[J]．数学教育学报，2020，29（2）：11-17．

[18] 刘喆，苏新冰，杜炫杰．智慧教室环境下的数学课堂教学行为研究[J]．数学教育学报，2020，29（4）：44-51．

[19] 曹广福，刘丹．课题式教学法探析[J]．数学教育学报，2020，29（3）：32-36．

On the Teaching for Mathematical Problem Solving

LU Jun1, HU Qing-ying2

(1.Soochow University, School of Mathematical Sciences, Jiangsu Suzhou 215006, China;2. Central Primary School of Si’an Town of Changxing, Zhejiang Huzhou 313113, China)

The main purpose of teaching for mathematical problem solving is to help students become problem solvers. Learning to teach for mathematical problem-solving is to help preservice mathematics teachers how to teach their students for problem solving. Preservice mathematics teachers face two challenges when they learn to teach for problem solving: a) transform from “able to solving” to “able to teach how to solve,” and b) transform from “able to teach how to solve” to “able to teach how students can learn to solve.”. Teaching heuristic prompts, model lessons, and board design of instructional presentations can all be used to foster preservice teachers’ learning to teach for students’ problem solving.

teaching for problem solving; teach how students can learn to solve; heuristic prompts; model lessons; board design of instructional presentations

G451

A

1004–9894（2021）02–0055–06

陆珺，胡晴颖．论数学解题教学的教学[J]．数学教育学报，2021，30（2）：55-60．

2020–10–08

国家社科基金教育学一般课题——中学生学科核心素养的评价研究（BHA170150）

陆珺（1984—），女，江苏苏州人，博士，主要从事数学课程与教学论、数学教师教育研究．

[责任编校：周学智、陈汉君]