口语报告法及其在数学教育研究中的应用述评
2021-04-30勇熊
张 勇熊 斌
口语报告法及其在数学教育研究中的应用述评
张 勇1,2,熊 斌1,2
(1.华东师范大学 数学科学学院,上海 200241;2.上海市核心数学与实践重点实验室,上海 200241)
口语报告法是研究认知过程的基本方法.口语报告法的实施一般包括任务设计、记录口语报告、编码分析和结果汇报.口语报告反应性的元分析表明:出声思考不改变思维过程,与其它类型的口语报告性质不同,出声思考口语报告的客观性更强.口语报告法可广泛用于旨在探求规律或解释现象的基础研究和旨在解决实践问题的应用研究;国内数学教育研究者对口语报告法的研究成果相对零散孤立;国内外已有研究存在用出声思考泛指同时性口语报告、口语报告的收集和分析不严谨等问题.今后的研究应详细说明口语报告的程序和编码信度的建立过程.
认知过程;口语报告;口语记录分析;出声思考;数学教育
1 问题提出
记录被试在实验时或实验之后对自己思维活动进程的口头报告(verbal reports),并将其作为数据资料加以分析的口语报告法(verbal protocol analysis,也译作口语报告分析法、口语记录分析法等)是认知心理学的基本研究方法,被广泛用于各个领域认知过程的研究[1].国内学者在相关教材中大都提及该法[2–4],对方法进展和应用也做了一定程度的述评[5–8].然而,细读可发现已有文献对口语报告法的介绍失之简略,并且存在一些混淆和误解.
混淆和误解主要包括以下几种情况.(1)混淆口语报告与出声思考,将两者等同[3].然而,口语报告有不同的方式和类别[9],出声思考只是其中一种.(2)混淆口语报告与内省,认为“口语报告法从其实质而言,仍是一种内省法”[5].而口语报告理论的创立者指出“获取口语报告的出声思考法与内省法性质不同”[10].(3)误解出声思考法的首创者.王甦和汪安圣编著的《认知心理学》是国内早期颇有影响的教材,书中指出“这种出声思考的方法是由德国心理学家Duncker(1945)首先发展出来的,后来Newell和Simon(1972)在研究问题解决时,把它当作一个重要的方法加以应用”[2].研究者多直接援引此说法或将前半句误解为Duncker于1945年首先提出该方法.事实上,Duncker于1940年离世[11],1945年的说法源于其影响广泛的英译本著作[12].Duncker(1926)已运用该法[13],反对内省的行为主义心理学家Watson(1920)就对出声思考做过探讨[14].出现上述现象的原因可能是当时难以检索原始文献,建立口语报告理论基础的文献[1]曾是西方心理学权威期刊《心理学评论》()刊载的引用率最高的20篇论文之一[15],并未列入前述教材的参考文献之中.另外,口语报告法虽被广泛应用,国外学者却对其效度一直存在争议,对其与内省的关系的认识亦有分歧,需要不断积累实证数据以考察口语报告法的有效性.
鉴于上述分析,研究者从方法本身和方法应用两个方面总结口语报告法的研究进展,为其他研究者正确认识和使用方法提供参考.其中方法本身部分主要参考权威的心理学研究,概述口语报告的发展历史、原理与类型、争议与进展、适用范围与实施程序;方法应用部分偏重数学教育研究,梳理口语报告法在数学教育研究各个领域的应用,总结已有研究在方法应用上存在的分歧和问题,并对方法应用和未来研究提出建议.
2 口语报告法概述
2.1 方法发展的历史回顾
口语报告法源于心理学研究中的内省(introspection,又叫“自我观察法”).德国心理学家Wundt率先把实验法引进心理学,将经验性、日常生活性的内省发展为实验内省.在这个方法中,经过充分训练的观察者在严格控制的条件下报告自己的意识内容.内省研究在取得成功的同时也不断遇到麻烦,不同的实验室相继提出不同类型的内省.由于作为研究数据的意识内容只有执行思维过程的观察者本人可以访问,这导致无法重复实证研究,削弱了研究结果的可靠性.内省法的局限导致了行为主义的兴起,心理学的主流研究从聚焦内省观察转向关注外在行为.与此同时,仍有研究者继续使用内省法的各种变体,主要的方法论进展是把口语报告而不是意识内容当作数据[16].这些数据可供其他研究者检查和解释,提高了研究的客观性和可重复性.“让被试在解决问题或执行任务的同时大声说出头脑中想法的”的出声思考法(think aloud method)作为收集口语报告的技术之一,被Duncker等学者使用并取得系列成果.
20世纪六七十年代,认知心理学迅速发展,研究者们对提供认知过程数据的方法重新产生兴趣,促进了口语报告理论基础的发展.其中,Newell和Simon把出声思考法作为数据收集的基本方法,通过对被试口语报告的纵向分析,归纳出解决问题者所应用的过程,并能据此编制计算机可执行的程序,推动了口语报告方法的合法化.Nisbett和Wilson(1977)对高级心理过程口语报告准确性的经典述评[17]引发了对口语报告效度的广泛讨论,亟待确定在何种条件下可以获得可靠和有效的口头报告数据.之后,Ericsson和Simon(1980)利用信息加工理论阐释口语报告的生成机制和不同类型口语报告对被试思维过程的影响,并在详尽述评相关文献的基础上将论文扩充为著作[18].至此,口语报告的方法论基础得以确立.
2.2 口语报告的原理与类型
先通过一个简化的人类记忆模型解释口语报告的工作原理,然后介绍口语报告的不同类型及其差异.
图1是基于人类认知系统的一个简单模型,解释了外界信息从感觉系统转移到内在系统,以及内在信息言语化的过程[16].模型右端的长时记忆是知识被永久储存的部分,左端是将环境中的信息转化为内在形式的感觉系统,工作记忆是当前“活跃”信息驻留的部分.模型中有5个过程.①感知,信息从感觉缓冲区进入工作记忆.②检索,信息从长时记忆检索到工作记忆中.③建构,工作记忆中的信息可以建构新的信息.例如,解题时在概念之间建立新的联系并将其作为一个对象存储在工作记忆中.④存储,将工作记忆中的信息存储到长时记忆中.⑤言语化,工作记忆中的信息被转换成话语,输出口语记录.

图1 口语报告的记忆模型
根据过程⑤发生的时间可将口语报告分为:任务解决过程中收集的同时性口语报告,任务完成后收集的追述性口语报告.两类口语报告的性质存在差异,同时性口语报告的内容是工作记忆中信息的子集,而追述性口语报告涉及过程④和②,即信息的存储和检索,容易因记忆错误导致无效和不完整的数据.
同时性口语报告可能是工作记忆中当前正在执行的任务信息的直接表达,也可能是对这些信息进行中间处理后的产物.Ericsson和Simon[1,18]将同时性口语报告划分为3种水平.水平1的言语化(level 1 verbalization)指直接表达存储在语言代码中的信息;水平2的言语化(level 2 verbalization)指无需额外处理过程的信息的表达,对其进行语言编码后即可表达为口语;水平3的言语化(level 3 verbalization)指对信息经过扫描、过滤、推理或生成过程后的口语表达,主试通常会在任务执行过程中给予被试不同程度的提问或提示.
2.3 口语报告的争议与进展
口语报告的争议主要围绕3个重要问题[19]:(1)口语报告是否能够准确反映被试的思维过程——效度问题;(2)要求被试报告自己的想法是否会改变其思维过程——反应性问题;(3)口语报告是否能像其它行为数据一样被客观对待.Ericsson等研究者解决争议的基本思路是基于信息加工理论,区分各种类型的口语报告,并对其有效性做出预测,进一步的发展则依赖于实证研究提供证据,以检验预测的可靠性.下面简要介绍有关研究进展.
首先看追述性口语报告.Nisbett和Wilson[17]已经证明,在识别决定行为的重要情境因素时,被试对自己行为动机的追述并不比外在观察者更准确.事后解释行为动机往往掺杂了对已发生事件的回忆和额外推理,难以保证效度.另外,要求被试给出规定类型的口语报告也会引发额外推理,甚至对回忆具有破坏性.言语遮蔽(verbal overshadowing)的研究[20]表明,明确告知被试如何口头描述先前看到的视觉刺激(如人脸)会损害之后对刺激的识别.理想情况下,追述性口语报告由被试完成任务后立刻给出,常用指导语是“报告你记住的有关任务的所有想法”.只要求被试回忆想法得到的信息与完成任务过程的其它观察数据相吻合,并且对于用时很短(1~5秒)的任务,回忆甚至比出声思考更完整[21].
其次看同时性口语报告.Ericsson和Simon[1,18]指出:水平1和水平2的言语化是被试在集中精力完成任务时头脑中并发想法的直接表达,不会改变被试的认知过程,两者可统称为出声思考口语报告;水平3的言语化要求解释或描述特定信息,会引起被试对原有想法的进一步加工,从而改变思维过程和行为表现.因理论提出之初实证研究较少,对上述预测的论证是举例式的.建立口语报告理论基础的文献[1]发表30年之后,研究者得以对积累的实验研究作系统的元分析.Ericsson等[22]对包含近3 500名被试的94项研究的元分析表明:出声思考组和沉默控制组执行任务的表现无显著差异,即便对任务类型等因素作统计控制后依然如此;相比之下,要求被试解释或描述想法和行为具有显著的反应性,导致比沉默控制组更好的表现;所有的口头报告程序都倾向于增加完成任务的时间.有研究者明确指出“出声思考不是内省法的一种表现形式,而是与其性质不同的方法”[10],建议今后的研究将出声思考与其它口语报告方法区别对待.
综上可得:出声思考口语报告的客观性更强,能反映被试即时经历的思维过程,适合从信息加工的视角对思维进行纯认知的研究;仅要求被试回忆思维过程的追述性口语报告退而次之,在任务耗时较短时更可靠;需要被试解释或描述想法和行为的其它类型的口语报告具有反应性,对发展学生思维和改进教学实践具有重要启示.
2.4 适用范围与实施要点
口语报告法有其局限性与适用的任务范围.由图1的记忆模型可知,被试注意到的信息是直接发声的或者是进行言语编码后发声的.因此,口语报告无法揭示以下两种认知类型:已经变得自动化的过程,不以言语编码或难以转变为言语编码的思维.口语报告法最适合研究定义良好的任务.这类任务大多可作任务分析,即基于被试的已有知识和技能,对获得答案的可能的中介过程进行正式的理论分析.
口语报告法的实施一般包括任务设计、记录口语报告、编码分析和结果汇报4个方面,具体流程见图2[23].除Ericsson和Simon外,其他研究者使用口语报告法的经验也值得借鉴,详细信息可进一步查阅原文[16,24].下面简要介绍图2各个阶段的实施要点.
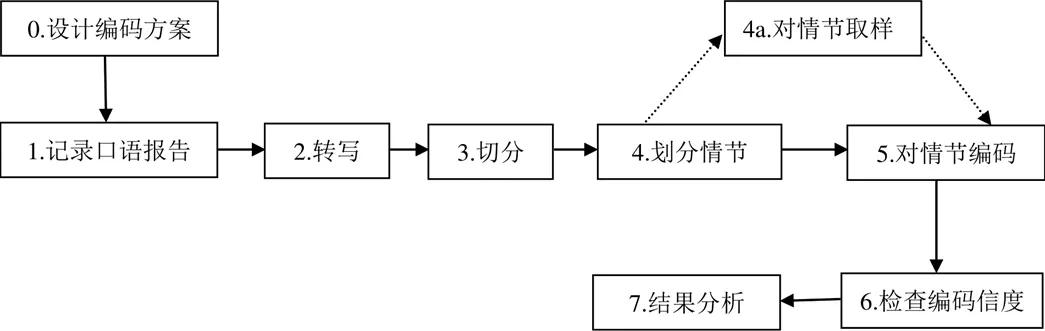
图2 口语报告的分析流程
设计编码方案(阶段0):建立有效和可靠的编码方案是口语报告分析的核心,编码方案可以是事先确定的非语境编码或基于口语报告构建的语境编码.编码方案的开发通常是一个高度迭代的过程,不论在研究的哪个阶段,都要仔细考量或改进编码方案,以符合研究的具体情况.
记录口语报告(阶段1):应详细说明口语报告的程序——包括指导语、提示的类型、主试和被试的互动以及口语报告组和沉默控制组之间的差异[22].若采用出声思考法,应对被试进行充分的培训(培训任务可与目标任务相近或无关,具体差异有待考查),当被试沉默超过预定时间,应提示被试“继续说”而不是“你正在想什么”.
口语报告编码(阶段2~4):转写(阶段2)必须忠实客观,避免任何重组、风格和语法的改进.切分(阶段3)的依据是句子的意思,所分的每一段都应有一个独立的思维主题,而不管这些句子是否都完整及合乎语法.经验表明,边听边切分口语报告的人之间存在高度的一致性.切分的片段常常组合成情节(阶段4),一个情节就是一个片段序列.
口语报告编码(阶段4a~6):口语报告若包含很多情节,可先对情节取样,再由两位编码人员独立编码,并计算编码者信度.取样情节应具有代表性,取样比例取决于转写文本的特点和编码方案.若代码在转写文本中出现频繁,可选择较小比例(20%~25%)的情节双编码,反之应扩大取样比例[23].
编码者信度(inter-coder reliability)是指不同编码者分配给同一数据的代码之间的相关性.常用方法是计算编码一致的实例数占所有代码实例的百分比.这种度量对不同类别代码所占比例的差异很敏感,易导致编码一致性的夸大,建议用Cohen[25]的kappa系数校正,并汇报两种指标.若信度不理想,应完善编码方案,重新进行阶段4a~6.下面以一个简化的例子说明两种指标的计算方法及差异,更复杂的例子和分析参见文献[16].
例 一份较短的口语报告被划分为8个情节,编码方案包含A、B两个代码,甲、乙二人对8个情节独立编码的结果如表1所示.

表1 甲乙的编码情况
由表1可知,甲、乙将5个情节共同编码为A,将一个情节共同编码为B.故二人编码的实际一致率为(5+1)/8=0.75.由表1也可看出,甲、乙对代码A的使用更频繁,这意味着一个情节被编码为A的几率更大.为校正不同代码所占比例差异较大造成的影响,可进一步计算kappa系数,公式如下:
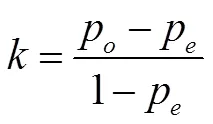
p为两人编码的实际一致率,即0.75;p为两人编码的机遇一致率,即将情节共同编码为A或B的几率之和,p=7/8×5/8+1/8×3/8≈0.60.故

结果分析与报告(阶段7):建立编码信度并对所有数据进行编码后,根据研究问题和目标,可以用定量或定性方法继续对数据进行分析.分析结果应以何种方式在论文中报告,尚无完全一致的意见.应尽量在其他研究者能够重复分析结果的程度和期刊的版面限制之间取得平衡.
3 数学教育研究中的口语报告法
顾泠沅、杨玉东[26]将数学教育研究的各种目的归结为两类:理论的目的和实践的目的.前者旨在探求规律或解释现象,后者以解决实践中的问题为直接目的.据此,将口语报告的有关研究粗略分为理论导向的基础研究和实践导向的应用研究.基础研究重在描述认知过程及个体差异,试图建构认知模型以揭示思维规律;应用研究旨在开发服务教学的产品(如测评工具、课程材料等),或者为改进数学教学提供直接指导.下面对两类研究涵盖的主题、研究成果及近期发展作简要述评;结合口语报告的方法学研究,指出已有研究在方法应用上存在的分歧和问题,对方法应用和未来研究提出建议.
3.1 口语报告法的基础研究
数学问题解决是口语报告法应用最频繁的领域之一.口语报告法可用来调查问题解决能力的个体差异、任务难度的差异、教学效果和影响问题解决的因素.代表性成果当属克鲁捷茨基对数学能力结构的研究和20世纪80年代的西方数学问题解决研究.克鲁捷茨基[27]研究数学能力的实验方法是编制一些专为实验用的数学题,让具有不同数学能力的学生以出声思考的方式解答,然后进行质和量的分析.Lester[28]回顾了1970—1994年间的数学问题解决研究,概括出各阶段研究的关注点和方法论(见表2).

表2 数学问题解决研究的关注点与方法论
由表2可知,“出声思考”口语报告分析是20世纪80年代问题解决研究的主流方法,90年代中期后,问题解决研究的热潮退却.口语报告法仍是研究问题解决及相关主题的重要方法.“证明”即是一个重要领域,有研究者利用口语报告法对不同被试群体构建、阅读、理解、评价证明的思维过程作了大量研究[29].
口语报告法是研究教师认知与决策的重要方法.教师认知与决策研究兴起于20世纪70年代,到90年代成为教学研究最重要的领域之一[30].其中,教师在教学计划阶段的思维和教学中的交互思维是研究者普遍关注的两类问题.为回答“当教师在进行教学设计时,他们在想些什么”这一问题,出声思考技术被广泛应用.教师对教学计划的出声思考口语报告是主要的证据来源.大量研究发现:许多教师在教学设计时集中于内容和教学活动,而不是集中于目标和学生的个体差异.教学实践和教学计划之间的矛盾的揭示对教学改进有重要启示.对教学中交互思维的研究常采用刺激回忆和录像带分析等技术,被研究的教师通过观察录像带和回忆来描述产生特定教学行为的思维过程.教师此时的口头报告可归为回忆和解释并存的追述性口语报告.
除数学问题解决、证明、教师认知与决策等重要研究外,口语报告法可对数学教育各方面的议题展开研究.由于这些议题尚未像数学问题解决那样取得系统成果,研究者仅对近年来发展较快的数学问题提出研究作简要介绍.蔡金法等[31]梳理出问题提出研究的十大问题,其中第四个问题为“我们对数学问题提出的认知过程了解多少”.以出声思考为主的口语报告法是回答该问题的基本方法,但相关研究很少.“台球任务”是一个典型案例.蔡金法等[32]分析了两位本科生在台球任务中提出和解决数学问题的口语报告,揭示出被试在开放的问题情境中进行数学探究的若干特点.Kontorovich等[33]以台球任务为刺激情境,让一位数学竞赛命题专家以出声思考的方式提出尽可能多的数学问题,对专家提出系列题目的组织原则作了探讨.回顾数学问题解决研究的历史,可以预期口语报告法将在不同被试群体完成各类问题提出任务的研究中得到广泛应用.
认知心理学在20世纪80年代初被介绍到中国,中科院心理所的朱新明[34]与Simon有过合作研究,是国内使用出声思考法研究几何问题解决的先驱,推动了口语报告法在中国的传播和应用.与国外同行及国内的心理学研究者相比,国内数学教育研究者对口语报告法的使用明显较少,研究成果相对零散孤立.相关基础研究主要有:青浦县数学教改实验小组[35]对180名学生开展的问题探究的出声思考实验;连四清[36]对学生解题思维障碍排除的研究;李祥兆[37]对数学归纳推理认知过程的研究;李明振等[38]对数学建模认知过程及特点的研究;杨豫晖[39]对数学教师教学决策的研究;何忆捷[40]对高中资优生利用构造法解决数学问题特点的研究.另外,国内学者对出声思考的使用不严格,国外相关研究也存在类似问题.相关问题及改进建议将在3.3节作具体阐述.
3.2 口语报告法的应用研究
本节主要介绍口语报告法在数学教育评价和数学教学实践中的应用.数学教育评价部分涉及元认知测评、问卷和测试改进、课程材料的使用和开发;数学教学实践部分将口语报告法作为教学手段和学习策略,揭示其对改进数学教学的应用价值.
从20世纪80年代早期开始,元认知作为影响问题解决和数学表现的关键因素日益受到关注.元认知测评是研究热点之一,测评方式包括离线(off-line)测量和在线(on-line)测量[41].前者指任务执行之前或之后进行的问卷和访谈,后者通过任务执行期间的观察、出声思考口语报告等过程数据做出评估.然而,人们对两类评估方法的有效性知之甚少.Veenman等[42]最近的研究表明,对元认知技能的测评,在线方法优于离线方法,回顾性问卷比前瞻性问卷稍好.国内学者在元认知的“离线”测评方面做了许多工作,开发了适合不同年龄阶段的问卷[43–45].进一步可采用出声思考在内的多元方法检验和改进已有测评工具.
口语报告法是设计和改进问卷的重要工具.目前被广泛引用的问题——作答模型包括4个阶段:理解、检索、判断和作答.该模型有助于理解问卷作答过程的复杂性以及作答误差的大量可能性[46].Anderson[47]以一个演绎推理任务为例,说明同时性口语报告可揭示被试对任务的理解以及通过错误推理得出正确回答的情况.Güss[48]总结了出声思考在提高跨文化调查问卷效度中的应用.出声思考数据可使问题更明确易懂,改进敏感话题的题项表述.类似地,口语报告法也有助于改进命题工作.让学生出声思考完成测试既可发现试题背景、语言表述等方面存在的问题,也能深化对特定题型考查功能的认识.Roth等[49]使用专家分析和出声思考两种方法探讨PISA数学试题的语言背景对少数民族学生答题的影响,指出学生的出声思考口语报告可为解释成绩差异提供新的见解.口语报告法也用于研究评分过程[50],有利于提高阅卷的科学性和公平性.
口语报告法亦被用于课程或教学材料的开发.Svenson等[51]调查了两名本科生和一名研究生如何使用课程材料完成数学习题,出声思考口语报告揭示出学生使用课程材料的差异(查找例证vs查找定义)以及学习中存在的问题.Shepherd等[52]调查了11名学生阅读数学教材新篇章时的行为和困难,学生被要求在积极阅读的间隙出声思考,研究结果表明:学生对教材的阅读和使用并不理想.Cowan[53]以令人信服的证据表明出声思考技术可以揭示出学生对课程材料的反常使用(相对编者的预期而言)和材料中存在的问题,从而有助于教师和课程设计者开发学生友好型的课程资源.另外,口语报告法很早就被用于人机互动界面的改进以及产品的可用性测试.信息技术的快速发展驱动了电子教科书及其平台的开发,各种在线学习平台和APP层出不穷.收集用户在平台或软件中实施任务的出声思考口语报告有助于产品的迭代改进.
让学生口头报告思考过程并给予相应提示或指导的有效性,已被学习策略训练的实验研究证实[54].除用于专门的实验干预,口语报告法也可作为日常的教学手段和学习策略[55],贯彻“让学生看到思维过程”的主体性教学原则[56].一方面教师可结合典型内容给学生示范如何出声思考,甚至对学生的疑问现想现推,把自己的解题思路包括失败的思路暴露给学生,让学生看到教师的思维过程;另一方面,在教学中可通过适当的提问和提示,引导学生生成描述和解释思维过程的口语报告,这样既能提高学生的元认知水平,也有助于教师基于学生理解做出教学决策.口语报告法在数学教学中的应用有待细化和深化,不同水平和类型的口语报告都有用武之地.比如,与水平3言语化关系密切的自我解释[57](为自己生成解释以试图理解新信息)可有效促进理解,是一个值得关注的研究方向.
3.3 方法应用的问题与建议
数学教育研究者应用口语报告法的分歧和问题主要体现在对出声思考的界定和使用上.
Ericsson等[1]将被试在集中精力完成任务时头脑中并发想法的直接表达称作出声思考.研究者有时扩大其范围,用出声思考泛指同时性口语报告.表2中的“出声思考”即是如此,合作解题和基于任务的访谈情景下获得的口语报告也被涵盖在内.比如:(1)Schoenfeld[58]的研究中,学生多为两人一组合作解题.具有对话性质的合作解题容易引发解释或描述想法的水平3的言语化,显然不同于单个被试的出声思考.(2)Clement[59]研究经典的学生—教授问题时将出声思考整合进临床访谈(原文方法部分有如下措辞:研究者对15名大学新生进行临床访谈,要求他们在解决学生—教授问题和类似问题时出声思考,并录音和录像),这种情况下主试会依被试表现灵活提问,也有别于非干预性的出声思考.
一些研究者虽援引Ericsson对出声思考的界定,但方法的使用存在不规范和不严谨之处.指导语和提示语方面的主要问题有:论文方法部分过于简略,只是提及让被试出声思考,未报告具体的指导语和如何培训被试;被试停止出声思考时,提问“你正在想什么”,这样的提示语可能引发被试自我观察或者生成面向他人的想法描述,从而改变后续的思维过程.口语报告编码方面的主要问题是:没有清晰的编码方案,主要以举例的形式使用口语记录;未进行双重编码或者未汇报编码信度.
对同时性口语报告的反应性作元分析时,Ericsson等[22]将纳入文献的口头报告程序分为4类:出声思考(think- aloud)、解释的(explanatory)、定向的(directed)、不明确的(unspecified).照此标准,大部分运用口语报告法的数学教育研究将归入后3类.元分析的结果表明:要求被试解释或描述想法和行为具有显著的反应性,导致比沉默控制组更好的表现.据此,应审慎看待已有研究数据的可靠性,当研究目的是基于口语报告建立解释被试行为的认知模型时更应如此.出声思考技术获得的数据准确但不够完整,不同程度的提问探测可使数据更丰富,但面临着数据失真的风险.建议研究者在使用口语报告法时通盘考虑研究目的、被试背景和任务特征,在数据的丰富性和准确性之间取得平衡.运用口语报告法时,研究者应详细说明口语报告的程序和编码过程(详见2.4节的实施要点).若采用出声思考法,建议遵循Ericsson等[18,22]提出的标准化程序或近似版本.
4 总结与展望
方法部分概述口语报告方法论的历史进展,通过信息加工理论中的记忆模型说明口语报告的产生机制及不同类型,介绍有关口语报告的争议与进展,总结口语报告法的适用范围和实施要点.主要结果是:被试集中精力完成任务时的出声思考不具有反应性;要求被试解释或描述想法和行为具有显著的反应性;应将出声思考与其它口语报告方法区别对待.第二部分述评口语报告法在数学教育研究中的应用、存在的问题与改进建议.主要结果是:口语报告法可广泛用于旨在探求规律或解释现象的基础研究和旨在解决实践问题的应用研究;国内数学教育研究者对口语报告法的使用不足,研究成果相对零散孤立;国内外已有研究存在用出声思考泛指同时性口语报告、口语报告的收集和分析不严谨等问题.建议遵循Ericsson等学者对出声思考的界定及其推荐的口头报告程序.
未来需要继续加强口语报告的方法学研究,为研究不同被试群体和任务类型提供方法指南.当前比较明确的结论是出声思考口语报告反应性低、准确性高.应进一步探究出声思考的操作细节对数据质量的影响(比如在培训被试熟悉出声思考时,有研究者使用与实验任务相近的任务,而Ericsson推荐的是无关任务,两者差异何在)和通用编码方案的开发,以促进方法操作的标准化和研究成果的交流.基于任务的访谈源自皮亚杰的临床访谈[60],主试根据被试表现给出提问和提示可获得比出声思考更丰富的数据,但难以判断数据的准确性.如何在数据的可靠性和丰富性之间取得平衡值得深入研究.鉴于已有方法学研究以西方被试为主,不可想当然地将相关结论推广到其它文化背景的被试中.国内数学教育研究者不仅要关注口语报告方法学的研究进展,更要加强方法的本土研究,不断积累可靠的研究数据,争取对相关争议做出自己的元分析.
口语报告法在数学教育研究中的应用也有待进一步加强.未来基础研究的重点是使用口语报告法对各个数学专题的学习过程作深入细致的调查,为数学学习理论的归纳奠定可靠基础;至于应用研究,一方面应加强口语报告法在数学教育评价中的应用,比如数学核心素养测评、在线教学资源的开发与改进.另一方面应深化作为教学手段和学习策略的口语报告法的研究.比如,进一步厘清解释或描述想法的各类口语报告对改善学生数学表现的差异,帮助教师改进课堂提问,让师生的交流更具思维含量;设计可引发自我解释的课堂任务或课后练习以提高学生的反思和理解水平.总之,口语报告法具有研究工具和教学工具的双重价值.虽然收集、处理和分析口语报告耗时耗力,但其提供的有关思维过程的丰富数据值得这种付出.对口语报告法的耐心使用有助于理解数学教学涉及的各种现象和过程,研究成果的不断积累最终将促成理论的归纳和实践的改进.
[1] ERICSSON K A, SIMON H A. Verbal reports as data [J]. Psychological Review, 1980, 87 (3): 215–251.
[2] 王甦,汪安圣.认知心理学[M].北京:北京大学出版社,1992:14–16.
[3] 张庆林,邱江.思维心理学[M].重庆:西南师范大学出版社,2007:14–15.
[4] 邵志芳.思维心理学[M].2版.上海:华东师范大学出版社,2007:25–30.
[5] 任洁,许尚侠.当代心理学对口语报告的研究评述[J].心理科学,1998,21(1):77–78.
[6] 李亦菲,朱新明.一种通用的口语报告编码方案[J].心理学动态,1998,6(4):47–51.
[7] 李贤,余嘉元.国内外学者视角中的口语报告方法[J].苏州大学学报(哲学社会科学版),2006(1):119–121.
[8] 陈英和,王治国.口语报告法在阅读策略研究中的应用[J].心理科学,2006(6):25–27,38.
[9] 司马贺.人类的认知:思维的信息加工理论[M].荆其诚,张厚粲,译.北京:科学出版社,1986:85–89.
[10] ERICSSON K A, FOX M C. Thinking aloud is not a form of introspection but a qualitatively different methodology: Reply to Schooler (2011) [J]. Psychological Bulletin, 2011, 137 (2): 351–354.
[11] SCHNALL S. Life as the problem: Karl Dunckers’ context [J]. Papers on the History of Psychology, 1999, 1 (2): 13–28.
[12] DUNCKER K. On problem-solving (Lees L S, Trans.) [J]. Psychological Monographs, 1945, 58 (5): 1–113.
[13] DUNCKER K. A qualitative (experimental and theoretical) study of productive thinking (solving of comprehensible problems) [J]. The Pedagogical Seminary and Journal of Genetic Psychology, 1926, 33 (4): 642–708.
[14] WATSON J B. Is thinking merely the action of language mechanisms? [J]. British Journal of Psychology, 1920 (11): 87–104.
[15] KINTSCH W, CACIOPPO J T. Introduction to the 100th anniversary issue of the[J]. Psychological Review, 1994, 101 (2): 195–199.
[16] van SOMEREN M W, BARNARD Y F, SANDBERG J A. The think aloud method: A practical guide to modeling cognitive processes [M]. London: Academic Press, 1994: 29–33.
[17] NISBETT R E, WILSON T D. Telling more than we can know: Verbal reports on mental processes [J]. Psychological Review, 1977, 84 (3): 231–259.
[18] ERICSSON K A, SIMON H A. Protocol analysis: Verbal reports as data (Rev. ed.) [M]. Cambridge, MA: MIT Press, 1993: 1.
[19] CRUTCHER R J. Telling what we know: The use of verbal report methodologies in psychological research [J]. Psychological Science, 1994, 5 (5): 241–244.
[20] SCHOOLER J W, ENGSTLER-SCHOOLER T Y. Verbal overshadowing of visual memories: Some things are better left unsaid [J]. Cognitive Psychology, 1990, 22 (1): 36–71.
[21] ERICSSON K A. Valid and non-reactive verbalization of thoughts during performance of tasks: Towards a solution to the central problems of introspection as a source of scientific data [J]. Journal of Consciousness Studies, 2003, 10 (9–10): 1–18.
[22] FOX M C, Ericsson K A, Best R. Do procedures for verbal reporting of thinking have to be reactive? A meta-analysis and recommendations for best reporting methods [J]. Psychological Bulletin, 2011, 137 (2): 316–344.
[23] HUGHES J, PARKES S. Trends in the use of verbal protocol analysis in software engineering research [J]. Behaviour & Information Technology, 2003, 22 (2): 127–140.
[24] CHI M T. Quantifying qualitative analyses of verbal data: A practical guide [J]. The Journal of the Learning Sciences, 1997, 6 (3): 271–315.
[25] COHEN J. A coefficient of agreement for nominal scales [J]. Educational and Psychological Measurement, 1960, 20 (1): 37–46.
[26] 顾泠沅,杨玉东.反思数学教育研究的目的与方法[J].数学教育学报,2003,12(2):10–12.
[27] 克鲁捷茨基.中小学生数学能力心理学[M].李伯黍,洪宝林,译.上海:上海教育出版社,1983:103.
[28] LESTER F K. Musings about mathematical problem-solving research: 1970—1994 [J]. Journal for Research in Mathematics Education, 1994, 25 (6): 660–675.
[29] STYLIANIDES G, STYLIANIDES A, WEBER K. Research on the teaching and learning of proof: Taking stock and moving forward [M] // CAI J. Compendium for research in mathematics education. Reston: National Council of Teachers of Mathematics, 2017: 237–266.
[30] 顾泠沅,易凌峰,聂必凯.寻找中间地带:国际数学教育改革的大趋势[M].上海:上海教育出版社,2003:154–161.
[31] CAI J, HWANG S, JIANG C, et al. Problem posing research in mathematics: Some answered and unanswered questions [M] // SINGER F M, ALLERTON N, CAI J. Mathematical problem posing: From research to effective practice. New York: Springer, 2015: 3–34.
[32] CAI J, CIFARELLI V V. Exploring mathematical exploration: How two college students formulated and solved their own mathematical problems [J]. Focus on Learning Problems in Mathematics, 2005, 27 (3): 43–72.
[33] KONTOROVICH I, KOICU B. A case study of an expert problem poser for mathematics competitions [J]. International Journal of Science & Mathematics Education, 2016, 14 (1): 81–99.
[34] 朱新明.解决几何问题的思维过程[J].心理学报,1983(1):11–20.
[35] 青浦县数学教改实验小组.数学教改实验的基本过程及其研究方法[J].数学教育学报,1992,1(1):1–10.
[36] 连四清.思维障碍的排除[J].中国教育学刊,2000(2):47–49.
[37] 李祥兆.数学归纳推理的认知过程研究[J].数学教育学报,2005,14(2):67–70.
[38] 李明振,喻平,宋乃庆.数学建模的一般认知过程研究[J].数学教育学报,2008,17(6):45–48.
[39] 杨豫晖.数学教师教学决策研究[D].重庆:西南大学,2009:1.
[40] 何忆捷.高中数学资优生运用构造法解决数学问题的个案研究[D].上海:华东师范大学,2017:1.
[41] SCHNEIDER W, ARTELT C. Metacognition and mathematics education [J]. ZDM, 2010, 42 (2): 149–161.
[42] VEENMAN M V, CLEEF D V. Measuring metacognitive skills for mathematics: students’ self-reports versus on-line assessment methods [J]. ZDM, 2019, 51 (4): 691–701.
[43] 唐剑岚,周莹,汤服成.数学问题解决中的元认知问卷量表的设计[J].数学教育学报,2005,14(4):44–48.
[44] 王光明,佘文娟,王兆云.高中生数学元认知水平调查问卷的设计与编制[J].心理与行为研究,2016(2):152–161.
[45] 崔宝蕊,李健,王光明.初中生数学元认知水平调查问卷的设计与编制[J].数学教育学报,2018,27(3):45–51.
[46] MILLER K, CHEPP V, WILLSON S. Cognitive interviewing methodology [M]. New York: John Wiley and Sons, 2014: 1–2.
[47] ANDERSON M A. Protocol analysis: A methodology for exploring the information processing of gifted children [J]. Gifted Child Quarterly, 1986, 30 (1): 28–32.
[48] GÜSS C D. What is going through your mind? Thinking aloud as a method in cross-cultural psychology [J]. Frontiers in Psychology, 2018 (9): 1 292.
[49] ROTH W M, ERCIKAN K, SIMON M, et al. The assessment of mathematical literacy of linguistic minority students: Results of a multi-method investigation [J]. The Journal of Mathematical Behavior, 2015 (40): 88–105.
[50] SUTO W M, GREATOREX J. What goes through an examiner’s mind? Using verbal protocols to gain insights into the GCSE marking process [J]. British Educational Research Journal, 2008, 34 (2): 213–233.
[51] SVENSON I F, LAWRENCE J A, WILLIS S G. Distance university students’ processing of mathematics exercises [J]. Educational Studies in Mathematics, 1983, 14 (1): 73–85.
[52] SHEPHERD M D, SELDEN A, SELDEN J. University students’ reading of their first-year mathematics textbooks [J]. Mathematical Thinking and Learning, 2012, 14 (3): 226–256.
[53] COWAN J. The potential of cognitive think-aloud protocols for educational action-research [J]. Active Learning in Higher Education, 2019, 20 (3): 219–232.
[54] 方平,郭春彦,汪玲,等.数学学习策略的实验研究[J].心理发展与教育,2000(1):44–48.
[55] 星宇.出声思考在教学中的应用[J].中国教育学刊,2008(8):54–56.
[56] 胡炯涛.数学教学论[M].南宁:广西教育出版社,1996:12.
[57] RITTLE-JOHNSON B, LOEHR A M, DURKIN K. Promoting self-explanation to improve mathematics learning: A meta-analysis and instructional design principles [J]. ZDM, 2017, 49 (4): 599–611.
[58] SCHOENFELD A H. Making sense of “out loud” problem-solving protocols [J]. The Journal of Mathematical Behavior, 1985, 4 (2): 171–191.
[59] CLEMENT J. Algebra word problem solutions: Thought processes underlying a common misconception [J]. Journal for Research in Mathematics Education, 1982, 13 (1): 16–30.
[60] MAHER C A, SIGLEY R. Task-based interviews in mathematics education [M] // LERNMAN S. Encyclopedia of mathematics education. Dordrecht: Springer, 2014: 579–582.
A Review of Verbal Protocol Analysis and Its Application in Mathematics Education Research
ZHANG Yong1, 2, XIONG Bin1, 2
(1. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;2. Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, Shanghai 200241, China)
Verbal protocol analysis is a basic research methodology for studying cognitive processes. To promote its application, this paper reviews the methodological process of verbal protocol analysis and related mathematical education research. The first part outlines its historical development, principles and types, disadvantages and advantages, scope of application, and implementation procedure. Meta-analysis of the reactivity of verbal reports shows that think-aloud does not change thought processes and is different from other types of verbal reports. It is suggested that future studies should explain verbalization procedures and how to determine inter-coder reliability in detail. The second part of the paper gives a profile of its use within mathematics education research.The existing research is divided into theory-oriented pure research and practice-oriented applied research. Based on the methodological review of verbal reports, this article points out inconsistencies and problems in previous studies and provides suggestions for methodological applications and future research.
cognitive processes; verbal reports; verbal protocol analysis; think aloud; mathematics education
G632.4
A
1004–9894(2021)02–0083–07
张勇,熊斌.口语报告法及其在数学教育研究中的应用述评[J].数学教育学报,2021,30(2):83-89.
2020–10–07
上海市核心数学与实践重点实验室课题——数学实践(18DZ2271000)
张勇(1988—),男,山东泰安人,博士生,主要从事数学方法论与数学教育研究.
[责任编校:陈汉君、陈隽]
