海杂波背景下雷达目标贝叶斯检测算法
2021-04-30许述文王喆祥水鹏朗
许述文,王喆祥,水鹏朗
(西安电子科技大学 雷达信号处理国家重点实验室,陕西 西安 710071)
随着雷达分辨率的提高,中心极限定理的假设不再满足,海杂波呈现出明显的非高斯特性,此时再使用高斯背景下的检测器会造成明显的虚警或漏检[1]。高分辨海杂波通常采用符合高斯模型进行建模,复合高斯模型采用两个独立的过程描述非高斯杂波:零均值复高斯过程的散斑分量和非负随机过程的纹理分量。在一个相干处理间隔内,纹理分量可以看作一个随机常数,此时复合高斯模型退化为球不变随机向量模型。通过将纹理分量建模为服从不同分布的随机变量可以得到不同的杂波模型[2]。当纹理分量分别服从伽马分布、逆伽马分布、逆高斯(Inverse Gaussian,IG)分布时,杂波的幅度分布服从K分布[3]、广义帕累托分布[4]和CG-IG分布[5]。这3种幅度模型经常被用来描述不同分辨率下的海杂波。但是,由于海杂波特性受到如极化方式、擦地角、雷达工作频率等多种条件的影响,以上3种杂波模型的适用范围不够广,同时实测数据也显示,这3种杂波模型并不能很好地描述不同条件下的海杂波数据[6]。针对这一问题,文献[6]提出了使用广义逆高斯(Generalized Inverse Gaussian,GIG)分布来建模纹理分量,通过一定的参数变化可以得到广义逆高斯分布的3种极限分布:伽马分布、逆伽马分布和逆高斯分布。因此,当纹理分量建模为服从广义逆高斯分布的随机变量时,可以得到一种更为通用的杂波模型(Compound-Gaussian model with Generalized Inverse Gaussian texture,CG-GIG)。常用的海杂波幅度模型K分布、广义帕累托分布和CG-IG分布是CG-GIG分布的3种极限分布,所以CG-GIG分布的泛化能力更强,能够描述低、中、高分辨率的海杂波,这也是K分布、广义帕累托分布和CG-IG分布所不具备的。实测数据也显示,使用广义逆高斯分布来建模纹理分量可以更好地描述实测海杂波数据[6]。
根据上文的描述,CG-GIG模型可以对海杂波进行更为准确的建模。接下来的问题就是如何设计匹配CG-GIG模型的自适应检测器。在高斯模型下,Kelly根据广义似然比准则设计了广义似然比(Generalized Likelihood RaTio,GLRT)检测器[7]。但是GLRT检测器的计算量较大。在文献[8]中,根据两步法,首先假设协方差矩阵已知设计检测器,然后使用参考单元数据估计协方差矩阵,并将估计值代入到检测器中,得到了自适应匹配滤波(Adaptive Matched Filtering,AMF)检测器。在复合高斯模型下,CONTE提出了一种归一化匹配滤波(Normalized Matched Filtering,NMF)检测器,在杂波拖尾很重或者积累脉冲数很大时,NMF的检测性能趋近于最优[9]。NMF检测器并不依赖于纹理的先验分布,所以在不同的纹理下,NMF检测器会出现一定程度的性能损失。复合高斯杂波背景下的最优检测器的结构为匹配滤波器的输出与一个依赖数据项的门限相比[10]。CG-GIG杂波背景下的最优检测器为GLRT-GIG检测器[11],根据RMB准则,当积累脉冲数为N时,只有当参考单元数目大于2N时,检测器才能有较好的检测性能[12]。但是在实际的环境中,由于异常数据以及海尖峰等因素的影响,可选取的参考单元数目往往较少[13]。针对这一问题,学者们普遍将先验知识融入到检测器的设计中去,减少检测器的检测性能对于参考单元数目的依赖。例如当相干脉冲串具有对称间隔时,协方差矩阵具有双重对称性,即关于主对角线对称的Hermitian结构和次对角线对称的斜对称结构[14]。传统的协方差矩阵估计方法往往只用到了协方差矩阵的Hermitian结构。文献[15]研究了均匀高斯杂波背景下的斜对称检测器,并且推导了检测概率与虚警概率的数学表达式。文献[16]研究了在均匀和部分均匀高斯杂波背景下基于协方差矩阵斜对称结构的子空间目标检测问题。文献[17]研究了在K分布杂波背景下的斜对称检测器。除了斜对称结构外,协方差矩阵的Toeplitz结构以及圆结构也经常被用到检测器设计中[18]。除了利用协方差矩阵的先验结构外,还可以将散斑协方差视为一个随机变量,从而利用贝叶斯框架设计检测器。文献[19]指出,复高斯随机向量协方差矩阵逆的共轭先验分布为逆复Wishart分布。为了在数学上易于处理,通常将散斑协方差矩阵建模为一个服从逆复Wishart分布的随机矩阵,它包含自由度和均值矩阵两个参数,自由度用于衡量随机矩阵与均值矩阵之间的距离,自由度越大,距离越小。文献[20]设计了非均匀K分布杂波背景下利用散斑协方差矩阵先验分布的自适应检测器。文献[21]中,作者设计了在多输入多输出雷达背景下利用散斑协方差矩阵先验分布的自适应检测器。文献[22]中,在逆高斯纹理下,通过迭代估计自由度与纹理分量,设计了一种不依赖辅助数据的贝叶斯检测器。以上利用协方差矩阵先验知识的自适应检测器在参考单元数目较少的情况下,均具有令人满意的检测性能。除此之外,自回归(Auto Regressive,AR)模型[23-24]等参数模型也经常被当作先验信息用于检测器的设计。这些先验信息的使用能够大大地降低自适应检测器对于参考单元数目的依赖,从而提升检测器的检测性能。除了使用先验信息外,近年来一些基于数据降维的检测方法也被广泛研究,其好处在于不依赖任何的先验信息,通过对数据进行转换,大大减少了所需要估计的未知参数,并且在参考单元数目小于脉冲数时也具有不错的检测性能[25-27]。
根据贝叶斯框架,笔者在CG-GIG杂波背景下设计了两种自适应检测器。将散斑协方差矩阵建模为服从逆复Wishart分布的随机矩阵,首先根据广义似然比准则,通过待检测单元数据来估计自由度与杂波的纹理分量,设计了一个不依赖于辅助数据的贝叶斯检测器;然后根据最大后验准则,通过最大似然估计得到纹理分量的估计值,使用辅助数据与先验知识联合估计散斑协方差矩阵,得到了一个依赖于辅助数据与先验知识的贝叶斯检测器。实验结果表明,所提出的两种检测器在参考单元数目较少时,性能均优于已存在的检测器,在不同的参考单元数目下,所提出的依赖于辅助数据与先验知识的贝叶斯检测器始终具有最优的检测性能。
1 问题描述
1.1 检测问题描述
假设雷达在慢时间维积累了N个脉冲,则待检测单元的信号可以用一个N维的复向量z=[z(1),z(2),…,z(N)]T表示,检测问题可以描述为一个二元假设检验问题[22]:
(1)
其中,H0表示目标不存在的假设;H1表示目标存在的假设;α为目标的复幅度;p=[1,exp(j2πfd),…,exp(j2π(N-1)fd]T,表示目标的导向矢量,fd为目标的归一化多普勒频率;zk表示不包含目标信号的参考单元数据;L为参考单元的数目;c和ck为杂波向量。
1.2 信号模型介绍
在一个相干处理间隔(Coherent Processing Interval,CPI)内,纹理分量可以视为一个随机常数,此时复合高斯模型退化为球不变随机向量模型。杂波向量c和ck,k=1,2,…,L,可以使用一个正的随机变量τ(τk)和一个N维零均值复高斯向量u(uk)的乘积表示,数学公式描述如下:
(2)
其中,u表示散斑分量,是一个均值为0的复高斯向量,其协方差R=E(uuH);τ表示纹理分量。这里使用广义逆高斯分布对纹理分量进行建模,能够包含常用的伽马分布、逆伽马分布以及逆高斯分布,能更好地拟合实测杂波数据。广义逆高斯分布的概率密度函数为
(3)
其中,Kp(·)表示p阶第二类修正贝塞尔函数。令λ=(ab)1/2,μ=(b/a)1/2,这里μ被称作尺度参数。
在文中,将散斑协方差矩阵建模为一个服从复逆Wishart分布的一个随机矩阵,其概率密度函数为
(4)
其中,Σ是一个正定的均值矩阵;Γ(·)是伽玛函数;v表示自由度,自由度越大,R离均值矩阵Σ的距离越近。通常情况下v是未知的,所以在这里v被建模为一个均匀离散随机变量[28]。
根据对信号模型和杂波模型的分析,可以得到在H0假设和H1假设下,z的条件概率密度函数为
(5)
1.3 散斑协方差矩阵估计方法
在实际情况中,散斑的协方差矩阵通常是未知的,需要从参考单元的数据中进行估计。常用的散斑协方差矩阵估计方法为归一化采样协方差矩阵估计器(Normalized Sample Covariance Matrix Estimator,NSCME),可表示为[29]
(6)
NSCME对每个距离单元进行了功率归一化。当ANMF检测器使用NSCME后,具有对纹理的CFAR特性,但是无法保证对于协方差矩阵结构的CFAR特性。约束渐进最大似然估计器(Constrained Approximate Maximum LikeIihood Estimator,CAMLE)是通过平衡计算复杂度和估计性能提出的迭代估计器,可以保证自适应相干检测器对杂波纹理和散斑协方差矩阵的CFAR特性,可以表示为[30]:
(7)

2 贝叶斯检测器设计
2.1 不依赖辅助数据的贝叶斯检测器
本节设计的贝叶斯检测器对散斑协方差矩阵R进行积分,所以并不依赖于辅助数据,使用未知参数α的最大似然估计值、τ的最大后验估计值以及v的最小均方误差估计值来代替其真实值。检测器设计准则如下:
(8)
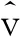
在H1假设下:
(9)
在H0假设下:
(10)
目标复幅度α的最大似然估计,可以通过最大化式(9)得到,也相当于最小化下式,即
L(α)=(z-αp)HΣ-1(z-αp)。
(11)
令式(11)对α求偏导,并令导数为0,可以得到α的最大似然估计为
(12)
前面介绍到,v被建模为一定区间上的均匀离散随机变量。其MMSE估计通过求其条件后验期望得到,根据贝叶斯公式,v的条件后验分布为
(13)
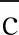
(14)
其中,
(15)
综上,检测判决式(8)可以化简为
(16)
下面计算在H1假设下,τ的MAPE。观察式(16)的分子,将含有τ的项提出,可以得到:
(17)
对式(17)取对数,然后对τ求偏导,令导数为0,化简可以得到:
(18)
其中,
(19)
根据笛卡尔符号准则,方程式(18)有惟一正根,并且一元三次方程有解析解。同理,在H0假设下有方程:
(20)
其中,
(21)

(22)
其中,ξ′是修正检测门限。
2.2 依赖于辅助数据的贝叶斯检测器
在上一小节中,因为对散斑协方差矩阵进行了积分,所以设计的检测器虽然能够使用协方差矩阵的先验分布信息,但是没有办法使用参考单元的信息。为了能够同时使用先验信息与参考单元的信息,这里设计了一种同时利用先验分布信息与参考单元信息的贝叶斯检测器。
根据最大后验广义似然比准则,检测判决式可表示为
(23)
目标复幅度α的最大似然估计为
(24)
使用两步法,首先假设R已知,然后再将R用其估计值代替,就得到了自适应检测器。
在H1假设下,计算τ的MAPE。在式(23)的分子中,提出与τ有关的项可得到:
(25)

(26)
对式(25)取对数,然后对τ求偏导,并令导数为0,解得τ的MAPE为
(27)
同理在H0假设下,τ的MAPE为
(28)
其中,q0=zHR-1z。
将式(24)、(27)、(28)代入式(23),就可以得到非完全自适应的检测器:
(29)
下面融合参考单元与先验分布信息来估计散斑协方差矩阵,从而得到完全自适应的检测器。与2.1节类似,在第k个参考单元,自由度v的条件后验密度函数为
(30)
在第k个参考单元上,自由度v的MMSE为
(31)
其中,
(32)

(33)

(34)
将式(31)、(34)代入式(33),然后取对数,并对散斑协方差矩阵R求偏导,可以得到
(35)
根据矩阵求导法则,可以得到
(36)
(37)
将式(36)、(37)代入式(35)中,并令结果为0,经过化简得到
(38)
式(38)可以写为
(39)
其中,
(40)

(41)

3 性能评估
3.1 BGLRT-GIG检测器的性能评估
首先使用仿真数据来评估BGLRT-GIG检测器的性能,将文中所提出的BGLRT-GIG检测器与GLRT-GIG检测器[11]和GLRT-R检测器[20]进行对比,均值矩阵Σ建模为具有一阶迟滞相关系数ρ的指数相关型协方差矩阵,Σi,j=ρ|i-j|,1≤i,j≤N。对于海杂波ρ∈[0.90,0.99],这里ρ=0.95,杂波参数设置为λ=5,p=2,u=Kp(λ)/Kp+1(λ),目标的归一化多普勒频率假设已知,且fd=0.2,自由度参数v的上下界分别设置为vl=N+1 和vu=3N,虚警概率设置为Pfa=10-3,检测门限通过n次独立的蒙特卡罗实验得到。其中n=100/Pfa,信杂比(SCR)定义为
(42)
其中,P=μKp+1(λ)/Kp(λ),为杂波的平均功率。
图 1展示了不同参考单元数目下,GLRT-GIG、BGLRT-GIG和GLRT-R检测器的性能曲线。从图中可以看出,BGLRT-GIG的检测性能优于GLRT-R的检测性能,这是因为GLRT-R检测器并没有考虑纹理的先验分布。当参考单元数目较小时,GLRT-GIG检测器的性能损失较大,BGLRT-GIG检测器的性能优于GLRT-GIG检测器的性能,这是因为参考单元数目随着参考单元数目的增大,GLRT-GIG检测器的性能会优于BGLRT-GIG检测器的性能。且随着参考单元数目的增加,散斑协方差矩阵的估计逐渐准确,此时只依赖协方差矩阵的先验信息是不够的,这也是文中设计依赖辅助数据的贝叶斯检测器的原因。

图1 不同参考单元数量L下的检测性能曲线图
图2展示了信杂比为-16 dB时,归一化多普勒频率对检测性能的影响。当目标落在主杂波区时,3种检测器都出现了一定程度的性能损失,随着目标距离杂波区越来越远,检测器的检测性能逐渐变好。从图2可以看出,当参考单元数目为14时,在不同的归一化多普勒频率下,文中提出的BGLRT-GIG检测器性能均优于GLRT-GIG检测器和GLRT-R检测器。
图2 信杂比为-16 dB和L=14时归一化多普勒频率和检测性能曲线图
图3展示了自由度对于BGLRT-GIG检测性能的影响。从图中可以看出,随着自由度的增大,检测性能也逐渐提升,这是因为自由度衡量的真实协方差矩阵与先验矩阵之间的距离,自由度越大,距离越近,先验矩阵也就更准确。

图3 不同自由度下检测性能曲线图
图4展示了虚警概率对检测器检测性能的影响。随着虚警概率的不断提高,两个检测器的检测性能逐渐变好,在不同的虚警概率下,笔者提出的BGLRT-GIG检测器均拥有最优的检测性能。

图4 不同虚警概率下L=14时的性能曲线图
接下来,使用南非实测海杂波数据评估两个检测器在不同参考单元数目条件下的检测性能。实验中采用TFC15-001数据集,该组数据集8 h的平均风速为8.14 m/s,8 h平均浪高为5.31 m,雷达的载频为 9 GHz,脉冲重复频率为5 kHz,距离分辨率为15 m。图5展示了不同杂波模型对于实测数据的拟合情况,参数估计方法使用文献[6]所提出的方法。从图中可以看出,采用广义逆高斯纹理建模的复合高斯模型能够很好地描述这组实测数据。
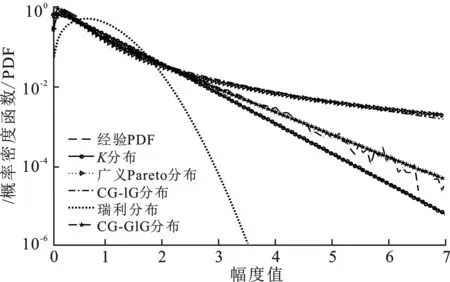
图5 TFC15_001数据幅度分布拟合图
在实测数据中,将第24个距离单元视为待检测单元,其余数据视为历史数据,使用NSCM估计器,每16个距离单元估计一次散斑协方差矩阵,最后取平均,当作先验矩阵。图 6展示了在实测数据中BGLRT-GIG检测器与GLRT-GIG检测器的检测概率曲线。从图中可以看出,当参考单元数目较少时,BGLRT-GIG检测器的性能较好,当参考单元数目比较充足时,GLRT-GIG检测器的性能更好。
3.2 BMAP-GIG检测器的性能评估
针对参考单元数目增多时,GLRT-GIG检测器优于文中提出的BGLRT-GIG检测器的问题,笔者又提出了一种依赖参考单元数据和协方差矩阵先验信息的BMAP-GIG检测器。本小节主要对BMAP-GIG检测器的性能进行评估,并将其与GLRT-GIG、BGLRT-GIG检测器进行对比。
首先使用仿真数据对BMAP-GIG检测器的性能进行评估,实验参数设置与上一小节相同。图7展示了在不同参考单元数目下,BGLRT-GIG、GLRT-GIG和BMAP-GIG检测器的性能曲线。

图7 不同参考单元数目的仿真数据的性能曲线图
从图7中可以看出,随着参考单元数目的增加,GLRT-GIG检测器的性能不断变好,最终优于BGLRT-GIG检测器。在不同的参考单元数目下,文中提出的BMAP-GIG检测器始终具有最优的检测性能。这是因为BGLRT-GIG检测器只使用了协方差矩阵的先验信息,GLRT-GIG检测器只使用了参考单元数据的信息,而BMAP-GIG检测器同时考虑了先验信息与参考单元数据的信息,所以在这3种检测器中,BMAP-GIG检测器拥有最优的检测性能。
下面使用南非实测海杂波数据对这3种检测器进行性能评估,使用的数据集为TFC15_001。在图 5中已经展示过广义逆高斯纹理建模的复合高斯模型对这组数据的拟合结果。 门限使用纯杂波数据进行计算。图 8展示了在实测数据中,不同参考单元数目下,3种检测器的性能曲线。从图中可以看出,当参考单元数目较少时,GLRT-GIG检测器的性能损失较大,性能最差。随着参考单元数目的增加,GLRT-GIG检测器的性能逐渐提升,最后会优于BGLRT-GIG检测器。在不同的参考单元数目下,BMAP-GIG检测器始终具有最优的检测性能。

图8 不同参考单元数目的实测海杂波加仿真目标的性能曲线图
由于BMAP-GIG检测器的判决式较为复杂,可使用蒙特卡罗实验的方法研究BMAP-GIG检测器的虚警性能。图 9分别展示了检测器门限对于归一化多普勒频率、杂波功率以及杂波一阶相关系数的CFAR特性。从图中可以看出,BMAP-GIG检测器的检测门限是近似独立于这3个参数的。由于BGLRT-GIG检测器中,需要进行迭代运算,所以相对于GLRT-GIG检测器计算复杂度较高;在BMAP-GIG检测器中,需要估计每个参考单元的自由度,并且还需要迭代估计协方差矩阵。所以在GLRT-GIG、BGLRT-GIG、BMAP-GIG检测器中,BMAP-GIG检测器计算复杂度最高,BGLRT-GIG检测器次之,GLRT-GIG检测器计算复杂度最低。
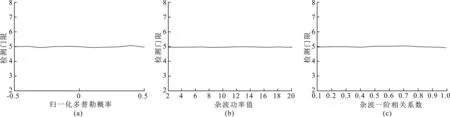
图9 BMAP-GIG检测器的虚警性能
4 结束语
笔者针对参考单元数目较少时,传统自适应检测器性能损失较大的问题,在CG-GIG杂波背景下,根据贝叶斯准则,通过将散斑协方差矩阵建模为服从复逆Wishart分布的随机矩阵,提出了两种贝叶斯检测器。其中BGLRT-GIG检测器不依赖于参考单元信息,BMAP-GIG检测器同时使用了先验信息与参考单元的信息。仿真数据实验和实测数据实验的结果表明,当参考单元数目较少时,BGLRT-GIG具有较好的检测性能,并且优于GLRT-GIG检测器。由于BMAP-GIG检测器同时使用了先验信息与参考单元的信息,所以在不同的参考单元数目下,BMAP-GIG检测器的性能均优于BGLRT-GIG和GLRT-GIG检测器。
