530 t特大型真空钢锭凝固过程热传递特性研究

吴穷

(二重(德阳)重型装备有限公司，四川618000)

关于钢锭凝固时间的计算，直接使用解析法计算非常困难，大部分研究者均通过简化至半无限大平板一维传热或者仿真模拟的方法研究[1-2]，特别是对特大型钢锭，基于现场的研究资料很少，不同的生产现场，钢锭传热条件各有差异。通过实际测量特定条件下的钢锭凝固过程参数，利用热平衡的方法，分析凝固的关键局部情况，简化计算，可以研究其凝固过程中的特性。

1 530 t特大型钢锭散热条件测量

以我公司530 t特大型真空钢锭为研究对象，如图1所示。对于锻造钢锭，必须确保锭身完全凝固，保温帽下部、锭身上部应为重点研究部位。利用手提测温枪测量记录图1中1～4点温度变化。钢锭以及钢锭模的相关参数见表1。

表1 钢锭以及钢锭模的相关参数Table 1 Related parameters of ingot and ingot mold

钢锭模外壁1～3点温度变化如图2所示。可以看出，钢锭模外壁温度在浇注完5 h内迅速升高，在20～30 h达到最大值，然后缓慢下降至较稳定温度。所以可以大致将钢锭凝固传热分为两个阶段：0～5 h为不稳定传热阶段；5～90 h为亚稳定传热阶段。

图1 530 t特大型真空钢锭凝固示意图Figure 1 Schematic diagram of solidification of 530 t super large vacuum ingot

图2 钢锭模外表面稳定变化趋势图Figure 2 The stable change trend diagram of the outer surface of the ingot mold

2 模型建立与计算

2.1 基于热平衡的凝固时间计算模型

根据热量平衡，有如下关系：

{钢水显热}+{凝固潜热}+{钢锭冷却显热}={钢锭模蓄热}+{钢锭模表面散热}

为简化求解过程，做如下假设：

(1)以点2位置的一段作为研究对象；

(2)该段在高度方向上热量的流进与流出相等，即该段散热只沿径向方向；

(3)钢锭模的蓄热过程仅在不稳定传热阶段；

(4)钢锭在凝固后温度降低散热量近似与钢锭模蓄热及不稳定传热阶段的散热相等；

(5)钢锭凝固后与钢锭模形成气隙，空气热传导远小于辐射传热，所以钢锭外表面与钢锭模内表面传热以辐射为主。

于是简化后热平衡关系如式(1)、(2)。其中计算所需要的相关参数见表2。

Q=E1+E2

(1)

2πr1hqt=πr22hρ1[L+cp(T0-Tf)]

(2)

式中，Q为总散热量；E1、E2分别为凝固显热和凝固潜热；r1、r2分别为钢锭模和钢锭半径，m；q为钢锭模散热的热流密度，包含辐射散热和对流散热，W/(m2·K)；ρ1为钢水密度，kg/m3；L为凝固潜热，J/kg；cp为钢水比热容，J/(kg·K)；T0、Tf分别为钢水初始温度和凝固温度，K。

表2 计算所需相关物性参数[3]Table 2 The required physical parameters for calculation

根据式(2)，可得出亚稳定传热阶段时间：

(3)

观察式(3)，可以发现当钢锭模和钢锭尺寸、浇注温度等确定以后，仅需求出变量q，即能计算出凝固过程亚稳定传热阶段所需时间。

2.2 钢锭模散热密度q的计算

钢锭模表面散热包括辐射散热和对流散热。

2.2.1 辐射散热

根据史蒂芬-玻尔兹曼定律，辐射散热的热流密度有：

qr=∅εσ[(T2/100)4-(T4/100)4]

(4)

式中，∅为形状角系数，钢锭被真空坑包围，可近似取值为1；ε为黑度值，一般氧化的钢或铁为0.8；σ为黑体辐射系数，5.67 W/(m2·K4)

钢锭模表面点2和真空坑壁点4的温度变化如图3所示。取平均值T2=380℃=653 K，T4=210℃=483 K，代入公式(4)，计算可得：

qr≈5778 W/m2

图3 钢锭模表面点2和真空坑壁点4的温度变化Figure 3 Temperature changes at point No.2 on the surface of the ingot mold and point No.4 on the vacuum pit wall

2.2.2 对流散热

对于钢锭模和真空坑之间的空隙，存在空气自然对流散热。而底部封闭的圆形夹层空气自然对流计算比较复杂，只能根据空气夹层自然对流传热的实验关联式[4]，求解努塞尔准数Nu，如式(5)所示，进而求得热交换系数h，估算得到qc。

(5)

Nu=hLc/k

qc=h(T2-T4)

式中，qc为对流换热的热流密度；h为换热系数；Nu为努塞尔准数；k为对流边界层导热系数；Lc为对流特征尺寸；Gr为格拉晓夫准数；Pr为普朗特准数，H为夹层高度，B为夹层宽度。

qc≈500 W/m2

所以，钢锭模表面总散热热流密度为：

q=qr+qc≈6300 W/m2

2.3 凝固时间计算

将q代入式(3)，可以计算出亚稳态传热时间为：

t=2.65×105s≈73.6 h

所以凝固总时间ts为：

ts=73.6 h+5 h=78.6 h

2.4 钢锭径向温度分布计算

图4是钢锭径向示意图，钢锭模和钢锭半径为r1、r2，钢锭模外表面温度、内表面温度以及钢锭外表面温度分别为Ta、Tb、Tc。现通过测量已知，Ta≈380℃，求出热流密度q≈6300 W/m2。

图4 钢锭径向示意图Figure 4 Radial diagram of ingot

2.4.1 钢锭模内表面温度计算

当传热达到稳定或亚稳定时，可以认为钢锭模没有热量积累，即：

(6)

根据傅里叶方程，有

(7)

又有A=2πrh，代入上式，并分离变量积分[3]，可得：

(8)

(9)

又有Q=2πr1hq，代入上式，有：

(10)

式中，k为钢锭模导热系数，取37 W/(m·K)，计算得到钢锭模内表面温度为：Tb≈790K=517℃。

2.4.2 钢锭表面温度计算

钢锭外表面与钢锭模外表面之间存在收缩气隙，所以钢锭表面与钢锭模内表面并非直接接触，由辐射和空气热传导综合传热，而空气的热传导可以忽略，仅考虑辐射传热，于是有：

q=∅εσ[(Tc/100)4-(Tb/100)4]

(11)

将Tb=790 K代入上式，求得Tc≈853 K=580℃。

2.4.3 钢锭径向温度分布

钢锭径向温度的求解是比较困难的，因为钢锭凝固潜热很大，虽然温度下降到凝固点温度，但随着潜热的释放，温度将保持在凝固点附近而不是立即下降；同时钢锭温度不同，其导热系数也不同，所以未完全凝固时其温度分布是很难计算的，下面仅求解完全凝固后的温度分布。

根据式(10)推导，有：

(12)

式中，Tx是不同半径处的温度；k为钢锭的导热系数，取30 W/(m·K)。

计算结果如图5所示。从图中可以看出，当rx≤0.1 m时，即温度约为1300℃时，钢锭芯部已经完全凝固。

图5 钢锭径向温度分布Figure 5 Radial temperature distribution of ingot

3 分析与讨论

3.1 钢锭模表面散热的热流密度

在上述计算与推导过程中，钢锭模表面散热的热流密度q是一个及其重要的参数，其准确性会影响所有计算的准确性，所以必须验证热流密度q是否准确。

图6 530 t钢锭脱模照片Figure 6 Photos of 530 t ingot demoulding

根据计算，钢锭外表面的温度Tc=580℃，可以在钢锭脱模后测量其表面温度进行验证。530 t钢锭脱模的照片如图6所示，钢锭锭身上部(椭圆框线内)实测温度约为570～580℃，与计算值相符，所以热流密度q值是比较准确的。

3.2 钢锭模蓄热

在简化计算模型时，认为钢锭凝固后温度降低所释放的热量与钢锭模蓄热及不稳定传热阶段散热相等。若假设不成立，将导致凝固时间计算产生较大误差。

钢锭凝固后温度降低所释放的热量Qi与钢锭模蓄热Qm计算分别如下：

Qi=πr22hρcpΔTi

(13)

Qm=π(r12-r22)hρcpΔTm

(14)

式中，ΔTi为钢水凝固温度与脱模后平均温度之差，ΔTm为钢锭模使用前后的温度差。

取钢锭的平均温度为1000℃，钢锭模平均温度450℃，其他物性参数参考表2，可得：

Qi=1.36Qm

另有不稳定传热阶段5 h散热量，所以钢锭温度降低所释放的热量基本与钢锭模蓄热及不稳定传热阶段散热相当。

3.3 钢锭与钢锭模之间气隙的热传导

在计算模型简化时，认为钢锭与钢锭模之间只存在辐射传热，而忽略气隙的导热。设空气热传导和辐射的等效换热系数分别为hc、hr，于是有

q=(hc+hr)(Tc-Tb)

(15)

按一般凝固收缩率3%计算，气隙厚度δ1≈50 mm，空气在500～600℃时的导热系数k约为0.07 W/(m·K)，于是空气热传导的等效换热系数为：

而热辐射的等效换热系数[4]为：

hr=εC(Tc2+Tb2)(Tc+Tb)≈100 W/(m2·K)

由此可见完全可以忽略空气气隙的导热。

3.4 凝固时间的影响因素

改写式(3)，得到下式：

(16)

式中，β是钢水释放热量与散热的比值。

从式中可以看出，凝固时间与散热条件q、钢锭半径r2、钢锭模半径r1相关性较大。只需要实际测得不同情况下的散热条件，即可计算得到凝固时间。

关于凝固层厚度与时间的关系，有著名的Chvorinov公式，明确指出凝固层厚度与凝固时间呈平方根关系。

t=δ2/K2

(17)

式中，δ为凝固层厚度，cm；K为凝固系数，铸钢在金属型中凝固，K=2.7～3[6]。

可以发现本文凝固时间计算公式与Chvorinov公式具有相同的形式。图7是Chvorinov公式、日本JSW、二重(EZ)的数据以及本文凝固时间计算值之间的比较，可以看出，半径为2000 mm的钢锭凝固时间的偏差在5 h以内，也验证了本文凝固模型计算的准确性。

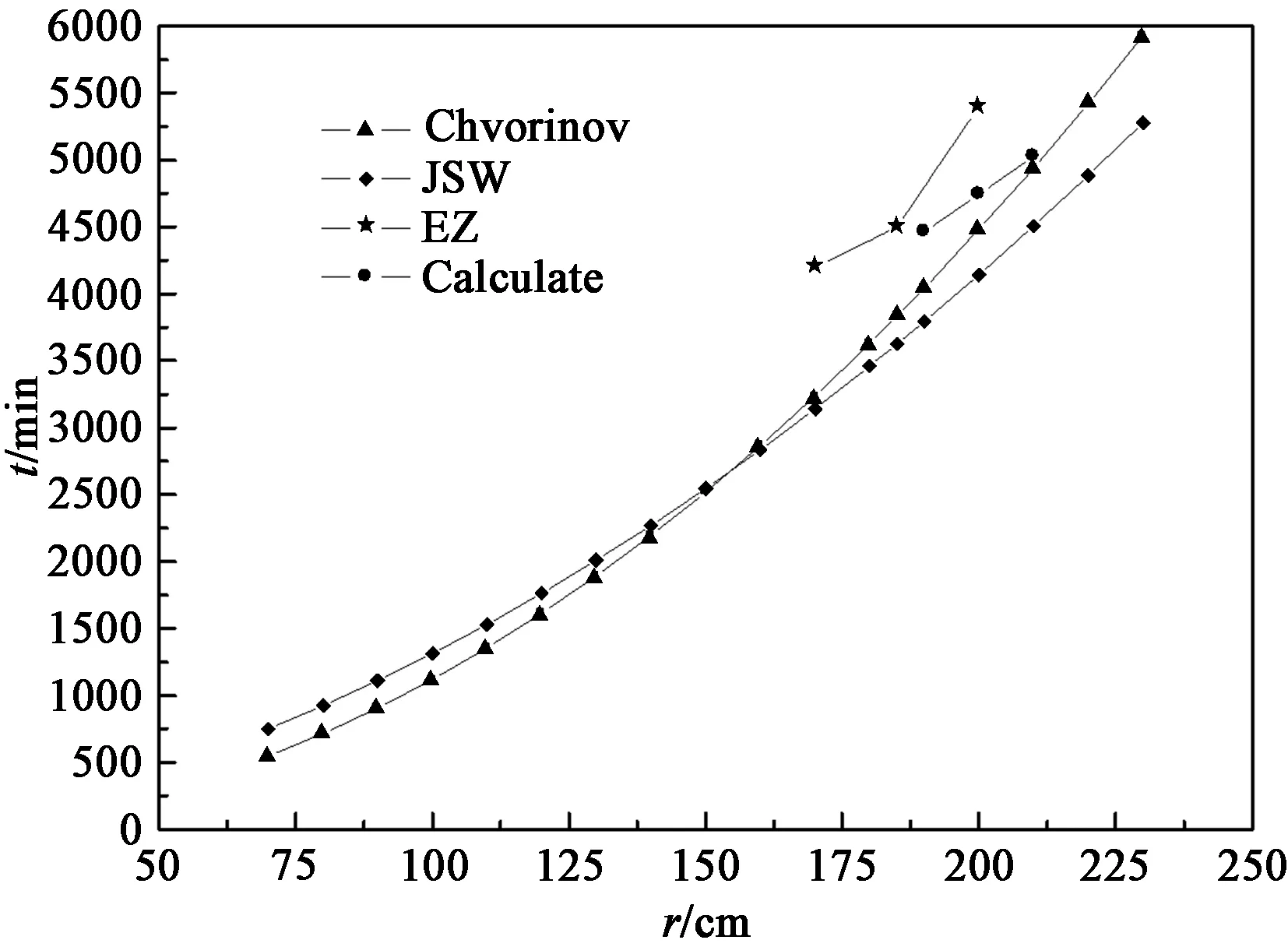
图7 凝固时间计算值比较Figure 7 Comparison of calculated values of solidification time

4 结论

(1)通过现场测量，利用热平衡法计算了530 t特大型真空钢锭的凝固时间，总凝固时间为不稳定传热时间和亚稳定传热时间之和，约为78.6 h，与经验公式和现场脱模时间相近。

(2)利用稳定传热的方法，计算得到钢锭凝固后的表面温度与实际测量相吻合。还估算了钢锭截面径向温度分布，对钢锭内部温度有近似了解。

(3)对模型的假设条件进行了分析，该模型可以运用于其他大小的钢锭凝固时间的计算。