高速铁路线路条件对列车追踪间隔时间的影响分析
2021-04-29彭其渊
李 栋,彭其渊
(1.西南交通大学 交通运输与物流学院,四川 成都 611756;2.西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 611756)
0 引言
近年来,我国高速铁路干线运输供需矛盾逐渐凸显。列车追踪间隔时间直接影响发车频率,对其进行压缩能显著提高高速铁路的通过能力[1]。
相关学者分析高速铁路列车追踪间隔时间的计算因素,结合列控系统及CTC 的技术特点,给出高速铁路列车追踪间隔时间的计算方法[2],在此基础上研究了限速条件下的列车追踪间隔时间计算方法[3]。高速铁路列车追踪间隔时间的影响因素主要包括线路条件、咽喉区长度、咽喉区限速、动车组性能、闭塞分区长度及信号系统等[4-5]。
在我国中西部地区高速铁路的建设中,由于地形限制较大,越来越多的长大坡度线路投入使用,如西成客运专线(西安北—成都东)在秦岭地带设计了25‰的大坡度线路,并且长度累计达到46 km;建设中的郑万客运专线(郑州东—万州北)沿线共使用了12 个30‰的坡段,合计长度达到85.5 km。复杂的线路条件对列车的运行以及追踪间隔时间有明显的影响,对其进行研究具有理论和实际意义,张守帅等[6-7]研究了长大下坡对区间通过能力和追踪间隔时间的影响,但长大下坡只是线路条件对列车追踪间隔时间产生影响的情况之一,尚缺乏全面系统性的研究。文中将探讨线路条件的各方面对列车追踪间隔时间的影响,以期为列车追踪间隔时间的优化措施提供思路及研究基础,也为新线建设以及线路改造时对线路的设计提供参考。
1 列车追踪间隔时间计算及影响因素分析
在各类列车追踪间隔时间中,列车区间追踪间隔时间(I追)、列车出发追踪间隔时间(I发)以及列车到达追踪间隔时间(I到)是最典型也是较大的3 类,以这3 类追踪间隔时间为对象,在分析计算方法的基础上,找出相关影响因素。
1.1 列车追踪间隔时间计算方法
(1)高速铁路列车区间追踪间隔时间如图1 所示,I追的计算公式为
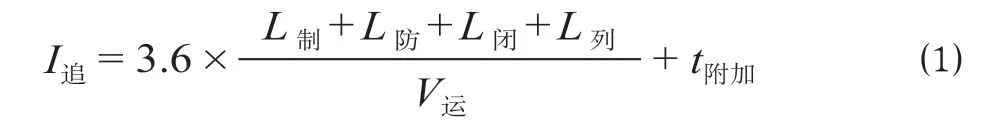
式中:L制为ATP 监控制动距离,m;L防为列车安全防护距离,m;L闭为闭塞分区长度,m;L列为列车长度,m;V运为列车区间运行速度,km/h;t附加为附加作业时间,s。
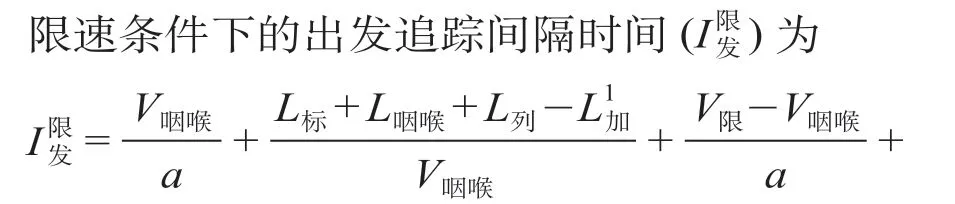
(2)高速铁路列车出发追踪间隔时间如图2 所示,I发的计算公式为

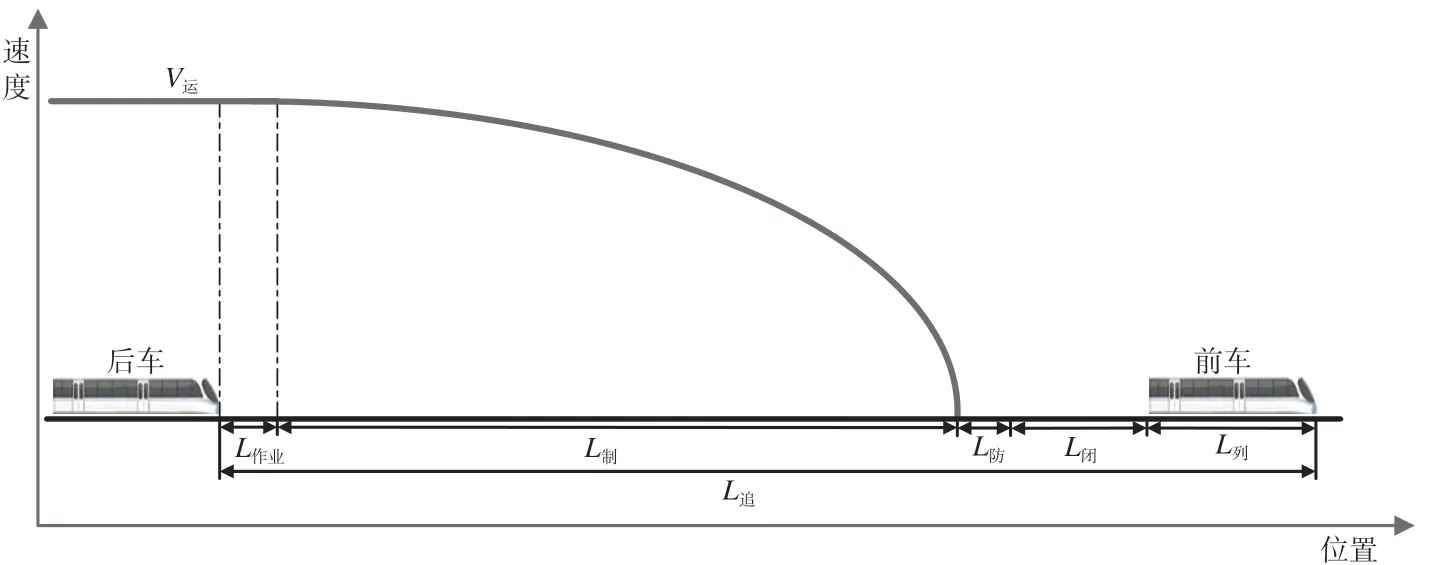
图1 高速铁路列车区间追踪间隔时间Fig.1 Train section tracking interval of high speed railway

图2 高速铁路列车出发追踪间隔时间Fig.2 Train departure interval of high speed railway
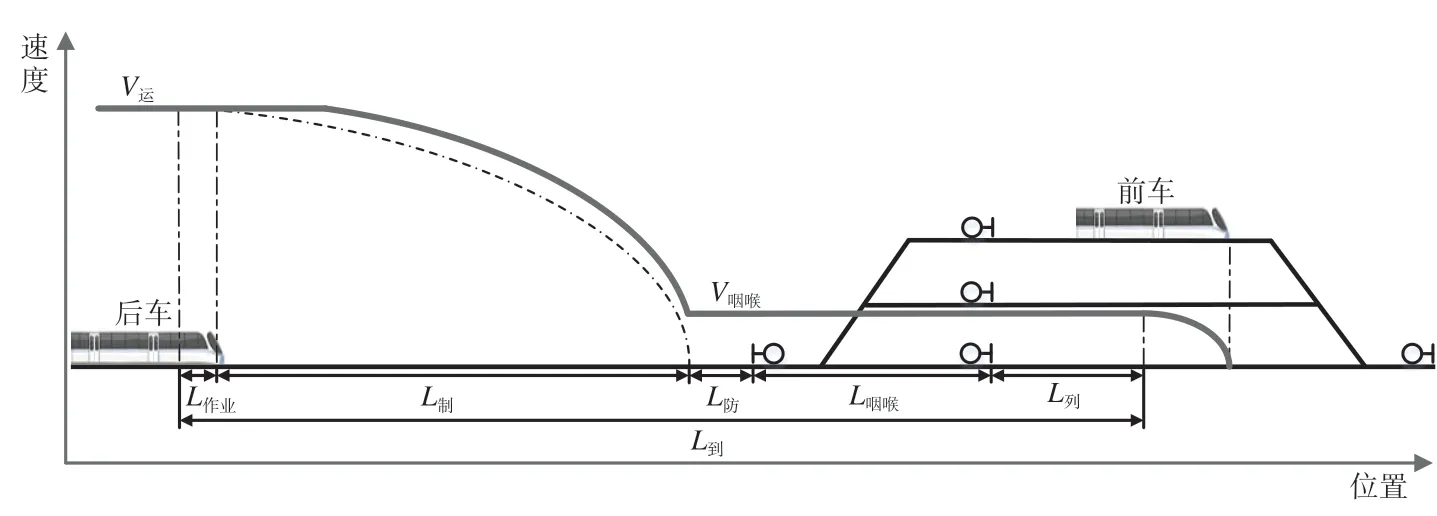
图3 高速铁路列车到达追踪间隔时间Fig.3 Train arrival interval of high speed railway

1.2 影响因素分析
由公式(1)—(3)可知,各类列车追踪间隔时间的影响因素包括L制,V出发,V到达,V运,L闭,L咽喉,咽喉区限速和各项作业时间,咽喉区长度及限速由站场配置确定,作业时间由列控系统确定,L制,V出发和V到达这些取值经牵引计算得到。
在牵引计算中,列车牵引力与制动力由动车组自身技术条件确定,坡道附加阻力与曲线附加阻力则由线路平、纵断面决定,不同平、纵断面产生不同的附加阻力,使得列车加速度发生变化,进一步影响到牵引或制动的距离和时间,因而线路条件对列车追踪间隔时间会产生影响。
此外,由于受到地形限制等原因,存在不良线路区段(小半径曲线、桥隧等),导致列车经由时限速运行,如京沪高速铁路(北京南—上海虹桥)上海虹桥站至黄渡线路所区间存在2 500 m 的小半径曲线,列车限速180 km/h 运行,此时列车的运行过程发生了变化,在考虑附加阻力影响的基础上,还需要考虑限速运行的影响。
2 线路条件对列车追踪间隔时间影响分析
2.1 线路附加阻力的影响
2.1.1 坡道附加阻力影响分析
由《列车牵引计算规程》[8]可得单位坡道附加阻力wi与线路坡度i的关系为

不同的线路纵断面对应着线路的坡度不同,产生的坡道附加阻力不同。下坡道上产生的坡道附加阻力为负,相比平直道上,列车启动加速度增大,制动加速度减小,有利于列车启动,不利于列车制动,故下坡道上出发追踪间隔时间会减小,区间追踪间隔时间与到达追踪间隔时间会增大;上坡道上相反。坡道附加阻力的大小与坡度值的大小呈正相关。
2.1.2 曲线附加阻力影响分析
不同曲线半径R的曲线附加阻力wr不同,经验公式为

式中:600 为经验常数。
相比列车在直线线路上运行,列车在曲线线路上会受到额外的运行阻力,列车制动加速度增大,启动加速度减小,有利于列车制动,不利于列车启动,故出发追踪间隔时间会增大,区间追踪间隔时间与到达追踪间隔时间会减小。曲线附加阻力的大小与曲线半径呈负相关。
2.2 限速运行的影响
限速时列车的运行过程发生变化,列车追踪间隔时间的计算不能按照正常运行时的方法直接求解,需要进一步推导。为便于表述,推导公式中将变加速过程表达为匀变速运动形式。
2.2.1 限速下的区间追踪间隔时间
当存在限速区段时,前行列车的制动会迫使后行列车减速,为避免这种情况的发生,相邻追踪列车之间需要在正常追踪运行的基础上预留出额外的追踪距离,这就使得区间追踪间隔时间增大,增大的区间追踪间隔时间包括以下2 个部分[9]。


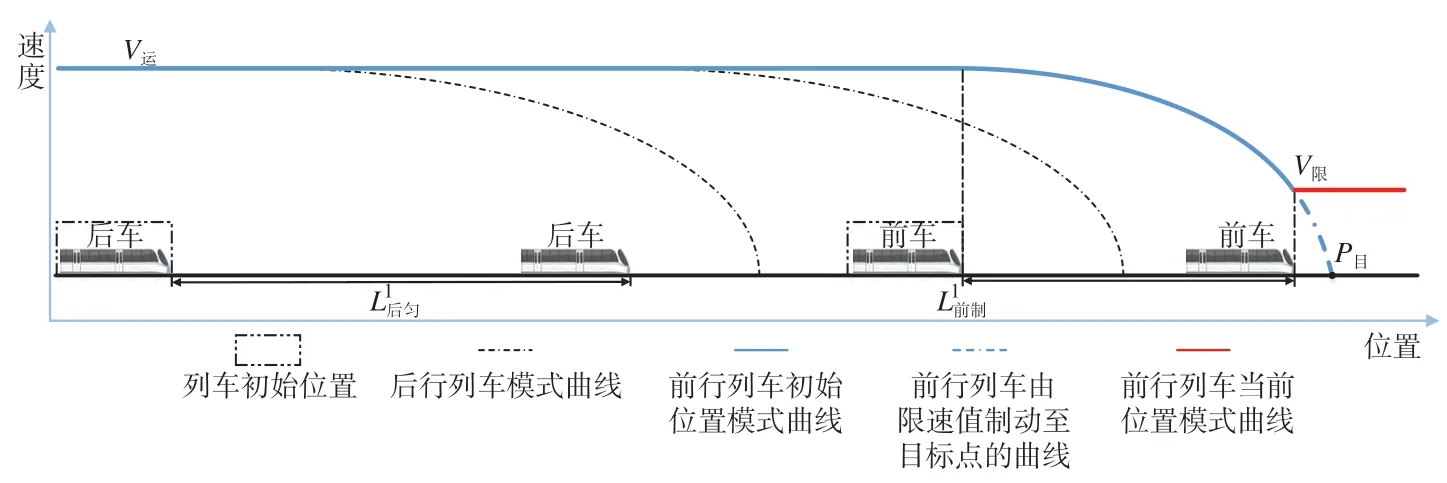
图4 限速条件下列车区间追踪间隔时间IFig.4 Train section interval under speed limit condition I
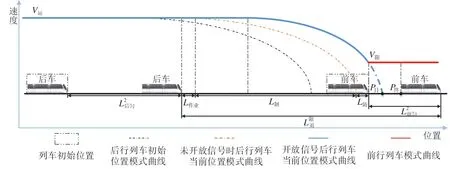
图5 限速条件下列车区间追踪间隔时间IIFig.5 Train section interval under speed limit condition II
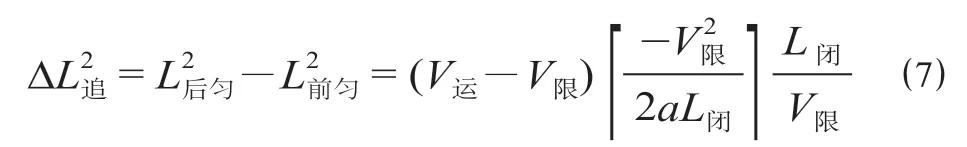


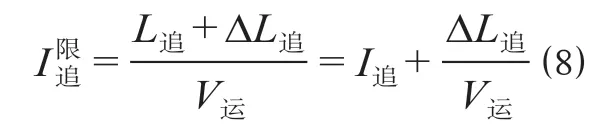
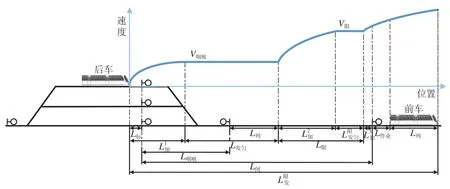
图6 限速条件下列车出发追踪间隔时间Fig.6 Train departure interval under speed limit condition
式中:L追为正常条件下的区间追踪间隔,m;I追为正常条件下的区间追踪间隔时间,s。


2.2.2 限速下的出发追踪间隔时间




2.2.3 限速下的到达追踪间隔时间
经研究相关文献,发现不同限速值下,到达追踪间隔时间需要分别讨论。王超宇[9]提出在列车限速进站过程中存在2 个速度临界值Vvalid和Vmax,两者分别为限速起点P限处所对应的列车正常运行时进站信号机开放前后模式曲线的速度值,易知,不同位置处的临界值不同。
(1)当V限>Vmax时,由于列车正常进站过程中在P限处的速度最高为Vmax,因而V限对列车运行不造成影响,到达追踪间隔时间不变。间得到压缩,并且随着V限的减小而减小。
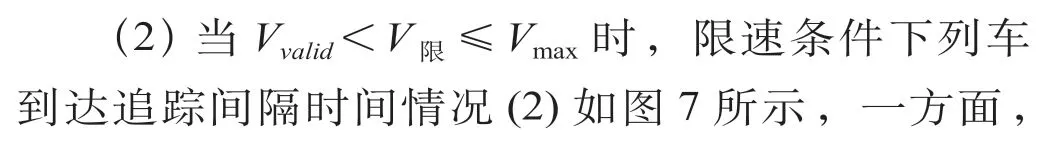


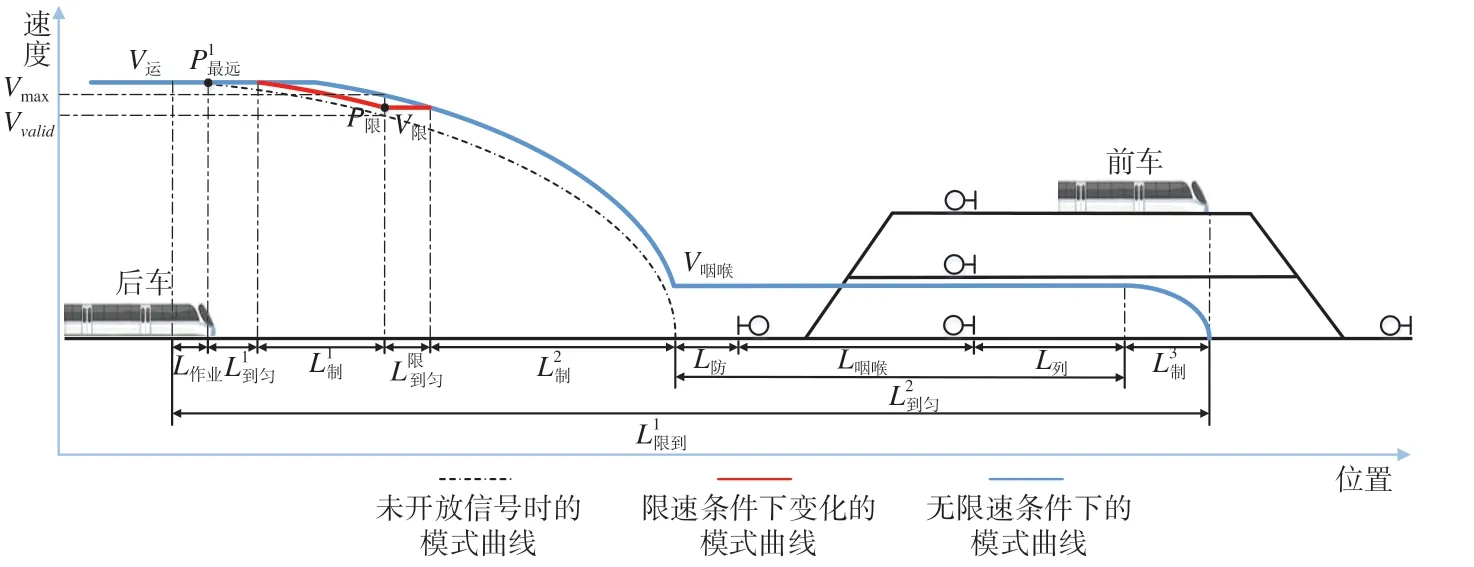
图7 限速条件下列车到达追踪间隔时间情况(2)Fig.7 Train arrival interval under speed limit condition (2)

综上所述,到达追踪间隔时间随着限速值的减小,先不变,再增大,然后减小。
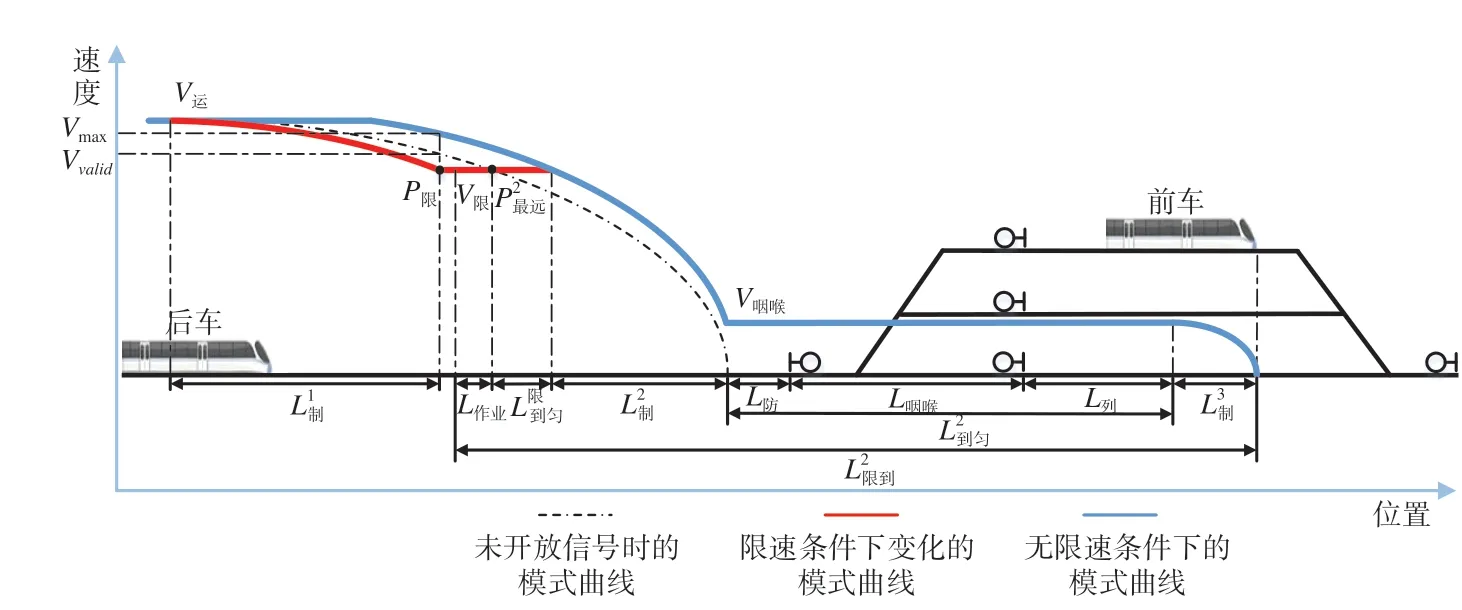
图8 限速条件下列车到达追踪间隔时间情况(3)Fig.8 Train arrival interval under speed limit condition (3)
3 检算结果及分析
为验证理论分析结果,构造理想化列车运行场景借助牵引计算软件对各类列车追踪间隔时间进行检算:①列车运行在长坡段或长曲线上;②仅考虑坡度、曲线或限速中的某一项对列车追踪间隔时间的影响。检算中的线路坡度与曲线半径的取值根据《高速铁路设计规范》确定[10]。
3.1 参数取值
选用CRH380BL 型动车组,采用16 辆编组,车长400 m,该动车组ATP 参数如表1 所示。
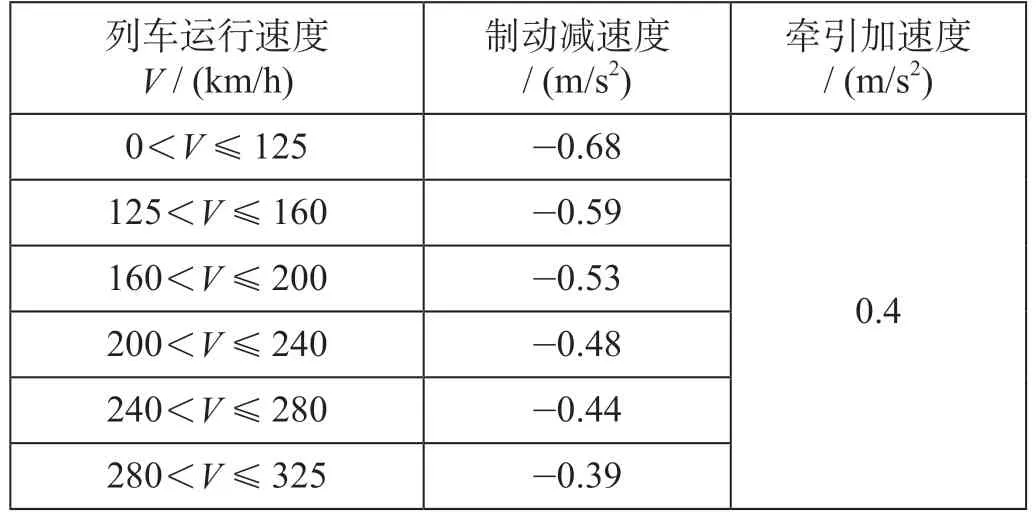
表1 CRH380BL 动车组ATP 参数Tab.1 CRH380BL EMU ATP parameters

3.2 不同线路附加阻力的检算结果及分析
3.2.1 不同坡度下区间追踪间隔时间的结果及分析
为验证线路坡度对I追的影响,设置了0‰ ~ 25‰的上下坡道,基于公式(1),利用牵引计算软件计算不同区间运行速度与不同坡度下的I追,将结果绘制得到不同坡度值下的列车区间追踪间隔时间如图9 所示。
由图9 可知,与平直道相比,不同坡度下区间追踪间隔时间的变化情况如下。
(1)I追在上坡道上会减小,并随坡度值的增大而减小,在下坡道上会增大,并随坡度值的增大而增大,且速度越高,不同线路坡度对应的I追之间的差距就越大。
(2)速度为300 km/h 时,25‰的下坡道使I追增加50 s 左右,25‰的上坡道使I追减小20 s 左右,可见下坡道对I追的影响程度比上坡道更大。
(3)在某一确定的线路坡度上,I追的变化不是单调的,而是随着运行速度的增加,I追先减小再增大。
3.2.2 不同坡度下出发追踪间隔时间的结果及分析
I发受站坪范围内线路坡度(主要是咽喉区坡度)与一离去范围内线路坡度的共同影响。设置一离去区间为0‰ ~ 25‰的上下坡道,咽喉区为0‰ ~ 6‰的上下坡道,基于公式(2),利用牵引计算软件计算每一坡度值下的I发,将结果绘制得到不同坡度下的列车出发追踪间隔时间如图10 所示。
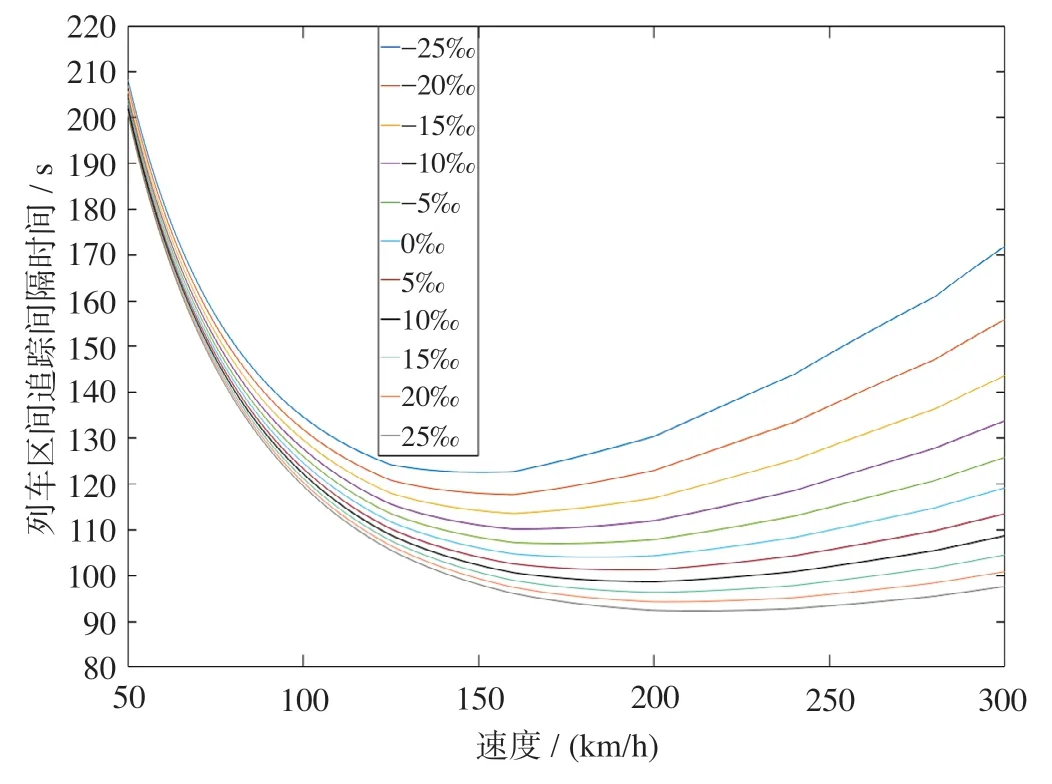
图9 不同坡度值下的列车区间追踪间隔时间Fig.9 Train section tracking interval under different slope values
由图10 可知,与平直道相比,不同坡度下出发追踪间隔时间的变化情况如下。
(1)I发在下坡道上较小,且坡度值越大,列车启动及出站过程就越快,I发越小;上坡道的影响情况相反。
(2)站坪坡度对I发的影响在8 s 左右,一离去坡度对I发的影响在12 s 左右,这是由于站坪范围内线路坡度较小,一离去范围内走行距离较短,I发所受影响均较小,线路条件不是I发的主要制约因素。
3.2.3 不同坡度下到达追踪间隔时间的结果及分析
与出发追踪间隔时间相同,到达追踪间隔时间受站外线路坡度及站坪范围内坡度的共同影响,但根据图10 结果,站坪坡度的影响不明显,故主要探讨站外线路坡度对I到的影响。同样设置0‰ ~ 25‰的上下坡道,基于公式(3)利用牵引计算软件计算并绘制得到不同坡度下的列车到达追踪间隔时间如图11 所示。
由图11 可知,与平直道相比,不同坡度下到达追踪间隔时间的变化情况如下。
(1)I到在上坡道上较小,并且坡度值越大,I到越小,下坡道上相反;速度越高,不同线路坡度对应的I到之间的差距就越大。
(2)速度为300 km/h 时,25‰的下坡道使I到增加75 s,25‰的上坡道使I到减小30 s 左右,下坡道对I到的影响程度较上坡道更大。
(3)I到随着速度的增加而增加,可考虑进站前减速以压缩I到。
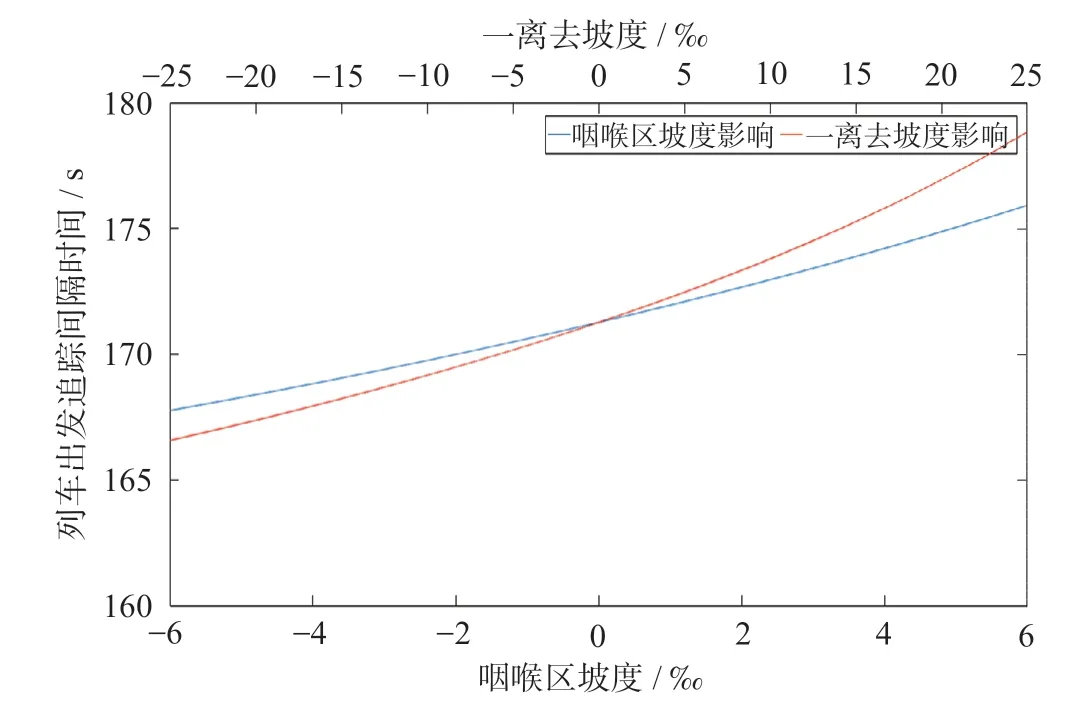
图10 不同坡度下的列车出发追踪间隔时间Fig.10 Train departure interval under different slope values
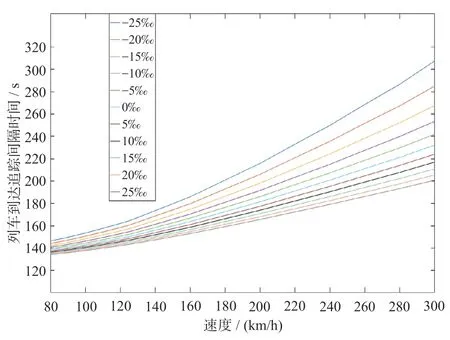
图11 不同坡度下的列车到达追踪间隔时间Fig.11 Train arrival interval under different slope values
3.2.4 不同曲线下列车追踪间隔时间的结果及分析
取区间运营速度为300 km/h,基于公式(1)—(3)利用牵引计算软件计算了平直道上和半径分别为5 000 m,7 000 m,9 000 m 的曲线上正常运行时不同曲线半径下的列车追踪间隔时间如表2 所示。

表2 正常运行时不同曲线半径下的列车追踪间隔时间Tab.2 Train tracking interval under different curve radii in normal operation
由表2 可知,正常运行时不同半径的曲线对各类列车追踪间隔时间基本无影响,原因是产生的曲线附加阻力较小。
3.3 限速运行下的检算结果及分析
3.3.1 限速下区间追踪间隔时间的结果及分析
由公式(8)—(9)可知,限速下的I追与限速值相关,为分析相关性,在区间运营速度为300 km/h,设置80 ~ 280 km/h 的限速值,利用牵引计算软件分别计算对应的I追并绘制得到不同限速值下的列车区间追踪间隔时间如图12 所示。为便于分析其突变性,同时计算了不同限速值下前车需出清的闭塞分区数量,即公式(9)中的
由图12 可知,限速条件下的区间追踪间隔时间随着限速值的减小,整体上呈现增大的趋势,但存在局部的突降。

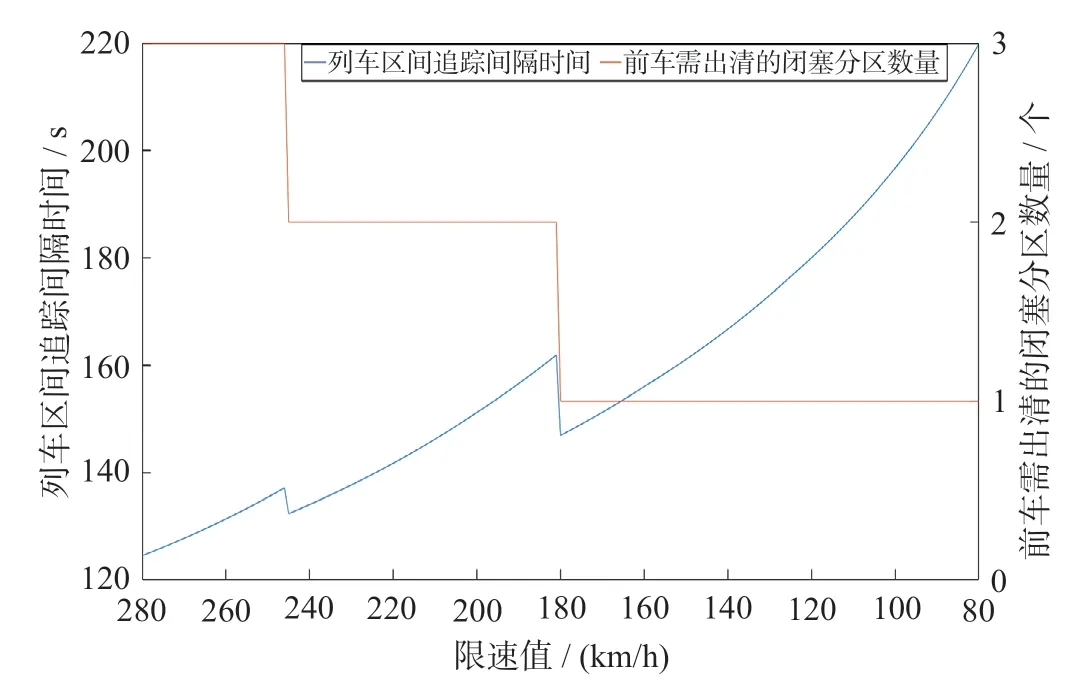
图12 不同限速值下的列车区间追踪间隔时间Fig.12 Train section tracking interval under different speed limits
3.3.2 限速下出发追踪间隔时间的结果及分析
经计算,正常运行时,V出清为139.5 km/h。存在限速时,I发受限速值以及限速区段长度的影响,分 别 设 置80 ~ 140 km/h 的 限 速 值 和500 ~ 1 400 m的限速区段,基于公式(10)利用牵引计算软件计算并绘制得到不同限速条件下的列车出发追踪间隔时间如图13 所示。需要说明的是,在计算限速值对I发的影响时,将限速区段长度设为600 m,在计算限速区段长度对I发的影响时,将限速值设为110 km/h。
对于限速值,在一定范围内,出发追踪间隔时间随着限速值的增大而减小,但达到一临界值时,出发追踪间隔时间不再变化。临界值为满足公式(16)的限速值,即列车在限速区段内一直加速运行,此时限速区段的存在不制约出发追踪间隔时间。

随着限速区段的增长,出发追踪间隔时间先保持不变,后逐渐增大,变化的临界值同样是满足公式(16)的限速长度。限速区段短于临界值时,列车在其中一直加速运行,不受限制;当限速区段长于临界值时,列车先加速后匀速,速度受到限制,在其中运行时间增大,出发追踪间隔时间增加。
整体上看,限速区段越短,限速值越大,出发追踪间隔时间越小;限速值对I发的影响程度更大。
3.3.3 限速下到达追踪间隔时间的结果及分析
限速下的I到与限速值大小相关,设置80 ~ 300 km/h 的限速值,同时为验证在不同的限速位置是否具有相同的规律,分别设置了车站一、二、三接近区间内存在限速,基于公式(12)和(15)利用牵引计算软件计算并绘制得到不同限速条件下的列车到达追踪间隔时间如图14 所示。
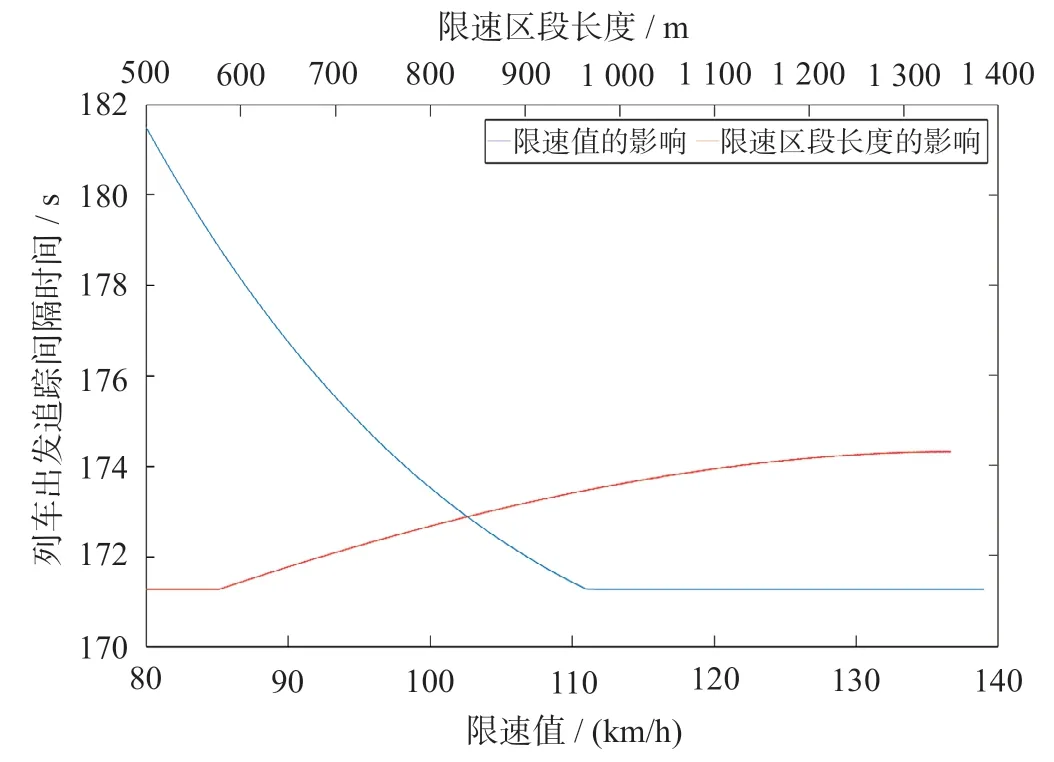
图13 不同限速条件下的列车出发追踪间隔时间Fig.13 Train departure interval under different speed limit conditions
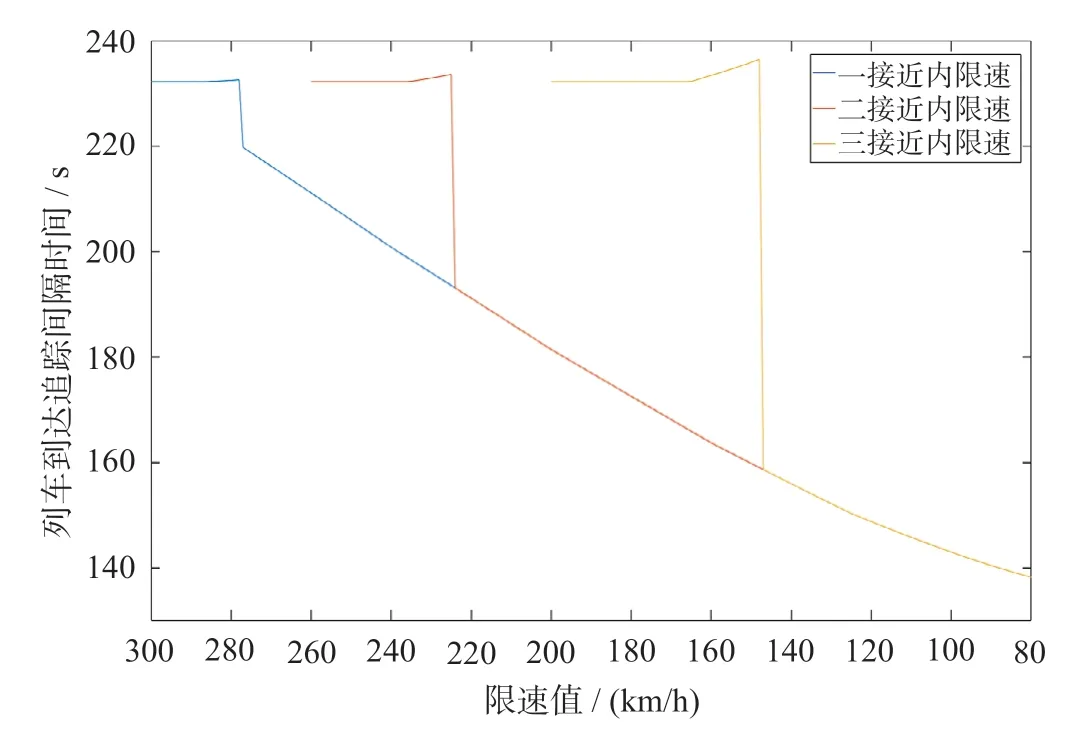
图14 不同限速条件下的列车到达追踪间隔时间Fig.14 Train arrival interval under different speed limit conditions
限速位置越接近车站,Vmax与Vvalid越小。3 处限速的结果曲线均满足规律:当V限> Vmax时,I到不受影响;当Vvalid< V限≤ Vmax时,I到会随限速值减小而微小增加;当V咽喉< V限≤ Vvalid时,I到发生突降,随限速值减小而减小,并且相比正常运行时减小,验证了理论分析的结果。
4 结论
列车追踪间隔时间是高速铁路通过能力的限制因素之一,对列车追踪间隔时间进行压缩的基础是研究其影响因素及影响机制。通过分析线路条件的影响机制,检算不同线路条件下的列车追踪间隔时间,对比分析与总结出线路条件对各类列车追踪间隔时间的影响规律。
(1)线路条件对列车追踪间隔时间产生影响的原因包括线路平、纵断面产生的附加阻力以及存在因线路条件导致限速运行2 方面。
(2)坡道附加阻力的影响为:相比平直道上运行,下坡道上,区间追踪间隔时间、到达追踪间隔时间增大,随坡度值的增大而增大,出发追踪间隔时间减小,随坡度值增大而减小;上坡道影响情况相反。由于列车实际受到的曲线附加阻力较小,各类列车追踪间隔时间基本不受影响。
(3)相比正常运行,限速运行时,区间追踪间隔时间随限速值的减小而增加,但存在局部的突降;出发追踪间隔时间增大,限速值越大、限速区段越短,则增加越少;到达追踪间隔时间随限速值的减小,呈现先不变,后增大,再减小的规律。
