感知乘客心理的出租车动态合乘优化方法
2021-04-28薛守强宋瑞安久煜王攸妙
薛守强,宋瑞,安久煜,王攸妙
(北京交通大学,综合交通运输大数据应用技术交通运输行业重点实验室,北京100044)
0 引言
合乘问题(ride-sharing),也称共乘,即将原本空闲的车上座位利用起来,不仅合理利用路面车辆闲置运力资源,还可有效减少私家车出行,缓解城市交通压力,消减出行成本。
国内外专家学者都热衷于研究合乘问题。Hosni H.[1]提出一种混合整数规划模型并用拉格朗日分解展开求解;Alonso-Mora[2]等提出成对共享图理论及对应算法;之后Simonetto[3]等在文献[2]基础上通过改进策略,保证解结果的次优,使计算时间缩短为原先的1/4。但这类研究均假设乘客具有完全理性的出行行为,侧重于优化系统出行效率,忽视乘客在实际出行中具有有限理性行为的特征。
在挖掘乘客出行心理特征方面,Wang[4]等从感知价值和感知风险探讨非用户使用拼车服务的驱动因素;Nguyen-Phuoc[5]研究网约车乘客满意度和忠诚度的相关关系;张薇[6]从行程时间、费用、舒适度的角度判断乘客合乘决策。这类研究未能将乘客对服务的感知体验应用于微观匹配调度机制。
鉴于此,本文综合考虑乘客具有有限理性行为特征优化系统出行效率,通过多个方面动态感知乘客得失心理,并将其融入到合乘问题的匹配调度机制中。本文改进了文献[2-3]中的算法框架,令其不仅能够解决动态合乘——NP 难问题,而且通过捕捉乘客心理和实际车辆匹配情况制定匹配调度方案,从而真实地遵从乘客主观意愿,为乘客提供更为满意的出行体验。
1 问题描述
本文研究单对多的出租车动态合乘问题:即存在一组出租车队,乘客可随时向共乘系统提出出行需求。系统采用滚动更新机制,每隔周期时长t0收集乘客请求和当前车辆具体信息。在满足各约束下,系统以优化出行效率和提升感知价值为目的,为乘客匹配合适车辆,制定最优出行路线。未被分配到的乘客将进入下一周期重新优化,若至其最大等待时间仍未被安排车辆服务,将取消该订单。此外,一名乘客只能由一辆车服务,一个周期内一辆车最多接受一名乘客请求的要求。
数学定义在一个完全有向的G={ }V,A路网中,其中,V为所有站点集合,i,j为路网顶点,A表示(i,j)点间的路段集合,A={(i,j)|i,j∈V,i≠j} ,ti,j表示车辆在路段(i,j)间消耗的时间。请求集合R包含各乘客出行请求信息r={(pr,dr,rt,δ,η,d*r,wr)|r∈R} ,其中,包括乘客r的上车位置pr、下车位置dr、发出请求的时间rt、最大等待时间δ、最大绕行时间η、到达目的地最短用时,以及乘客r对时间、费用和共乘人数的权重大小wr=[w1,w2,w3] (详细见2.3 节)。C为车辆集合,同时每辆车c∈C的承载能力为Lc。
2 算法框架构建
定义可行出行对(c,r):车辆c在满足各约束下能够服务乘客r,则构成一个可行出行对(c,r)。每个(c,r)包含3 项信息{t,Ttime,t,Pvalue,t} ,其中,t为行程,指车辆c服务乘客r实际路径方案,Ttime,t,Pvalue,t分别为行程t中所有乘客的总损耗时间和总感知价值。
为解决一段时间内的出租车动态合乘问题,系统将该段时间按照t0分为 |M|个周期,从第1 个周期开始,进行滚动更新优化,具体流程如图1所示,虚线框内为第2节算法框架主要内容。
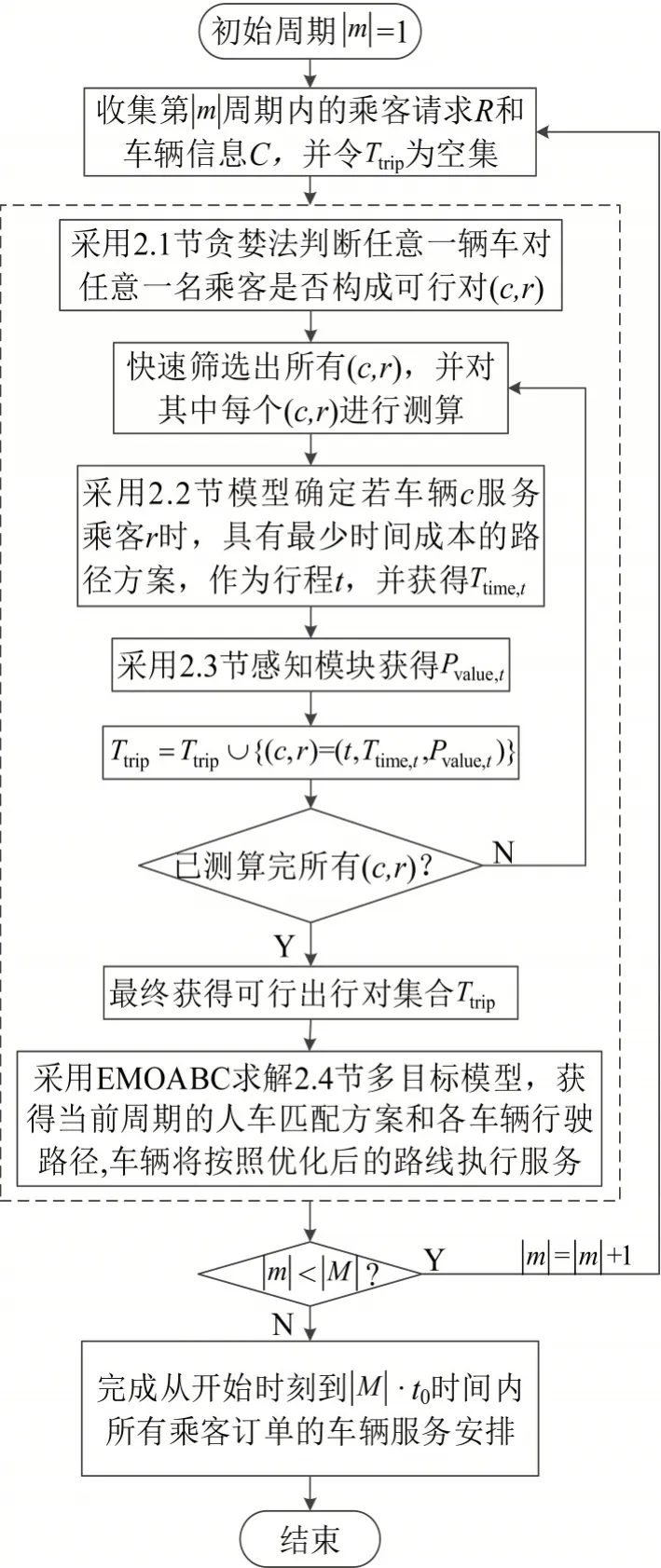
图1 算法流程图Fig.1 Algorithm flowchart
2.1 可行出行对
为获取∀c∈C与∀r∈R间所有可行匹配,采用贪婪法中插入法快速判断车辆c是否可服务乘客r。下面简要说明判断过程:若车辆1 当前服务路线是(d1,d3,d2),即乘客按照乘客1→乘客3→乘客2的顺序先后下车,则新乘客4的上、下车点p4,d4从开始位置依次尝试插入;若(p4,d4,d1,d3,d2)满足各约束要求,则贪婪法终止,表明车辆1 可服务乘客4,构成可行出行对,但车辆1 服务乘客4 的最优路线将由2.2 节模型求解;如不满足则依次改变插入位置如(p4,d1,d4,d3,d2)继续判断,若最后仍找不到满足约束的插入位置,则说明车辆1不能服务乘客4,贪婪法终止。
2.2 最优出行路径
经典拨号问题(Dial a Ride Problem,DARP)假设乘客均未上车,其上、下站点对称分布。但因滚动更新机制,部分乘客已在车中,故本节改进文献[7]中的3指标模型,确定(c,r)中车辆c的最优路径为,并令其为(c,r)的行程t,Ttime,t即为目标函数值。
点 集V′={(0,2m+n+1),P,D|V′⊂V},其 中,(0,2m+n+1)为车辆c的当前位置和虚拟终点,任一点到虚拟终点的距离均为0。共计m名车外乘客,即未上车乘客,包括已被安排车辆服务但当前时刻还未上车的乘客Q*c和新乘客r,对应上车点P={1,…,m} 和下车点D1={m+1,…,2m} ,各点上车人数qi >0,对应下车人数-qm+i <0;n名车内乘客对应下车点D2={2m+1,…,2m+n} ,下车人数-q2m+i <0 ,其中,q0=q2m+n+1=0 ,下车点集合D=D1⋃D2。此外,记上(下)车点为i或j点所对应乘客r的绕行时间Ri,等待时间Wj(或Wi),车内乘客已在车时间t*c,i,到达目的地最短时间d*i,车辆到达点i的时刻和已载人数Lc,i,惩罚值M。
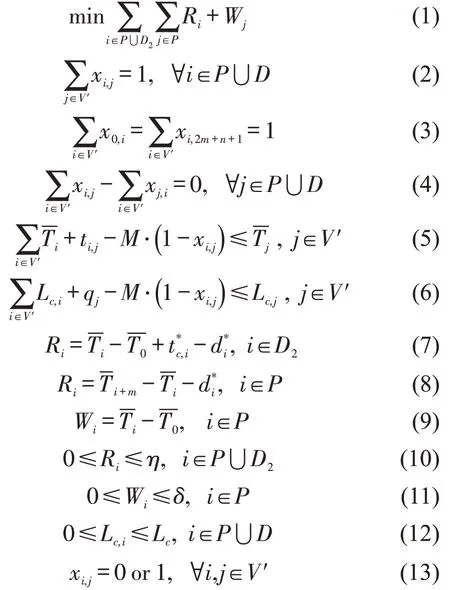
目标函数式(1)保证乘客总等待和绕行时间最少。约束条件:式(2)~式(4)保证流量平衡,式(5)和式(6)保证车辆到达各点的时间和车载能力约束,式(7)和式(8)分别表示车内、车外乘客的绕行时间,式(9)表示车外乘客上车时的等待时间,式(10)~式(12)是对等待、绕行时间,承载能力的约束,式(13)定义决策变量xi,j,当车辆c从点i到点j时取1,反之取0。
不同于文献[3]提出的启发示插入法求解出行路线,本节构建模型并用商业软件GUROBI 计算,不仅能保证找出车辆c的最优路线,还可解决文献[2]和文献[3]中是否考虑排队的两种不同策略,更具普适性。当集合Q*c={}时,即为不排队策略,已安排服务但当前还没上车的乘客将进入下一周期重新优化;排队策略表示上述乘客将按照当前出行方案排队等待服务。
2.3 感知体系
在2.2 节确定(c,r)具体路线方案f*(c,r)(即行程t)后,分别求解行程t中车内乘客感知价值pin,t和车外乘客感知价值pout,t,以及该趟行程中总感知价值Pvalue,t=∑pin,t+∑pout,t。
(1)乘客心理特征
已有研究表明,感知价值与乘客满意度呈显著正相关,感知风险与乘客满意度呈负相关。时间和费用对应感知价值中的功利价值成分,而乘客由于性别及出行目的等不同,对共乘人数常持有积极或消极态度。积极态度包括感知价值中的享乐主义和社会价值,如结交朋友扩大交际圈,减少私家车使用获得社会认同感[4-5];消极态度如侵犯隐私等感知风险[4]。此外,文献[6]考虑时间、费用、共乘人数3 项指标作为乘客合乘决策主要因素。因此,本文选取这3项内容作为量化指标感知乘客心理,并以感知价值(%)表示乘客满意度。
(2)价值函数
在动态合乘问题中,出租车和乘客的出行方案是时刻变化的,具有不确定性。为捕捉不确定下的主观价值,选取前景理论中的价值函数感知量化上述3项指标。具体价值函数为
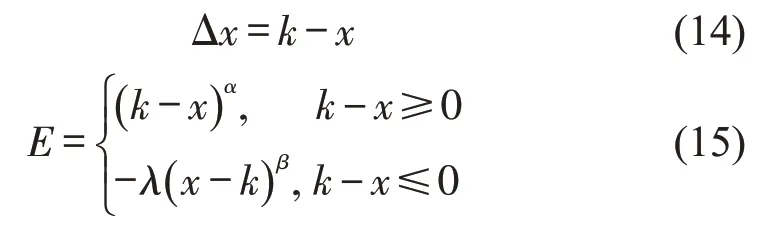
式中:x为某情境下的具体取值;Δx为相对于参照点k的某种收益;α和β为风险态度系数;λ为损失规避系数。根据文献[8],α=0.89,β=0.92,λ=2.25最符合决策者心理特征。
具体对应三要素包括:
① 感知时间价值函数Etime,参照点,ktime为乘客r在当前出行方案中的总时间成本,Δt=k*time-ktime为时间收益。
②感知费用价值函数Ecost,参照点k*cost为原价,kcost为乘客r根据当前出行方案所需支付的费用,Δc=k*cost-kcost为支付优惠,与一人共乘8 折,两人共乘7折,以此类推,最低5折。
③感知共乘人数价值函数Enump,对共乘人数持有积极态度时,参照点为乘客r已与nˉ人共乘;持有消极态度时,乘客最满意的情况是无人合乘,因此乘客在共乘人数一项中只存在最满意和损失心理两种状态。考虑与积极态度保持大小一致以及权重中正负数值关系,令,当无人共乘时Enump=-λ;有人共乘时,
消减不同量纲的计算影响,将各感知价值做规范化处理,构建各因素权重w1,w2,w3(w1+w2+w3=1)的多元线性函数,最终乘客r感知价值pr(区间在(-w3,1])的函数形式为
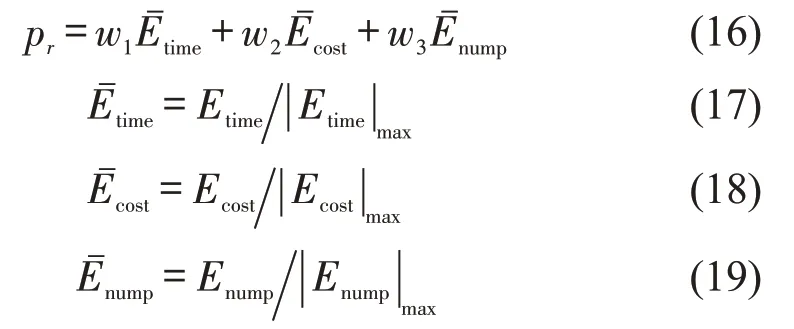
2.4 匹配优化
最终构成Ttrip={(c,r)={t,Ttime,t,Pvalue,t}|c∈C,r∈R} 。由于一个(c,r)对应一个行程t,因此,车辆c完成行程t,即表示车辆c服务乘客r。同时在Ttrip中设立车辆c、乘客r分别与行程t的对应关系:车辆c服务的行程集合Ttrip,c,乘客r所在行程集合Ttrip,r,总行程集合T*trip,服务行程t的车辆c集合Tcar,t。
决策变量εt,c=1 表示行程t由车辆c完成,否则为0;yr=1 表示乘客r未被安排车辆服务,否则为0。


目标函数:式(20)保证总出行时间成本最小化,以避免部分乘客因折扣等原因逗留在车内从而占用道路资源,未被服务的乘客施以惩罚成本M;式(21)保证乘客满意度最大化。约束条件:式(22)保证车辆在一次匹配中最多被分配一位乘客,式(23)保证乘客在一次匹配中最多被一辆车服务。
2.5 求解多目标规划问题
为快速获得2.4 节多目标规划问题的优质解,选择文献[9]提出的EMOABC 算法,其与同类型先进算法相比,具有可实现程度高、控制参数少,快速返回优质解等特点。
EMOABC 采用Pareto 概念,创建外部档案库(External Archive)。每次搜索过程中,为保持种群多样性,避免算法过早收敛。选择档案库中拥挤度最大的精英样本对雇佣蜂、侦查蜂与跟踪蜂改进以产生新食物源,同时档案库根据拥挤度大小存储更新搜索时发现的非支配解。具体可参考文献[9]。
3 实验分析
3.1 实验设置
实验获取海口市经度110.27°E~110.39°E,纬度19.98°N~20.09°N 内的道路网空间数据,并筛除车辆无法通行的道路。以道路网交叉口为节点,交叉口间路段为弧制成路网,共生成1043 处节点和1974条有向路段。
实验采集海口市部分地区出租车订单数据中某日0:00-1:00 这1 h 内的100%和2 倍100%的乘客订单数据,并采用Floyd 法提前求解各点间的最短距离。车辆初始位置随机设置在各节点,并以10 m·s-1匀速行驶,δ=300 s,η=300 s,Lc=4,M=1000,周期t0=30 s。表1~表4均为1 h后的最终优化结果。
重要度权重设为[0.45, 0.35, 0.2],理论上随机排布共有12 种重要度顺序(包含6 种w3为负的消极态度),但考虑到持消极态度的乘客,其不能过于在乎价格等情况,最终w1,w2,w3排序为:[0.45,0.35,0.2],[0.45, 0.2, 0.35],[0.35, 0.45, 0.2],[0.2, 0.45,0.35],[0.45, 0.35,-0.2],[0.45, 0.2,-0.35]。实验中乘客随机获得其中一种重要度偏好。
3.2 不同策略机制分析
设置2组不同乘客和车辆数的实验案例,交叉组合两类策略,共计4 种,计算各自在动态合乘下服务率、平均满意度等方面数值,如表1所示。

表1 4 种策略优化结果对比Table 1 Comparison of results of four strategy models
表1中,Re 为不排队策略,Qu 为排队策略;Pt表示考虑出行效率的同时,感知乘客出行心理,Tn表示仅考虑出行效率而不感知乘客心理。其中,Re+Tn、Qu+Tn分别代表文献[2]和文献[3]中的方法策略。同时对表中服务率等定义为
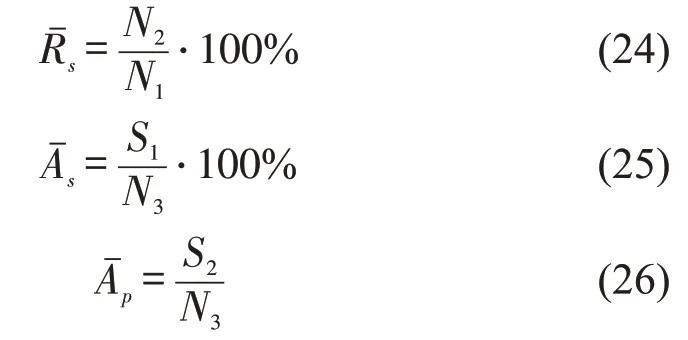
式中:、和分别为服务率、平均满意度和人均耗时;N1为截止到1:00收到的乘客总订单请求;N2为截止到1:00 已服务乘客总数量;N3为截止到1:00服务完成且下车的乘客总人数;S1为截止到1:00服务完成且下车的乘客满意度之和;S2为截止到1:00服务完成且下车的乘客所耗时间成本之和。
同类策略间比较(如表1中实验1 和2 比较Re和Qu、1 和3 比较Pt 和Tn 等)可以发现:相比于Qu策略,Re策略使乘客在上车前,更有可能被分配到更适合的车辆中,因此Re+Tn 比Qu+Tn 人均耗时少,但服务率偏低,而Re+Pt在服务率、满意度等方面均优于Qu+Pt;相比于Tn 策略,加入感知机制的Pt策略通过微观调整匹配方案,可明显提升乘客出行满意度。
因此,综合考虑乘客心理和全局出行效率的Re+Pt策略,能够安排更合理、综合性更强的匹配方案,使其在各组实验中均产生最优乘客满意度,较Tn类策略平均相对提升12%,同时在最终服务率、平均损耗时间方面也保证具有最优或次优表现。而在计算时间上,Pt类策略较Tn类策略,增加了求解感知机制及多目标问题的计算时间;而相较于Qu策略,Re策略使得部分订单不断重新优化,增加了一定计算时间,但均在可接受范围内。
3.3 算法对比分析
为验证EMOABC 求解多目标问题的有效性,与非支配排序遗传算法(Non Dominated Sorting Genetic Algorithm-II,NSGA-II)[10]、Pareto 准则和经典人工蜂群算法[11]结合的多目标人工蜂群算法(Multi-Objective Artificial Bee Colony,MOABC)进行比较。设置2组实验,分别采用3种算法求解,各测算5次,数据取5次最终服务结果的平均值,结果如表2所示。设置控制参数,种群数60,最大迭代数200,外部档案库规模为5。
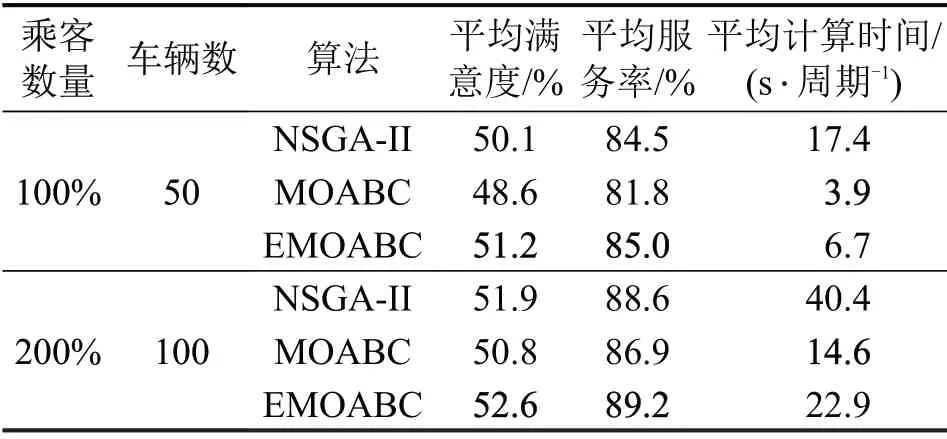
表2 算法性能比较Table 2 Algorithm performance comparison
由表2可知,NSGA-II算法求解时间过长,且平均满意度均劣于EMOABC;MOABC 算法求解时间最短,但其过早收敛,获得较差解;EMOABC在2组实验的求解质量上均达到最优,平均满意度较MOABC 相对优化4.4%,较NSGA-II 优化1.7%,计算时间为次优,综合表现更佳。
3.4 车辆数灵敏度分析
为分析车队数量对优化结果的影响,在其他条件不变的情况下,改变车辆数进行求解,结果如表3所示。
由表3可知:对于Pt 类策略,车辆数增加为匹配机制提供更多兼顾满意度和出行效率的可行方案,故企业在实际应用中可通过适当增加车辆数的方式,有效提升满意度、服务率,降低人均耗时;对于Tn 类策略,以出行效率为导向的匹配机制优先实现出行效率最高(出行成本最小)的匹配方案,故服务率得到提升,人均耗时下降,但满意度降低。
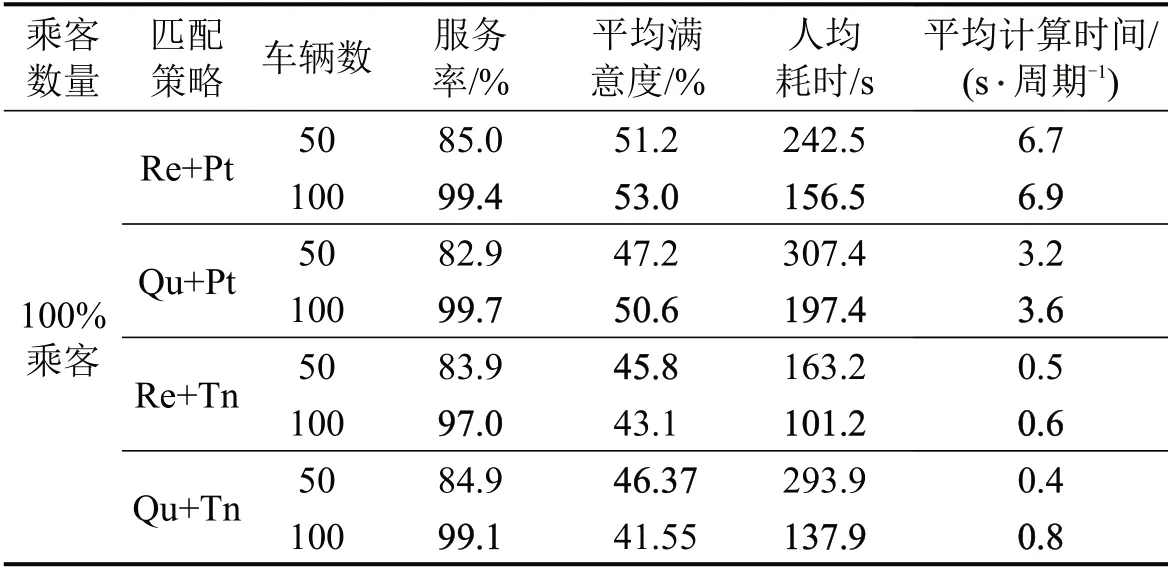
表3 不同车辆数优化结果Table 3 Optimization results under different number of taxis
3.5 周期灵敏度分析
其他条件不变的情况下,改变周期时长t0,以分析其对优化结果的影响,结果如表4所示。
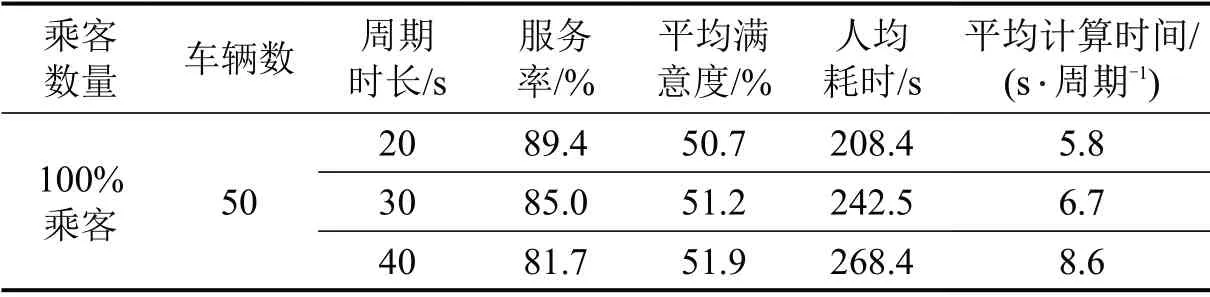
表4 不同周期优化结果Table 4 Optimization results under different period
由表4可知,周期越短,服务率越高,满意度越低。这主要是因为同样时间内,周期越短,1名乘客可被重新优化的次数就越多,即增加了其与车辆匹配的可能性,故服务率提升;因式(20)中M对可被服务的乘客具有一定强制性,故部分乘客以较低的满意度完成出行服务,从而造成满意度降低。
4 结论
乘客出于个人原因对合乘决策中价格、时间,共乘人数有不同喜好,本文通过感知模块捕捉乘客心理,并运用到合乘问题中的匹配规划模块。所提出的算法框架,能够巧妙处理动态合乘问题所涉及的匹配、调度和感知间的复杂关系,并保证在有限时间内得到优质解,这是单个算法或模型难以解决的。多次实验表明,本文提出的Re+Pt优化策略综合表现最优,不仅能够较大改善乘客合乘中的出行体验,同时服务率也能保持次优及以上水平,尽管人均耗时较最优解有所差距,但对乘客来说,这也是其更愿意接受的情形。本文研究内容为应用于实际场景,改善企业服务水平,提供基本策略和理论方法指导。
