考虑空车调配协调的货物列车开行方案优化研究

刘晓伟，晏启鹏，倪少权*，吕苗苗，吕红霞

(1.西南交通大学，a.交通运输与物流学院，b.综合交通运输智能化国家地方联合工程实验室，c.综合交通大数据应用技术国家工程实验室，成都610031；2.四川旅游学院，成都610100)

0 引言

目前，国内铁路货运组织方法，存在一定的局限性，即列车编组计划与运行图等基本计划编制是以计划车流为基础，而计划车流无法反映基于货运营销与动态需求确定的日常动态车流，使得在日常调度中按基本计划要求为日常车流分段规划的运送方案尚需优化，加之运送方案规划未考虑运到期限要求，受动态车流及列车满轴开行要求影响兑现困难，导致车流挂线不确定，规划方案难以适应货主动态需求和运到期限要求。因此，文献[1]借鉴客运组织理念提出动态规划型运输组织思想，即依据基本计划与货运营销，基于近期(周、日)动态车流与运到期限要求，调整编组方案与安排运行线等资源，制定车流全程运送方案，滚动编制货物列车开行方案、列车运行计划、机车车辆运用计划等动态运输计划，作为日常调度依据，实现按图行车。加拿大等国外铁路以分组列车形式为主的规划型运输组织方法[2]，不完全适应国内以单组列车形式为主的运营特点。

货物列车开行方案是基于动态车流进行编组计划调整与列车运行方案综合优化，确定列车径路与编组内容、开行频率及时段，为后续安排运行线确定列车运行计划提供依据，属于动态服务网络设计问题[3]；列车运行方案是在基本运行图架构[4]中为列车挑选合适区段线。实际中，空车调配及时与否直接影响货物装卸取送作业、车流开始集结时段及列车集结过程，其合理性也将影响货物列车开行方案优劣，要求两者协调优化。

既有研究主要集中于空车调配、列车开行方案优化问题，较少涉及两者综合优化研究。国内学者基于多阶段[5]、多时点[6]优化策略，国外学者考虑市场动态需求[7-8]、基于列车时刻表[9-10]研究空车调配问题。关于列车开行方案的研究成果，可参考文献[4]分析，其考虑车流改编方案唯一性与树形改编要求、运到期限等约束，优化列车开行方案，但未考虑空车调配协调问题。两者综合优化研究较少，HAGHANI[11]以美国铁路为例，研究列车径路、编组计划与空车分布的综合优化；ANDERSEN 等[12]以欧盟铁路为例，考虑多类型车辆周转的货运服务网络设计问题，但国外铁路较少考虑车流不可拆分与树形改编要求。文献[13]针对国内铁路，考虑车辆周转设计铁路动态服务网络，未考虑车流树形改编要求、车站能力限制以及节点与区段不对流空车约束。本文以单组列车形式为主，考虑空车调配协调研究货物列车开行方案优化问题；以文献[4]为基础，在目标中考虑空车配送费用，结合配空与装卸取送、集编发的时间接续要求、节点与区段不对流空车要求，进行重空车流组织优化。

为避免引入空车调配因素导致车流组织方案数量激增和求解复杂度增加的问题，基于车流时空服务径路构建弧路模型；借鉴文献[14]中k短路算法快速搜索重车、空车流时空服务径路可行集，减小问题规模。结合重车或空车配空的时间接续要求，将不同的k短路重车流方案与空车配空方案相关联，改进文献[4]的可行解构造方法，设计混合差分进化求解算法。

1 基于时空网络的重车、空车流动态组织过程分析

为分析空车调配对动态车流组织过程的影响，根据文献[6]配空与装运关系描述，拓展文献[4]中基于离散时空网络方法构建的货运时空服务网络，结合基本运行图架构与车流径路，确定网络结构，引入货场时空节点，重车装取与送卸弧及空车取送弧，刻画配空与装卸取送、集编发的时间接续关系，分析各重车、空车流在网络中寻路过程，将车流按一定规则分配到合理时空服务弧上，确定重车流时空服务径路与空车配送方案，新增集合和参数如表1所示，重车、空车动态组织过程如图1所示。

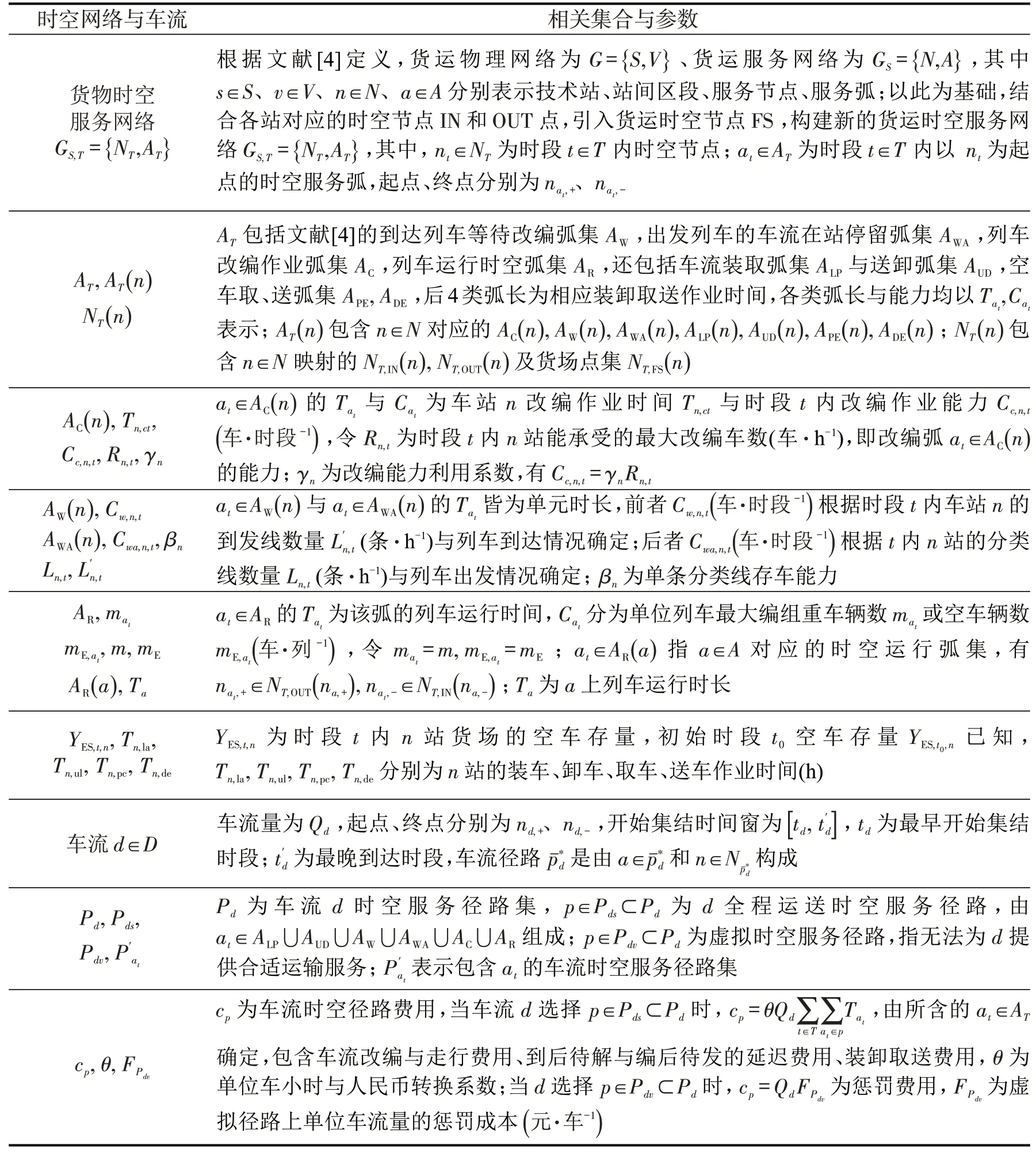
表1 时空网络与车流的集合与参数Table 1 Sets and parameters of space-time service network and wagon-flow

图1中，i1,i2,…,i8,i9为不同时空节点，假定装卸车、取送车等四项作业时长均为1 个时段，可依据实际情况调整；假设长途车流在S3站改编，当空车充足，其与短途车流分别选择第2,2,6 时段开始集结，车流时空运送方案为；当S3站空车不足，装车将受影响，一方面，选择开行空车直达列车为S3站提供空车，则各车流方案不变，空车调配费用随之增加；另一方面，利用到站车流完成卸车，进行重车配空，将在第9时段开始集结，方案变为，车流集结等待费用随之增加。显然，考虑空车调配协调，决策配空方案，对作业车流配合中转车流集结编组及时挂线产生重要影响。

图1 货运时空服务网络与车流时空服务径路Fig.1 Car space-time path in freight transportation space-time service network

2 模型构建

2.1 模型假设

(1)快运、装车地直达列车编组方案和运行线安排已确定，空车直达列车方案未知，主要研究空车直达列车、技术直达列车和相邻编组站间的列车编组方案与运行线安排综合优化。

(2)车流OD量、运到期限要求、车流径路已知；车流起运时段未知，即开始集结时段未知，需根据重车、空车流组织和时间窗要求进行决策。

(3)基本运行图架构已确定，按时段描述区段通过能力；根据实际数据，采用单元时段换算，近似描述各弧时长。

(4)实际中车流不允许拆分且需满足改编方案唯一性，可以假定车流需要满足时空服务径路唯一性要求。另外，不考虑空车车种和重空混编方式，假定车站装卸取送作业能力充足。

2.2 决策变量与中间变量

xp∈{0,1} 为重车流d∈D是否选择时空服务径路p∈Pd运送；xd,a∈{0,1} 为车流d是否选择列车运行弧a；xE,i,j∈{0,1} 为节点i,j∈N之间是否开行空车直达列车；yE,at为选择时段t内时空弧at的空车流量；fat∈Z0+,fE,at∈Z0+为时段t∈T内运行时空弧at∈AR上开行重车流、空车流列车的频率，Z0+为正整数集；∈{0,1} 为相同到站车流的树形运输决策变量[4]，若终点为n站的车流d，在同一技术站n′∈改编后，选择列车运行弧，即n′站(na,+站)的后续改变站为na,-站时，1；否则，0。其中，为终点为n站的车流d的车流径路，显然为所含车站集。

2.3 模型建立

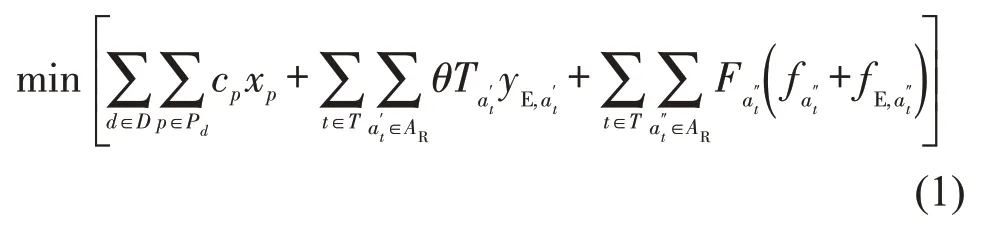
式(1)为动态车流组织优化模型目标，使规划期内重车流径路费用、空车走行费用、列车开行费用的广义总费用最小；a′t∈AR、a″t∈AR均为运行时空弧，Ta″t为a″t∈AR上列车运行时长，单位列车开行费用α为单位列车固定开行费用(元·车-1)；指运行时空弧a″t∈AR上单位列车每运行1 时段的燃油费用(元·时段-1)。式(2)为重车流时空服务径路唯一性约束。式(3)、式(4)为车流改编径路唯一性约束与树形改编约束。式(5)为重车流选择列车运行弧与时空服务径路的关联约束，当车流d选择运行弧a时，才能选择包含a对应的运行时空弧at∈AR(a)的时空服务径路式(6)、式(7)为节点与区段不对流空车约束，节点h∈N不允许同时存在到达、出发空车流，且区段v∈V不允许同时存在正向、反向空车流。式(8)为空车流选择列车运行弧与运行时空弧的关联约束，当节点i,j∈N允许开行空车直达列车，空车流才可选择nat,+∈NT,OUT(i),nat,-∈NT,IN(j)的运行时空弧at∈AR。式(9)为重车、空车流转换关联约束[11]，是时段t内n站的空车分配决策，左侧为空车供应，即时段t内n站空车存量、到达空车量与完成卸车的到站重车流量三者之和；右侧为空车需求，即时段t+1 内n站空车存量、时段t内n站为其他站配送的空车量与开始装车的重车流量三者之和。式(10)、式(11)为列车运行时空弧的运输能力约束，ηmat,ηmE,at分别为at∈AR上单位列车最小重车或空车编组辆数；d:p∈Pd为车流d通过时空服务径路p,即两者相关联。式(12)、式(13)为区段通过能力约束，指列车运行弧a若需正向或反向途经区段v，其通过v的后方全部区段所需时长；Cv,t,Cvˉ,t指时段t内区段v的正向、反向通过能力(列)。式(14)～式(16)为技术站能力约束，依次指改编作业能力、到发线与分类线数约束。

3 算法设计

通过表2建模特点分析可知，本文模型引入的空车调配约束较复杂，既有算法[4,13]均难以快速有效处理，故本文结合重车或空车配空的时间接续要求，通过k短路搜索与可行解构造，将退火机制引入差分进化算法(DE)进行求解。

表2 本文建模特点分析Table 2 Model characteristic of this paper

(1)k短路搜索与可行解构造

借鉴文献[14]中k短路算法搜索重车、空车流时空服务径路可行集，以减小问题规模。并结合重车或空车配空的时间接续要求，将不同的k短路重车流方案与空车配空方案相关联，引入贪婪策略、退火策略，改进文献[4]的可行解构造方法，可行解构造流程如图2所示。

图2 可行解构造流程Fig.2 Flow diagram of constructing feasible solution

①基于贪婪策略的关联与配空方案初选

当k值确定，若基点或关联车流dl起点站空车充足，则根据不同时空径路序号q值，分别以φk,q,dl为起点，按重车流约束与合并开行要求，以关联方案费用增长最小、列车开行费用节省最大为原则，依次筛选关联车流dl,RD，确定关联方案tpk,q,dl；否则，按配空要求，以重车配空优先、空车配空次之的原则和配空方案费用排序，为各配空方案设置配空策略编码k′dl∈Kdl，选择k′dl最小的配空方案ECk,q,dl。

②基于退火策略的关联与配空方案比选

以相同k值，不同q值的车流dl方案φk,q,dl为起点，形成不同关联方案tpk,q,dl与配空方案ECk,q,dl，即方案ICk,q,dl，以概率选择较优方案ICk,q,dl，其中，ζk,q,dl,ζmin为各方案ICk,q,dl权值与最小权值，δ为当前温度。

(2)编码与初始种群

根据可行解构造中车流di运送方案φk,q,dl,(k=0,1,2,…,K;q=1,2,3,…,I)的时空径路序号q以及配空策略编码k′dl∈Kdl，设计个体实数编码方案：，其中，I+1 为虚拟径路方案，Kdl+1 表示不需要配空，并以概率ψk,q,dl随机选择方案ICk,q,dl，获得规模为Nps的初始种群。

(3)算子设计与算法流程

算法流程如图3所示。

图3 混合差分进化算法(HYDE)的算子设计与流程Fig.3 Operator design and framework of hybrid differential evolution algorithm

采用常用的DE/best/1 变异策略及交叉、选择策略，GM为最大迭代次数，计算式为

式中：χr1,G,χr2,G为规模为Nps的种群中两个不同个体；变异率F=0.7；rand 表示随机数；D表示车流集合；交叉率CR=0.1 ；χτ,l,G,γτ,l,G,Uτ,l,G分别为个体χτ,G中对应第l支车流运送方案与配空方案的l列原始、变异、交叉后编码。

当变异交叉新个体χτ,G不满足约束，需先根据χτ,G编码确定车流dl改编调整方案和配空策略k′dl，按可行解构造方法获得新解；当配空策略k′dl无效时，则选k′dl最小的可行配空方案。由于可行解构造引入退火策略，故该策略将影响DE算法。

4 案例分析

以我国东北地区某局部铁路网为例[4]，对本文模型及算法进行验证。路网中有19 个站，主要参数详见文献[4]与图4，车流径路与区段通过能力、车流OD 量与车站初始空车存量，限于篇幅不予罗列。 规划期设为T=72 h ；θ=50元·车·h-1；α=3000元·列-1；m=50车 ；mE=60车；500元·h-1；FPdv=1000元·车-1；η=0.9；βn=200车·条-1；γn=0.8。路网结构及相关参数如图4所示。

图4 路网结构及相关参数Fig.4 Structure schematic diagram of railway network and relevant parameters

(1)空车调配影响分析

以线路{1,2,6,10,13,14} 和{7,8,10,11,12} 组成的“十字”子路网为例，根据表3的车流量，假定所有车流的最晚到达时段t′d为16，分别求解空车充足与空车不足情景下的优化方案。若空车充足，优化方案目标值为283500，如图5所示。

表3 子路网的车流OD量Table 3 Wagon-flow volume in sub-network

若空车不足，假定空车存量及装卸取送作业时间如表4所示，则需空车调配和调整图5的方案，引起部分列车开行时段变化及车流集结等待时间增加，优化方案如图6所示，目标值增加18150。

图5 空车充足情形下的优化方案Fig.5 Optimization planning without considering empty car distribution

表4 子路网各站初始空车存量及装卸取送作业时间Table 4 Empty car distribution and relevant parametersin sub-network

图6 空车不足情形下的优化方案Fig.6 Optimization planning when considering empty car distribution

配空方案如下：

②采用重车配空，由于空车直达列车1，占用区段1 →2 在时段1 的能力，列车需时段2 出发，时段5到达车站6；车流占用车站6的40辆空车存量，与中转车流组成列车发出；而到站车流经送卸车作业，为车流提供空车，使得车流在时段11才能完成集结，故中转车流需要多集结等待1个时段，与其组成列车发出。

若未考虑空车调配与列车开行方案协调，比如车站1在时段2发出空车直达列车1，将无法及时满足列车装车需求，导致其中一列延误发车，增加额外等待费用。将两者综合优化，有助于合理安排配空方案，减少空车走行费用，及时满足装车需求，有效保证作业车流配合中转车流集结编组及时挂线，提高方案可实施性。

(2)算法效果分析

HYDE 算法采用C＃编程，其中：K=10,Kdi=20,I=30,Nps=20,CR=0.1,F=0.7，在CPU 为Intel Core E6550,2.33 GHz×2,8 G 内存的PC 机上运行，算法求解性能如表5所示。

表5 算法求解性能分析Table 5 Performance analysis of algorithms

当算例规模较小时，CPLEX、SA及HYDE算法均可获得全局最优解。当算例规模扩大时，CPLEX算法无法在限定时间求得全局最优解；SA 算法收敛速度快，但易于陷入局部最优；HYDE 算法收敛较快，求解质量更优。

基于算例Ⅳ的SA、HYDE算法收敛对比如图7所示。

图7 基于算例Ⅳ的SA、HYDE算法收敛对比Fig.7 Convergence curve of algorithm

不考虑节点与区段不对流空车约束，目标值减小，表明该要求对优化方案造成重要影响；HYDE算法能有效处理该约束，获得更切实际的优化方案。

5 结论

为实现空车调配与列车开行方案协调优化，本文考虑配空与装卸取送、集编发的时间接续要求、节点与区段不对流空车要求，构建切合实际的整数规划弧路模型，同时决策列车径路与编组内容、开行时段与频率及空车调配方案等。依据重车、空车流方案的关联性与编码设计，设计混合差分进化求解算法，有效平衡种群多样性与收敛速度。算例结果表明，模型和算法有效，有助于减少空车走行费用，及时满足装车需求，协调车流组织各环节，提高方案可实施性，保证流线结合与运到期限。