考虑碳排放的港口全要素生产率及影响因素分析

戈艳艳，王姗姗

(浙江工商大学杭州商学院，杭州311500)

0 引言

港口，尤其海港，是国际物流网络中无可替代的重要节点，是实现海上丝绸之路互联互通的重要基础。但港口的建设、运行、发展等一切活动都不可避免地会对港口资源和生态环境产生直接或间接的影响，港口也是能源消耗的重点领域[1]。如何建设绿色生态港口，优化港口资源配置是港口未来发展关注的重要领域。基于此，在保持港口可持续发展的前提下寻求港口效率提升，有利于兼顾港口发展和节能减排双重目标，也是现阶段经济环境和生态环境大趋势下港口摆脱发展困境，在世界经济大潮中实现可持续发展的重要途径。因此，本文在考虑碳排放量的基础上测算港口全要素生产率并厘清其影响因素，提出改善港口效率的可行路径，为港口制定可持续发展战略提供有效的理论依据。关于全要素生产率的核算，主要有代数指数法(AIN)、索洛余值法、随机前沿分析法(SFA)和数据包络分析(DEA)这4种。采用较多的是DEA法，为考察全要素生产率的变化，学术界构建了一系列基于DEA 的生产率指数[2]，普遍采用Malmquist 指数分解分析生产率。Nwanosike F.等[3]采用Malmquist指数研究了尼日利亚6 个主要港口改革前后的对比情况。Antonio Estache 等[4]用Malmquist 指数计算和分解墨西哥11个主要港口在基础设施方面的生产率变化。李电生等[5]用DEA 二次相对评价模型分析港口物流效率，提出测算港口物流效率的公式。宋京妮等[6]采用SBM-undesirable 模型分析了中国综合运输效率。曹玮等[7]采用DEA 和Malmquist指数考查了福建沿海港口全要素生产率的变化。艾亚钊等[8]采用SFA模型分析了集装箱港口效率。

诸多学者基于DEA或者SFA模型研究了港口效率，但还存在一些问题：首先，大多数研究采用传统的DEA 方法，部分结合了基础的Malmquist 指数，将生产率指数分解为技术进步率和技术效率变化率，但Malmquist 指数使用的距离函数无法考虑减少污染的情形[9]。近年来，绿色环保重视程度高，可持续发展的新型绿色港口是未来港口经济发展的主流趋势，缺少非期望产出的港口效率测度不再适应市场需求，故本文采用全局Malmquist-Luenberger 指数模型(GML 指数法)，在效率测算时同时考虑非期望产出。目前，将GML 指数法应用在港口效率测度的研究比较少，主要应用在环境效率研究。郭莉[10]等采用SBM-GML指数模型分析了电力行业环境效率区域差异。吕晓剑[11]等基于SBM-GML指数模型分析了山东省大气环境效率时空分异与影响因素。其次，从已有文献来看，多数文献没有厘清内外部因素对港口效率的影响，故本文在GML 指数模型的基础上，运用面板数据引力模型厘清内外部因素对港口全要素生产率的影响。

1 指标体系和模型方法

1.1 指标体系的建立

采用面板数据，时间跨度为2009-2018年，决策单元为中国沿海19个港口，如表1所示。在测量港口生产率时考虑非期望产出，港口全要素生产率评价采用的投入指标主要有港口泊位数、泊位长度、港口机械设备、堆场面积、员工数量等，产出指标主要有货物吞吐量、集装箱吞吐量、港口利润等。鉴于统计数据的可得性，港口机械设备、员工数量、堆场面积和港口利润等数据收集困难，故本文在不考虑这些因素对港口生产率的影响下，选取港口生产泊位数，泊位长度和万吨级以上泊位数作为投入指标，港口货物吞吐量和集装箱吞吐量作为期望产出指标，港口碳排放量作为非期望产出进行研究。港口数据来自历年《中国港口年鉴》和各地方统计年鉴。

表1 决策单元Table 1 Decision unit

我国港口碳排放计算主要依据国际公认的相关准则(温室气体协议、空气质量和温室气体工具、碳足迹指导文件等)、港口碳排放核算对象范围(根据港口货物吞吐量折算成标准煤，2011年后交通运输部开始对交通运输能源消耗进行监测，形成国家统一的能源消耗数据表，年均下降约3%)和我国港口碳排放计算基础数据(港口货物吞吐量)。其中，港口碳排放系数采用国家发改委能源研究所的推荐值0.67，即1 t碳燃烧后产生大约3.67 t的CO2，利用碳排放系数0.67计算，1 t标准煤在大气中燃烧可产生2.4589 t的CO2[12]。港口碳排放计算公式为

式中：C为港口碳排放量；SC为当年标准煤消耗量；HC为当年货物吞吐量；β为碳排放系数，取2.4589。

1.2 模型

Malmquist 指数法由StenMalmquist 于1953年提出，用于分析不同时期的消费变化。Chung 等[13]对距离函数进行了有效拓展，形成方向距离函数，并提出Malmquist-Luenberger(ML)指数。ML 指数采用两个时期指数的几何平均形式，存在潜在的不可行解且不具备循环和可加性，Oh[14]提出一种新的方法——全局Malmquist-Luenberger(GML)指数，可以处理多产出和多投入以及环境恶劣产出，同时避免ML 指数的缺点。因此，本文通过对GML 指数模型拓展，研究港口全要素生产率。

决策单元有X个投入，Y个期望产出，B个非期望产出，第i个决策单元t时期的投入向量xit=(ait,bit,cit)，其中，ait,bit,cit分别为在t时期第i个港口的泊位长度、泊位个数、万吨级以上泊位个数；期望产出向量yit=(dit,eit)，其中，dit,eit分别为在t时期第i个港口的货物吞吐量、集装箱吞吐量；非期望产出向量bit=(fit)，其中，fit为在t时期第i个港口的碳排放量。则

式中：MLt,t+1为ML 指数变化；MLECt,t+1为技术效率变化；MLTCt,t+1为技术进步变化；xt为投入；yt为期望产出；bt为非期望产出；()xt,yt,bt;yt,bt为基于同期生产可能集的方向距离函数；(xt,yt,bt;yt,bt)为基于全局生产可能集的方向距离函数，GMLt,t+1为GML 指数变化；TEt为技术效率；BPGG,t为技术进步；GMLECt,t+1为技术效率变化；GMLTCt,t+1为技术进步变化。 如果GMLECt,t+1＞1，那么t+1 时期较t时期更接近当前生产前沿面，即效率更高；如果GMLECt,t+1＜1，那么t+1 时期较t时期更远离当前生产前沿面，即效率更低；如果GMLTCt,t+1＞(＜)1，那么t+1 时期较t时期更接近(远离)全局生产前沿面，因此，GMLTCt,t+1＞1，即技术进步，GMLTCt,t+1＜1，即技术退步。如果两个时期的输入和输出没有变化，GMLt,t+1=1；如果生产率有所提高，GMLt,t+1＞1；降低，则GMLt,t+1＜1。与传统的ML 指数的几何平均形式不同，GML指数是循环的。

2 实证分析

分析中国沿海19个港口，数据统计特征如表2所示。

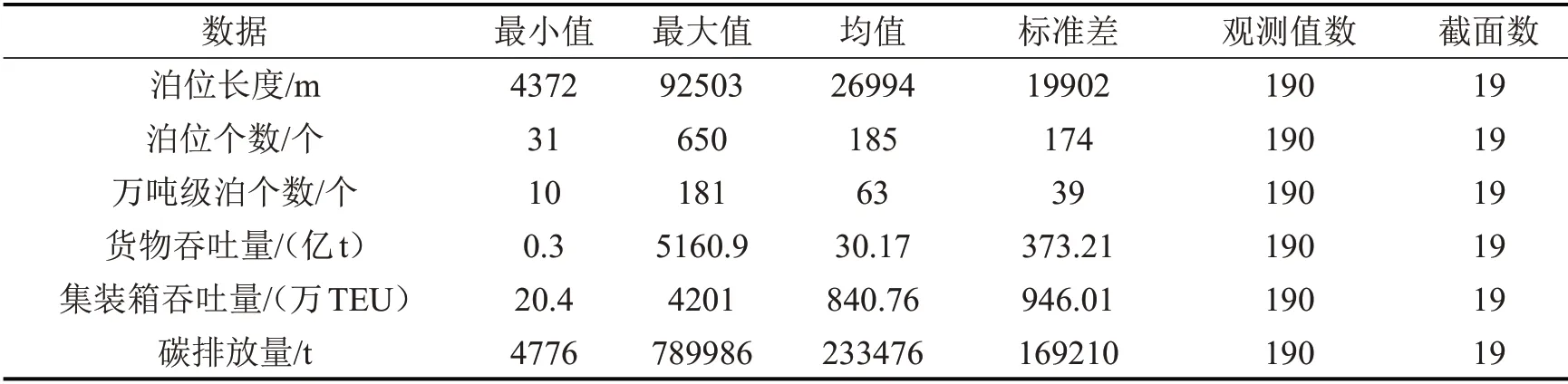
表2 数据描述性统计特征Table 2 Descriptive statistical characteristics of data

2.1 港口全要素生产率相关指数分析

根据式(1)和式(3)，采用Matlab2016求解，结果如表3所示。

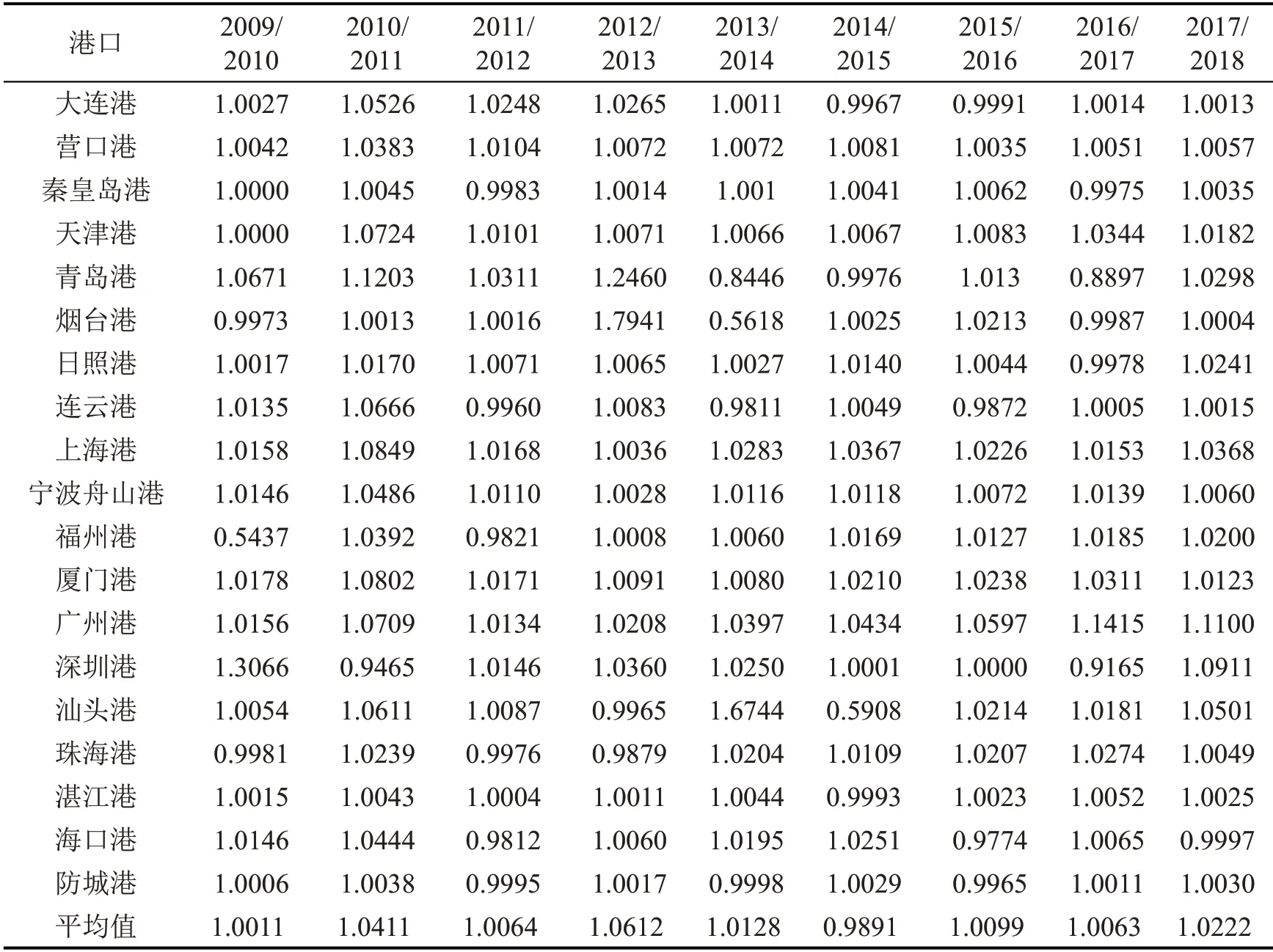
表3 主要沿海港口的GML指数(2009-2018年)Table 3 GML index of major coastal ports from 2009 to 2018

我国主要沿海港口的GML 指数表明：2009-2018年，各港口的全要素生产率都有不同程度的提高，部分港口持续增长，如营口港、天津港、上海港、宁波舟山港等；部分港口增长、降低交替出现，如青岛港、福州港、珠海港等。由此可见，持续增长的港口主要是近几年发展较快的港口，且货物吞吐量大的港口生产率指数不一定高，如上海港生产率指数经常低于深圳港。

从各个年份具体来看，2017/2018年，除海口港生产率水平为0.9997，其他均大于1.0000，说明2017/2018年中国大部分沿海港口生产率有所提高。广州港2014-2018年，生产率指数均高于其他港口，可见广州港近几年发展较快，值得其他港口学习。从各个年份的平均值来看，只有2014/2015年平均值小于1，此期间汕头港的全局生产率指数只有0.5908，处于一种严重恶化状态。

表4为主要沿海港口技术效率变化。可知，2009-2018年，各港口的技术效率都有所降低。具体从各个年份来看：2009-2013年，各港口技术效率变化不大，大部分港口技术效率变化值降低，但降低率较小；2013-2014年，港口技术效率值均降低，且降低速度较大；2014-2015年，大部分港口技术效率值大幅上升；2015-2017年，技术效率变化值基本维持不变。

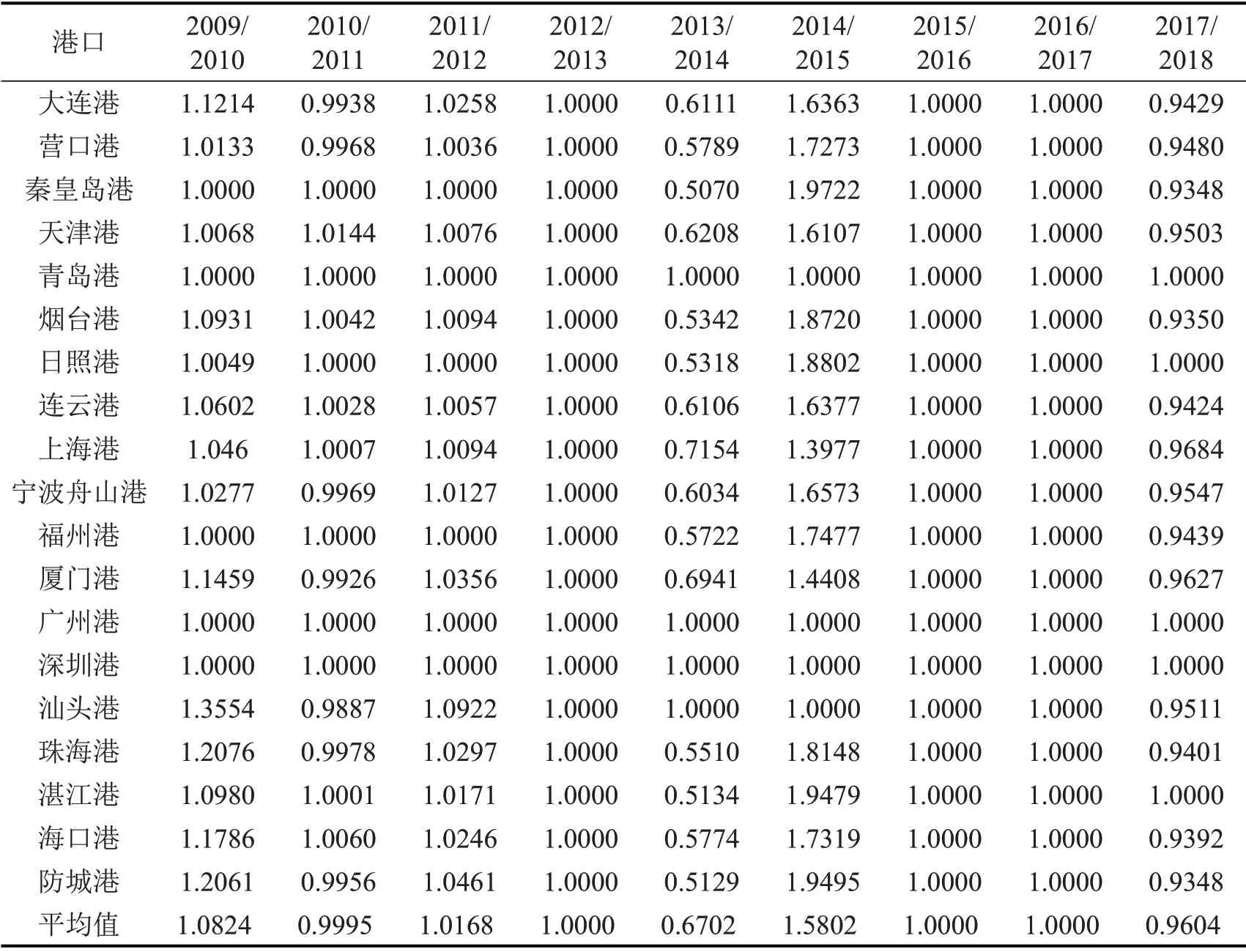
表4 主要沿海港口技术效率变化(2009-2018年)Table 4 EFFCH of major coastal ports from 2009 to 2018

表5为主要沿海港口技术进步变化。可知：2009-2018年，各港口的技术进步有所提高；具体到各个年份来看，2014-2015年大部分港口技术退步，人才流失是其原因之一。

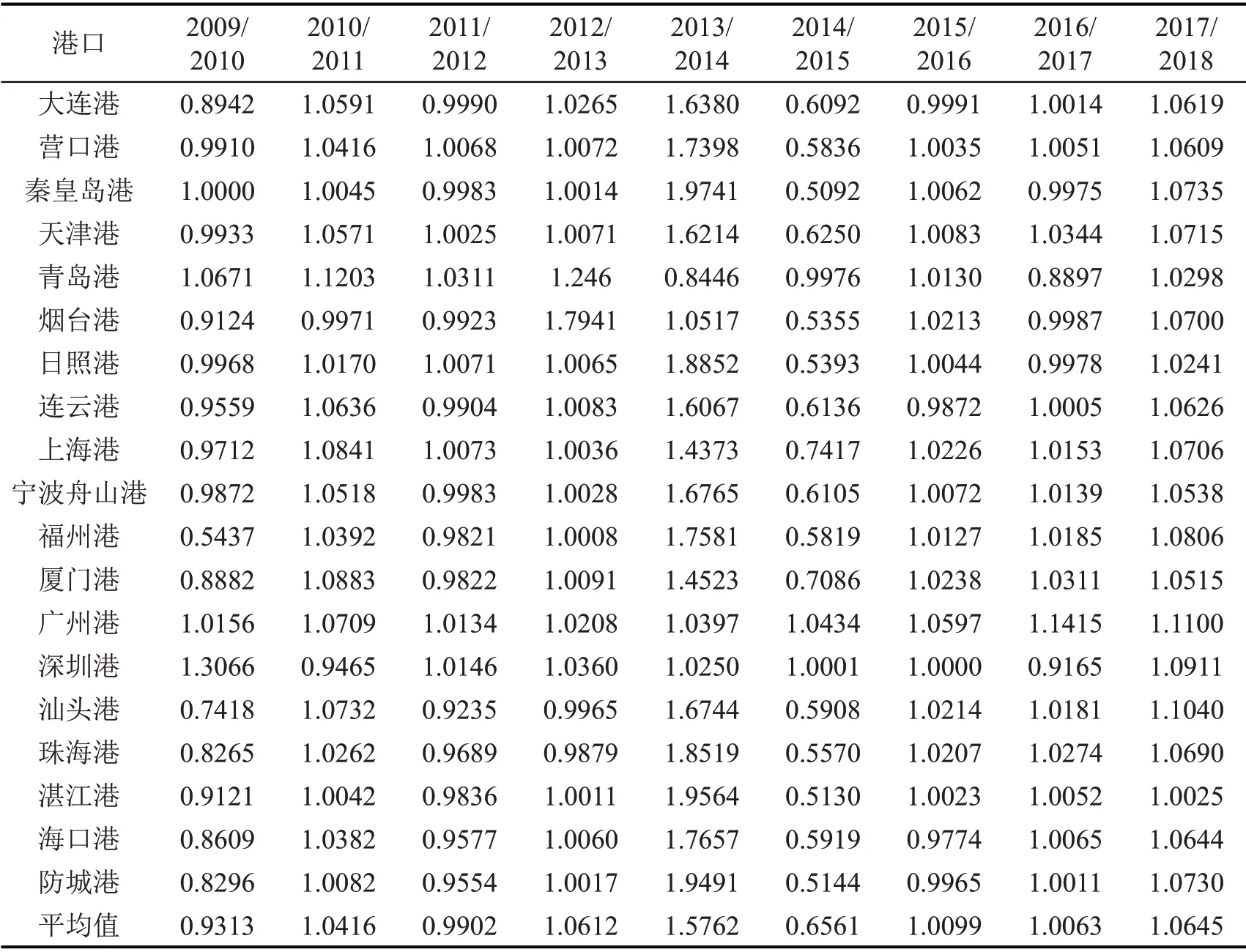
表5 主要沿海港口技术进步变化(2009-2018年)Table 5 TECH of major coastal ports from 2009 to 2018

主要沿海港口GML 平均值、技术效率平均值、技术变化平均值如图1所示。各主要沿海港口：GML 平均值最高的是广州港，为1.0572，最低的是福州港，这主要是因为2009-2010年，福州港GML 值严重降低，2010-2011年又有所降低；技术效率平均值均大于等于1.0000，均值最大的是防城港；技术进步平均值均大于1.0000，均值最大的是秦皇岛港。

图1 GML、GMLEC、GMLTC均值Fig.1 Mean values of GML,GMLEC,GMLTC

五大港口群GML 指数平均值如图2所示。东南沿海地区受福州港影响，2009-2010年GML均值较小，随后比较稳定；长江三角洲地区和西南沿海地区均较稳定；环渤海港口区和珠江三角洲地区较不稳定，时高时低。

图2 五大港口群GML均值Fig.2 Mean values of GML for five port clusters

2.2 港口全要素生产率影响因素分析

为进一步明确各港口GML 指数，技术效率变动，技术进步变化之间的关系，采用面板数据模型对其进行建模分析。港口生产率除了受港口自身发展因素影响，还与城市人均GDP，城市外贸进出口额，交通基础设施等因素相关。将港口效率变动指数GML 作为被解释变量，技术进步变化指数GTECH、技术效率变化指数GEFFCH、城市人均GDP 增长率、社会商品零售总额增长率、货物进出口总额增长率、货物运输总量增长率作为解释变量建立模型。城市人均GDP、社会商品零售总额、货物进出口总额、货物运输总量数据主要来源于国家统计局网站及各城市统计年鉴。

面板回归模型为

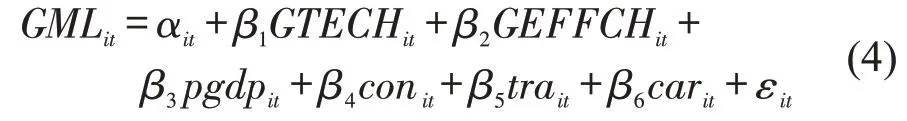
式中：下标i,t代表港口城市和年份；GTECHit为技术进步变化指数；GEFFCHit为技术效率变化指数；pgdpit为人均GDP增长率；conit为社会商品零售总额增长率；trait为货物进出口总额增长率；carit为货物运输总量增长率；αit为常数项；εit为随机扰动项；β1～β6为变量系数。

采用eviews9 建立面板数据模型，经hausman检验的统计量为2.388966，伴随概率为0.8807，不拒绝原假设，建立随机效应模型，结果如表6所示。

表6 模型估计结果Table 6 Result of model

结果表明，港口效率GML 指数除受内部因素影响，还与货物进出口总额有关，这一结论与文献[15]的研究结论基本相符，货物进出口总额增长率每增长1 个百分点，港口效率GML 指数提高0.049242个百分点，其他外部因素影响不显著。

3 结论

本文基于DEA 方法，结合方向距离函数构建含非期望产出的港口生产率模型，运用该模型对中国主要沿海港口2009-2018年间港口生产率GML指数进行测算和分析，并采用面板数据模型分析港口生产率GML指数影响因素。结果表明：

(1)2009-2018年，中国主要沿海港口的全要素生产率都有不同程度的提高，且持续增长的港口主要是近几年发展较快的港口，但货物吞吐量大的港口GML指数不一定高。

(2)2009-2018年，各港口的技术效率有所降低，其原因是近几年随着港口投入的增加，沿海港口泊位数量和泊位长度投入增大，但产出水平没有同步增长，港口碳排放量没有得到有效控制。因此，港口生产率提升既要提升技术水平，又要提升管理水平。

(3)2009-2018年，各港口的技术进步有所提高，但2014-2015年大部分港口技术退步，人才流失是其原因之一。

(4)主要沿海港口的GML平均值广州港最高，福州港最低；技术效率平均值均大于等于1.0000，均值最大的是防城港；技术进步平均值均大于1.0000，均值最大的是秦皇岛港。

(5)东南沿海地区、长江三角洲地区和西南沿海地区GML 均值较稳定，环渤海港口群和珠江三角洲地区较不稳定，时高时低。

(6)港口生产率GML 指数除了受内部因素影响，还与货物进出口总额有关，货物进出口总额增长率每增长1 个百分点，港口生产率GML 指数提高0.049242个百分点。

近年来，打造“绿色港口”成为港口行业的普遍认识，但没有很好地从技术、管理、规模、节能等角度分析港口生产率，使部分港口在制定策略时存在一定问题，如：一味加大港口建设投入，忽视管理及人才培养等。从本文的实证研究来看，积极采取措施提升港口的技术、管理、规模水平，同时加快城市进出口贸易是现阶段提升港口生产率的有效途径。