考虑政府补贴决策的中欧班列竞合关系研究
2021-04-28张蒙蒙许茂增
张蒙蒙,许茂增
(重庆交通大学,经济与管理学院,重庆400074)
0 引言
在一带一路倡议深入实施推动下,中欧班列发展势头迅猛,数量规模呈现井喷式增长[1]。中欧班列已经成为中欧贸易中货物运输的重要依托方式之一。与海运、空运相比,可靠性是中欧班列发展的特色[2]。但中欧班列的发展仍不成熟,面临着诸多问题,如货源地竞争激烈,中欧班列的运营平台公司在地方政府的补贴下竞相低价揽货,竞争失衡,市场失序偏离了市场运行的客观规律,这将影响中欧班列高质量发展[3-5]。
在中欧班列竞争中,地方政府发挥了不可忽视的作用。早期,为培育和促进中欧班列发展,地方政府给予适当补贴是必要的,这也是中欧班列高速发展的重要支撑条件之一。但是近几年,随着各地纷纷开行中欧班列,平台公司的数量不断增多,但班列组织仍是以各个平台公司为核心开行单一形式的直达班列[6]。因此,货源竞争愈演愈烈,在政府补贴的支持下,平台公司忽视运营成本与运作效率低价揽货。这种无序竞争会造成严重的资源闲置浪费,进而影响中欧班列的长期可持续发展。国家财政部要求地方政府降低补贴标准,但部分地方政府并没有严格执行相关规定,而是将补贴转化为其他形式[3]。为缓解恶性竞争,中欧班列平台公司及地方政府可以利用自身优势条件在资源整合、统一调度等方面进行合作。目前,中欧班列之间的合作竞争已初现端倪。重庆、成都开行的中欧班列在政府“共建双城经济圈”政策的推动下,开展口岸互联、通道资源共享、境外节点协同等合作。但仍缺少利用数学模型分析中欧班列竞争与合作关系的研究。
中欧班列政府补贴问题已成为学者们研究与业界关注的热点。孙彩虹等[7]研究了中欧班列政府补贴的退出条件,认为构建跨国双向供应链是政府补贴退出的可能选择。谢雨蓉等[8]发现,中欧班列的发展受政府补贴和政策创新等因素影响,运用数学模型研究了中欧班列与班轮之间的运价竞争,以及在政府不同的补贴决策下,中欧班列企业的发车间隔情况。Kundu等[9]研究了政府补贴决策对中欧班列铁路运输与海运之间竞争的影响,发现政府补贴会影响托运人对货物出口运输方式的选择。Feng等[5]基于地方政府和平台公司构建补贴模型,研究地方政府的最优补贴值。
现有研究大多以平台公司与地方政府的纵向关系探讨政府补贴问题,而本文研究区域内两家平台公司和地方政府两个层面上的合作与竞争问题,以及政府以社会福利为最大化目标的补贴决策问题。
1 基本模型
考虑区域内由两个地方政府和两个平台公司组成一个两层国际铁路运输服务系统,其中两个地方政府分别对本地的平台公司提供补贴政策,图1为系统中的竞争关系。在该系统中,将地方政府看作是博弈的参与者,处于第一层的地方政府通过补贴决策以实现社会福利最大为目标。地方政府在对班列的运营补贴上存在竞争,为的是提高本地中欧班列在货源竞争上的优势。处在第二层的平台公司是协调托运人与铁路承运人的中间商,同时提供国际铁路货运代理业务,平台公司之间进行发送量竞争,目标是实现利润最大化。

图1 基本框架Fig.1 Base framework
假定对于两个平台公司(i∈{ }1,2 ,j=3-i),市场可以划分为M1、M2和N1这3个部分。其中,市场M1和M2的货源分别由平台公司1和平台公司2主要负责,需求量主要受本地平台公司的运价影响;市场N1由两个平台公司相互竞争获得,需求受两个平台公司的价格和交叉价格影响。用上角标M 表示市场M1 和M2 中的参数,上角标N 表示市场N1中的参数,其他参数含义如表1所示。

表1 主要参数Table 1 Main parameters
平台公司i在市场中的价格为和,需求为和,需求总和为根据Jiang等[10]的研究,平台公司的逆需求函数为
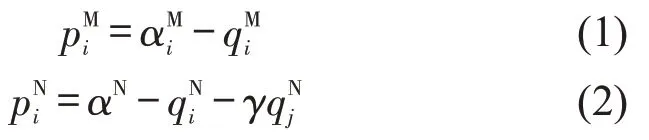
式中:γ∈(0,1)为竞争强度系数,表示平台公司j的发送量对竞争对手价格的交叉影响,同时也表示两个平台公司间的竞争强度;和αN为消费者愿意支付的最大运价。在垄断市场M1和M2中,也可以表示为市场规模;在双寡头市场N1中,市场规模可以表示为。为简便计算,本文假设
平台公司的利润包括3部分:本地市场中由发送量带来的收益,竞争市场中由发送量带来的收益,以及政府根据总发送量给予平台公司的补贴。故平台公司决策发送量qMi,的利润函数为

地方政府在考虑社会福利最大目标下确定补贴值的大小。社会福利W包括平台公司的利润、消费者剩余与社会效益之和减去补贴总额[8]。根据Singh 等[11]和Jiang 等[10]的研究,地方政府考虑的本地消费者福利可以表示为根据谢雨蓉等[8]的研究,地方开行中欧班列带来的社会效益系数为θ,社会效益为可以看出,平台公司的集装箱发送量直接影响平台公司的利润、消费者剩余以及社会效益和补贴总额,从而影响地方政府决策补贴的社会福利函数。因此,地方政府决策补贴si的社会福利函数为

平台公司和地方政府根据自身的目标函数选择最优策略。博弈的决策顺序为:首先,地方政府根据社会福利最大化制定补贴策略;然后,两个平台公司根据政府提供的补贴进行发送量竞争。根据逆向归纳法得出均衡解,本文用上标符号“^”表示均衡解,符号“~”表示最优响应函数。
考虑3 种情形的竞争与合作:情形B 为地方政府与平台公司分别各自决策,不存在合作关系;情形F 为地方政府不合作,平台公司合作;情形G 为两地地方政府牵头合作,平台公司也合作。用上角标B、F、G分别表示3种情形下的参数。
1.1 情形B 完全竞争
情形B描述了当前的市场现状,两家平台公司在各自地方政府的补贴下进行发送量竞争。在给定补贴情况下,平台公司利润函数式(3)关于发送量的一阶导数为0时,求出平台公司在市场中的需求响应函数为

可以直观地看出:在本地市场中平台公司的均衡需求与补贴呈正相关,提高补贴可以增加本地需求;在竞争市场中两个地方政府的补贴策略对需求有交叉影响,本地政府提高补贴,平台公司的需求增加,竞争对手的需求下降。
将需求响应函数代入政府的社会福利函数式(4)中,并根据补贴si的一阶条件求出均衡补贴为

将最优补贴代入响应函数式(5),式(6),可以得到平台公司在两个市场中的发送量分别为
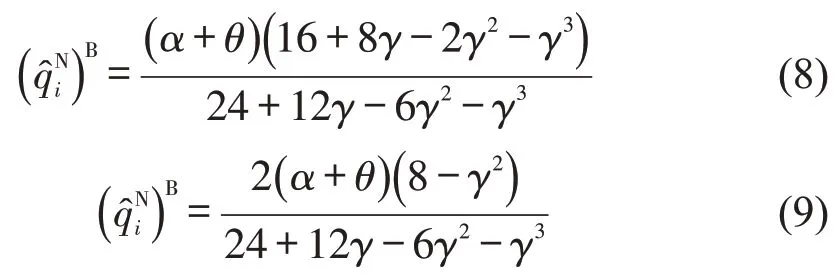

政府的社会福利为
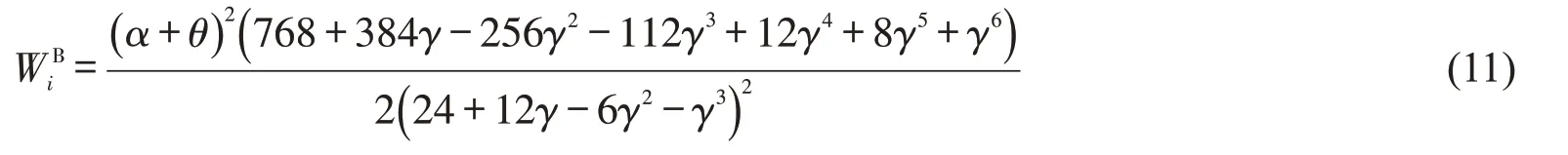
1.2 情形F平台公司合作
两个平台公司选择在竞争市场中合作,资源整合追求共同利润最大化。平台公司合作成为更大的服务提供商,将吸引更多的托运人。在该情形下,两个平台公司通过联合决策发送量以实现总利润最大化。平台公司联合决策发送量的利润函数为

分别对发送量,求导,并验证海塞矩阵负定,求出最优响应函数为

将式(13)和式(14)代入式(4),并对Wi求导,得到补贴的最优解为


将上述结果分别代入式(4)和式(5),得到平台公司利润为
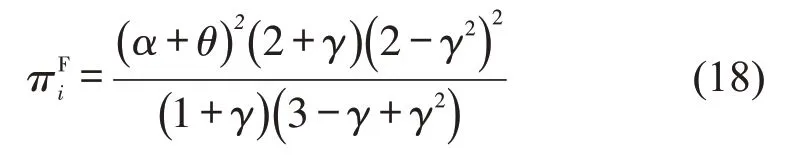
政府考虑的社会福利为
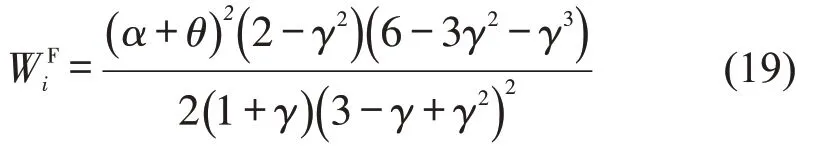
1.3 情形G政府牵头合作
政府层面的合作是由政府牵头,共建区域城市一体化发展,共同推进两地对外开放通道。例如,重庆与成都开行的中欧班列是国内货值最大、辐射范围最广、产业带动最强的两大中欧班列[12]。在中央政府的支持下,两地积极构建“双城经济圈”,在“通道口岸互联”方面开展深入合作,共同提升中欧班列市场化运营水平,共享运力、市场与政策信息。两地政府通过联合决策制定补贴策略,平台公司通过联合决策发送量实现总利润最大化。
平台公司联合决策发送量qMi,的利润函数为

两地政府联合决策补贴si的社会福利函数为

求解方法同上,得到最优结果为
本次工程新建八字墙、涵洞与闸井位于老涵洞首端,新建闸井通过新建涵洞与老涵洞相连。新建涵洞为矩形箱涵,闸井两侧做混凝土板护坡,总长度29.2m,护坡混凝土面板采用C20F200现浇混凝土板。建筑工程部分详细概算如表1,得到建筑工程部分总概算91.59万元。

将上述结果分别代入式(6)和式(7),得到平台公司的总利润为

两地城市的总社会福利为

进一步讨论情形G下,两地方政府对补贴的最优分配。假设两地方政府在选择合作时对于总补贴的分配比例分别为λ和1-λ(0<λ <1),即对平台公司i的补贴总额占总补贴的比例为λ,平台公司j的补贴总额占总补贴的比例为1-λ。只有当合作的社会福利大于竞争的社会福利时,两地方政府才会合作,即WiG≥WiB。将上述求得的政府补贴和平台公司发送量的均衡解分别代入后得到

由此可以判断地方政府i选择合作的充要条件是λ≥Fi,其中Fi为

同样,地方政府j选择合作的充要条件为1-λ≥Fj。因此,地方政府在选择合作时补贴分配比例的最优解在区间[Fi,1-Fj] 。
2 竞争与合作分析
比较分析上述3种情形下的结果,探索中欧班列哪种合作程度对平台公司和地方城市最有利,对平台公司最有利还是对整个社会福利更有利。
命题1 比较3 种情形下平台公司在两个市场中的需求可以得到
(b)在外地市场中,当0.36<γ≤0.94 时,;反之,
命题1说明,两地中欧班列的合作程度对平台公司的本地需求和竞争需求有不同的影响。本地市场中:平台公司自主选择合作策略,本地需求会得到更大的提升,这是因为在其他条件不变的情况下,与基本模型相比,合作比竞争有利;与政府牵头下的合作策略相比,平台公司自主选择合作策略对本地需求的提升更大,这其中有政府合作制定补贴政策的影响,将在下文中讨论。外地市场中,3种情形对需求的影响受到竞争程度的影响。当竞争强度γ∈(0.36,0.94]时,两种形式的合作使外地市场需求下降;反之,平台公司自主合作会增加外地市场需求,政府牵头合作会降低外地市场需求。总的来说,平台公司自主选择合作策略时总需求是最大的。 3 种情形下,总需求的对比为:
命题2说明,两种形式的合作都会提升平台公司的利润。相比而言,平台公司自主选择合作比在政府牵头共同制定补贴政策下合作所得到的利润更高。对于平台公司而言,在政府牵头下的合作并不是最优的。所以企业若是追求更高的利润和更大的集装箱需求量,平台公司应主动与竞争者寻求合作。
政府在考虑社会福利最大化的情况下,平台公司主动合作和政府牵头合作都会导致补贴额上涨。对于企业来说,依然是优先选择主动寻求合作;对于政府来说,政府牵头带动平台公司合作可以提供相对较少的补贴额。
命题4 说明,相比较而言,政府牵头合作下得到的社会福利更高。与命题3综合考虑,对于政府而言,选择牵头合作会带来更大的社会福利,同时补贴值与平台公司合作相比也相对较低。因此,对于政府来说,最优选择是牵头合作。
3 数值分析
通过比较发现,3 种情形下政府与平台公司的选择策略有所不同,为更直观地表现这种差异,用数值模拟进行比较,假设α=1 ,θ=0.05 ,结果如图2~图4所示。

图2 总需求Fig.2 Total demand
从图2可以看出,竞争强度系数较小时,3种情形下平台公司的需求量大小相接近,说明竞争较小时,平台公司选择合作的动力较小;竞争强度系数越大,3种情形下总需求的差距越大,说明合作策略对平台公司总需求量的影响越大。
从图3可直观看出,竞争强度系数越大,合作策略带来的收益越大。整体来看,竞争状态下平台公司的利润始终小于合作时的利润。

图3 平台公司的利润Fig.3 Agent firms'profits
图4表明政府牵头合作下的社会福利始终是最大的。随竞争系数增大,平台公司的合作对社会福利的负面影响也增大。

图4 社会福利Fig.4 Social welfare
两个平台公司的竞争越激烈,即竞争强度系数越大时,平台公司与政府的合作决策对结果影响越大,则对合作的要求越高;反之,两个平台公司间竞争较小,即竞争强度系数较小时,合作决策对结果产生的影响亦较小,平台公司或地方政府寻求合作的动力就越小。由结果可以得出,当市场竞争较激烈时,两个平台公司应主动寻求合作,得到更大的利润。
4 结论
中欧班列在高质量发展的过程中,主动与竞争对手合作将缓和恶性竞争,减少因“价格战”带来的资源浪费等不利影响。本文考虑了由地方政府、平台公司构成的双层竞合结构,分析比较了完全竞争、平台公司合作、政府牵头合作3种情形下的均衡结果以及决策者的最优选择。研究结果表明,政府牵头合作将有利于提高社会福利,但这种合作模式对于平台公司来说却不是最优的,平台公司更倾向于选择主动与竞争激烈的对手进行合作。本文的贡献在于根据中欧班列发展的实际现状,在同时考虑地方政府与平台公司决策的情况下,构建模型量化分析合作与竞争的利弊。然而值得注意的是,依靠政府补贴来维持发展平台公司的可持续发展并不是长久之计。政府补贴在中欧班列运营初期起到了至关重要的作用,但是经过8年的发展,补贴值依然居高不下导致平台公司之间恶性竞争。中欧班列依赖补贴的主要原因是货源不足,平均成本高、运营效率低。如果可以获得充足的货源,提高集装箱发送量,形成规模经济,就会降低中欧班列的平均运行成本,从而降低对政府补贴的依赖,才更有利于政府对补贴退坡政策的实施。因此,平台公司间的合作也是推动政府补贴政策退出有效路径。
2020年新冠疫情的爆发严重影响了国际贸易和世界物流与交通运输发展,中欧班列成为疫情下维持国际贸易联通的重要支撑,故中欧班列的未来发展成为关注的焦点。本文丰富了关于中欧班列竞争与合作关系的理论研究,对于中欧班列市场化发展,为相关部门与平台公司提供了决策依据。
