基于热电类比原理的变压器负载能力评估模型

周则儒，陈斌，李应光，霍伟锋 ，韦乾龙，唐文虎，钱瞳

(1. 广东电网有限责任公司东莞供电局，广东 东莞 523000；2．华南理工大学 电力学院，广东 广州 510641)

分布式能源以及大量的动态负荷(如电动汽车等)接入配电网，导致变压器负载率一直居高不下。大型油浸式电力变压器承担着电压变换、电能传输的作用，因突发事件或者负荷过载导致的变压器故障，将直接影响电网的正常运行[1-3]。油浸式电力变压器在过负载运行时，温度会急速升高，降低变压器绝缘强度，进而影响变压器的使用寿命。因此，对变压器负载能力进行有效的评估，在降低电网过载风险、提升负荷潜力以及提升电网可靠性等方面有重要价值[4]。

目前，国内外众多学者在变压器负载能力评估方面开展了大量的研究工作。根据GB/T 1094.7—2008《电力变压器 第7部分：油浸式电力变压器负载导则》(以下简称“导则”)规定，负载率不超过铭牌额定值的200%[5]。文献[6]提出了一种基于改进热点温度以及考虑设备故障率和经济性等多因素的变压器过负荷性能评价模型，适用于短期过负载。文献[7]建立了一种考虑变压器健康指数的故障率模型。文献[8]提出了考虑变压器寿命损失风险以及故障风险的过载评估方法，分析结果证明该方法具有很好的经济效益。文献[9]提出了考虑热点温度、顶层油温和相对寿命的变压器负载能力评估模型，通过实验证明了该模型在提升变压器负载能力方面的应用效果。文献[10]提出了一种基于改进支持向量机的变压器热点温度预测方法，以环境温度、顶层油温和负载电流作为特征值，该方法对变压器热点温度的预测精度达到90%。文献[11]利用扩展卡尔曼滤波器对变压器运行过程中的简单等效热回路参数进行拟合，同时引入过载因子，提升了热点温度的预测精度。文献[12]通过设置环境温度、初始负荷、过载倍数以及温升为变压器过载能力计算的约束条件，在1台500 kV变压器上进行了负载能力测试，提升了变压器的负载能力。文献[13]则通过分析负荷、环境温度以及用户电量，基于统计学理论，研究了变压器的负载能力和上述特征变量之间的相关性，结果表明变压器的负载能力与环境温度以及地区用电量有密切关系。文献[14]通过研究48台电力变压器的负载状态，证明以套管和分接开关为主的变压器辅助装置的容量等级是影响变压器负载能力的重要因素。

通过对上述研究工作总结可知，热点温度的精确预测和约束条件的建立是影响其负载能力评估的重要因素。但是上述研究忽略了日照辐射等典型环境因素，而且在负载能力评估时没有全面考虑辅助设备容量等级和故障率的约束。基于此，本文的主要研究工作如下：

a)基于热电类比原理，建立考虑日照辐射的温度估算模型；

b)综合考虑顶层油温、热点温度、相对寿命损失、故障率以及辅助装置容量约束，建立变压器负载能力评估模型。

1 基于热电类比原理的温度估算模型

1.1 变压器热源功率

在Tang等人提出的唐-油温模型的基础上[15]，本文通过引入日照辐射功率，修正了原有模型的热源。变压器的热源功率包括内部热源功率和日照辐射功率，即

Pall=Pi+Psun.

(1)

式中：Pall为热源总功率；Pi为内部热源功率；Psun为日照辐射功率。

根据物理学理论，物体的日照辐射量受到多种因素影响。本文中日照辐射功率

Psun=αφSpsun.

(2)

式中：α为日照辐射吸收系数；S为有效辐射面积；psun为单位面积上的日照辐射功率[16]；φ为有效辐射面积系数，与太阳辐射角度有关。

本文对φ进行拟合，即

(3)

式中j为当前时段(将1 d分为24个时段，每个时段为1 h)。

1.2 热导的修正

变压器内部产生的热量导致油黏度的值发生改变，因此本文重新修正了热导。根据热传导理论，变压器的非线性热导与很多物理参数相关，如表面几何尺寸以及各介质参数等[17-19]。本文在考虑多种因素后，将非线性热导修正为

(4)

式中：G为非线性热导；a、b为待定系数；Δθoil为油温变化值；μ为油黏度。

油黏度μ可以表示为

(5)

因此热导矩阵

(6)

式(5)、(6)中：μ1、μ2为不同油温节点之间油的油黏度；Gi(i=1, 2, 3)为油温节点之间的热导；θ1、θ2、θ3分别为模型输出的热点温度、顶层油温和底层油温；θamb为环境温度；ai、bi(i=1, 2, 3)为待优化的参数。

1.3 热容的计算

变压器的热容只与对应的温升节点有关，因此对于变压器某一确定部分而言，热容[20]

C=cpρV，

(7)

式中cp和ρ分别为变压器某一部分的比热容和密度，V为相应的体积。

1.4 温度估算模型

为了使变压器的热电类比模型可以更好地反映出环境温度变化的影响以及变压器实际运行中各个油温节点，本文建立了如图1所示的变压器温度估算模型[15]，其中，C1为变压器内部各个结构组成的等效热容，C2和C3为每个油温节点相对环境温度的等效热容。

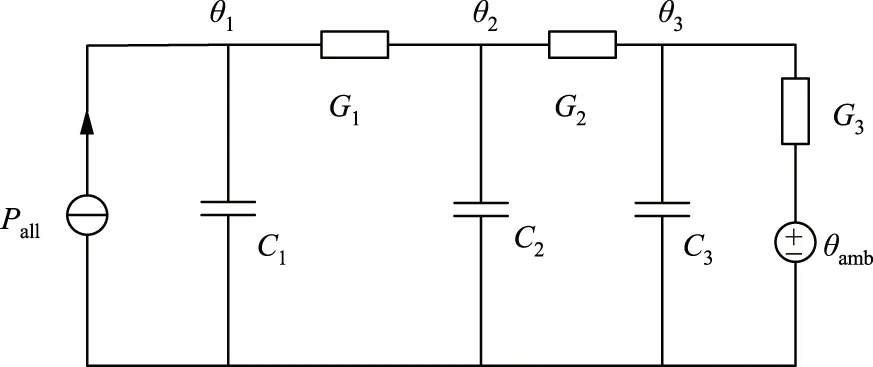
图1 变压器温度估算模型Fig.1 Transformer temperature estimation model

根据图1，利用电路原理，可以得到温度估算模型的数学表达式为

(8)

式中t为运行时间。

1.5 案例测试

本文选取1台冷却方式为ONAN/OFAF的50 MVA、121 kV/10 kV油浸式电力变压器，其空载损耗、负载损耗、杂散损耗分别为27.59 kW、175.8 kW、26.5 kW。

变压器运行较长时间后，热参数发生了变化，仅依靠变压器的出厂数据来确定参数是不可取的。本文采取遗传算法，结合变压器的实时数据，对热参数(ai、bi、Ci)进行优化。

对于本文提出的温度估算模型，适应度函数为：

(9)

式中：ΔθHST(k)、ΔθTOT(k)、ΔθBOT(k)分别为热点温度、顶层油温、底层油温计算值与实时测量值之间的误差，各误差的平方和分别用fHST、fTOT、fBOT表示；θMBOT(k)、θMTOT(k)、θMHST(k)分别为实时测量的底层油温、顶层油温、热点温度；N为监测样本的个数。

选取夏季东莞供电局宝石变电站平均单位日照辐射功率为200 W/m2的1 440组实时监测数据，其中t=1 000 min至t=1 288 min这段时间冷却器处于打开状态，其余时间冷却器处于关闭状态。利用以上优化的热参数构建新模型，将其油温计算值与唐-油温模型、导则方法的油温计算值，以及实时测量油温值进行对比，结果如图2和图3所示。

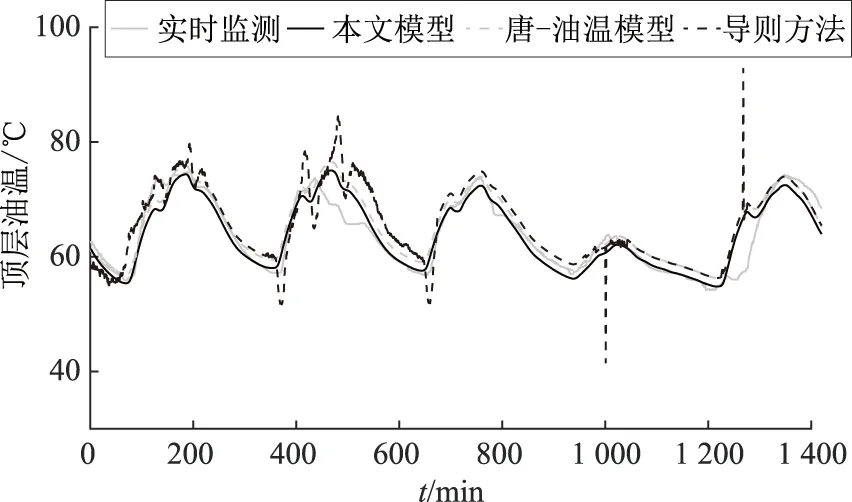
图2 顶层油温计算值与实测值的对比Fig.2 Comparisons between calculation value and measured value of top oil temperature

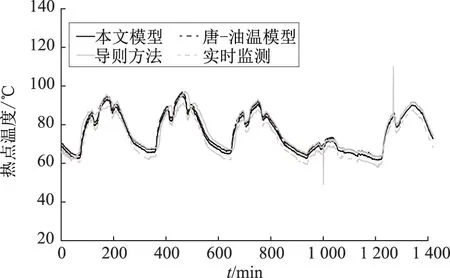
图3 热点温度计算值与实测值的对比Fig.3 Comparisons between calculation value and measured value of hot-spot temperature

t=1 000 min时冷却器突然打开，由图2和图3可以看出：导则方法没有考虑到变压器油黏度的变化，导致油温计算值发生突变，产生尖峰，引起很大的误差；而本文模型考虑了油黏度的变化，避免了变压器在冷却器切换时的响应不足。本文用均方误差来衡量多种方法计算的油温值精确度。为了分析模型计算值与实测值之间的相关性，定义相关系数

(10)

式中：yk,c为第k个计算值；yk,m为第k个实测值。

3种方法计算值相对于实测值的均方误差见表1。可以看出，本文模型得到的顶层油温和热点温度的均方误差较小，这是因为在广东等南方地区日照更加强烈，而且用户用电高峰期内变压器承担负荷较大，考虑日照辐射对变压器油温的影响后，计算结果更符合实际。

表1 3种方法计算值相对于实测值的均方误差Tab.1 Mean square errors of calculation valuess of three methods relative to measured values

3种方法计算值相对于实测值的相关系数见表2。可以看出，本文模型得到的顶层油温和热点温度与实测值之间的相关系数更接近于1，说明本文模型在考虑日照辐射热源以及变压器油黏度的变化后，计算得到的油温值较好地跟踪了实测值的变化趋势，更好地反映了变压器的热传递过程。

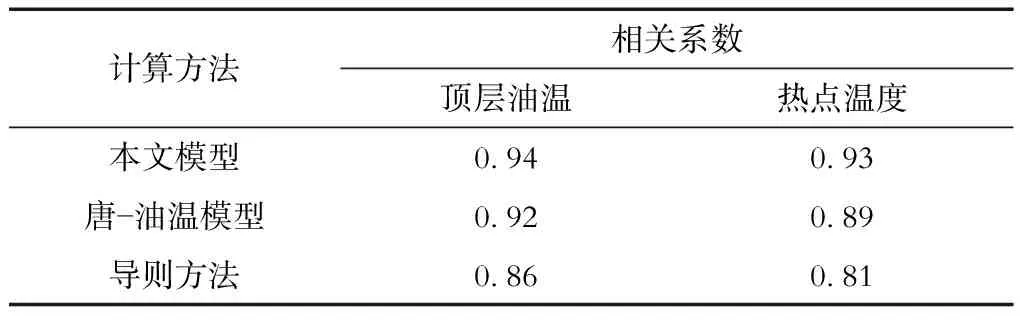
表2 3种方法计算值相对于实测值的相关系数Tab.2 Correlation coefficients of calculation values of three methods relative to measured values

对于日照辐射强度不高的地区，日照辐射热源影响较小，此时模型等价为文献[9]中提出的改进热电类比模型，此时的模型仍然有较高的精度。

2 负载能力评估模型

为了避免变压器由于过负荷导致的故障，本文用新的温度估算模型对不同类型的负载进行负载能力评估。

如果变压器采用的是非热改性绝缘纸，则定义其相对老化率

v=2({θHST}℃-98)/6,

(11)

式中θHST为热点温度。

实际运行时，负荷和环境温度在实时变化，其相对寿命损失

(12)

式中t1、t2分别为运行起始时间和结束时间。

变压器的故障率也是评估变压器负载能力的重要因素，在过载运行情况下，变压器的绝缘强度及性能出现下降。故障率与变压器的负载率以及热点温度有关，为了保证过载运行的安全性，对于短期急救负载，需要考虑故障率这一重要因素。变压器故障率λ计算公式为[7]：

(13)

(14)

式(13)、(14)中：β和m为蒙特卡洛拟合参数；μH为健康指数；T为等效运行时间；A和B为计算变压器出厂寿命损失值的经验参数。在本文中，β=4.265 9，m=-3.677 1，T=180 000 h，A=1.763 4×10-12，B=15 000。

变压器负载类型包括周期性负载、长期急救负载、短期急救负载[8]。在不同的负载类型下，变压器的负载能力影响因素也呈现出不同的特征。

2.1 正常周期性负载能力评估

当变压器处于正常周期性负载运行时，如果环境温度过高或者负载电流过大，会影响变压器的使用寿命[21-22]，在正常周期性负载时，暂不考虑故障率这一因素。此时，正常周期性负载能力评估模型为：

(15)

式中：K为变压器的负载率；θTOT为顶层油温；Kl为辅助设备容量等级限值，设置为Kl=1.2[14]。

不同温度时，在上述约束条件下，本文模型与导则方法对变压器的正常周期性负载能力评估结果见表3(括号内数值为导则方法计算结果，下同)。

表3 正常周期性负载能力评估结果Tab.3 Assessment results of normal periodic load capacity

设置环境温度为20 ℃，采用本文模型对变压器进行周期性负载能力评估，得到最大顶层油温、最大热点温度、相对寿命损失随负载率的变化情况如图4所示。

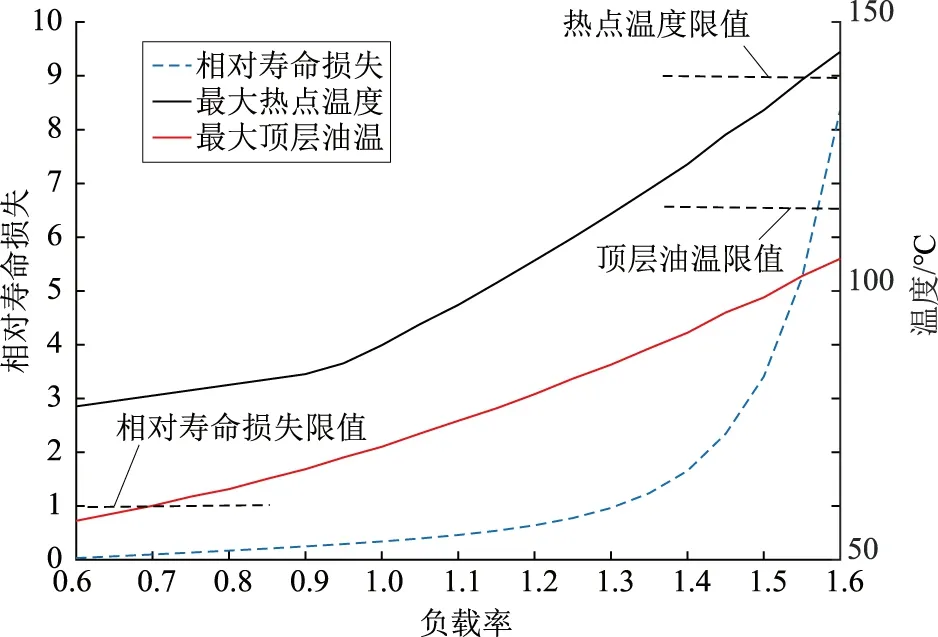
图4 最大顶层油温、最大热点温度、相对寿命损失随负载率的变化情况Fig.4 Curves of the maximum top oil temperature, maximum hot-spot temperature and relative daily loss of life varying with load changes

从表3可以看出，在环境温度较低(例如10 ℃)时，2种方法计算的最大顶层油温、最大热点温度、相对寿命损失均未超过限值，但是负载率却已经达到1.2。这个结果说明，环境温度较低时，影响周期性负载能力的主要因素是辅助设备容量等级。

对比2种计算方法，在环境温度为30 ℃时，导则方法和本文模型计算得到的最大顶层油温、最大热点温度均未超过限值时，相对寿命损失已经达到0.98和0.96，同时本文模型的负载率可以达到1.05，而导则方法的最大负载率仅为0.85。这个结果说明在环境温度较高时，本文模型更有利于提高变压器负载能力，并且此时影响正常周期性负载能力的主要因素是相对寿命损失。

2.2 长期急救负载能力评估

当变压器处于长期急救负载时，此时变压器牺牲一部分寿命来维持运行，即允许变压器的相对寿命损失大于1。同样地，长期性急救负载时暂不考虑故障率。因此，长期急救负载能力评估模型为：

(16)

在上述约束条件下，本文模型对长期急救负载能力的评估结果见表4。

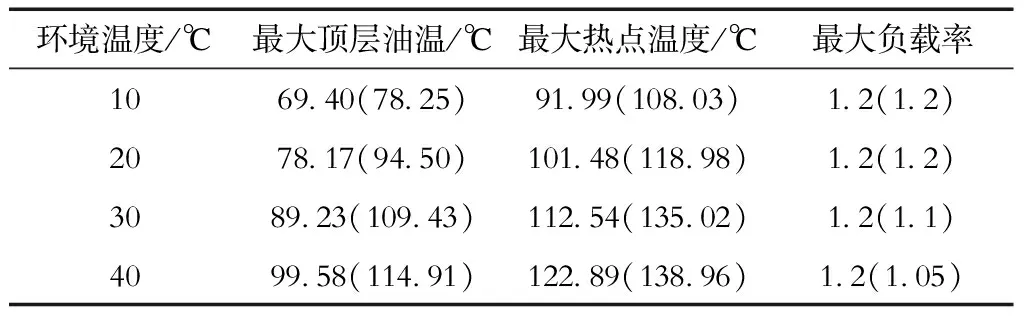
表4 长期急救负载能力评估结果Tab.4 Assessment results of long-term emergency load capacity

由表4可知，环境温度较低时，在牺牲一部分变压器的寿命损失后，在变压器的顶层油温和热点温度还没达到约束值时，2种方法的最大负载率已经达到了辅助设备容量等级限值。这个结果说明环境温度较低时，影响长期急救负载能力的主要因素是辅助设备容量等级。环境温度较高时(例如30 ℃)，导则方法得到的最大负载率为1.1，本文模型得到的最大负载率为1.2，同样说明本文模型提升了变压器最大负载能力，并且此时导则方法计算的顶层油温和热点温度均达到限值，这说明影响长期性负载能力的主要因素是顶层油温和热点温度。

2.3 短期急救负载能力评估

当变压器处于短期急救负载时，持续时间比较短。但是此时变压器热点温度过高，影响了其绝缘性能，所以此时可忽略相对寿命损失以及辅助设备容量等级的限制。由于短期急救负载发生时负载率过大，变压器处于暂态运行，所以不仅需要关注变压器所能承担的最大热点温度、最大负载率、故障率，还需要关注变压器的最长运行时间。因此，短期急救负载能力评估模型为：

(17)

设定起始负载率为0.63倍额定负载率，本文的变压器故障率上限λ1为2.79×10-6次/(台·h)[7]。每分钟增加负载率0.05倍，对变压器负载能力进行评估，结果见表5。

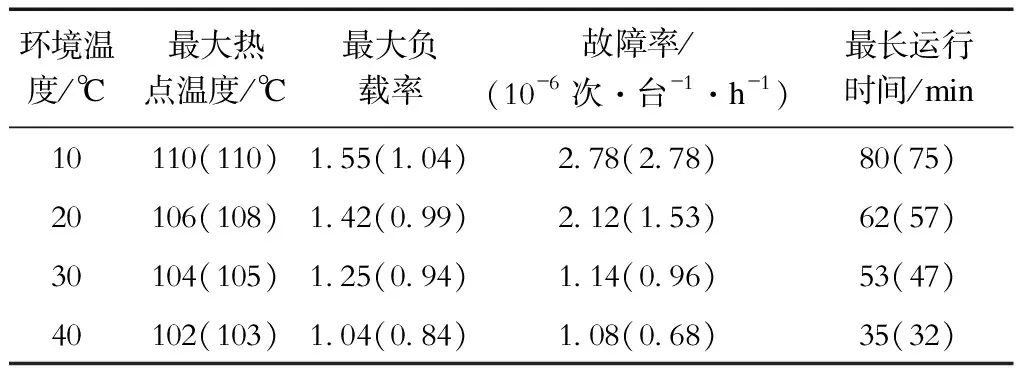
表5 短期急救负载能力评估结果Tab.5 Assessment results of short-term emergency load capacity

由表5可知，环境温度为10 ℃时变压器的最长运行时间为40 ℃时的2倍多，这说明短期急救负载能力会随着环境温度的升高而降低。同时可以看出，无论环境温度的值多大，在热点温度未达到约束值时，故障率均已接近约束值，这说明短期急救负载的主要影响因素是环境温度与故障率。

同时由表5可知，对于短期急救负载，在环境温度与故障率的约束下，本文模型相比导则方法提升了变压器最大负载能力。

3 结束语

本文基于热电类比原理，加入日照辐射作为新的热源，同时考虑温度对变压器油黏度的影响，提出了新的温度估算模型。分析结果证明本文模型相比唐-油温模型、导则方法计算精度更高，更能反映变压器内部的热传递过程。考虑顶层油温、热点温度、相对寿命损失、故障率以及辅助设备容量等级等约束条件，建立负载能力评估模型，并且对不同类型的负载进行了评估。结果证明：环境温度较低时，辅助设备容量等级是变压器正常周期性负载能力的主要影响因素；环境温度较高时，相对寿命损失是变压器正常周期性负载能力的主要影响因素；辅助设备容量等级是影响长期急救负载能力的主要因素；环境温度和故障率是影响短期急救负载能力的主要因素；对于3种不同类型负载，本文模型相比导则方法均提升了变压器的负载能力。

需要指出的是，本文的负载能力评估模型未考虑变压器的经济性等约束条件，但对于挖掘变压器的负载能力仍然具有重要指导意义。