智能电网中考虑温积效应的OSVR负荷预测

2021-04-28任萌高小征

广东电力 2021年4期

任萌，高小征

(广东电网有限责任公司梅州供电局，广东梅州 514000)

负荷预测是能量管理系统(energy management system，EMS)的一个关键功能，是电力系统经济调度中的一项重要内容[1]。负荷预测不仅是确保电力系统安全经济运行的必要前提，也是制订电力市场交易计划的基础[2-3]。随着国家大力倡导绿色能源，以及节能减排方针的提出，对负荷预测精度的要求越来越高。然而，气候等外在因素的随机性和多变性给预测工作带来高难度的挑战。

预测的本质是通过学习历史样本所隐含的规律特征，进而推测出未来的发展趋势[4]。文献[5-8]应用群智能优化系统改进支持向量机、神经网络等算法的拟合能力，建立离线式组合预测模型。但离线预测模型具有时间滞后性，不能够快速、实时地反映最新数据样本的变化情况，导致预测模型会随时间退化，甚至失效。电力系统运行状况以及环境数据瞬息万变[9]，因此预测过程也应是时变性的，为了持续保持模型的优良性能，需要建立在线预测模型，实时校正模型参数。

随着智能电网技术的发展和普及，实时、便捷的智能仪表给预测人员提供了大量流水式数据，这为负荷系统实现在线预测提供了契机[10]。在线预测方法最大的特点就是模型训练过程与数据采集过程几乎同步进行。当有新样本添加时，在线系统自动判断新数据的属性，进而采取相应的算法机制进行跟踪学习，动态地拟合当前负荷曲线趋势，保证模型的持续有效性[11]。与离线预测系统不一样，为了节省时间成本与内存成本，在线预测系统无需重复学习旧数据，而是在原有模型的基础上，通过学习新样本来修正模型参数[12]。

气温是负荷预测中的重要变量，负荷曲线除了与当前气温有关，还受到过去几个时段乃至过去几日的气温影响[13-14]，这就是温积效应[15]。文献[16]直接将待预测日的天气预报气温作为模型输入量之一，而忽略了温积效应对负荷曲线的影响。文献[17-19]根据经验数据，简单地将前几日的气温进行加权输入，缺乏理论支撑。

本文基于支持向量回归(support vector regression，SVR)原理[20-21]，结合卡罗需-库恩-塔克(Karush-Kuhn-Tucker，KKT)条件[22-23]，运用递增算法建立在线支持向量回归(online support vector regression，OSVR)预测模型。同时，考虑到温积效应对负荷输出有着不可忽视的影响，本文运用Fisher信息(FI)[24]理论处理气温数据。FI理论是度量系统稳定性的有效方法，能够检测系统状态及其变化情况[25]。FI可以挖掘温度数据序列的规律特征，进而解决温积效应对负荷预测系统的影响，从而避免人为处理温积效应的主观随意性。

1 OVSR原理

不同于离线SVR模型，OSVR采用递增算法进行模型校正[26]。每次添加1个新样本时，OSVR只根据该数据进行学习，而无需结合旧样本重新训练，因此，OSVR能够根据现场不断传来的数据流实时调整模型参数。

给定1组数据集{(xi,yi)︱i=1，2，…，N}，其中xi为输入向量，yi为对应的真实值，N为数据集中样本个数。利用函数φ将样本映射至更高维空间并进行线性回归，回归函数[21]

f(x)=ωTφ(x)+b.

(1)

式中：ω为权重向量；b为偏移量。

根据结构风险最小化准则，构建最小化目标函数

(2)

式中ε为不敏感系数。

回归估计函数

(3)

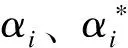
(4)

其中δ为核宽度。

根据式(3)、(4)可构造回归方程

(5)

预测误差函数

h(xj)=f(xj)-yj=

(6)

根据KKT条件可以将训练数据集分为误差支持向量集E、边界支持向量集S、剩余样本集R，

(7)

(8)

(9)

式(7)—(9)中C为分类界值。

OSVR的核心是保证样本集始终满足KKT条件。当添加新的样本(xc，yc)时，OSVR采用递增算法校正模型参数，递增算法的基本思想是逐步更新样本xc所对应的偏差系数θc，直至满足KKT条件。

对于新样本(xc，yc)，首先需要判断其所属数据集。若xc∈R，则原SVR模型参数θi、b无需更变，迭代结束。

若xc∈E或xc∈S时，不断改变θc、θi、b以满足KKT条件[22]。有2种情况：

a)xc∈S时，偏差系数递增量Δθc最小，则h(xc)从h(xc)<-ε变更为h(xc)=-ε，Δθc=-h(xc)-ε，此次迭代结束；

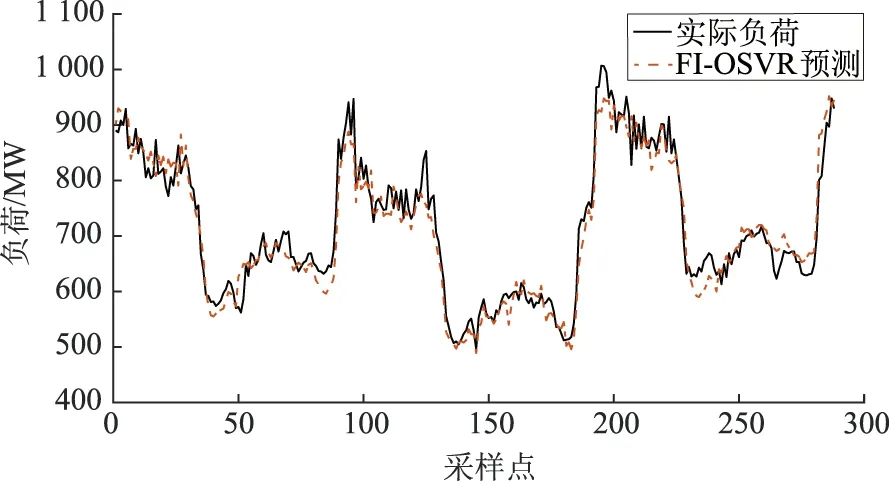
b)xc∈E时，θc从θc

结合式(5)、(6)可得

Δh(xi)=k(xi,xc)Δθc+

(10)

递增算法实时监察追踪训练集的样本，追踪分为5种情况，具体过程可参考文献[12]。

2 FI在预测过程中的应用

2.1 FI的基本原理

FI技术是基于统计学理论而提出的一种定量评测系统稳定性的方法，其表达式为[27]

(11)

式中：I为系统稳定性的度量值；s为系统状态变量，本文中表示气温变量；P(s)为概率密度分布函数。一般大多数系统常常处于非常稳定(此时P(s)呈尖锐形状，其导数趋于无穷大，对应I=∞)与非常不稳定(密度函数P(s)的导数趋于0，对应I=0)之间，因此采用式(11)度量系统稳定性是合理的。为了方便计算，经常使用P(s)的某个量的相似强度函数进行替代，因此可令P(s)=q2(s)，代入式(11)得：

(12)

对于离散型的气候数据序列，使用差分代替式(11)中的微分，即ds和dq(s)可分别用(sa-sa-1)和(qa-qa-1)来代替，其中a为状态序列号。考虑到2个状态变量之差sa-sa-1=1，式(12)可简化为

(13)

式中A为状态总数。

系统的概率密度分布计算是FI计算的关键[25]。假设离散数据序列集为G={g(k),k=1,…,K}，K为序列总长度，在该序列上构造一个滑动窗

W(m,w,τ)=

{g(k),k=1+mτ,…,w+mτ}.

(14)

式中：w、τ分别为窗宽和滑动因子，m=1，2，…，M，M=(K-w)/τ。

每个滑动窗的所有序列可划分为H个区间，即

(15)

式中Zh=(Sh-1，Sh)，这里的Sh表示区间边界。由此可见，g(k)∈W(m,w,δ)属于区间Zh的概率p(Zh)可表示为g(k)∈W(m,w,τ)落入区间Zh的个数与窗口W中总的数据数的比值，即

(16)

式中：lzh为属于区间Zh的数据个数；L为滑动窗口中总的数据个数。

2.2 温积效应的FI处理法

众多气候因素中，气温对电力系统负荷的影响最大，而过去时段的气温数据对当前的负荷输出也会产生较大的累积效应。可计算过去时段气温数据序列的FI值作为权重，对当前气象变量进行加权乘积，从而反映温积效应对电力当前负荷输出的影响。温积效应不仅体现在当日内，持续多日的高温或低温现象也会导致负荷出现异常变化，即多日温积效应。

根据经验，时间上越靠近最近时刻的气温数据，对当前负荷输出影响越明显，基于此，以智能电网15 min分辨率采样的数据为例，构建FI的窗口数据{Xd,t，Xd,t-1，…，Xd,t-11}、{Xd-1,t，Xd-1,t-1，…，Xd-1,t-7}、{Xd-2,t，Xd-2,t-1，…，Xd-2,t-3}，3个部分分别表示预测当日当前时刻前3 h内12个采样点(下标d、t分别表示当日、当前时刻，以此类推)、前1日当前时刻前2 h内8个采样点、前2日当前时刻前1 h内4个气象采样点，即数据窗共24个数据。这种“近大远小”的组合方式能更加合理、全面地表征气候因素对负荷输出的累计效应。

3 实例分析

在智能电网的实时数据流环境中，在线预测模型根据新增样本及时调整校正模型参数，并实时预测下一时刻的负荷值。本案例的数据(包括负荷、气温值)采集跨度和预测时间尺度为15 min(超短期预测)。

3.1 模型输入量设置

负荷预测精度除了与模型参数、数据处理方法等紧密关联，模型输入量的设计对预测结果也会产生显著影响。考虑到负荷样本、气温、日期类型等与电力负荷输出曲线具有较大的关联度，因此设计15个OSVR预测模型输入量，见表1。

FI-OSVR预测模型采用2.2节FI技术对气温数据进行FI处理。此时，气温输入量将降维为1个气温特征量，即FI-OSVR预测模型输入量由表1中的15个减少为11个，见表2。因此，引入FI技术，既能充分考虑温积效应对负荷的影响，又可以简化算法规模和预测模型。

表1 OSVR预测模型的输入量Tab.1 Inputs of OSVR model

表2 FI-OSVR预测模型的输入量Tab.2 Inputs of FI-OSVR model

在传统的离线SVR预测模型中，假如训练样本库添加新数据，需要结合全部新、旧样本数据重新进行模型训练。显然，这种从头开始训练的模式在实时数据流的智能电网中不适用。离线预测模型的训练样本库一般具有滞后性，传统的SVR模型习惯采用前一日的负荷数据、上周当日数据、日期类型和天气预报数据作为预测输入量。作为FI-OSVR的对比模型，本文仍然采用FI方法对离线SVR模型的气温数据进行处理，即构建FI-SVR对比模型。

3.2 仿真分析

基于MATLAB软件平台，采用某市2017年5月—9月采集的数据进行试验，样本采集分辨率为15 min，以2017年9月15日—17日的288个数据作为测试样本，对比FI-OSVR、OSVR和FI-SVR这3种预测模型的仿真结果。由于该地区重工业较多，因此凌晨低电价时段(如0—35采样点)属于电力负荷高峰期。

模型输入量数据类型不一样，数值差异较大，因此需要进行归一化处理，归一化公式为

(17)

式中：Vn、vn分别为归一化前、后的数据；Vmax、Vmin分别为输入量中的最大值和最小值。

图1—图3分别为FI-OSVR、OSVR和FI-SVR模型的仿真结果，图4—图6分别为相应的误差针图。

图1 FI-OSVR模型的预测结果Fig.1 Prediction results of FI-OSVR model

图2 OSVR模型的预测结果Fig.2 Prediction results of OSVR model

图3 FI-SVR模型的预测结果Fig.3 Prediction results of FI-SVR model

图4 FI-OSVR模型的预测误差针图Fig.4 Needle plot of FI-OSVR model prediction errors

图5 OSVR模型的预测误差针图Fig.5 Needle plot of OSVR model prediction errors

图6 FI-SVR模型的预测误差针图Fig.6 Needle plot of FI-SVR model prediction errors

如图1—图3所示，3个模型的预测曲线基本都能够较好地拟合实际负荷趋势，初步验证了SVR技术在负荷预测中的可行性。下面进一步对比分析FI-OSVR和OSVR模型，以及FI-OSVR和FI-SVR模型的预测结果。

对比图1、2，以及图4、5可知，在中午、下午时段(如45—70采样点)，采用了FI技术的FI-OSVR模型的曲线拟合能力明显比OSVR模型好。这是由于此时段属于环境气温持续攀升的高温期，温积效应较为明显，而FI-OSVR模型能够准确捕捉温积效应对电力负荷的影响。这个结果验证了FI技术在负荷预测中的实用性。

对比图1、3，以及图4、6可知，在3 d的测试中，相较于离线模型FI-SVR，FI-OSVR模型始终以较小且更稳定的误差跟踪实际负荷输出曲线。这是因为FI-OSVR模型采用在线建模方式，实时校正模型参数，从而能够及时反映系统运行状况及环境变化情况。这个结果说明在线模型具有更好的动态预测能力。

为了更为直观对比FI-OSVR、OSVR和FI-SVR这3种模型的预测精度，从2017年5月—9月中每月随机抽取2日(共10 d，960个预测时刻)进行测试，并将3个模型的误差曲线呈现在同一张图上，如图7所示。

图7 3种模型的预测误差曲线对比Fig.7 Comparisons of prediction errors of three models

图7显示FI-OSVR模型的误差曲线波动幅度明显小于OSVR模型和FI-SVR模型的误差幅度。

本文以标准均方根误差(normalized root mean square error，NRMSE)以及平均绝对百分误差(mean absolute percentage error，MAPE)定量评判各模型的预测误差，具体计算方法为：

(18)

(19)

式中：ENRMSE、EMAPE分别为NRMSE指标和MAPE指标的值；y′i为第i个预测输出值。表3为这3个预测模型的误差值。

表3 3种模型预测误差值Tab.3 Prediction errors of three models %

表3显示，FI-OSVR模型的NRMSE以及MAPE均比OSVR模型和FI-SVR模型低，OSVR模型次之，而FI-SVR模型最差。不难得出结论：FI-OSVR模型的预测能力明显优于没有考虑温积效应的在线模型OSVR和考虑温积效应的离线模型FI-SVR。

3.3 效果评价

本文所建立的FI-OSVR模型引入KKT条件，采用递增算法动态学习最新样本数据，使得模型能够较好地拟合负荷曲线。测试结果显示，FI-OSVR预测模型的NRMSE和MAPE分别为2.052%、1.462%，远低于FI-SVR模型的预测误差，说明在线模型FI-OSVR比离线模型FI-SVR的负荷预测能力更强。

FI-OSVR模型考虑了温积效应，并采用FI定量分析温度状态变化特性，而OSVR则直接将未经FI处理的温度数据输入预测模型。测试结果显示，OSVR模型的NRMSE和MAPE分别为4.175%、3.134%，均大于FI-OSVR模型的相应误差值，说明温度数据经过FI处理的FI-OSVR模型的预测效果更好。