基于电化学阻抗谱的锂离子电池等效电路模型参数辨识方法
2021-04-27李日康王学远戴海峰魏学哲
口 尧,李日康,王学远,戴海峰,魏学哲
(1.同济大学新能源汽车工程中心,上海 201804;2.同济大学电子与信息工程学院,上海 201804)
0 引言
锂离子电池以其循环寿命长、能量密度大、工作温度范围广等特点成为最重要的新能源汽车储能电源之一。随着锂离子电池应用范围的日益广泛,其能量密度也在不断提高,伴随而来的寿命和安全性问题也越来越突出。相应地,阻抗作为电池的基本属性之一,其可以反映电池内部物理和化学过程,在电池状态估计、寿命预测及故障诊断方面有着广泛的应用前景。车载阻抗在线应用流程可分为阻抗测量[1-3]、准稳态检测、参数辨识和阻抗应用。利用准稳态检测后的电化学阻抗谱可以将电池等效为由电阻、电容和电感组成的等效电路模型[4]并进行相应的参数辨识,阻抗应用则可以通过分析等效电路模型中的各阻抗成分随电池状态的变化规律来实现。以电池老化状态估计为例,Yuan等[5]发现传荷电阻随电池老化的变化十分明显,并且具有良好的抗SOC漂移的能力。Saha等[6]证明了传荷电阻、电解液电阻与电池老化间的线性关系,并以此实现了基于序列蒙特卡洛方法的电池老化状态估计。
等效电路模型参数辨识是电池BMS系统利用阻抗进行应用的必要前提。实验室中传统的阻抗谱分析手段是通过Z_view等商用软件进行离线处理,其需要实验人员多次进行手动调整,工作耗时烦琐且离线量化分析极大地限制电池阻抗的在线应用。因此,本文提出了一种无需人为干预的锂离子电池等效电路模型参数辨识方法,为阻抗谱在线进行状态估计以及寿命预测等应用提供了基础。
1 等效电路模型
本文选取的等效电路模型以及与阻抗谱各频段曲线对应关系如图1所示。
图1中,高频电感L用来模拟由于集流体和导线所带来的杂散电感影响;R0用来描述由于电解液、隔膜、电极和接触引起的欧姆电阻;CPESEI和RSEI表征电池负极上SEI膜阻抗,代表着阻抗谱上高频的半圆,其中RSEI代表着膜电阻,CPESEI代表由弥散效应引起的膜电容;CPEdl和Rct代表电极与电解液之间的界面反应阻抗,与阻抗谱上第2个半圆相对应,CPEdl用来表征由弥散效应引起的双电层电容,Rct为界面反应的传荷电阻;ZW为锂离子在固相电极中的扩散阻抗,与阻抗谱上低频段的直线相对应[7]。

图1 等效电路模型与电池阻抗谱的对应关系
根据图1选取的等效电路模型结构,可得到其阻抗为
(1)
式中,α=Rct(jωTW)PW+RWtanh[(jωTW)PW],TSEI与PSEI为常相位元件CPESEI的参数;Tdl与Pdl为常相位元件CPEdl的参数;RW代表韦伯阻抗的大小;TW与PW为韦伯阻抗元件ZW的参数。
2 等效电路模型参数辨识方法
由式(1)可知,等效电路模型表达式是一个关于阻抗测量频率的强非线性方程,而初始参数的选取对于非线性方程的求解十分重要。当初始参数选取不合适时,阻抗谱拟合容易出现不收敛现象,从而导致错误的参数辨识结果。因此,等效电路模型参数辨识方法的关键在于能够针对电池不同状态下所测量得到的阻抗谱自适应地获取合适的阻抗谱拟合初值。
阻抗谱一般呈现两圆弧、一直线的形貌特征,且各个特征成分有相对应的电路环节与之对应,这也为阻抗谱的辨识提供了基础。在阻抗谱的拟合过程中,可以首先对圆弧与直线形貌特征的部分进行局部拟合,然后将分段局部拟合的最终值作为整体拟合的初始值,从而实现对阻抗谱的参数辨识。
具体的分段局部拟合初值获取步骤如下:
a.插值获取阻抗谱与实轴的交点值作为R0的拟合初值,而由于实际过程中电池相连接的导线固定不变,因此阻抗谱中杂散电感值的大小相对固定且其数量级很小,本文设置其固定初始值为4×10-7Ω。
b.由于阻抗谱左侧圆弧的频率点分布密集,因此,从距离实轴最近的点开始间隔选取4个频率点进行左侧圆弧的局部拟合,获得CPESEI和RSEI元件初值。
c.找到圆弧部分的最高点,并选取最高点附近4个频率点数据对传荷电阻环节进行拟合,获得CPEdl和Rct元件初值。
d.找到阻抗谱的最后4个点,对直线段进行拟合获得成分ZW的初值。
具体的局部拟合初始参数获取过程如图2所示。

图2 阻抗谱拟合初始参数获取流程
需要注意的是,图2中步骤②-④中均在外部串联了一个电阻R,这是电池欧姆阻抗所带来影响的结果。由式(1)可知欧姆内阻的值在全频率范围内始终影响着电池阻抗的实部,因此欧姆内阻应该耦合至阻抗谱各个形貌特征的局部拟合过程。
根据获得的初始参数值则可以对锂离子电池电化学阻抗谱进行整体拟合求解,得到各个阻抗成分值,从而辨识拟合出等效电路模型参数。拟合方法采用非线性最小二乘Levenberg-Marquardt(LM)方法,拟合时迭代步长hlm计算公式为
(JT(x)J(x)+μI)hlm=-JT(x)e(x)
(2)
x为因变量;e(x)为拟合残差;J(x)为x的雅可比矩阵;I为单位矩阵;μ为阻尼调节因子(μ>0)。
阻尼因子μ起着调节hlm更新方式的作用,当μ非常小时,式(2)可近似为
JT(x)J(x)hlm=-JT(x)e(x)
(3)
此时hlm的更新近似于牛顿法,其具有收敛快但不稳定的特点。当μ较大时,式(2)可近似为
(4)
此时hlm的更新近似于最快下降法,其具有稳定但收敛较慢的特点。通过调整μ,LM方法将牛顿法和最快下降法结合在一起,形成了一种介于两者之间的算法,大大降低了残差陷入局部极小值的机会。
拟合过程中的残差e定义为

(5)
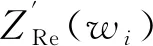
综上,电池阻抗谱等效电路模型参数辨识方法流程如图3所示。

图3 阻抗谱等效电路模型参数辨识方法流程
3 实验验证及分析
3.1 实验设计
本文以三星公司INR18650-29E电池为研究对象,电池参数如表1所示。

表1 INR18650-29E电池基本参数
为了充分验证本文提出的方法的有效性,需得到电池在不同状态下的电化学阻抗谱,综合考虑老化状态、荷电状态和温度3个影响因素,设计实验步骤如下:
a.将电池放置于25 ℃恒温箱进行老化循环25次,老化工况为先0.5C倍率充电至4.2 V,后1C倍率放电至2.5 V。
b.恒温箱温度不变,对电池进行容量标定,然后调整电池荷电状态至90%SOC。
c.恒温箱温度依次调整为40 ℃、35 ℃、25 ℃、15 ℃及5 ℃,电池在以上各个温度下进行电化学阻抗谱测量(激励电流有效值为500 mA,频率范围为10 kHz~0.01 Hz)。
d.恒温箱温度调整为25 ℃,采用1C倍率放电电流使得电池荷电状态下降20%SOC。
e.重复步骤c—d,依次测量电池荷电状态为90%SOC、70%SOC、50%SOC、30%SOC、10%SOC时,在以上各个温度值下的阻抗谱。
f.重复步骤a—e,获得电池在不同老化状态、各个温度以及荷电状态下的阻抗谱。
3.2 验证及分析
为了验证电池不同状态下的参数辨识结果,利用本文的方法对如下实验数据进行等效电路参数辨识:
a.不同循环老化次数(100、400、700)后25 ℃、70%SOC下阻抗谱,结果分别记作cycle100、cycle400和cycle700。
b.循环老化425次后不同温度(5 ℃、25 ℃、40 ℃)、90%SOC下阻抗谱,结果分别记作5 ℃、25 ℃、40 ℃。
c.循环老化425次后35 ℃、不同荷电状态(10%SOC、70%SOC、90%SOC)下阻抗谱,结果分别记作10%SOC、70%SOC、90%SOC。
将上述数据的等效电路模型参数辨识结果与商业软件Z_view所得结果进行对比计算,分别选出不同循环次数、不同温度、不同荷电状态下误差最大的3组阻抗谱参数辨识结果,其误差分布如表2所示。

表2 电路元件参数辨识误差分布 %
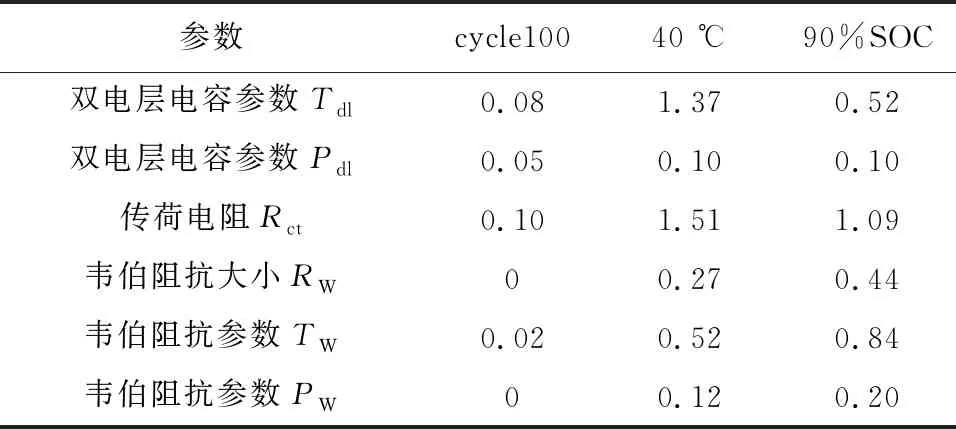
表2(续)
由表2可以观察到,除了40 ℃下SEI膜电容参数TSEI误差大于5%,其余电路元件的辨识误差均小于4%,且常用于状态估计的欧姆内阻R0、SEI膜内阻RSEI、传荷内阻Rct以及扩散阻抗ZW等阻抗成分误差均小于3%,绝对误差小于0.3 mΩ。根据图1所示的阻抗谱5个特征所对应的表征电路环节,统计特征电路环节的累积误差分布如图4所示。
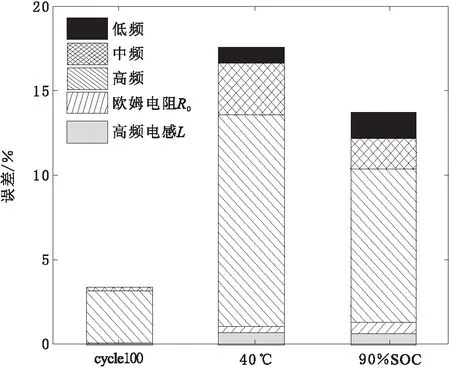
图4 电路环节参数辨识的累积误差
由表2及图4可知,电路环节累积分布的误差主要集中于SEI膜环节的3个元件成分上,其可能的原因是由于高频圆弧的频率点分布密集导致这3个元件解析值在一定范围内变化时,都会使得非线性方程求解式所代表的全局残差具有最小值。
为进一步验证本文方法的有效性,对电池处于25 ℃、70%SOC时各个循环老化下的阻抗谱进行参数辨识并与Z_view软件辨识结果对比计算,得到的参数辨识误差如图5所示。
由图5可以看出,在电池循环老化过程中,剔除第125次循环的结果,各个元件的参数辨识误差均小于2%,且在循环老化200次后该方法与Z_view辨识结果达到一致。循环老化125次与循环老化525次阻抗谱如图6所示。由图6可知,循环老化125次时,参数辨识存在较大误差可能的原因是由于前期老化过程中阻抗谱第2个圆弧不明显,且测量得到的阻抗谱噪声较大,从而影响了式(5)代表的残差值并导致拟合结果不唯一。而随着电池老化圆弧半径逐渐增大,如图6中循环老化525次的阻抗谱,从而使得噪声的影响相对地逐渐降低,拟合结果收敛于稳定值,即当电池阻抗较小时噪声的存在可能会使得该方法与Z_view软件解析结果存在偏差。
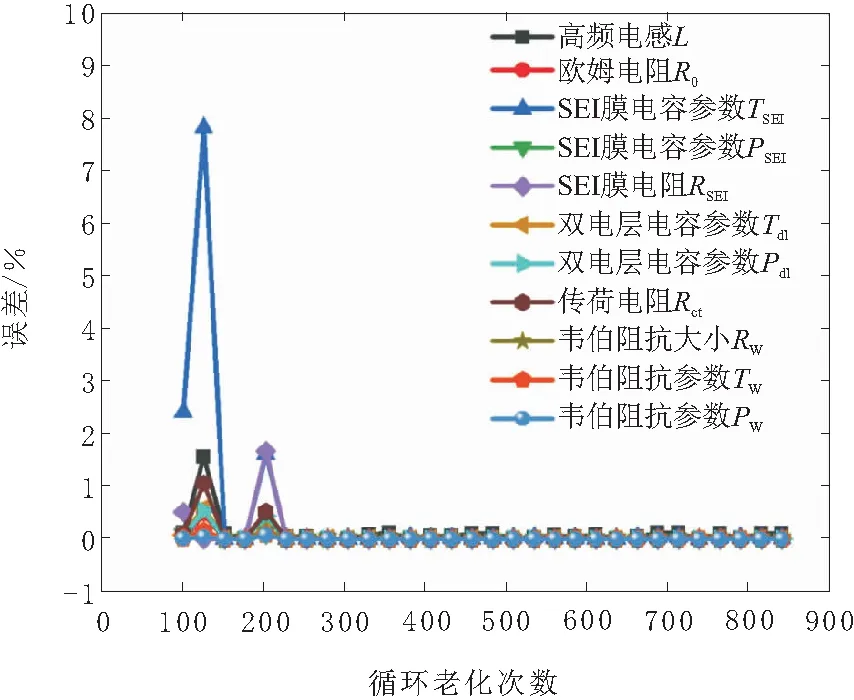
图5 25 ℃、70%SOC时不同循环次数下参数辨识误差

图6 循环老化125次与循环老化525次阻抗谱
同时对电池循环老化425次后各个温度与荷电状态的阻抗谱进行解析,各个电路元件参数辨识结果误差分布如表3所示。
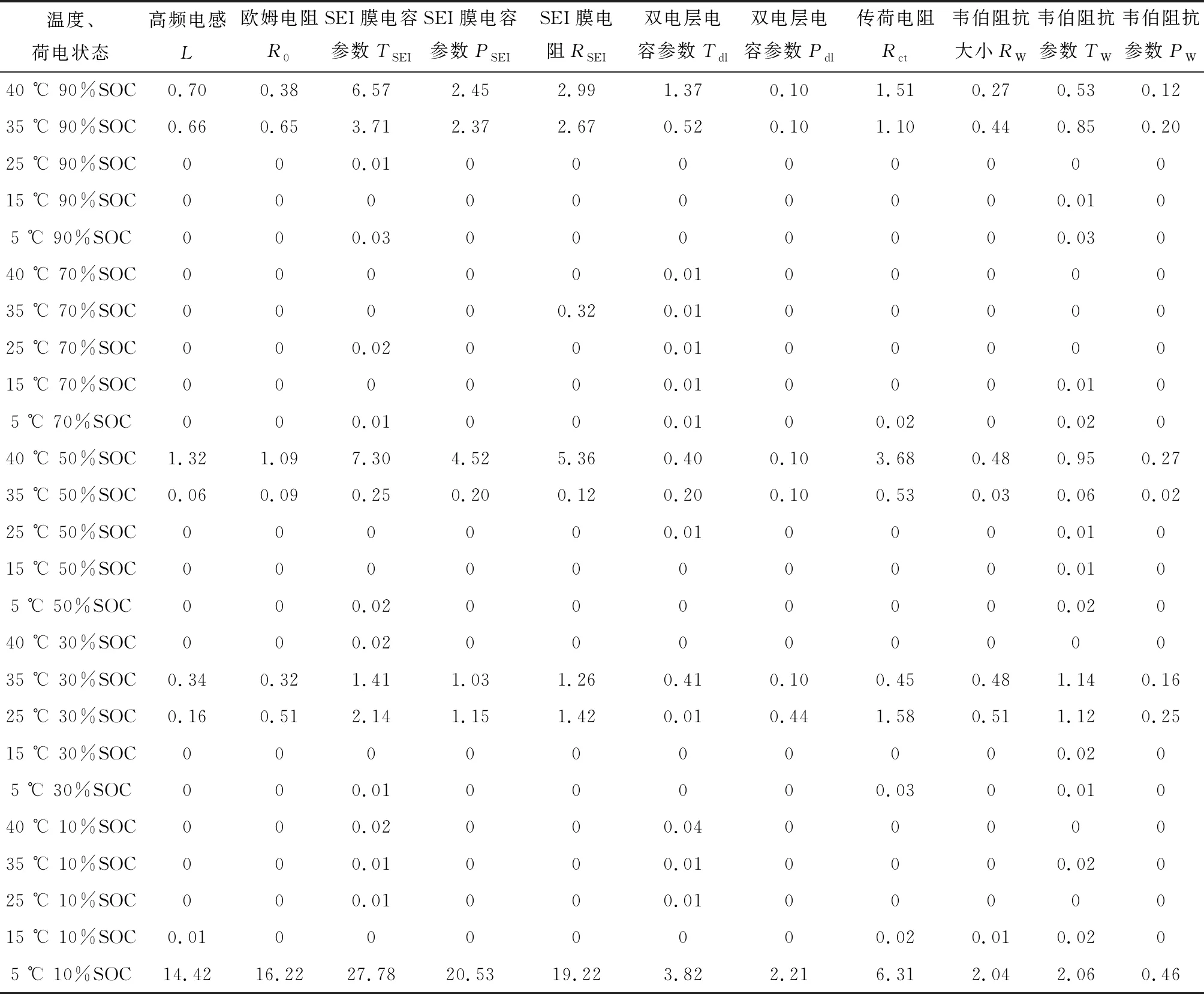
表3 循环425次后不同温度、荷电状态下参数辨识误差分布 %
由表3可知,除了5 ℃、10%SOC下的阻抗谱辨识结果误差较大,其余各个状态下电路元件参数辨识误差均小于8%,且绝大部分温度与荷电状态下元件累积误差接近于0。同时从表3中可以观察到,累积误差分布主要集中于高温(35 ℃、40 ℃)状态。循环425次、40 ℃、50%SOC和90%SOC下阻抗谱如图7所示。
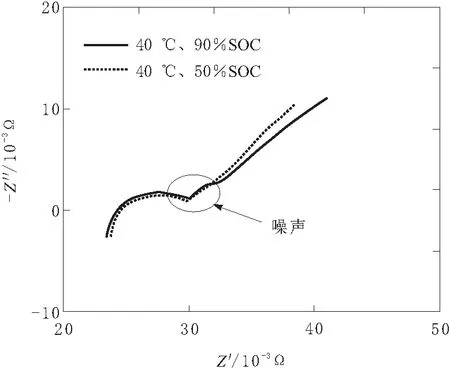
图7 循环425次、40 ℃,50%SOC和90%SOC下阻抗谱
由图7可知,误差仍来源于阻抗谱噪声的影响,特别在高温下阻抗变小使得噪声对阻抗拟合影响相对变大。
循环425次、5 ℃、10%SOC下阻抗谱如图8所示,分析图8辨识结果误差较大的原因,可以发现,虽然电池阻抗在低温与低荷电状态下显著增加,但系统测量噪声分布范围包含了高中频圆弧,使得阻抗谱发生了畸变,因此使得该方法与Z_view的辨识结果产生较大的差异。

图8 循环425次、5 ℃、10%SOC下阻抗谱
4 结束语
本文首先对用于拟合电池电化学阻抗谱的等效电路模型进行了解释说明并给出了其表达式。针对商用软件在等效电路模型参数辨识过程中需要多次手动调整、不利用车载阻抗应用的情况,提出了从分段局部拟合出发的无干预锂离子电池等效电路模型参数辨识方法。
通过实验对比发现,本文提出的方法对电池不同老化、温度、荷电状态下的阻抗谱等效电路模型参数辨识结果与商用软件Z_view的辨识结果相比误差较小,且在测量噪声影响较小的情况下参数辨识结果与Z_view保持一致,证明了该方法的有效性,从而为在线利用阻抗谱进行电池状态量化估计提供了重要工具。
另一方面,阻抗谱测量噪声的存在对本文方法的辨识结果有一定影响,如何在噪声影响特别大的情况下进一步提高算法的辨识精度将是下一阶段工作的重点。
