正交铺层碳纤维复合材料板电涡流分布三维有限元仿真
2021-04-27王黎明
姜 磊,王黎明
(1.核工业理化工程研究院,天津 300180; 2.粒子输运与富集国防重点实验室,天津 300180)
0 引言
碳纤维复合材料(CFRP)由于具备比强度高、比模量高、可设计性强等优良特性,在航空航天、车辆工程、建筑工程等领域广泛应用[1-2]。碳纤维复合材料由碳纤维束和树脂两部分组成,通过碳纤维束的铺层角度设计可以获得性能各异的复合材料结构。
电涡流检测方法已越来越多地被用于碳纤维复合材料的位移测量、厚度检测、缺陷检测等[2-4]方面,成为该种材料无损检测的重要技术。有效、准确地计算得到被测物体的电涡流分布规律是电涡流检测方法中需要解决的核心问题之一。相比传统金属材料,碳纤维复合材料具有弱导电性特点,且其磁电性能表现出显著的各向异性特点[5]。这些特点为其电涡流分布计算带来困难。
曾辉耀等[3]采用COMSOL Multiphysics 有限元软件,进行电涡流法检测单向CFRP分层缺陷问题研究。徐帅等[4]提出一种基于矢量磁位-标量电位的电磁有限元分析方法,计算了CFRP纤维方向、材料缺陷对探头电参数的影响。Hongu等[6]采用实验方法对有缺陷CFRP涡流强度分布进行了测量。近年来,ANSYS有限元软件也被应用于金属材料电涡流检测的数值仿真。张玉宝等[7]采用ANSYS仿真分析了探头参数对电涡流检测性能的影响。廖珍贞等[8]采用ANSYS对间隙传感器的检测线圈间距进行了仿真优化。王志春等[9]采用ANSYS建立了电涡流测多层45#钢薄板厚度仿真模型,并对线圈尺寸进行了优化。Wilde 等[10]、张兴兰等[11]也利用ANSYS有限元法,对电涡流法检测金属试件进行了仿真计算以及传感器优化设计分析。
基于上述背景,本研究将ANSYS有限元软件应用于正交铺层CFRP电涡流检测仿真,借助APDL语言编写命令流,建立了三维有限元仿真模型,对CFRP平板电涡流分布规律进行了计算。研究结果对于CFRP材料电涡流检测技术开发具有指导意义。
1 三维有限元仿真模型建立
1.1 几何模型建立
本研究建立的正交铺层CFRP板和测试探头几何模型如图1所示。在电磁学仿真分析中,需要把空气介质考虑在内,建立了圆柱形几何空间来模拟空气区域。仿真中采用的几何模型基本参数如表1所示。
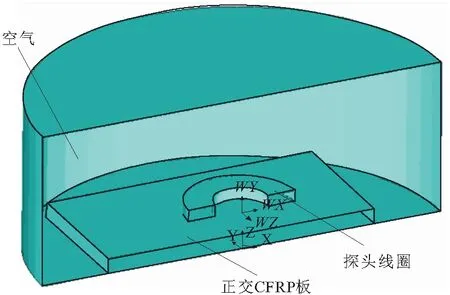
图1 几何模型(剖视图)

表1 模型基本参数
1.2 材料参数设置
探头材料为各向同性材料,相对磁导率设置为1.0,电导率设置为6.0×107S/m;空气同样为各向同性材料,相对磁导率设置为1.0,电导率设置为1.0×10-8S/m。
正交铺层CFRP为典型的各向异性材料,其磁导率各方向上相对磁导率均设置为1.0,但电导率的设置需要考虑各向异性。建立如图2所示的坐标系,x-y平面与CFRP板上表面平行,x向、y向以及x-y平面的法向为CFRP材料的3个主方向。

图2 CFRP电学参数计算坐标系
电导率张量为
(1)
σl为x向电导率;σt为y向电导率;σcp为x-y平面法向电导率。
将x-y坐标系绕原点逆时针旋转角度θ,得到新坐标系x′-y′,电导率张量在新坐标系为
(2)
根据正交铺层CFRP材料的电磁特性,分别将3个主方向上的电导率σl、σt、σcp设置为6.0×103S/m、6.0×103S/m和10.0 S/m。
1.3 单元设置
采用ANSYS软件中的8节点六面体单元Solid97模拟空气、探头、正交铺层CFRP板,对三者分别设置不同的单元属性。同时,对探头所有单元的电流自由度进行耦合,对正交铺层CFRP板的电压自由度进行耦合。
1.4 边界条件和求解设置
在空气区域外围设置第1类边界条件,即狄利克莱边界条件,令磁通量平行于外边界。设置ANSYS求解类型为谐响应分析,通过HARFRQ命令设置激励频率f为1.0×106Hz,将探头线圈的激励电压值U设置为12 V。
2 正交铺层CFRP板电涡流分布仿真结果
通过ANSYS仿真计算,得到整个模型的电涡流三维分布云图,如图3所示。从计算结果可以看出,ANSYS可以有效计算获得正交铺层CFRP板电涡流分布规律。对于整个模型而言,电涡流主要分布在探头线圈和正交铺层CFRP板内,空气区域中电涡流强度为0,符合实际物理意义。正交铺层CFRP板中涡流三维分布规律表现为:涡流强度呈现沿径向先增大后减小、沿深度方向不断衰减的分布特点。为进一步研究CFRP板电涡流分布特点,提取CFRP板上表面电流密度分布云图,如图4所示。由图4可知,CFRP板电涡流呈现轴对称分布规律,对称轴线与探头线圈轴线重合。

图3 有限元模型的电涡流三维分布云图

图4 CFRP板上表面电涡流分布云图
为了进一步研究电涡流分布的影响因素,下面分别针对线圈激励频率f、激励电压值U以及线圈与CFRP板之间距离d共计3个参数进行单因素分析。具体给出各因素对涡电流强度、电流密度沿径向及深度方向分布情况的影响规律。
3 正交铺层CFRP板电涡流分布影响因素分析
3.1 线圈激励频率影响规律
设定不同的激励频率,其他计算参数沿用上文介绍参数值。通过仿真结果数据分析,得到不同激励频率下,正交铺层CFRP板电涡流强度分布规律,分别如图5和图6所示。

图5 不同激励频率下正交铺层CFRP板电流密度径向分布

图6 不同激励频率下正交CFRP板电涡流沿深度方向分布
图5和图6计算结果表明:随着激励频率变化,CFRP板电涡流分布形态保持不变,最大电流密度对应的径向位置保持恒定;涡流强度随频率增加呈现先增加后减小特点,当激励频率为3×105Hz时,电涡流强度达到最大值。
3.2 探头激励电压值影响规律
设定不同激励电压值,激励频率设定为1 MHz,其他计算参数沿用上文介绍参数值。通过仿真结果分析,得到不同激励电压下,正交铺层CFRP板电涡流分布规律,分别如图7和图8所示。
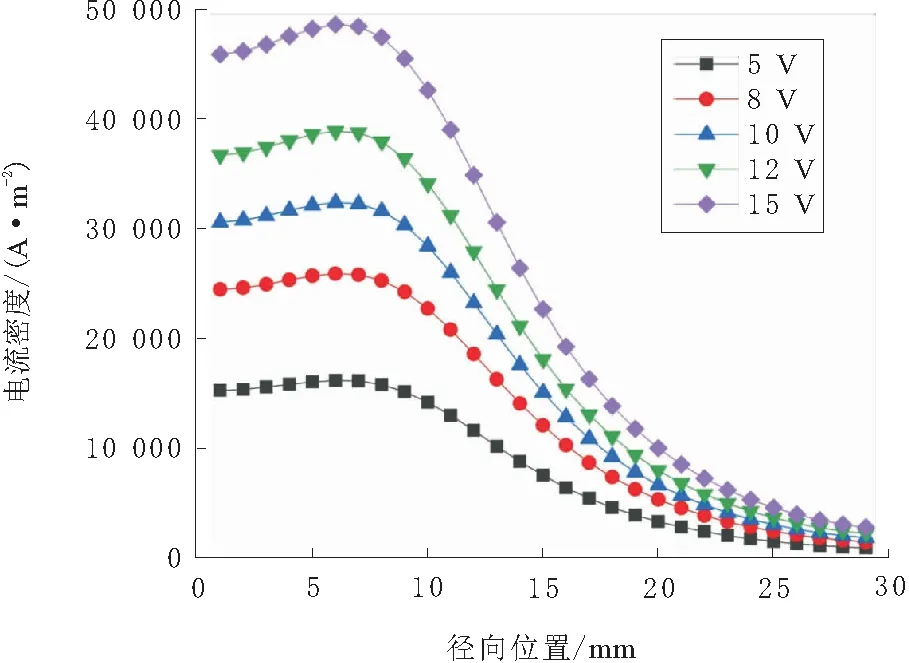
图7 不同激励电压下正交铺层CFRP板电流密度径向分布
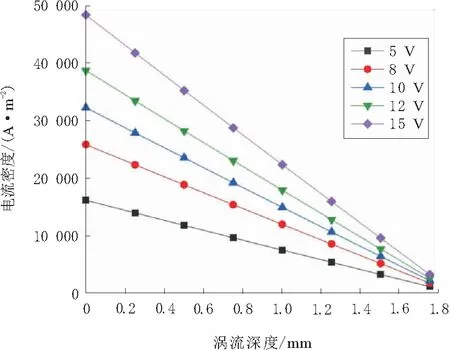
图8 不同激励电压下正交CFRP板电涡流沿深度方向分布
图7和图8结果表明:随着激励电压幅值变化,CFRP板电涡流分布形态保持不变,最大电流密度径向位置也保持恒定;随着激励电压值增大,涡流强度不断增加,涡流强度与激励电压值呈正比关系。
3.3 探头线圈与CFRP板距离影响规律
通过调整探头线圈在计算坐标系中z方向的位置,不断改变线圈与CFRP板距离,激励电压幅值设置为12 V,激励频率设置为1.0×106Hz,其他计算参数沿用上文介绍参数值。通过仿真得到不同距离条件下,正交铺层CFRP板电涡流强度分布规律,分别如图9和图10所示。
图9和图10计算结果表明:随着线圈与CFRP板之间距离变化,CFRP板电涡流分布形态显著变化;随着距离的增加,最大电流密度出现的径向位置不断向中心移动,电流密度沿径向分布亦不断趋向平坦,电流密度沿深度方向衰减斜率不断增大。
最大电流密度径向位置随距离变化曲线如图11所示。由图11可知:当探头线圈与CFRP板之间的距离增大到2.5 mm之后,最大电流密度的径向位置随着距离增加继续向中心轴线靠拢;距离每增加0.5 mm,最大电流密度与中心轴线距离减小1.0 mm。
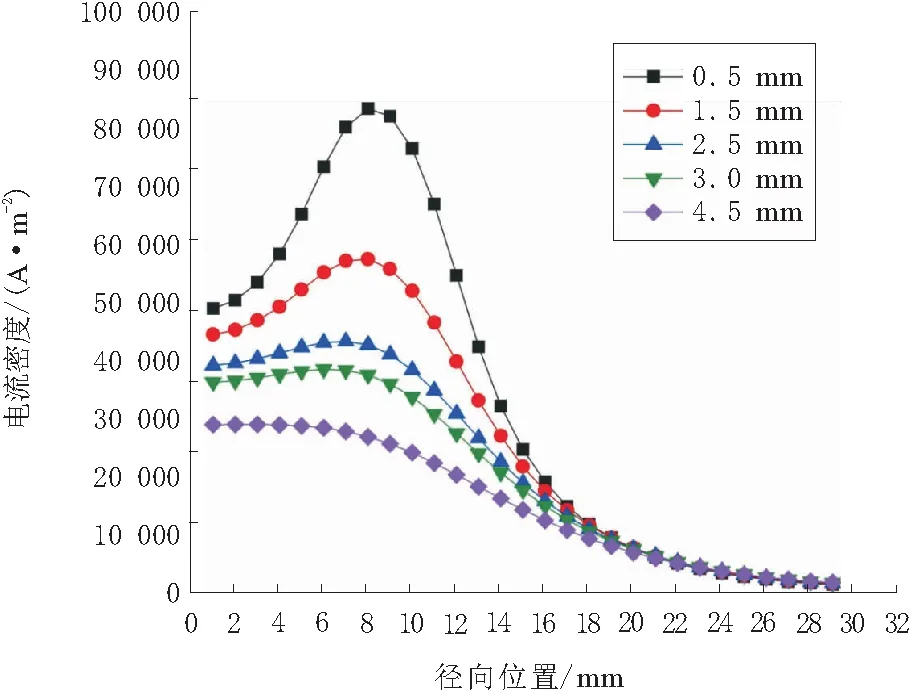
图9 不同距离下正交铺层CFRP板电流密度径向分布
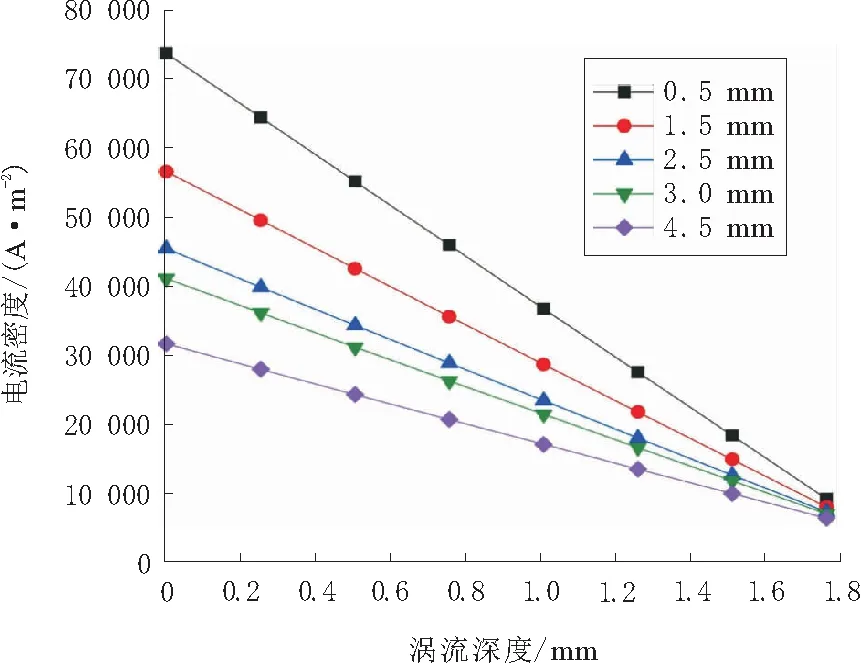
图10 不同距离下正交CFRP板电涡流沿深度方向分布
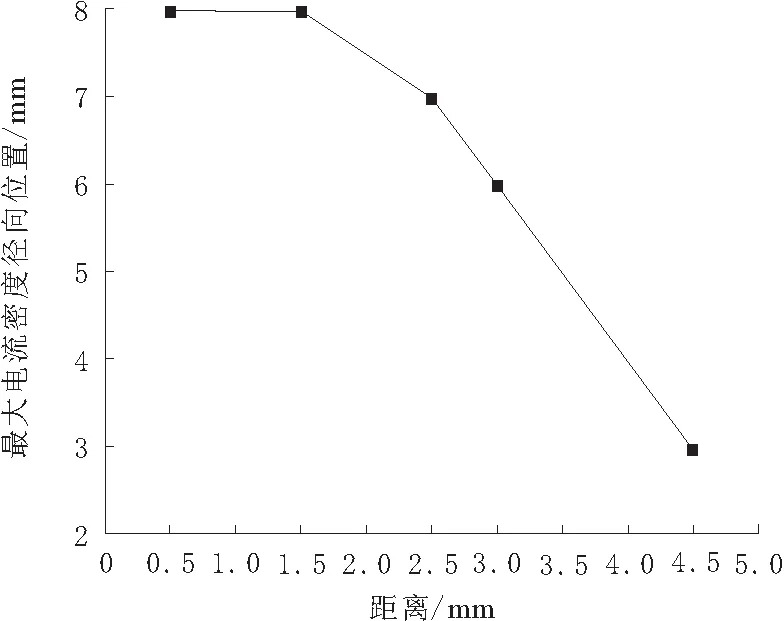
图11 最大电流密度径向位置随距离变化曲线
4 结束语
采用ANSYS有限元法实现正交铺层CFRP板电涡流分布规律的三维仿真分析,CFRP板电涡流呈轴对称分布,电涡流强度沿半径方向先增加后减小,沿深度方向呈现近似线性衰减规律。
单因素影响分析表明,探头线圈激励频率、激励电压、探头线圈与被测试件之间距离均是影响正交铺层CFRP板电涡流分布规律的主要因素。
其中,激励电压和激励频率只影响电涡流强度,不影响电涡流分布形态,而探头线圈与被测件之间距离则对电涡流分布形态和涡流强度均有显著影响。
