基于材料特征的超声数值模拟仿真模型实验研究
2021-04-27王翔宇
李 冬,王翔宇
(1.吉林医药学院生物医学工程学院,吉林吉林 132013;2.吉林大学材料科学与工程学院,长春 130012)
0 引言
随着科学技术的不断发展,超声学被应用于众多领域,其中最为重要的一个应用是脉冲超声在工业无损检测和评价中的应用[1-3]。在工业无损检测及评价过程中,超声系统在不破坏材料内在结构的前提下,可以通过超声特性来获取材料体的内在信息[4]。在超声波系统中,传感器由一系列材料层组成。而上述多层材料传感器因涉及物理声学,电子模拟和材料声学性能等多方面理论,其设计优化是一项极为复杂的工作[5-10]。在实际工作中,由于缺乏这些材料的频率和温度依赖性特征等信息使得该项工作开展起来更为困难[11-12]。虽然可以通过反复的试验找到材料的最佳组合,但该种方法势必会消耗相当多的时间和试验费用,通过使用数值模拟技术则可以弥补上述两方面的不足。多年来,许多专家研究一维声学现象,并对其进行电学类比。梅森等人用集总等效电路对机电换能器建模。雷德伍德在梅森的模型中编入了一条传输线路,以获取压电式换能器瞬时反应的有用信息。莫里斯通过使用SPICE(以集成电路为重点的模拟程序),用集成电路作为负极电容器的近似物,模拟了梅森模型的实际操作。克里姆霍尔兹等人给出了用于初级压电式换能器的另一等效电路。希尔赛康等人运用局部相互作用法(LISA)对声波在局部谐振器组成的声子晶体中的传播进行了数值模拟。而本文将普特摩尔等人的方法运用于液体和电压换能器上,进行在此类材料中一维声波传播的电学模拟。
1 模型的建立
通过可控电流和电压源对压电现象建模如图1所示。等效电路由静态电容C0(电极间电容)、一条传输线路(代表压电换能器的机械部分)以及两个用于耦合电路的电学和机械部件的控制源组成。假设一个超声波脉冲以有限的速度c(m/s)穿过媒介。可以将此脉冲描绘成一种干扰,媒介对其作出反应。在纵波的情况下,这种干扰为压缩或是物质的稀疏。媒介对这种干扰进行转移,从而恢复到自己的平衡态。媒介内的压缩或稀疏和媒介密度ρ(kg/m3)有关,而回复力与媒介的体积模量M(Pa)有关[13-14]。
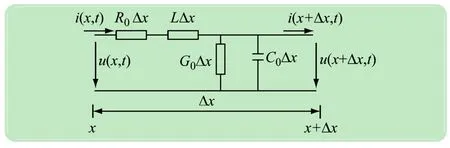
图1 长为Δx的传输线路段等效电路
同样,电脉冲可以在输电线路中传输。在一段短暂而有限的时间之后,线路的另一端接收这些脉冲。脉冲以特定的速率传输。与声波相似,电脉冲是电子在传输线路中的浓聚和稀疏程度[15]。用电路参数贯穿分布于线路之中的分布参数网络作受损传输线路的近似物,一段长为Δx的线路段可近似为图(1)中的电路。
有耗传输线路模型由4个参数加以描述,R0为单位长度两个导体中的电阻,Ω/m;L0为单位长度两个导体中的电感,H/m;G0为单位长度电介质的电导,S/m;C0为单位长度导体间的电容,F/m。在无损条件下,R0和G0为0。为推导出这些参数,在图1所示电路中运用基尔霍夫电压定律:


由上式可得出一个含有R0和L0的公式,通过进一步推导可得到另一个关于G0和C0的公式,应用基尔霍夫电流定律可得:

式(3)、(5)都是一阶偏微分方程,同时也被叫作传输线路一般方程。若电压u(x,t)和电流i(x,t)是时谐余弦函数,这些方程可以简化为:

式中,ω 为角频率。通过式(6)、(7),式(3)、(4)的传输线路一般方程就可改写为:

这些方程均为传输线路时序方程。通过使用这些方程[式(8)、(9)]可以推导传播常数和线路的特性阻抗。通过式(8)、(9)对x进行微分后可得出:
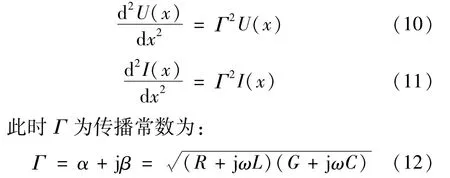
式中:α为衰减常数,Np/m;β为线路的相位常数,rad/m。式(10)的一般解为:
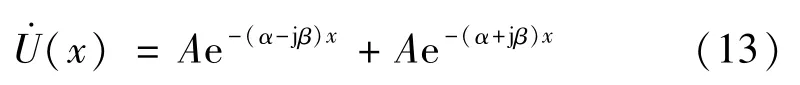
若要在式(13)中加入时间相关性,可以将式(13)乘以ejωt,由此可进一步得出:

式(14)中包含两个行波。一个以振幅A沿着正方向x行进,振幅的衰减率为α;另一个以振幅B沿着相反方向行进,振幅的衰减率相同。同一类型的微分方程控制着声波的传播。在声波为谐波的情况下,对应式为式(10)、(11),可得出有损线性平面声波方程:

式中:p(x,t)为压力,Pa;u(x,t)为质点速率,m/s。与Γ 相同,kc为由衰减常数α,(Np/m)和波数k(rad/m)组成的复波数。波动方程(15)的一般解为
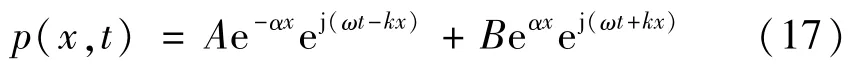
式(17)和式(14)所表示的传输线路的解法相同。式(16)的解法也为同一形式。复波数kc为
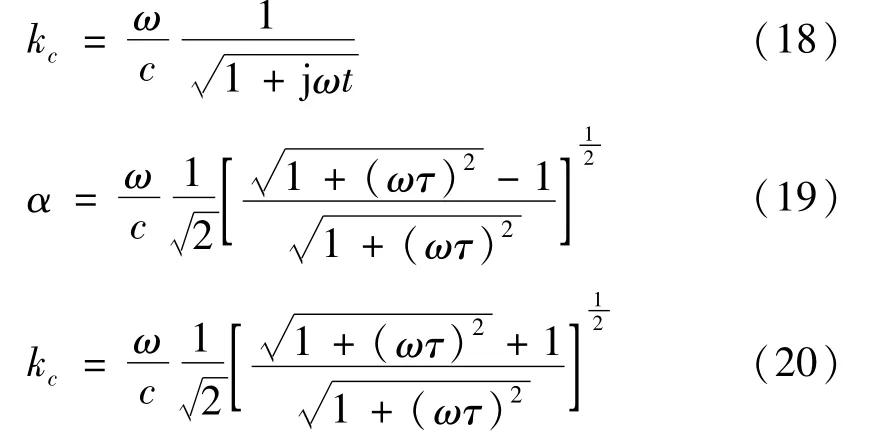
式中:τ为控制系数;c为比例系数。为了综合两种理论,这里选用阻抗型类比,用电压代表机械力,用电流代表质点速率。特性阻抗在边界处重要起来,此时需要满足连续性条件。在边界处时,压力和法向质点速率必须是连续性的,因为电压和电流必须在连接点保持连续性。在有损传输线路中,特性阻抗

而对于有损声媒介来说,特性阻抗Za为:

式中:τ为控制系数;c为比例系数;ρ为媒介的密度。
扩展式(21)、(12)后得出:
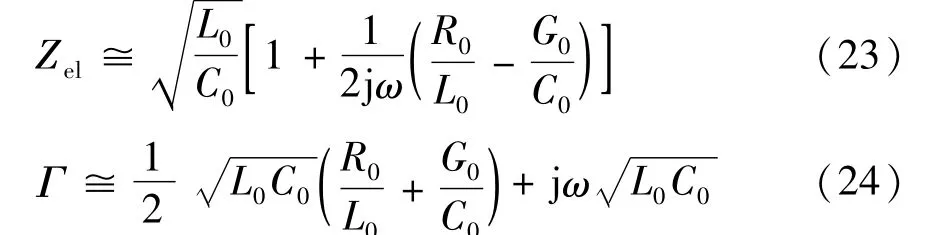
考虑到R0≤ωL0,G0≤ωC0时,微小却不可忽略的损耗,因此式(23)中的第2项可以忽略不计,使特性阻抗为与式(22)类似,低损耗声特性阻抗可以约等于pc。而且,式(20)中的波数变为ω/c。为了使两种特性阻抗相互关联,选用了阻抗性类比。
其中电压代表力(不是压力),电流代表质点速率。两个体系之间的等量关系为:

而A(单位m2)是声波传播的横截面积。再加上低损耗特性阻抗公式的定义,便可得出以下关系式:

式(24)的实数部分是衰减常数,因而

与声衰减的传统理论做一对照,αcl=αv+αtc,其中αv是黏滞损失产生的衰减的系数,αtc是热传导损失产生的衰减的系数。根据式(26)~(28),可以解出R0和G0,为这些衰减现象建模,

本文中使用的材料层热导率低,热传导产生的损耗可忽略。因而可认为电导G0=0。因此,式(26)、(27)和(29)是模拟所需的最终公式。
2 试验装置
脉冲发生器-接收器的原理框图如图2所示。其中RF(无线电频率)脉冲发生器产生无线电频率尖脉冲,频率范围1~10 MHz,脉宽2~60 μs。脉冲重复率为1 kHz。RF脉冲被输给超声波换能器(压电式)中。换能器激发并发送脉冲,使其穿过样品。位于样品另一端的接收换能器将接收到的超声波脉冲转化为电信号(RF脉冲)。脉冲发生器的具体细节由亚威尔等人提出。RF脉冲被输给到一个放大器中。该放大器由晶体管BF195等元件组成。单级放大器的输出至IC CA3028集成放大器。放大器的综合特性为:增益为50 dB;带宽=15 MHz;输入阻抗=15 kΩ。由于负反馈深,IC 3028放大器的稳定性高出许多。检测信号经过LM 393(宽频带零交叉探测器)后,检测到的信号被输给到单位增益缓冲器处。缓冲器的设计中使用了高速度、低功率的运算放大器AD 826。AD826的特征是50 MHz单位增益带宽、30 V/μS转换速度、70 ns稳定时间,最大输入补偿电压为0.01%,2.0 mV。随后将这条检测到的信号发出,复位输入RS触发器。通过RF脉冲发生器的IC 74121的输出来设定触发器。
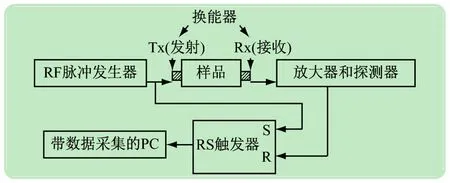
图2 实验配置示意图
脉冲穿过样品所花费的时间。用分辨率为10 ns的计时器测量。至于速率和衰减的测量,发送换能器牢牢固定在测量元件(图4)的一端,而接收换能器固定在分辨率至少为10 μm的可移动刻度以上。该系统通过12 bit的DAS(数据采集系统)卡和PC(个人电脑)交流。为了进行交流,对超声波系统GUI(图形用户界面)加以控制,并设定其参数(图5)。GUI提供了通用数据表示功能。在GUI中,几乎可以改变所有测量信号的参数和信号处理过程中的参数。为了和系统连接,使用了Dynalog系统控制驱动的函数。然后设定参数,与系统进行交流。在窗口(图5)中,可以选择信道号、极性(单极/双极)和使用了DAQ配置框的范围。“运行DAQ”框中,通过命令键“打开”来打开卡片,通过命令键“关闭”来关闭卡片。命令键“开始扫描”对数据进行抽样(电压等级和时间),并在缓存记忆中储存。命令键“停止扫描”停止抽样过程。测量和分析接收到的超声波信号在“测量和分析”框中进行。命令键“瞬态响应”框会打开一个新的窗口,显示抽样数据的瞬态响应。通过使用光标点,可以测量接收信号的时间和脉冲高度。数据储存于数据库,以用于进一步分析。
3 模拟配置
类似的电路配置如图3所示。图3中展示的脉冲发生器电路系统由一个使用脉冲源(u2)的脉冲发生器构成。脉冲电压为5 V,延迟时间为0 s,上升和下降时间为1 ns,脉宽为2 μs,周期为1 ms。而另一正弦源(u3)无补偿电压,峰值电压为5 V,延迟时间为0 s,频率为5 MHz,阻尼系数和相位延迟为0。其后便是TTL7400、7407、1 kΩ 电阻器(R3)、20 V 直流供电、2 nF电容器(C3)。脉冲始于20 V,在2 μs之内减至0 V。电容器输出和换能器的电学部分以及并联的阻尼电阻(R4)相连。
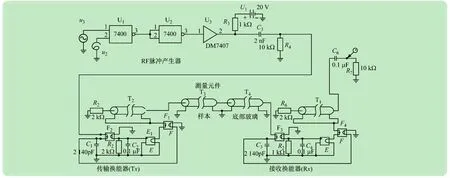
图3 实验配置的模拟电路
4 信号处理

图4 5 MHz的换能器在25℃的四氯化碳中接收的前36 μs脉冲对比图
把实验中接收的信号和时域中的模拟信号加以比较,模拟信号见(a),测量信号见(b)。图4为5 MHz的换能器在25℃的乙醇样本中接收的前30 μs脉冲。图5所示为5 MHz的换能器在25℃的甲醇中接收的前32 μs脉冲。图6所示为5 MHz的换能器在25℃的四氯化碳中接收的前36 μs脉冲。表1给出了对二元液体混合样本超声波速率以及衰减的测量数值和模拟数值的对比。
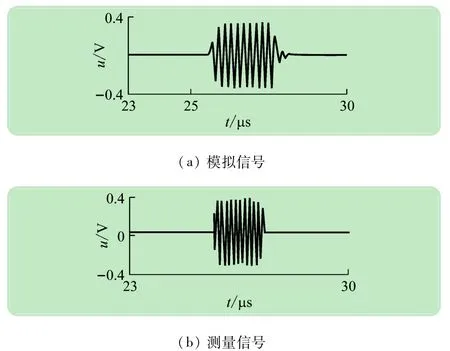
图5 5 MHz的换能器在25℃的丙酮中接收的前30 μs脉冲对比图
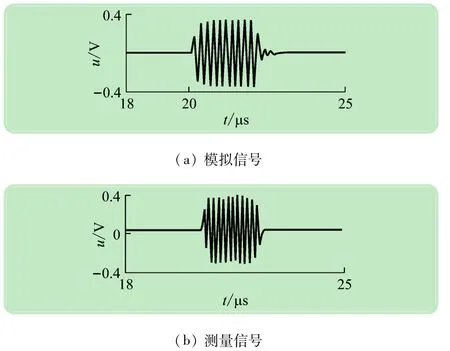
图6 5 MHz的换能器在25℃的蒸馏水样本中接收的前25 μs脉冲对比图

表1 液体样本超声波速率以及衰减的文献数值和模拟数值对比表
5 结语
本文对声媒介和传输线路之间的类比进行了回顾,并讨论了使用控制源的超声波换能器的类比电学模型。文中呈现了一个完整超声波体系的模拟模型,并将模拟中接收到的信号和时域中的实际测量数据进行对比。模拟和实验数据的对比表明,声波传播相关且受到温度、频率影响的参数是可以建模的。这种可行性已经在用于物理特性调查的超声换能器配置中得到证明。对声音在乙醇、甲醇、四氯化碳、丙酮、苯和蒸馏水中的衰减量和速率进行了对比。关于这些材料得出的结论是积极的。因此,模拟软件为在构型前预测将要接收的信号创造了途径。此外,使用超声波模拟程序包也为附属电子增强和处理收到的信号提供了发展空间。
·名人名言·
人类需要善于实践的人,这种人能由他们的工作取得最大利益;但是人类也需要梦想者,这种人醉心于一种事业的大公无私的发展,因而不能注意自身的物质利益。
——居里夫人
