柔性机械臂轨迹跟踪的迭代学习控制

蔡 军，罗 成，谢 薇，方志远

（重庆邮电大学自动化学院，重庆 400065）

0 引言

随着科学技术的迅猛发展，机械臂的控制技术已经涉及机械，电气，自动化等众多的科研领域［1］。但是，在一些特殊的工况条件下，传统的刚性机械臂由于能耗高、运行速度慢、操作空间有限等原因，已经无法满足要求。因此，具有轻质、重载、高灵活性特点的柔性机械臂成为当今机器人研究的热点。柔性机械臂的动力学系统非常复杂，具有非线性、强耦合的特点，并且在操作柔性机械臂的过程中，由于臂杆自身的材料属性，会有刚柔耦合现象产生［2］。这给柔性机械臂的控制带来了挑战。文献［3］中采用了自适应PID控制器，自动在线调整控制增益，解决了单连杆柔性机械臂在执行器失效后的情况下的控制问题。文献［4-5］中研究了自适应径向基函数神经网络滑模控制器，利用神经网络来自适应逼近补偿系统建模过程中的不确定项，然后，在此基础上设计了滑模控制器来实现轨迹跟踪。文献［6］中针对柔性机械臂参数不确定性问题，提出了利用卡尔曼滤波在线估计的方法来逼近模型的动态。

迭代学习控制适用于具有重复运动性质的对象，仅通过足够多次的重复迭代，就可以使执行对象达到期望的要求［7-9］。因此，对于具有重复运动性质的柔性机械臂系统很适用。迭代学习控制的初始状态问题一直是迭代学习控制理论的一个研究热点。早在1991年，Lee等［10］提出：如果每次迭代时，系统的初始状态不相等或者系统的初始状态存在很小的偏差都会导致系统发散。原因是信号的偏差会随着迭代次数的增加而累加。迭代学习的初始状态问题可以分为3类：第1类是系统设定初值等于期望初值；第2类是系统设定初值等于任一固定值（但不等于期望值）；第3类是系统设定初值等于任意值［11-13］。孙明轩等［14-15］提出在进行系统控制输入迭代学习的同时，初态也进行迭代学习的控制算法。这样就放宽了初始定位的条件，提高了控制系统的鲁棒性。吕庆等［16-17］针对一类非线性系统，在时间轴上设计了一个随迭代次数增加而缩短的修正区间，在该时间段内对初始偏差进行修正，该时间段外实现系统输出跟踪期望输出。

本文基于文献［18］中的二连杆柔性机械臂系统模型，提出了初态偏差加速修正的PD型迭代学习控制算法，解决了该系统迭代学习控制方案中因柔性材质属性使得系统每次迭代初始状态不同，造成的被控系统控制精度不够高的问题。

1 柔性机械臂的动力学模型

二连杆柔性机械臂系统各变量定义如图1所示：τ1和τ2分别为两个伺服电动机逆时针方向产生的力矩；m1和m2分别为连杆1、2的质量；l1和l2分别为连杆1、2的长度；θ1和θ2分别为两个伺服电动机产生的伺服角；q1和q2分别为连杆1、2运动过程中产生的偏转角，表征柔性杆的振动情况；XOOYO为地面参考坐标系，X1OY1和X2O′Y2分别为连杆1、2的局部坐标系。文中柔性连杆1、2的长度均远大于横截面的宽度，因此将该柔性机械臂视为欧拉-伯努利梁，只考虑柔性连杆弯曲引起的变形。并且该系统只在水平面旋转运动，因此忽略重力因素的影响。

二连杆柔性机械臂系统的动力学方程为［18］

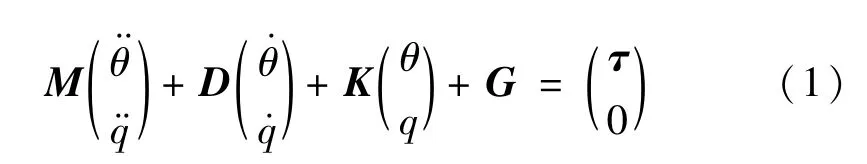
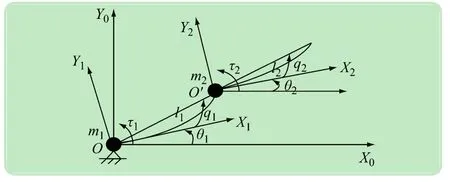
图1 二连杆柔性机械臂

式中：θ＝［θ1；θ2］分别为两个伺服电动机产生的伺服角；q＝［q1；q2］分别为连杆1、2 运动过程中产生的偏转角；τ ＝ ［τ1，τ2］为系统的输入矩阵；M∈R4×4为惯性矩阵；D∈R4×4为离心力和哥氏力矩阵；K∈R4×4为刚度矩阵；G∈R4×1为重力矩阵。

对矩阵进行分块处理有：

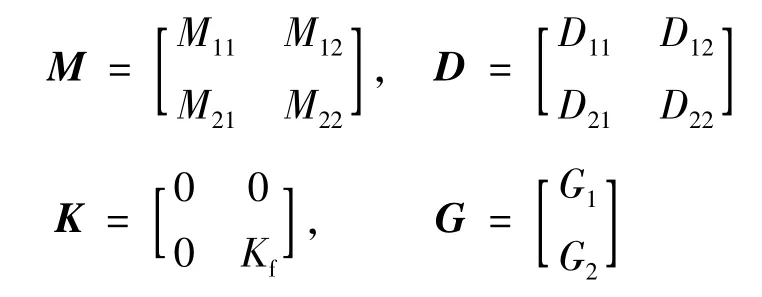
式中：Mij∈R2×2；Dij∈R2×2；Kf∈R2×2；Gij∈R2×1，i，j＝1，2，均为对应的块矩阵。

考虑到二连杆柔性机械臂的动力学方程（1）中包括伺服角θ和偏转角q两部分变量。在柔性机械臂系统轨迹跟踪控制中偏转角q无法直接测得，方程（1）可写为以下两式：

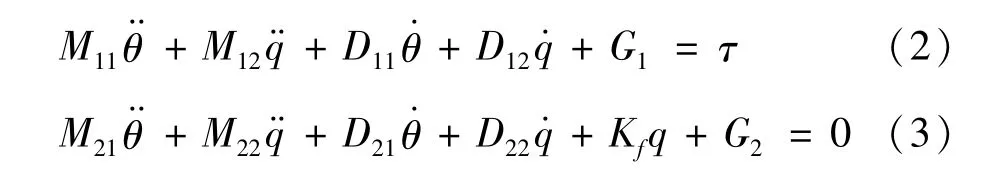
由式（3）可见，机械臂内部的偏转角q是受伺服角θ影响而产生的变化。由式（3）可进一步得到：

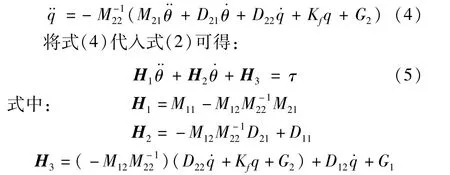
虽然方程（5）在形式上与刚性机械臂的动力学方程相似，H1类似于刚性机械臂的惯性矩阵，H2类似于刚性机械臂的离心力和哥氏力组成的矩阵，H3类似于刚性机械臂的重力矩阵。但是，通过观察H1，H2，H3矩阵可以发现两者的区别在于：柔性机械臂系统的H1，H2，H3矩阵较刚性机械臂系统的惯性矩阵、离心力和哥氏力组成的矩阵、重力矩阵而言，除了含有伺服角变量θ还有偏转角变量q。

为了便于实现系统的轨迹跟踪这一目标，将方程（5）化为标准的非线性仿射系统。由于机械臂内部的偏转角q是受伺服角θ影响而产生的变化，因此令系统的状态量X（t）＝［θ］T，得到系统的状态方程：

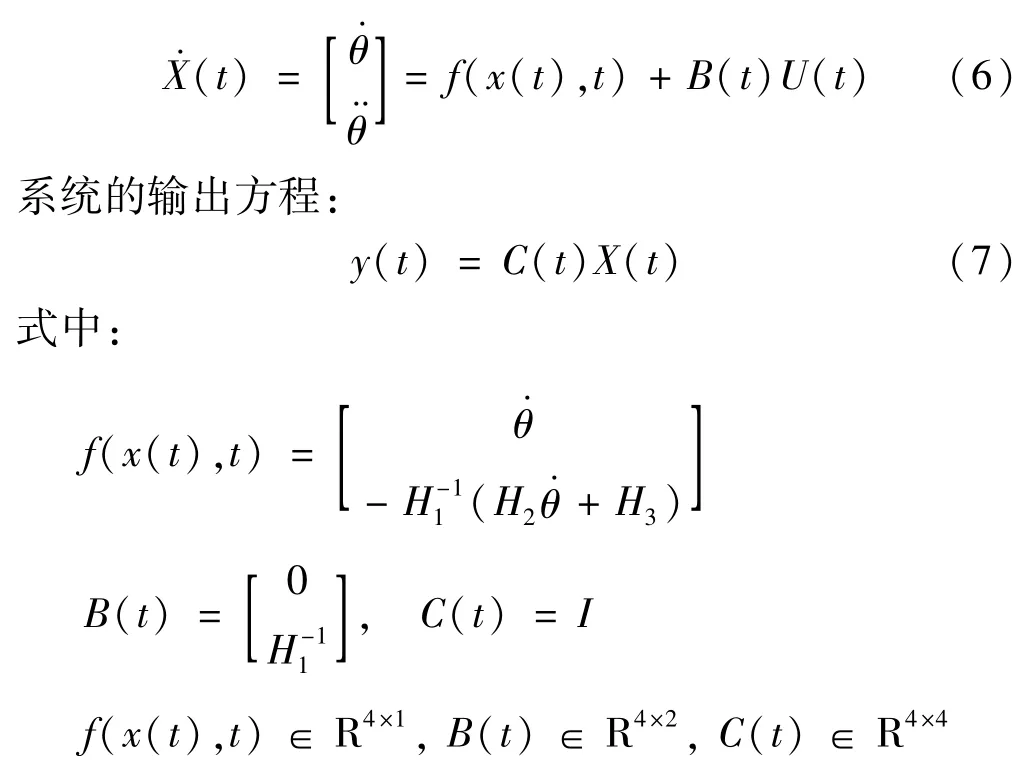
2 控制器设计

针对在有限时间间隔［0，T］内重复运行的二连杆柔性机械臂系统，设计了迭代学习控制器。假设该系统每一次迭代学习过程中，初始状态都不相同，第k次的迭代初态可表示为xk（0）。

定义系统的跟踪误差为：

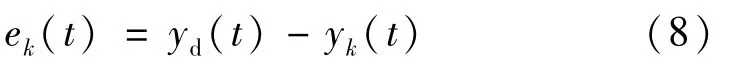
式中：yd（t）表示系统期望轨迹；yk（t）表示第k 次迭代时系统的输出。

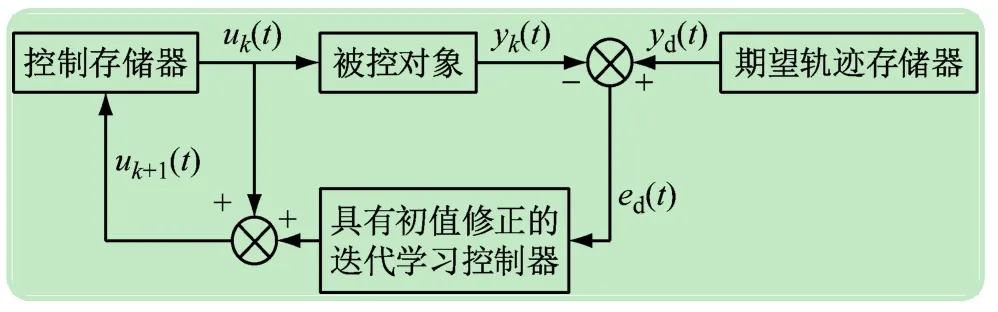
图2 初态加速修正控制器结构框图

图2是初态加速修正的PD型迭代学习控制器结构框图。当前次的控制量是由上一次迭代时的控制量、跟踪误差值、跟踪误差值的变化率及实时初值偏差，利用该算法的定义（在时间轴上设计了一个随迭代次数而缩减的修正区间，该区间内对初始状态偏差进行修正，修正区间外实现跟踪期望输出）并通过简单的代数组合构成的。其形式如下：

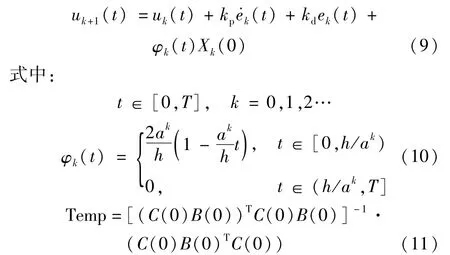
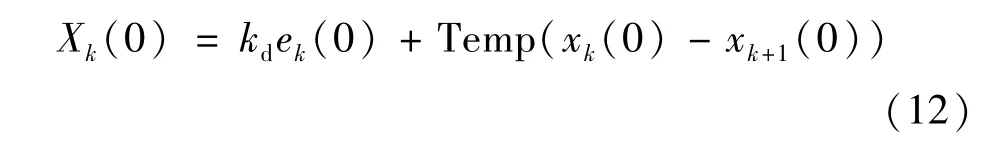
式中：a＞1，0＜h＜T，kp为比例学习增益；kd为微分学习增益，下标k为迭代的次数。

通过将学习算法式（9）用于系统式（6）、（7）施行迭代学习控制，则系统第k次迭代对应的状态方程为

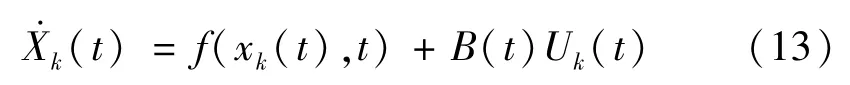
系统第k次迭代对应的输出方程为

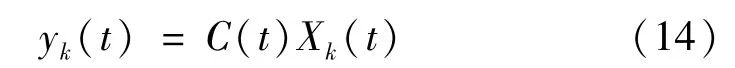
上述算法计算步骤如下：①利用方程（8）计算ek（t）；②利用方程（10）计算φk（t）；③利用方程（12）计算Xk（0）；④利用方程（9）计算uk＋1（t）；⑤将控制输入uk＋1（t）带入到系统控制器，并进行下一次迭代，重复①～④。

所提的迭代学习算法意义如下：

（1）当时间t∈［0，h／ak）时，由于存在初始状态值偏差，系统的输出不能跟踪上期望轨迹。

可以发现：当a＞1，迭代次数k趋于无穷大时，t∈［0，h／ak）→［0，0），初态偏差修正的时间区间正在缩短。

（2）当时间t∈（h／ak，T］时，被控系统的跟踪误差会被限制到一个可控的范围内。

3 仿真验证

为了验证本文所提算法的有效性，被控对象选用文献［18］中的二连杆柔性机械臂系统模型。系统各参数［18］如下：m1＝1.0 kg，J21＝9.4 ×10－3kg·m2，m2＝0.9 kg，J12＝ 0.230 4 kg·m2，l1＝ 0.349 3 m，J22＝0.010 7 kg ·m2，l2＝ 0.297 5 m，E1I1＝ 9.0 N·m·rad－1，J11＝ 0.011 1 kg ·m2，E2I2＝ 4.0 N·m·rad－1。

系统所要跟踪的期望轨迹为

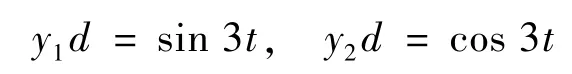
迭代学习控制器的参数为：

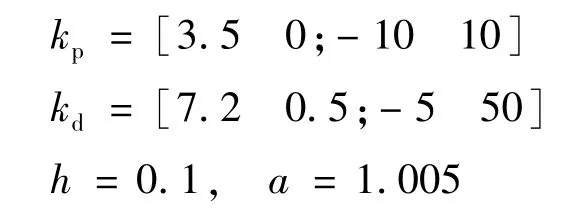
期望轨迹的初态为

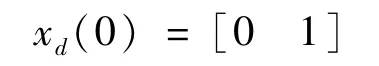
每次迭代的初态由rand函数自动随机生成。

图3给出了控制器在20次迭代学习下关节角1、2的轨迹跟踪过程图。可以看出：随着迭代的次数增加，时间轴上的修正区间在逐渐缩短。图4给出了控制器在第20次迭代学习下关节角1、2的轨迹跟踪图。

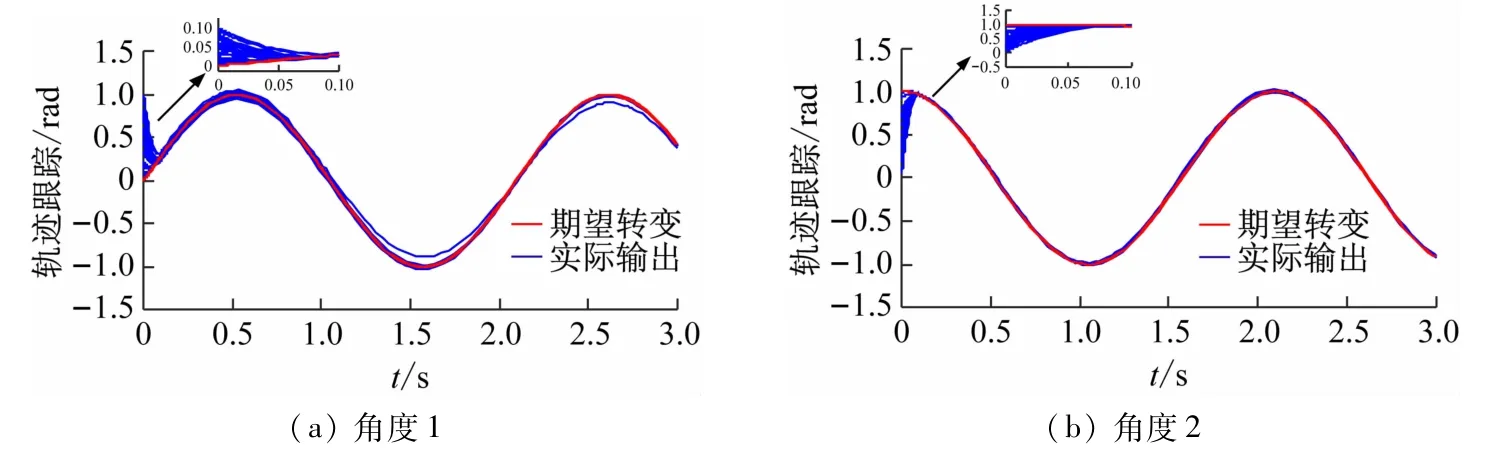
图3 20次迭代学习后关节角跟踪过程

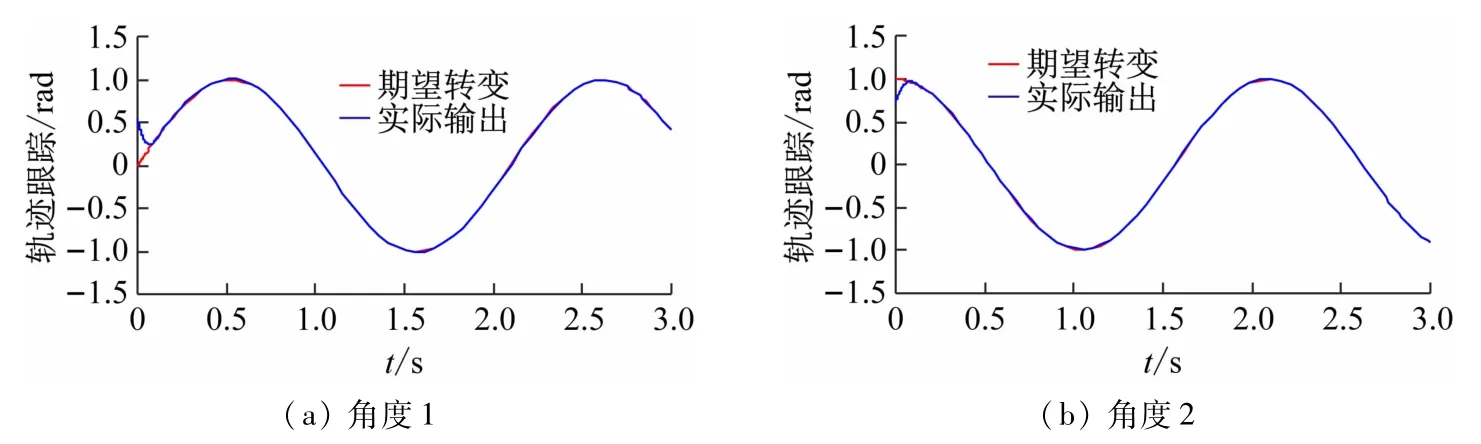
图4 第20次迭代学习的关节角跟踪

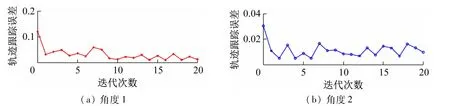
图5 20次迭代学习角误差收敛图

图5给出了控制器在20次迭代学习下关节角1、2在t∈（h／ak，T］时间段内轨迹跟踪误差收敛图。可以看出，随着迭代次数的增加，关节角1、2的轨迹跟踪误差在逐渐收敛。所提算法有效地抑制了随机初态误差对系统轨迹跟踪的不良影响。

4 结语

在非线性、强耦合的柔性机械臂系统轨迹跟踪迭代学习控制中，针对因柔性材质属性使得系统每次迭代初始状态不同，所造成的被控系统控制精度不够高的问题，提出了一种初态加速修正的PD型迭代学习算法，在时间轴上设计了一个随迭代次数而缩减的修正区间，通过在该区间内对初始状态偏差进行修正，有效地抑制了随机初态误差对系统轨迹跟踪控制的不良影响，实现了对期望轨迹的跟踪。