曲柄滑块控制的无人驾驶自行车设计与实现

刘佩佩，周亚丽，张奇志，徐鑫鑫

（1.北京信息科技大学自动化学院，北京 100192；2.北京沃普拉斯科技有限公司，北京 100086）

0 引言

平衡控制在航空航天、机器人直立控制、科研教学、控制理论研究及验证等方面有着广泛应用［1］。与无人驾驶汽车相比，无人驾驶自行车具有静态不稳定性和动态可稳定性，因此对自行车的运动特性和平衡控制的研究已经成为一个重要的研究领域［2］。1899年Whipple［3］首次运用数学方程描述自行车的运动行为，他将自行车简化为前轮、后轮、车架和车体前叉四部分，应用倒立摆模型导出了自行车围绕直立垂直平衡点的线性化运动方程，并提出了自稳定的概念。随着计算机时代的到来，越来越多的研究者借用计算机仿真等工具对复杂问题进行仿真和分析，由此开始了对无人驾驶自行车的深入研究。从国内外研究现状可以看出，学者们对无人驾驶自行车系统的研究主要集中在各种形式的配重调节器设计、车体结构分析和运动过程中车身平衡稳定性控制等相关方面，并取得了丰硕的成果。例如，一些学者［4-8］着重研究了增加配重或改变传统自行车原有结构对无人驾驶自行车平衡运动的影响，结果表明，增加配重调节器或者改变自行车原有结构可以扩大系统倾角的调整范围。而另有学者［9-13］则认为无人驾驶自行车无需添加配重调节装置，仅靠车把和车轮运动即可保持稳定平衡。此种方案驱动自由度较少，控制容易，但能否达到前者的倾角调整范围和效果还需进一步验证［14］。

本文将以上两种主流思路进行结合，各取所长，设计开发了一种由曲柄滑块机构控制的无人驾驶自行车系统。通过曲柄滑块机构控制车体的运动方向，同时配合配重块调节车体重心，最终实现直立平衡运动。本文所设计的无人驾驶自行车实验平台不仅有利于培养学生解决复杂工程问题能力，更具有广阔的实际应用价值。

1 结构设计与建模

1.1 曲柄滑块机构模型

本文设计一种由滚珠丝杠滑台、曲柄和连杆组成的曲柄滑块机构来控制车体的运动方向。图1所示，滚珠丝杆滑台由螺杆、螺母、滚珠和滑块组成，是将回转运动转化为直线运动，或将直线运动转化为回转运动的理想产品。由于摩擦阻力很小，同时具有慢速无爬行、高速无颤动的特点，滚珠丝杠被广泛应用于各种工业设备和精密仪器。可在高负载的情况下实现高精度的直线运动。

图1 滚珠丝杠滑台机构图

曲柄滑块机构模型简图如图2所示。记曲柄OA的长为r，连杆AB的长为l，当曲柄绕固定点O以角速度w旋转时，由连杆带动滑块B在水平槽内作往复直线运动，整个曲柄滑块机构通过滚珠丝杠实现进给运动。

图2 曲柄滑块机构模型简图

假设初始时刻曲柄的端点A位于水平线段OB上，曲柄从初始位置起转动的角度为θ，连杆AB与OB的锐夹角为β（称为摆角）。

取O点为坐标原点，OB方向为x轴上的坐标轴，用x表示滑块的位移，即OB边的长度。得到：

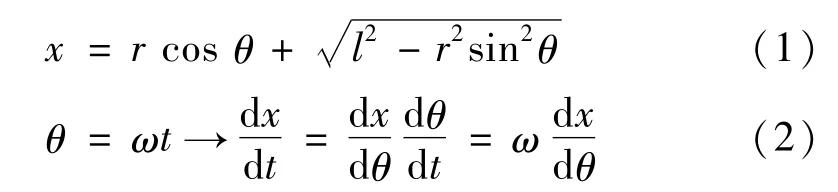
对模型进行近似化：因为（1＋ε）a＝1＋aε＋…，｜ε｜＜1。一般而言，r2／l2是远比1小的数，则滑块位移的近似模型为

1.2 无人驾驶自行车系统模型

图3所示为无人驾驶自行车系统三维模型图。整个系统可简化为由前轮、后轮、曲柄滑块机构以及车身框架组成。在当前研究阶段，配重块调整到一个合适的位置之后将其固定，可看成车体的一部分。曲柄滑块机构装配在车体横梁和前车把转轴上，通过伺服电动机驱动滑块在滑台上的移动控制自行车车把转动；附加配重块调节机构及控制电路安装在后车座上，可通过配重调节装置控制自行车重心平衡。

图3 系统三维模型图

图4所示为无人驾驶自行车系统结构模型图。自行车的前后轮与地面的接触点Q1Q2形成一条接触线，接触线与x轴的夹角为俯仰角Ψ，逆时针方向为正方向。W为自行车的轮间距，假设系统所有质量集中在质心上，定义质心高度为h，质心在水平面上的投影点A与Q2的距离定为b。车身与z轴的夹角为车体滚转角φ，顺时针方向为正方向［15］。通过滑块位置控制前轮转过的角度定义为方向角δ，如图5所示。定义车体滚转角和前车把转角均为零时的滑块位置为起始位置；起始位置时曲柄滑块机构可看成是一个直角三角形，定义直角短边为r（始终与前车把保持平行共面），直角长边为l，这两条边的长度为定值、可测量；定义滑块位置边长度为x。

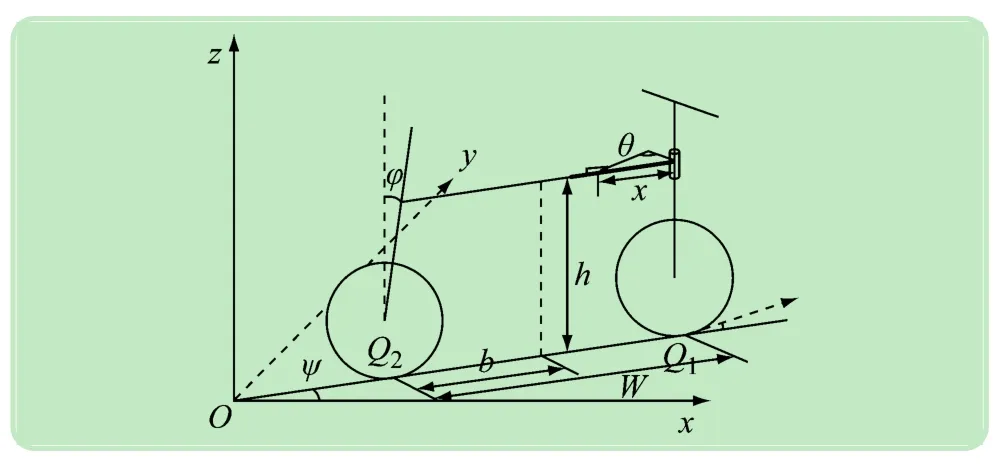
图4 无人驾驶自行车系统结构模型

图5 无人驾驶自行车系统结构俯视图

由图4 可知，δ＝90°－θ，代入式（3），得：2

当车体处于直立状态时，式中各角度均为极小量，则cos δ≈1，sin δ≈δ。

将式（4）进行线性化：

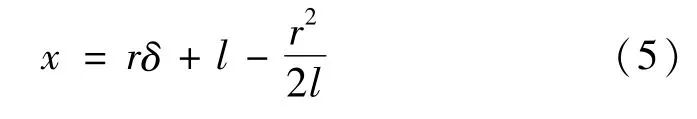
由式（5）得：

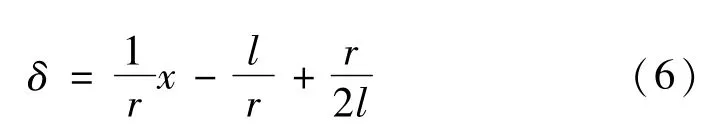
根据质点系相对于动轴的动量矩定理，可得系统线性倾斜动力学模型［16］：

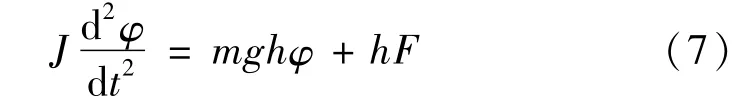
式中：J为系统相对于自行车轮间距的转动惯量，F为系统所受牵引惯性力，

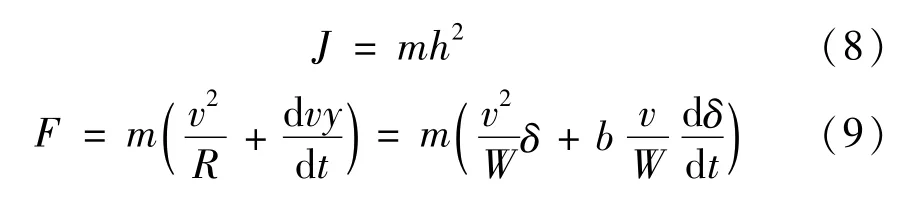
v为车体运动速度；R为车轮半径。

将式（8）、（9）代入式（7），得到以转向角δ为输入的自行车动力学模型：

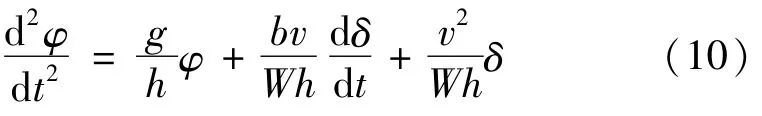
将式（6）代入式（10）得：

最终得到以曲柄滑块位置x为输入，以车体倾角φ为输出的单输入单输出无人驾驶自行车动力学系统模型。

2 电控系统设计

如图6所示为无人驾驶自行车电控系统图，主要包括：上位机（Intel NUC6i7KYK小型PC主机）；下位机（控制单元STM32）；伺服驱动单元（3个伺服电动机及伺服驱动器）；姿态传感器（MPU-6050）；OLED 显示屏；48V＠14AH锂电池组。

图6 无人驾驶自行车电控系统图

2.1 上位机

小型PC主机型号为Intel NUC6i7KYK，采用第6代Intel i7-6770HQ 的CPU，2.6～2.5 GHz四核六兆缓存，机身轻薄，易于携带和安装，可以满足无人驾驶自行车系统正常运行所需。NUC6i7作为上位机是整个系统的控制算法和信息处理核心，主要作用是将下位机发送过来的姿态信息（俯仰角、滚转角、偏航角、三轴陀螺的原始数据）进行帧协议解析，并将解析完的各电动机模块控制信息发送给下位机。

2.2 下位机

下位机以STM32作为控制核心单元，通过隔离USB转UART与上位机通信，通信速度1 Mb／s，物理线缆为一根USB2.0 A口线，直接插接到PC机USB口即可。通过I2C接口搭载MPU-6050姿态传感器、通过RS-485接口与伺服驱动单元通信、通过SPI接口外接一个OLED显示屏，可以动态显示程序运行状态和数据变量。

电控系统下位机的主要作用是接收上位机解析完成发送过来的各电动机模块控制信息，同时不断采集各电动机模块的编码器信息。

2.3 电动机及驱动单元

无人驾驶自行车系统驱动单元包括3个伺服电动机及伺服驱动器，分别是：控制自行车转速的转速电动机模块、控制自行车重心的平衡电动机模块、控制自行车车把的转向电动机模块。

平衡电动机和转向电动机型号为雷赛ACM4005V24H-B5，电动机内部集成有绝对式编码器，工作在位置模式，额定功率为50 W，额定转速为3 000 r／min，额定力矩为0.16 N·m；转速电动机为车体自带轮毂电动机，工作在速度模式，在电动机外部安装一个增量式编码器。3个电动机配套自行设计的Su7020三相交流伺服驱动器。

由于3个伺服电动机模块控制信号均通过RS-485总线通信，故需要对3个电动机模块进行编号，规定为：转速电动机模块ID＝01，平衡电动机模块ID＝02，转向电动机模块ID＝03。

2.4 姿态传感器

本系统采用InvenSense公司的MPU-6050高性能的三轴加速度计、三轴陀螺仪芯片来确定姿态位置，结构设计上要求控制核心板和系统平行安装，获取俯仰信息即为机构的俯仰信息［17］。MPU-6050集成了3轴MEMS陀螺仪、3轴MEMS加速度计，以及一个可扩展的数字运动处理器DMP（Digital Motion Processor），可用I2C接口连接一个第3方的数字传感器，比如磁力计或压力传感器。MPU-6050对陀螺仪和加速度计分别用了3个16位的ADC，将其测量的模拟量转化为可输出的数字量。为了精确跟踪快速和慢速的运动，传感器的测量范围都是用户可控的，陀螺仪可测范围为±250，±500，±1 000，±2 000°／s，加速度计可测范围为±2，±4，±8，±16 g。本系统参数设定为：陀螺量程：±2 000°／s，加速度计量程：±16 g。

无人驾驶自行车系统姿态传感器的功能为采集系统运动时的姿态信息，传感器输出信息主要包括：俯仰角、滚转角、偏航角、三轴陀螺的原始数据（传感器内部16 bit ADC采集数据）。

2.5 系统电源

整个系统使用48V＠14AH锂电池组供电，伺服驱动模块的供电为电池组电源48 V，并且通过急停控制固态继电器方式输出，摁下急停后所有电机会掉电卸载。上位机供电电压为19 V，所以需要DC48～19V模块转19 V输出，并在电源模块输入前级设计按钮开关。下位机电源使用24 V供电，与上位机电源并联，均使用19 V电源输入，故整个系统同时上电、掉电。

3 控制系统设计

3.1 系统操作界面设计

系统界面如图7所示，用于监控系统的运行状态。界面左边分别为打开端口、关闭端口和显示接收数据，中间可显示采集并解析完成的3个电动机的速度、位置等运动信息，界面右端可通过勾选“记录数据”将系统运动的各项数据记录下来并生成.text文件保存到指定路径，以便后需进行数据分析。

图7 无人驾驶自行车系统操作界面

3.2 系统控制算法设计

图8、9分别为无人驾驶自行车系统软件数据流程图及双闭环控制框图。

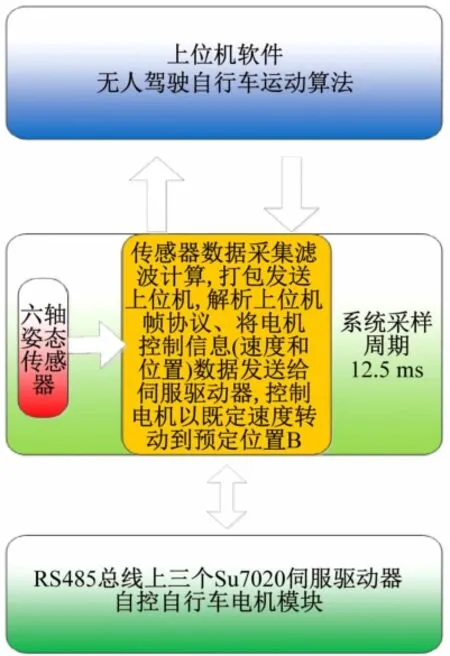
图8 系统软件数据流程图

图9 无人驾驶自行车系统双闭环控制框图

当系统启动运行后，上位机根据MPU-6050姿态传感器传过来的实时姿态信息（俯仰角、滚转角、偏航角以及三轴陀螺的原始数据）进行帧协议解析，解析后得到的各伺服电动机的速度和位置信息作为内环的期望输入值；伺服驱动模块根据上位机发送过来的各电动机速度和位置信息，经反馈闭环调节，分别控制3个电动机去执行相应任务。同时不断采集调整后的姿态信息判断整个系统是否达到了平衡状态。

4 试验验证

4.1 样机安装与调试

图10为曲柄滑块机构实体装配图，轴承选用进口IKO鱼眼接头轴承，此曲柄滑块机械结构具有控制精确，力矩大和操作简单的特性。图11和图12分别为样机左视图和俯视图，配重调节装置由滚珠丝杠滑台和5个配重块组成，每个配重块0.98 kg。曲柄滑块机构和配重调节装置的滑台总长均为38 cm，丝杠螺距0.37

cm。系统的核心控制电路安装在配重调节装置后方的车架上，样机总质量为38.95 kg，无人驾驶自行车系统的相关物理参数为：曲柄连杆直角短边r＝102.8 mm，曲柄连杆直角长边l＝272.2 mm，滑台丝杠螺距s＝3.7 mm，自行车车轮半径R＝0.185 m，自行车前后轮间距W＝0.94 m，质心投影到后轮距离b＝0.37 m，车体质心高度h ＝0.5 m，车体前向速度v＝0.8 m／s，重力加速度g＝9.8 m／s2，系统总质量m ＝38.95 kg。

图10 曲柄滑块机构实体装配图

图11 样机左视图

图12 样机俯视图

4.2 样机试验

图13所示为样机试验部分视频连拍图，每张图片的右下角为拍摄时间，为展示控制细节，每隔1 s采集2帧画面。

图13 样机试验视频连拍

首先在系统操作界面左边点击“端口设置”里的“打开”按钮，等待界面显示“成功打开自行车端口”之后，打开自行车样机上的启动按钮，完成所有准备工作之后将系统在无外力干预情况下自由释放。

图14所示为样机试验中测量得到的车体方向角δ和滚转角φ随时间变化的曲线。从图14可以看出，将自行车由方向角为0.075 rad（4.27°）、滚转角为0.02 rad（1.15°）的初始状态自由释放，在大约1 s时，车体方向角达到最大值0.54 rad（30°）；自行车自主行走大约2 s后，曲柄滑块控制着车把开始在小幅度范围内调整；大约3 s时，因路面稍有不平，系统出现微微震荡，但0.2 s后迅速调整回稳定状态，之后系统便维持动态平衡运行。

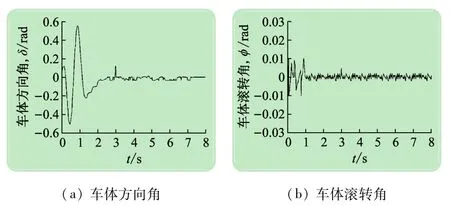
图14 样机试验结果

样机试验结果表明，本文所设计的由曲柄滑块机构控制的无人驾驶自行车系统可以在水平路面上实现稳定直线运动。

5 结语

本文设计开发了一种由曲柄滑块机构控制的无人驾驶自行车系统。依次进行了动力学建模、电控系统设计和软件系统设计，采用双闭环控制思想进行了系统控制器的设计，并进行了样机试验验证。多次样机试验结果表明，曲柄滑块机构对前车把方向的控制精确、快速且操作简便，采用传统简单的双闭环控制算法即可实现试验样机在水平路面上的稳定直线平衡运动。