积累活动经验 建立数学模型

蒋媛 孙冬梅

【摘 要】从学习心理的角度来看，推理往往是指由一个或一个以上的概念，推理出新的判断的过程，这个过程不仅常见于教学当中，也常常存在于生活当中。数学模型有助于学生将具象抽象化并进行解释和应用。在推理中建立数学模型，让学生在操作中经历，在经历中体验，在体验中累积，这样才能获得最具数学本质的、最具价值的数学活动经验。

【关键词】演绎推理 归纳推理 合情推理 数学模型 活动经验

在动手操作中学数学，有利于学生经历“动作思维—表象—抽象思维—概括—形成模型”的过程。因此在教学中，组织学生实践操作，参与推理的全过程，引导思维由直观向抽象转化，从事物中发现规律，进行归纳，形成模型。数学推理的类型有很多，下面笔者从演绎推理、归纳推理和合情推理这三个方面，谈一谈关于“长方体和正方体的整理和复习”的一些思考。

一、从演绎推理中建立数学模型

演绎推理又称为论证推理，是根据已有的事实和正确的结论（包括定义、公理、定理等），按照严格的逻辑法则得到新结论的推理过程，是从一般到特殊的推理，它是以某类事物的一般判断为前提做出这类事物的个别、特殊事物判断的推理方法。

【案例】怎样拼表面积最小

师：把2个这样的盒子用纸包装起来，怎样拼最省包装纸？为什么这样拼？

生：把最大的面重叠起来，表面积最小。

师：把两个小长方体拼成一个大长方体，都减少了几个面？

（指出：两个纸盒拼起来表面积少了2个面）

师：如果再增加一个长方体呢？怎样拼表面积最小？你为什么这么拼？

生：把最大的面重叠起来，表面积最小。

师：减少了几个面？

（指出：拼接一次，重叠2个面，拼接2次，重叠4个面）

师：通过将2个、3个小长方体拼成一个大长方体，你有什么发现？

（指出：重叠的面越大，表面积越小）

师：猜猜看，如果要将4个纸盒拼起来，怎么包装最省包装纸？

（追问：这种实际上大大小小重叠了几个面？重叠了哪8个面？）

师：还有小组是这样拼的，重叠了几个面？（展示其他两种拼法）都是重叠了8个面，你认为一样吗？哪种重叠方法表面积最小？

（指出：重叠的面越多、越大，表面积越小）

师：现在你能用这种方法，研究怎样包装6个纸盒最省包装纸了吗？6人小组合作拼一拼，并在小组里说一说为什么这样拼。

师：其实我们生活中很多物品的包装就是采用的这种拼接方法。

师：刚刚我们拼了2个、3个、4个和6个小长方体，你发现了什么奥秘？

（指出：我们在拼小长方体时，发现重叠的面越大、越多，表面积就小）

师：刚才我们研究了长方体，正方体是特殊的长方体，那正方体中是不是也有这样的规律呢？

（指出：正方体是特殊的长方体，长方体的规律，对于正方体也是成立的）

师：那正方体的规律有什么特殊的地方？

（指出：正方体的每个面都相等，表面积最小的时候只要考虑重叠的面越多就行了）

【思考】学生在拼2个和3个的小长方体的过程中积累了一些活动经验，知道了将最大的面重叠起来，表面积最小。因此在拼4个小长方体的时候很容易就将经验迁移过来，这是学生的思维定式。因此让学生通过再次操作，有了和前面不一样的发现，而这个发现是对前面经验的补充，从而推理出结论并建立起“重叠的面越多、越大，表面积越小”这一模型。而正方体是特殊的长方体，通过一般事物的模型，推理出特殊事物的模型，是演绎推理的范畴。演绎推理认为：前提与结论之间有着必然的联系，只要前提是真的，推理是合乎逻辑的，就一定能得到正确的结论。因此可以推理出正方体也同样适用，但有着特殊的地方，每个面的大小一样，只要考虑重叠的面最多就可以了。让学生参与推理的全过程，从中积累数学活动经验。

二、从归纳推理中建立数学模型

归纳是由个别到一般的推理，从特殊事实得到一般原理，即通过一些学生熟知的个别生活实例或数学问题，再进行观察，比较、分析、综合中归纳出一般结论。

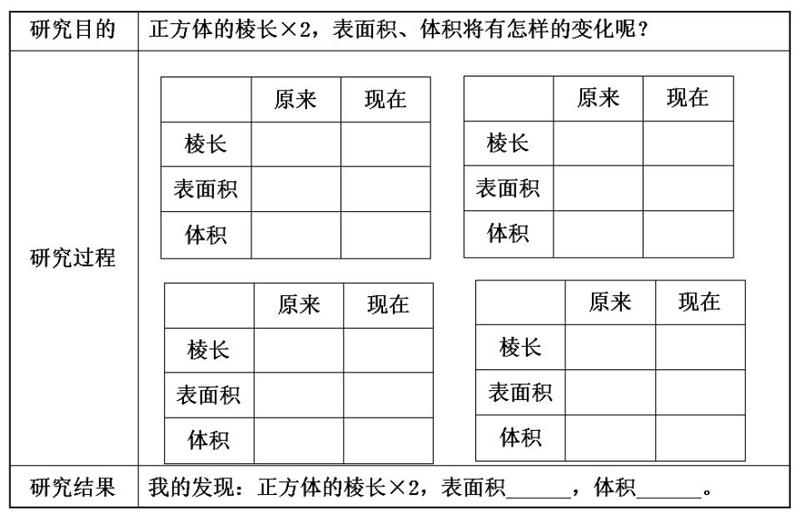
【案例】正方体的棱长乘2，表面积和体积将发生什么变化？

师：如果正方体的棱长乘2，那表面积和体积将有怎样的变化呢？我们一起来研究研究。

要求：1.每人拿出表格独立填一填。

2.组长将每人的表格贴至学习单上，小组讨论并完成“我的发现”。

小组展示学习单，组长汇报研究的过程。

师：你们的发现和他们一样吗？是不是任意的正方体只要棱长乘2，都有这样的规律呢？

4人小组讨论，写出验证过程。

组长汇报，师指出：通过验证，我们发现当正方体的棱长乘2时，表面积乘4，体积乘8。

【思考】数学知识是抽象的，而小学生的思维是以形象思维为主的。显然，数学学科的特点与小学生的思维特点是矛盾的。所以在小组合作的过程中，学生可以观察小组内举例的直观数据进行初步猜想，在全班讨论时，如果每人举例都不一样，也仅仅只有50多个表象，不能涵盖所有，那这一猜想到底正确与否就要我们去验证。怎么验证才能够涵盖所有？才能由具象到抽象呢？用字母a表示正方体的棱长，建立模型。由于前面已经有了大量的表象作为基础，并且学生已经积累了一些数学活动经验，得到了具象的结论，在此基础上归纳出模型是完全能够实现的。同时在这一活动中，学生由浅及深、由具体到抽象积累了数学活动经验。

三、从合情推理中建立数学模型

合情推理是根据已有的知识和经验，在某种情景和过程中推出可能性结论的推理，主要包括观察比较、不完全归纳、类比猜想、估算联想。在教学中如何进行合情推理能力的培养，使学生能够学得轻松有效，循序渐进，培养创新精神，是一个值得我们深思的问题。

【案例】正方体的棱长×n，表面积和体积将发生什么变化？

师：猜一猜，如果正方体的棱长乘了3呢？表面积和体积又怎样变化呢？

生：表面积乘了9，体积乘了27。

师：如果乘4了呢？你有什么发现？

生：表面积乘了16，体积乘了64。

师：你发现了什么？

生：表面积乘了平方倍，体积乘了立方倍。

师：如果正方体的棱长乘了n，表面积乘了n2，体积乘了n3。这仅仅是猜想，你有什么方法验证吗？4人小组讨论，验证过程写在学习单的反面。

師：看来我们刚刚的猜想是正确的。

师：那任意一个长方体是不是也有这样的规律呢？我们可以借助刚刚研究正方体的经验，课后继续研究。

【思考】数学是在人们对客观世界定性把握和定量刻画的基础上，逐步抽象、概括，形成模型、方法和理论的过程，这一过程充满着观察、猜想和合情推理。接着让学生猜想棱长乘3、乘4，表面积和体积怎样变化，最后让学生猜想任意一个长方体是不是也有这样的规律，并让学生对照自己的猜想进行验证，完善修改。然后加以类比，这一系列的过程，都是合情推理。因此再次让学生学习时，用字母代表了棱长，并且让学生在推理中得出“正方体的棱长乘了n，表面积乘了n2，体积乘了n3”。最后让学生研究由特殊到一般，将研究正方体的方法延伸到长方体，看是否也存在这样的规律。这两个数学活动都体现了合情推理和模型的有效结合。

让学生在操作中推理，在推理中建模，这样才能获得最具数学本质的、最具价值的活动经验。