海上风机筒型基础-场地动力响应的试验及模拟研究

王雪菲，马成良，李家乐

海上风机筒型基础-场地动力响应的试验及模拟研究

王雪菲1, 2，马成良1, 2，李家乐1, 2

(1. 河北工业大学土木与交通学院，天津 300401；2. 天津市装配式建筑与智能建造重点实验室，天津 300401)

筒型基础作为海上风机的一种新型基础结构，具有安装方便、重复使用、成本低等显著优点．在地震荷载作用下，地基土可能发生液化，液化后砂土的强度和刚度会降低，导致地基承载能力下降，筒型基础可能发生过大竖向沉降，严重威胁风机的运行．针对筒形基础影响范围内土体的地震响应规律，本研究开展了一系列离心机试验，记录了筒体周围砂土地基加速度、孔隙水压及沉降的时程曲线．基于OpenSees开源平台进行了一系列数值模拟工作，揭示了土体的应力、应变、孔压等动态响应，通过对试验超静孔压比结果的校正验证了数值计算模型的可靠性，进而分析了基础与土体相互作用下地基的液化规律及筒型基础尺寸效应对抗液化性能的影响．研究表明，上部荷载增加了地基中的附加应力，使筒下和筒周围的土体具有较好的抵抗液化能力；由于筒型基础内部土体的排水路径较长，筒内土体的孔隙水压力消散较慢，数值与同一深度筒外土体的孔隙水压相比偏大；筒型基础的抗液化能力随着高径比的增大而呈削弱趋势；在深度方向上现筒下的超静孔压比在筒型基础底部附近达到极小值，研究成果旨在为不同地震设防等级的地区提供设计依据．

筒形基础；离心机试验；超静孔压比；附加应力；地震

过量碳排放量导致的一切环境问题越来越引起人们的关注，亟待解决，发展海上风电是节能减排和能源转型发展的需求，风电是新能源的主要发展方向，受到国家的大力扶持[1-3]，到2020年我国海上风机装机容量将达5000MW以上[4]．中国发展海上风电的优势有风电资源丰富、海岸线悠长，同时风机发电量高、运行比较稳定、不占陆地资源．但海上风机的建设成本过高是制约发展的重要因素，筒形基础作为一种新型的风机基础具有满足成本要求的优势[5]，如何保证其运行期间不发生0.5%的倾角并具有足够的抵抗液化能力是当前需要解决的问题．筒形基础的安装方式使其不能具有较深的入土深度，与浅基础的承载特性相似．中国地处最活跃的两个地震带之间，在地震荷载作用下提高筒形基础场地土体抵抗液化的能力备受关注．

陈育民等[6]利用FLAC3D二次开发了液化流动本构模型．Yu等[7]进行了重力基础的离心机振动台试验，得出了结构下的超静孔压比与自由场中相比明显降低的结论．Wang等[8-11]通过一些列离心机试验研究了海上风机基础在地震作用下的动力响应．刘国威[12]构建了筒形基础海上风电系统有限元模型，对加速度、位移等动力响应参数进行分析，采用抗液化剪应力方法分析了地基的液化趋势．杨春宝等[13]通过OpenSees开源平台进行了海上风机吸力筒基础的三维动力数值计算，对基础在地震中的沉降变形和倾覆转角进行了描述；刘润等[14]在饱和砂土地基上开展了轻型和重型筒形基础的离心机振动台试验，根据测得的加速度和孔压响应分析出了筒形基础对砂土的孔压比累积存在抑制作用，提出了提升比的判别方法来量化定义筒形基础附加应力对提高砂土抗液化的能力．于通顺等[15]基于Abaqus对宽浅式的筒形基础进行了模拟，结果表明在基础附近海床液化深度与水深、饱和度、渗透系数成正比，与土体的泊松比成反比．De Risi等[16]探究了海上风机在强震作用下的结构性能．Ueda等[17]进行了100的离心机模型试验并基于数值模型计算对筒形基础作用下的土体有效应力进行了分析，研究了其抗震性能．目前基于离心机振动台国内外学者已经做了大量关于筒型基础在地震荷载作用下抵抗液化的性能试验，但是限于传感器的数量针对不同类型筒形基础的场地动力响应变化规律的研究较少．

土工离心机利用超重力原理可以使用小尺寸模型实现对原型土工结构的反应参数的模拟，主要的应用领域有土石坝稳定与变形、波浪模拟、爆炸模拟、地震及液化模拟．关于筒型基础作用下砂土抵抗液化的影响规律大多就是基于离心机振动台试验，Wang等[11]使用凯斯西储大学的20g-ton岩土离心机对海上风机基础进行了大量的离心机试验，总结了筒形基础作用下砂土地基关于自由场、筒周、筒下土体的液化规律．基于离心机试验对比验证，本研究利用OpenSees开源平台开展一系列数值模拟计算，分析地震载荷作用时筒形基础对土体抵抗液化能力的影响规律，揭示了地基土体位移、孔压、孔压比随深度和宽度的变化规律，提出了地震作用下不同高径比的筒形基础与砂土地基相互作用的动力响应规律．

1 离心机试验及数值建模

1.1 离心机试验

本研究中开展了一系列离心机模型试验，研究在地震载荷作用下海上风机筒型基础的动力响应及场地液化情况．试验筒型基础模型外径30m，风机塔柱高13m，上部结构简化为一个作用于塔柱顶部的集中质量块，重量为710t，模型具体尺寸如表1所示[18](原型尺寸)．离心机试验用土选用Toyoura砂，砂土参数见表2，试验是在饱和状态下开展的，地震载荷在离心加速度达到50时施加于模型箱底部，输入地震波主频率为2Hz，在模型最底部沿水平方向施加，峰值加速度为3.5m/s2，持续时间约为12.5s，如图1所示[19]．试验中记录了加速度、孔隙水压及基础沉降的时程曲线，用于描述地基土体地震响应．具体试验步骤在文献[11]中有详尽描述．

表1 试验模型尺寸

Tab.1 Configuration of the test model

表2 试验砂土材料参数

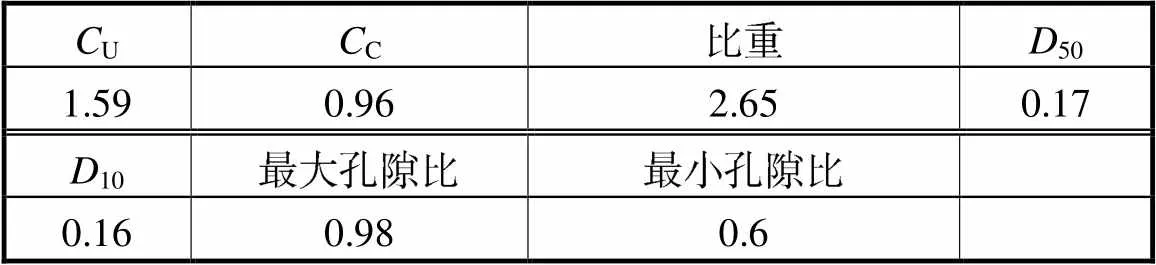
Tab.2 Parameters of test sand

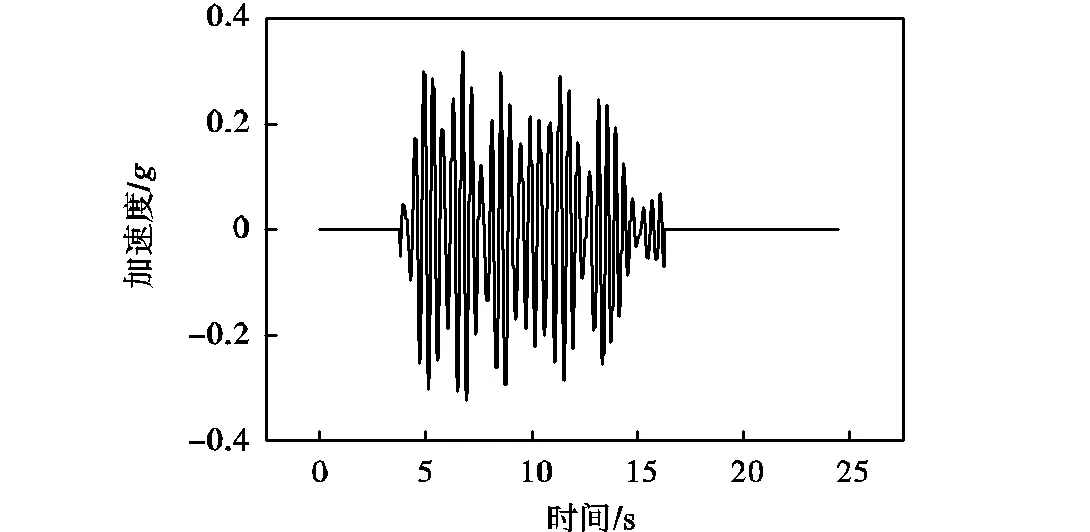
图1 输入地震加速度

1.2 有限元模型

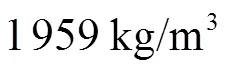
图2 桩土界面连接示意

图2中，零长度单元节点在二维模型中只有2个自由度，而桩节点和土体节点有3个自由度，本文在不同自由度节点间通过equalDOF命令连接起来．桩土间的摩擦系数取0.3．摩擦力计算公式为

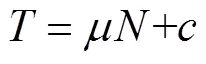
土体底部单元底部边界通过fix命令固定水平和竖直方向位移，左右边界同一高度的节点通过equalDOF命令连接在一起模拟土体在震动过程中的剪切变形，上部边界设置为自由排水．在试验中，在饱和砂土上方有1.5m深的上覆水层，为了在不改变土壤单元有效应力的情况下纳入场地上覆自由水的动态影响，在水体下方网格边界上的每个节点使用质量命令分配一个节点质量．本文中土体表面水平，所以水平质量设置为零，垂直质量设置为节点“支持”水的体积质量．对于每个节点，其体积以节点上的水深、到相邻节点的距离的一半和单元的厚度为界．根据土体划分单元的尺寸，对节点进行水平和垂直质量的分量分配．

模型从单一变量原则考虑设计了3个模型尺寸，本研究主要目的是通过对比不同高径比的筒型基础在地震过程中的土壤液化规律，研究几何尺寸对筒型基础地震响应的影响规律．3个模型保持直径不变，改变筒高，详细信息如表3所示．为减小边界效应的影响，本研究中地基宽度取10倍的筒径，模型安放在地基的中心位置．

表3 数值模拟筒型基础尺寸

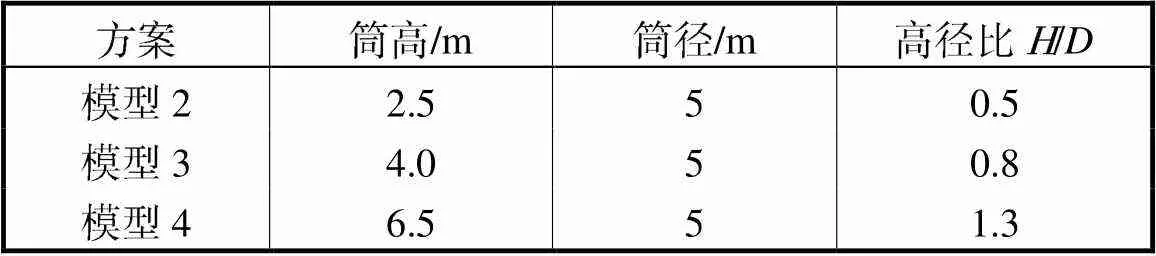
Tab.3 Dimensions of simulated bucket foundation

OpenSees数值模拟分析中测点布置如图3所示，方形标块是自由场位置测点；圆形标块是筒形基础周围位置测点；x形标块是筒形基础筒下位置测点．测点从上到下的深度位置在标块右侧给出，下面的分析都是基于这些测点进行的．同时规定了同一标块组成一条路径，从左到右分别命名为路径1、路径2、路径3．

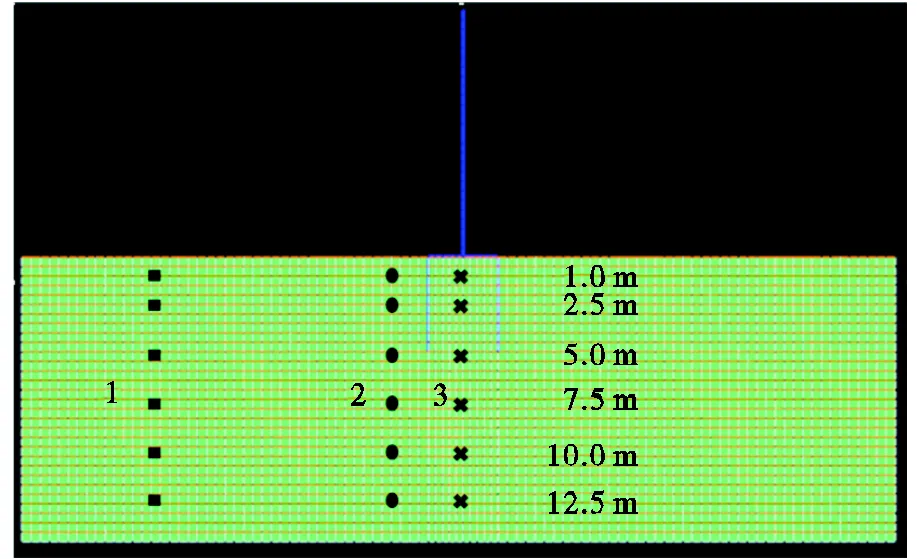
图3 测点位置

2 数值模型验证

图4为离心机振动台试验(图4(a))和OpenSees数值模拟计算(图4(b))得到的超静孔压比的时程曲线，选用高径比为1.3的筒型基础，分析了2.5m埋深处筒下、筒周以及自由场的超静孔压在地震载荷施加前后的变化趋势．对比结果表明，离心机试验及数值模拟分析揭示的地基土体液化性能一致：自由场处的超静孔压比大于1.0发生初始液化，而筒周和自由场处超静孔压比均未达到1.0未发生液化，筒周桩土摩擦和筒下附加应力提高了初始竖向应力，加强了地基土的抗液化性能．数值模拟计算中得到的3个采样点的超静孔压比峰值均与试验较吻合，有效揭示了在筒型基础作用下地基土体的抗液化性能，数值模型得到验证．通过进一步对比可知，试验得出的孔隙水压较数值计算消散速度更快，在地震载荷结束后即发生明显下降．在离心机试验中采用蒸馏水作为饱和液体介质，根据离心机相似比，离心机试验中孔压的消散速率与时间成二次方的关系，导致试验中孔压消散较快．

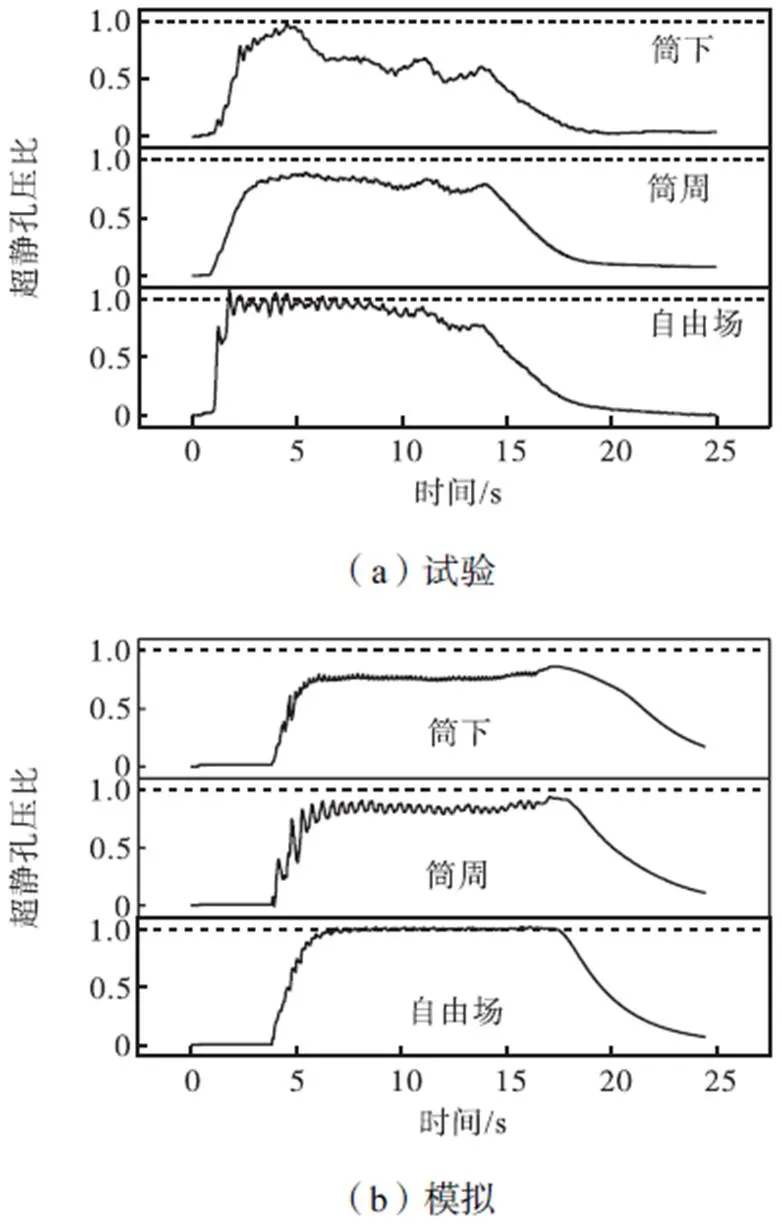
图4 超静孔压比对比

3 模拟结果反应分析

3.1 侧向位移

3种模型在地震期间筒前表层土体的侧向位移时程曲线如图5所示，数值分析中共选取了距离筒中心为1倍、2倍、6倍半径处的3个点进行对比．结果表明，在地震荷载作用下，筒模型前方表层土体均发生水平位移，位移在3个测点以不同的增长速率进行累积最终趋于稳定达到峰值，在距离筒形基础中心距离较近时，土体发生较大的侧向位移，距离较远处土体侧向位移数值较小，这个现象在较大外部载荷作用下更加明显，如图5(d)所示．对比不同高径比的筒型基础模型可知，在固定筒型的条件下，地基侧向位移趋于随埋深的增加而减小，高径比较大的筒型基础能够较好地抵抗侧向位移，拥有较高的水平稳定性．

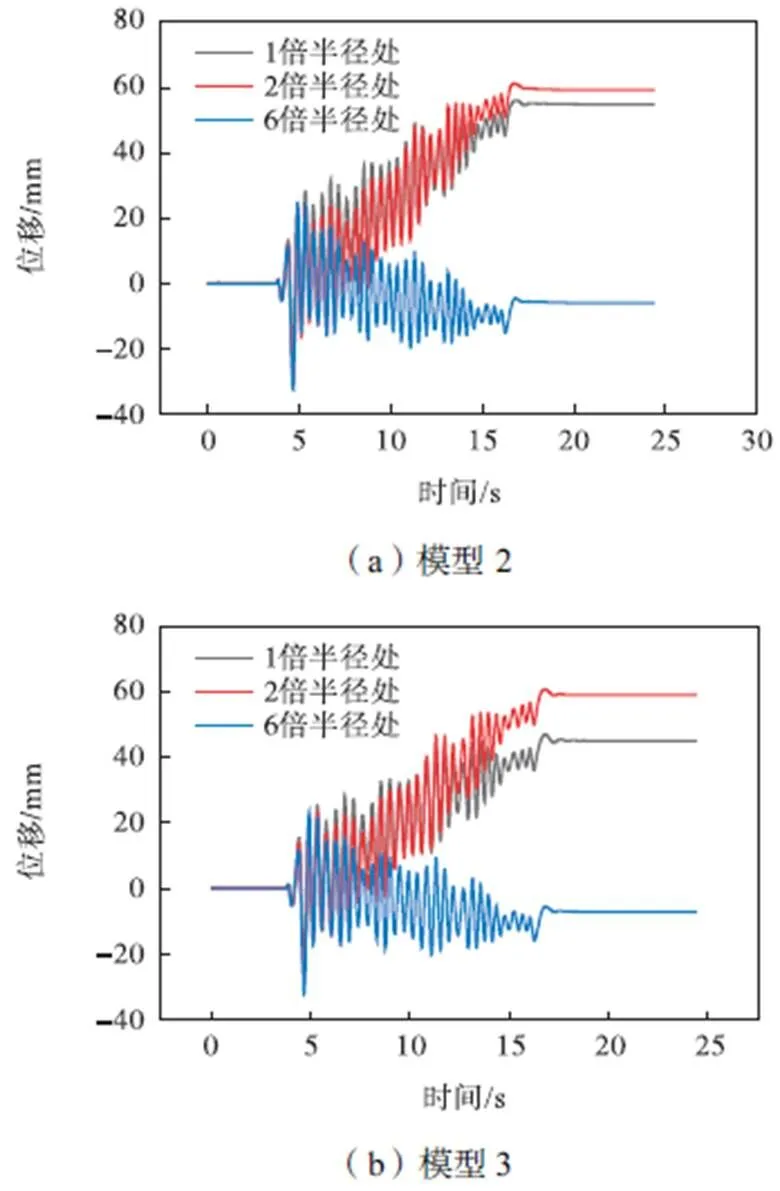
图6显示了3种模型地震过程中的转角时程曲线，荷载作用下因为土体承载能力的弱化，筒基发生转角并在震中不断累加，地震后期累计变形有减缓的趋势，最终导致转角大于规范规定的要求．在朱斌 等[20]的论文中提到中国FD003—2007试行规范规定高度大于100m的风电机组基础转角不大于0.17°；英国在Thornton Bank海上风电场中规定重力式基础的转角不大于0.25°；德国规定海上风机的基础转角不大于0.5°．其中模型2的转角最大，达到了0.632°，说明在地震载荷作用下高径比较小的“矮胖型”筒基抵抗倾覆的能力较差．模型3、模型4的转角相差不大，但模型3产生的转角相对较小，说明增大高径比可以提高筒基的侧向承载力，但是高径比过大高瘦型筒基对动态荷载作用下侧向承载能力的提升不再那么明显，在3个模型中以模型3表现最佳．

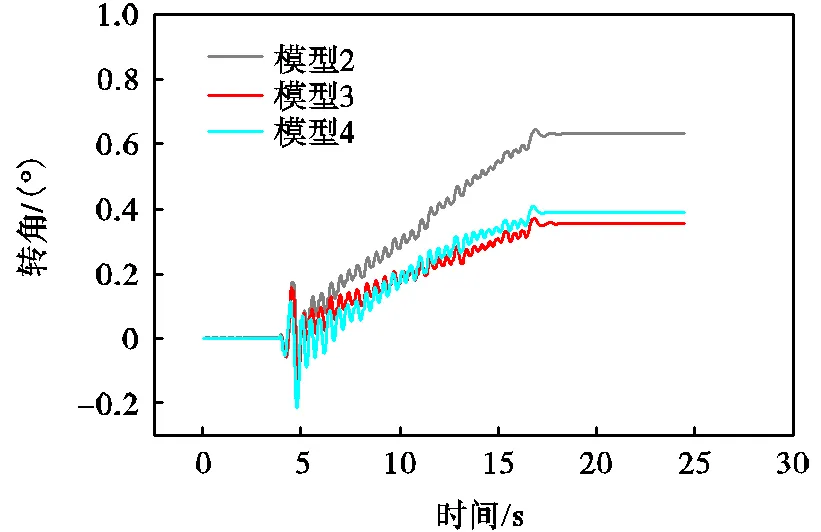
图6 转角时程曲线

3.2 场地孔压

地震过程中，地基中孔隙水压力的上升导致地基出现液化，进而导致基础发生较大的竖向沉降威胁风机的正常运行．孔隙水压的分布对不同尺寸基础的抗震性能也有较大的影响．图7显示了各阶段的孔压分布云图，其中图7(a)为地震前的静水压力分布情况，图7(b)为地震过程中孔隙水压力上升阶段(12.22s)的孔压分布，图7(c)为地震结束时孔隙水压消散过程中的孔压分布．地震中随着孔压的上升，土体的有效应力变小，导致筒内产生较大的水头压力，水力梯度变大，出现筒内的孔隙水压大于筒外水压的现象，地震结束后，孔压开始消散，筒内水压消散较慢．由于筒内场地孔压的变化规律相似，为了节约篇幅取模型2为例．

2.5m、1.5m、1.0m深度的相同位置处各3个测点位置的孔压时程如图8所示．发现3个位置的孔压消散速度不同，由于筒内排水路径比较长，所以孔压的消散速度最慢而且深度越浅消散速度越慢，其次筒周受其影响孔压消散速度也要慢于自由场．Wang等[11]的离心机模拟实验中的发现也是一致的规律，再次从孔压消散速度方面验证了模拟的可靠性．同时也可以发现，由于液化使得筒内压强水头增加，导致同一深度筒内的孔压往往高于筒外．

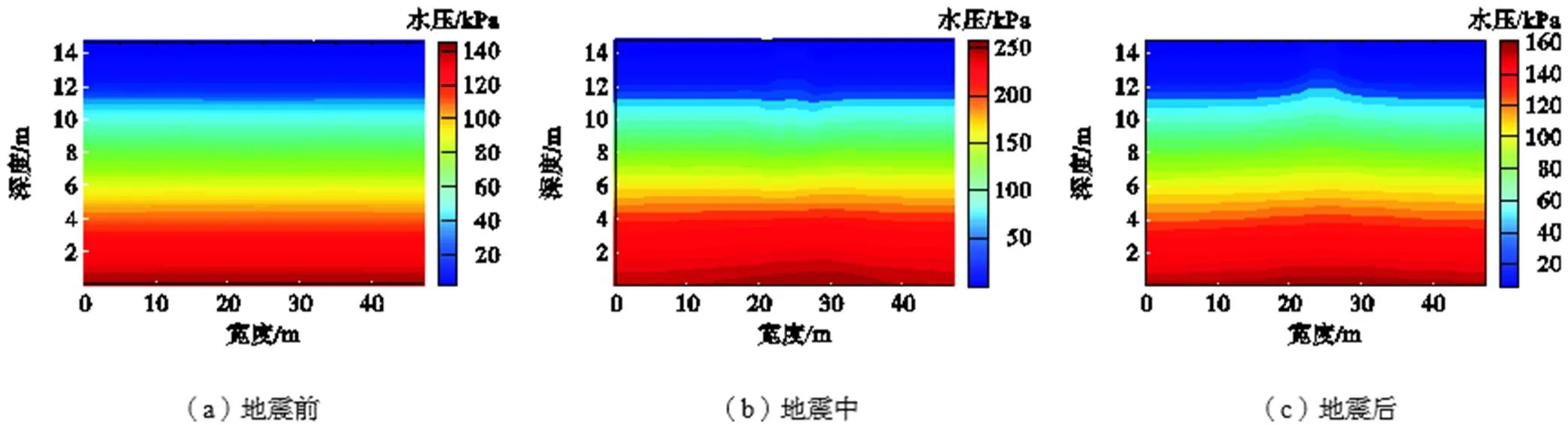
图7 地震各阶段孔压分布

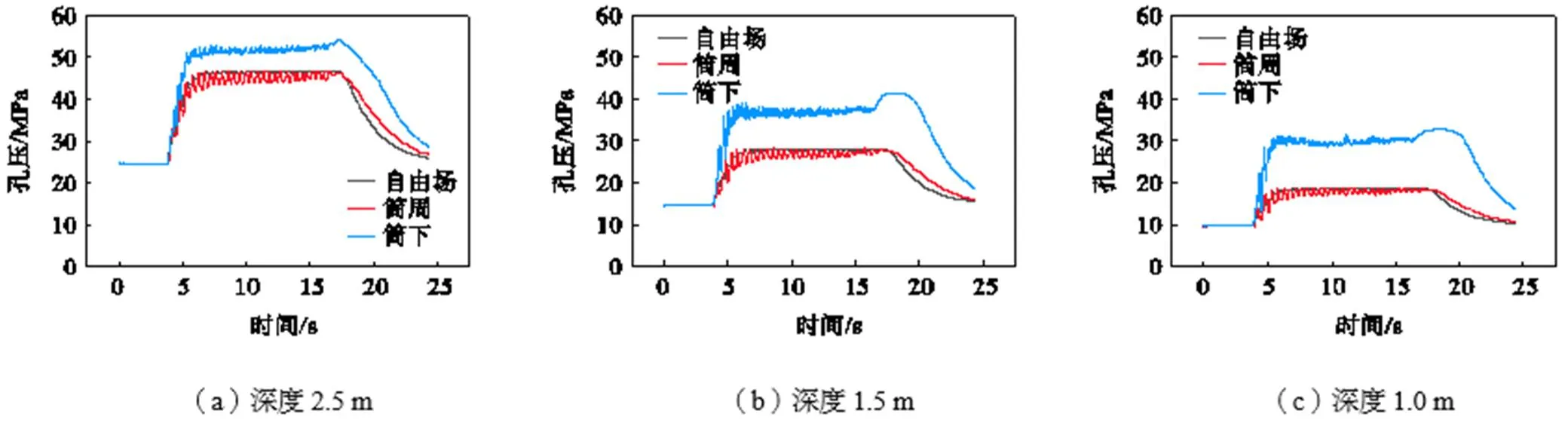
图8 孔压时程

3.3 液化判别及超静孔压比

本研究采用的液化准则为循环流动性准则，从液化的应力状态出发，当饱和土体中的超静孔压首次等于上覆土体的有效竖向应力时，即发生初始液化．在随后的振动荷载作用下液化现象周期性出现．超静孔压与土体有效竖向应力的比值，即超静孔压比为评价土体液化的指标．其中，超静孔压的大小与渗流路径和深度有关，有效竖向应力与基底附加应力的大小和深度有关，二者的变化规律决定了超静孔压比的变化规律，进而影响了土体抵抗液化的能力．超静孔压比的计算公式为

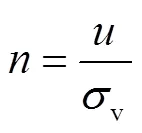
图9～11中显示了不同深度孔压比的时程曲线，图9为3种模型在自由场不同深度处的超静孔压比时程曲线，3种模型的时程曲线近似重合．通过对比可知，在深度5.0m范围超静孔压比接近1，砂土地基已经达到液化状态，超静孔压比随深度的增加而减小．图10为3种模型在筒周不同深度处的超静孔压比时程曲线，通过与图8对比发现在液化深度影响范围内3种模型均未达到完全液化状态，这是因为桩土之间的摩擦力和基底的附加应力提高了土体的竖向应力，提高了桩侧土体抵抗液化的性能．但同时3种模型的抗震性能在路径2(见图12)上发生了差异，随着高径比的增加，桩侧土体的抗震性能变差而且这种差异会随着深度的增加而消失；图11为3种模型在筒下不同深度处的超静孔压比时程曲线，通过对比发现其与桩侧土体的变化规律类似，在筒内随着桩径比的增大，相同深度的土体的液化趋势更明显，加大筒高不会提高筒内土体的抵抗液化的性能反而会使之降低；对比可知，筒基底部附近的土体抵抗液化的能力会提升，通过对比显示模型4土体超静孔压比＞模型3土体超静孔压比＞模型2土体超静孔压比．对比图9～11可发现，3种模型在深度12.5m处的超静孔压比一直没有出现过大差异，说明相同上部重量的筒形基础改变桩径比不会对较深处土体的抗液化性能有显著影响．

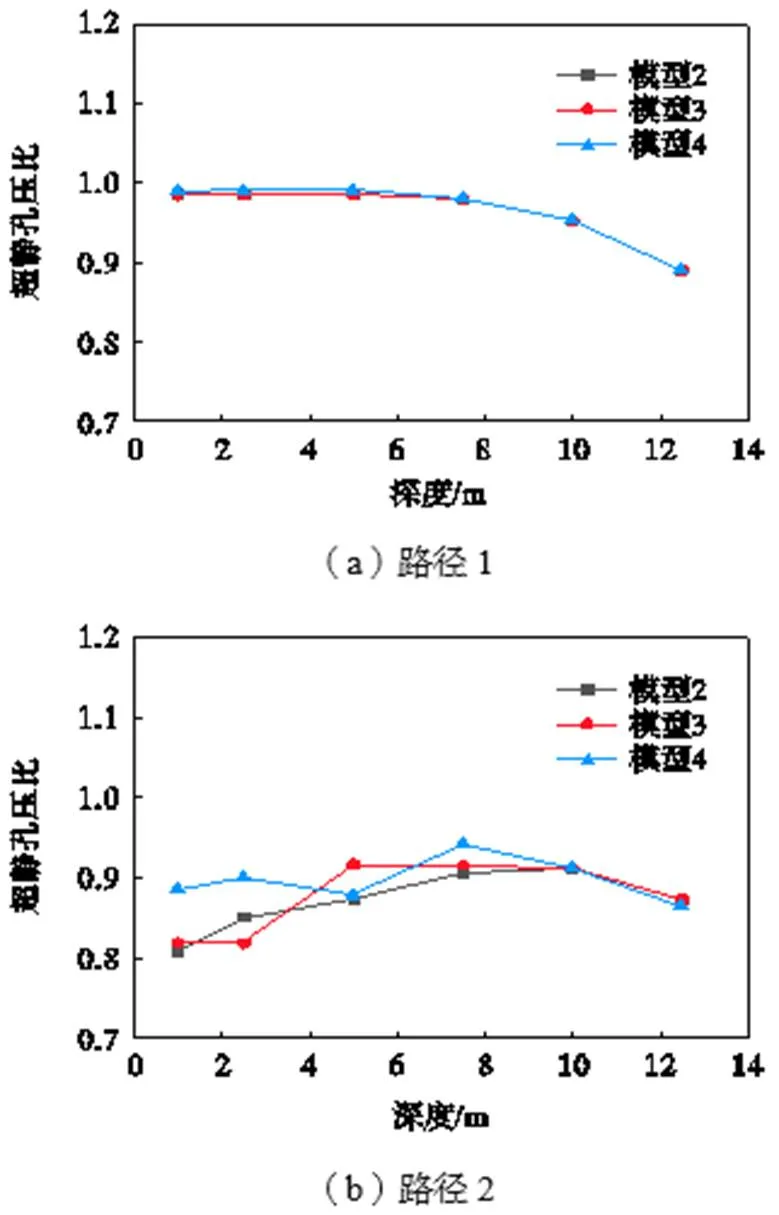
为了解超静孔压比随深度的变化趋势，将各模型孔压比峰值在沿不同深度路径的变化趋势列于图12．在路径1上超静孔压比先维持一个稳定数值1，表明地基发生了液化，之后随着深度的增加数值变小；路径2上超静孔压比随深度的增加呈现先增大后减小的变化，在深度8m时达到峰值；在路径3上超静孔压比的变化趋势比较复杂，将其分为3个阶段. 阶段1，在筒内超静孔压比随深度的增加而减小，出现了与较深处自由场变化规律相同的现象，这是因为筒内排水路径较长、附加应力较大并且没有扩散，这与自由场土体较深处的受力情况类似；阶段2，在离开筒之后超静孔压比在一段深度内随深度的增加而增大的现象，与自由场土体超静孔压比变化规律相反，这与刘润等[14]通过离心机振动台试验发现的模型筒下土体的超静孔压比随埋深的增加而增大的规律是一致的；阶段3，随着埋深的继续增加，超静孔压比随深度的增加而减小．高径比的增加使得阶段2的持续深度越来越小．这是因为大的高径比筒基底部土体应力较大，附加应力产生的影响相对较小．

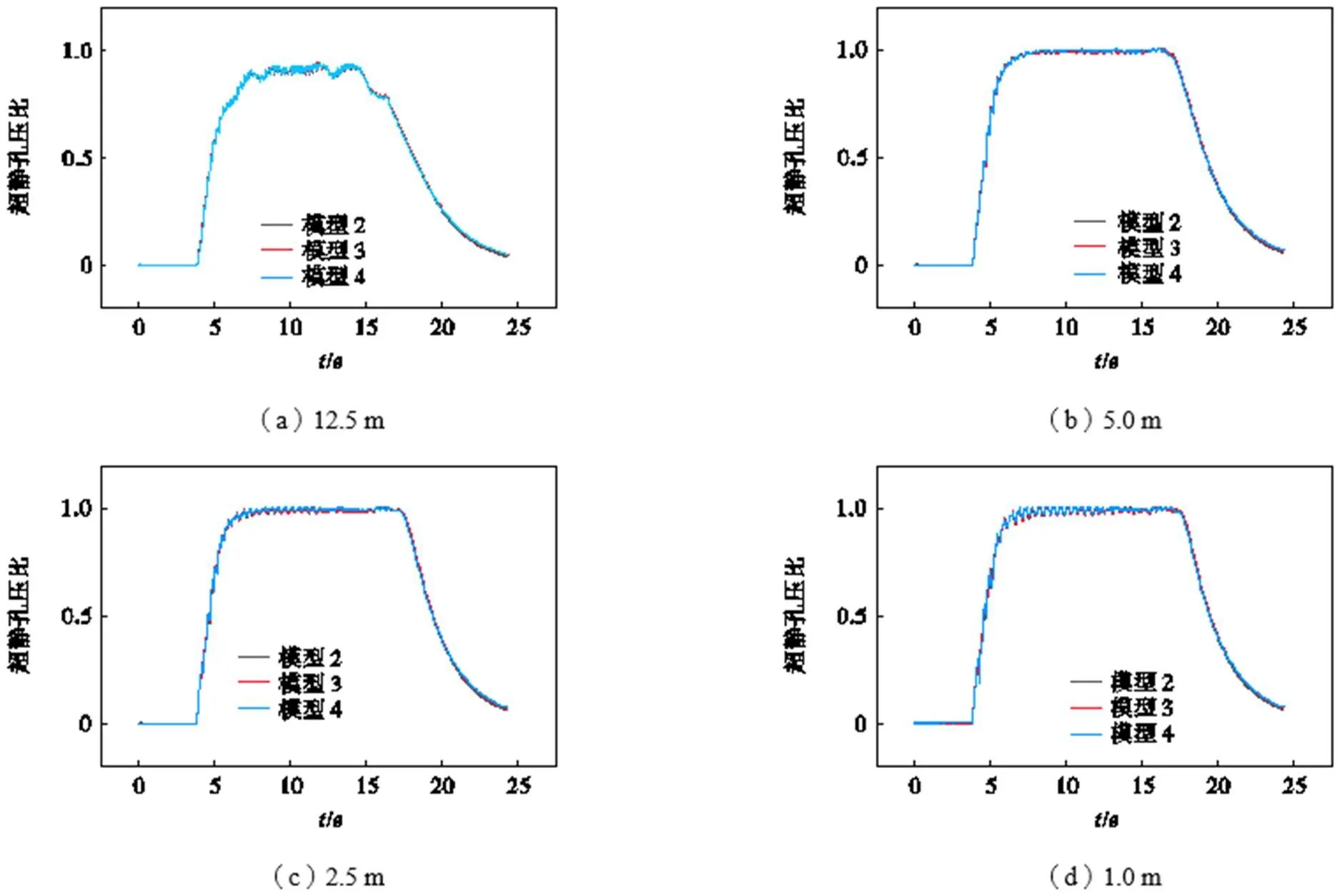
图9 自由场不同深度孔压比时程曲线

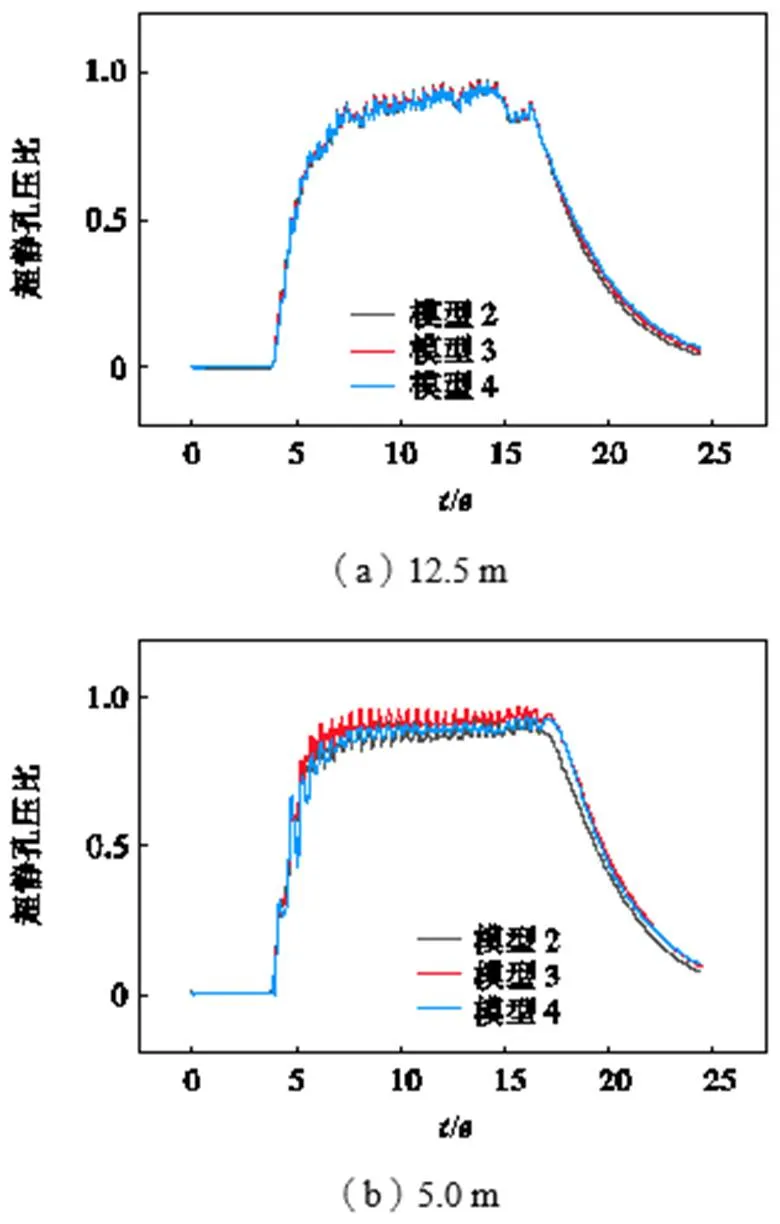
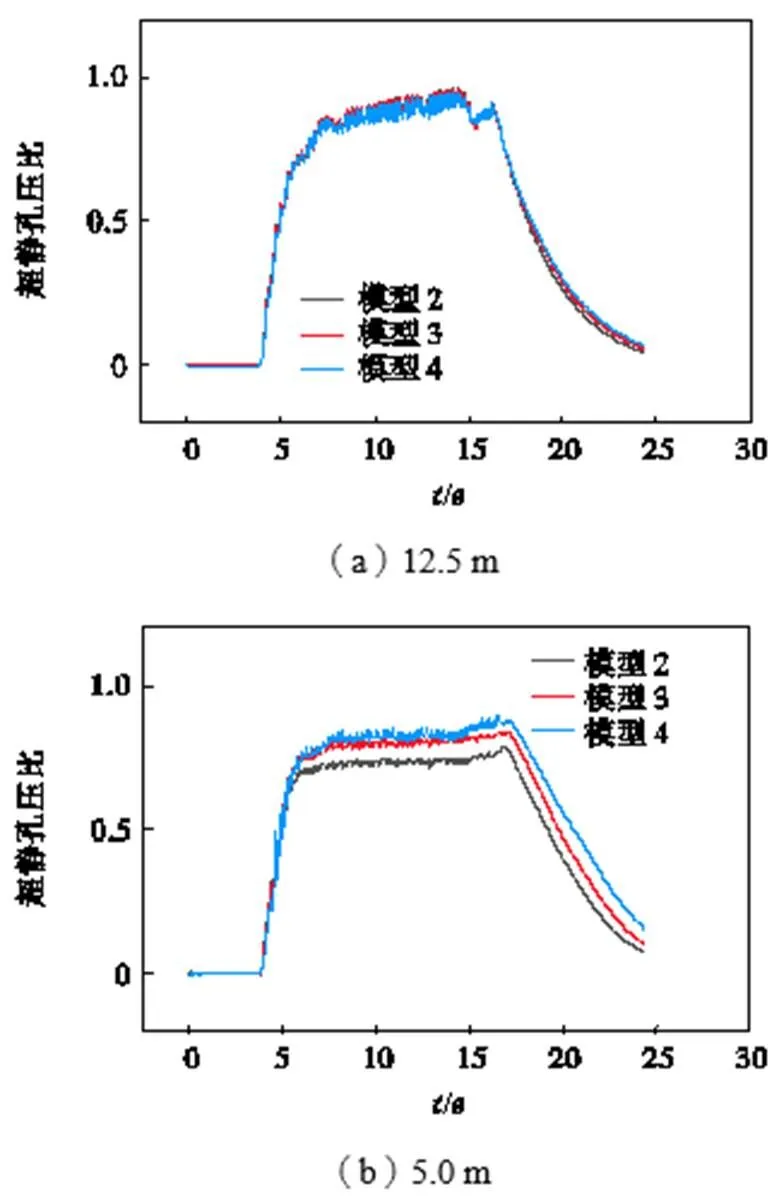
比较3种模型，发现模型2对提高地基的液化性能高于其他两种模型，说明在不增加风机上部载荷的情况下，增大高径比会降低地基抵抗液化的性能．由于桩侧土体作用和附加应力的影响在筒周也发现类似的规律，但其受影响程度小于筒下，所以超静孔压比变化特征介于自由场和筒下之间．综上所述，在地震载荷作用下，筒形基础能够有效加强土体的抗液化能力，不同高径比的筒基表现出不同的液化规律．增大高径比会减弱土体的抗液化能力，但是总的来说，3种模型相同位置处的超静孔压比时程差别较小，对比刘润等[14]的试验结果发现高径比对土体液化的影响不如自重那么明显．

4 结 论

(1) 相对单桩基础，筒形基础的埋深较浅，抗倾覆能力较差，其中矮胖型的筒形基础抗倾覆能力最弱，增大高径比可以有效提升筒基的抗倾覆能力．然而，当高径比超过0.8时提升效果不再明显，对于荷载一定的筒形基础存在一个合适的高径比．

(2) 地震荷载作用下，由于土体弱化发生沉降，筒形基础内的孔压累积上升较大，对相同深度的土体来说，模型筒内部的孔压＞模型筒外部的孔压，模型筒内部孔压的消散速度较慢，筒形基础限制了筒内孔压的消散．

(3) 基于超静孔压比对土体的液化进行了判别，发现自由场和筒基内上部土体发生液化．对于同一深度的土层，筒下土体超静孔压比＜筒周土体超静孔压比＜自由场土体超静孔压比；在受附加应力影响的区域内，随着高径比的增大超静孔压比变大．说明桩土界面的摩擦力和筒基底部的附加应力可以提高土体的抗液化能力，高径比的增大会减弱土体的抗液化能力．

(4) 在随深度增加的方向上，自由场土体抗液化能力逐渐增强；筒周土体抗液化能力在前半段有减弱趋势；筒下土体的抗液化能力则在中间阶段出现反弯点．其中反弯点的设计深度可以较大影响筒形基础的抗震性能，这些规律可以为设计施工提供一个思路.

［1］ 李昊璋，刘苹元，王锦鸿，等. 我国风电产业的发展现状分析及未来展望[J]. 机电信息，2020(21)：91-94.

Li Haozhang，Liu Pingyuan，Wang Jinhong，et al. Analysis of the development status quo and future prospects of China’s wind power industry[J]. Mechanical and Electrical Information，2020(21)：91-94(in Chinese).

［2］ Currie Magnus，Saafi Mohamed，Tachtatzis Christos，et al. Structural integrity monitoring of onshore wind turbine concrete foundations[J]. Renewable Energy，2015，83：1131-1138.

［3］ Berndt M L. Influence of concrete mix design on CO2emissions for large wind turbine foundations[J]. Renewable Energy，2015，83：608-614.

［4］ 舟 丹. 我国海上风电发展目标[J]. 中外能源，2019，24(11)：90.

Zhou Dan. China’s offshore wind power development goals[J]. Sino-Global Energy，2019，24(11)：90(in Chinese).

［5］ Ding Hongyan，Hu Ruiqi，Zhang Puyang，et al. Load bearing behaviors of composite bucket foundations for offshore wind turbines on layered soil under combined loading[J]. Ocean Engineering，2020，198(3)：106997.

［6］ 陈育民，高 星，刘汉龙. 砂土液化流动变形的简化方法[J]. 岩土力学，2013，34(6)：1567-1573.

Chen Yumin，Gao Xing，Liu Hanlong. Simplified method of flow deformation induced by liquefied sand[J]. Rock and Soil Mechanics，2013，34(6)：1567-1573(in Chinese).

［7］ Yu Hao，Zeng Xiangwu，Li Bo，et al. Centrifuge modeling of offshore wind foundations under earthquake loading[J]. Soil Dynamics and Earthquake Engineer-ing，2015，77：402-415.

［8］ Wang Xuefei，Zeng Xiangwu，Yang Xu，et al. Seismic response of offshore wind turbine with hybrid monopile foundation based on centrifuge modelling[J]. Applied Energy，2019，235：1335-1350.

［9］ Wang Xuefei，Zeng Xiangwu，Li Xinyao，et al. Liquefaction characteristics of offshore wind turbine with hybrid monopile foundation via centrifuge modelling[J]. Renewable Energy，2020，145：2358-2372.

［10］ Wang X，Zeng X，Yu H，et al. Centrifuge modeling of offshore wind turbine with bucket foundation under earthquake loading[C]// Proceedings of the International Foundations Congress and Equipment Expo 2015. San Antonio，USA，2015：1741-1750.

［11］ Wang Xuefei，Yang Xu，Zeng Xiangwu. Seismic centrifuge modelling of suction bucket foundation for offshore wind turbine[J]. Renewable Energy，2017，114：1013-1022.

［12］ 刘国威. 筒型基础近海风电系统地震动力响应分析[D]. 天津：天津大学，2012.

Liu Guowei. Seismic Response Analysis of Offshore Bucket Foundation Wind Turbine system[D]. Tianjin：Tianjin University，2012(in Chinese).

［13］ 杨春宝，张建民，王 睿. 海上风电吸力桶基础地震分析[J]. 清华大学学报：自然科学版，2017，57(11)：1207-1211.

Yang Chunbao，Zhang Jianmin，Wang Rui. Seismic analysis of a suction caisson foundation fo offshore wind turbines[J]. Tsinghua Science and Technology：Natural Science，2017，57(11)：1207-1211(in Chinese).

［14］ 刘 润，李成凤，练继建，等. 筒型基础-砂土地基动力响应的离心振动台试验研究[J]. 岩土工程学报，2020，42(5)：817-826.

Liu Run，Li Chengfeng，Lian Jijian，et al. Centrifugal shaking table tests on dynamic response of bucket foundation-sandy soil[J]. Chinese Journal of Geotechnical Engineering，2020，42(5)：817-826(in Chinese).

［15］ 于通顺，王海军. 循环荷载下复合筒型基础地基孔隙水压力变化及液化分析[J]. 岩土力学，2014，35(3)：820-826.

Yu Tongshun，Wang Haijun. Pore water pressure fluctuation and liquefaction analysis of subgrade for composite bucket foundation under cyclic loading[J]. Rock and Soil Mechanics，2014，35(3)：820-826(in Chinese).

［16］ De Risi R，Bhattacharya S，Goda K. Seismic performance assessment of monopile-supported offshore wind turbines using unscaled natural earthquake records[J]. Soil Dynamics and Earthquake Engineering，2018，109：154-172.

［17］ Ueda K，Uzuoka R，Iai S，et al. Centrifuge model tests and effective stress analyses of offshore wind turbine systems with a suction bucket foundation subject to seismic load[J]. Soils and Foundations，2020，60(6)：1546-1569.

［18］ Zhang Puyang，Guo Yaohua，Liu Yonggang，et al. Experimental study on installation of hybrid bucket foundations for offshore wind turbines in silty clay[J]. Ocean Engineering，2016，114：87-100.

［19］ Dashti S，Bray J D，Pestana J M，et al. Mechanisms of seismically induced settlement of buildings with shallow foundations on liquefiable soil[J]. Journal of Geotechnical and Geoenvironmental Engineering，2009，136：151-164.

［20］ 朱 斌，应盼盼，郭俊科，等. 海上风电机组吸力式桶形基础承载力分析与设计[J]. 岩土工程学报，2013，35(增1)：443-450.

Zhu Bin，Ying Panpan，Guo Junke，et al. Analysis and design of bearing capacity of suction caisson foundations of offshore wind turbines[J]. Chinese Journal of Geotechnical Engineering，2013，35(Suppl1)：443-450(in Chinese).

Experimental and Simulation Study on Dynamic Response of a Bucket-Foundation Site for Offshore Wind Turbines

Wang Xuefei1, 2，Ma Chengliang1, 2，Li Jiale1, 2

(1. School of Civil and Transportation Engineering，Hebei University of Technology，Tianjin 300401，China；2. Tianjin Key Laboratory of Prefabricated Building and Intelligent Construction，Tianjin 300401，China)

Bucket foundation is a new type of foundation for offshore wind turbines，and it has the advantages of easy installation，reusability，and low cost. Soil may liquefy under seismic loads，causing a reduction in the soil strength and stiffness，and consequently，a decline in the foundation bearing capacity. A bucket foundation tends to undergo excessive vertical settlement and differential settlement，which severely threatens wind turbine safety. In this study，a series of centrifuge tests were conducted to investigate the seismic response of bucket foundation by recording the time histories of acceleration, pore water pressure, and settlement of surrounding sandy soil. Moreover，numerical analysis was conducted using OpenSees to analyze the dynamic properties of soil，such as stress，strain，and pore pressure. The reliability of the numerical model was verified by the centrifuge test results. The liquefaction characteristics of the bucket foundation were illustrated by considering the soil-foundation interaction，and the influence of aspect ratio was demonstrated. The results showed that the soil under and around the bucket had better resistance to liquefaction owing to the additional stress provided by the foundation. Owing to the long drainage path of the soil inside the bucket foundation，the pore-water pressure dissipates more slowly compared with the soil outside the bucket at the same depth. Moreover，the liquefaction resistance decreased with an increase in the aspect ratio of the bucket. The excess pore-pressure ratio under the bucket reached a minimal value near the bottom of the bucket foundation along the embedment depth. The study results can serve as a design basis for bucket foundation in seismic areas.

bucket foundation；centrifuge test；excess pore-pressure ratio；additional stress；earthquake

TU475+.1

A

0493-2137(2021)08-0790-09

10.11784/tdxbz202010004

2020-10-06；

2021-01-14.

王雪菲（1989—  ），女，博士，副教授，xuefei.wang@hebut.edu.cn.

李家乐，jiale.li@hebut.edu.cn.

国家自然科学基金资助项目(51909054)；河北省自然科学基金资助项目(E2019202056).

Supported by the National Natural Science Foundation of China(No.51909054)，the Natural Science Foundation of Hebei Province (No.E2019202056).

(责任编辑：樊素英)