宽频惯性基准谐振抑制陷波器参数优化方法

李醒飞，郑安琪，拓卫晓，周 政

宽频惯性基准谐振抑制陷波器参数优化方法

李醒飞，郑安琪，拓卫晓，周 政

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

宽频惯性基准(H-IRU)能够提供一束稳定于惯性空间的参考光束，作为捕获、跟踪与瞄准(ATP)系统视轴的惯性参考．根据H-IRU的弹簧-质量模型推导了系统的传递函数，并对系统的频响特性进行了辨识实验．为了抑制H-IRU柔性支撑结构引入的低频谐振，提出了一种改进型陷波器．为了避免因陷波器参数设计不合理导致谐振抑制效果不理想或设计过程反复等情况的发生，提出了一种陷波器参数优化设计方法．以H-IRU系统模型幅频特性曲线最大幅值处的频率确定陷波中心频率，根据系统的直流增益与最大幅值之差确定陷波深度参数，以最小化加入陷波器后系统幅频曲线凸起为目标构造目标函数，对陷波器宽度参数进行快速寻优．将设计的陷波器串联入控制回路，结合不完全微分PID控制和噪声抑制扰动观测器设计了一种混合控制器作为H-IRU的位置环控制器．对串联陷波器后的H-IRU系统的开环及闭环频域特性进行了Matlab仿真，并利用扫频法和辨识法对其实验频域特性进行了测试．仿真和实验结果表明：采用参数优化方法设计的陷波器能够有效抑制系统27Hz附近的低频机械谐振，结合闭环控制方法，可拓展系统闭环带宽至110Hz．

宽频惯性基准；谐振抑制；陷波器；参数优化

H-IRU作为视轴稳定系统的重要组件，能够为ATP系统提供稳定于惯性空间的参考光束[1-3]．为了抑制对地观测、深空探测、激光通信[4-7]等领域存在的角扰动，提高获取图像的分辨率及通信链路信噪比，H-IRU的稳定精度需优于亚微弧度[8]，闭环带宽需要达到100Hz．框架式结构转动惯量较大，且存在轴系摩擦，难以实现对百赫兹带宽内角扰动的有效抑制．由于柔性铰链具有分辨率高、无摩擦、无间隙等优点，本课题[9]采用二自由度圆柱型铰链作为H-IRU系统的支撑结构．为了降低对驱动器输出力的要求，支撑结构一般被设计为：在工作方向上具有较小刚度，而在非工作方向上具有较大的刚度．然而，这种设计会使系统在工作频段内存在1～2个谐振点[10].带宽内谐振的存在会影响系统工作带宽及动态性能，故需要对系统带宽内的谐振进行抑制．

谐振抑制方法主要分为两类．第1类是通过优化结构提高谐振频率或减小谐振幅度，如改进结构材料和加工工艺、配置减震器等[11]．第2类是通过控制方法或增加补偿器的手段抑制谐振．对于系统结构已经设计加工完成的系统，第1类方法实施困难，制造成本较高[12]．因此，大多数文献采用的是第2类谐振抑制方法，其可分为主动抑制和被动抑制.

主动抑制方法是指通过改变系统控制结构或参数实现谐振抑制．关于主动谐振抑制的方法，学者已经进行了诸多研究，主要包括：①基于PI/PID控制的谐振抑制[13-14]；②基于观测器的谐振抑制[15-16]；③基于先进控制算法的谐振抑制[17-18]．然而，主动抑制方法设计过程一般较为复杂．另外，一些先进算法计算量大，在工程实现中受硬件计算速度限制，难以广泛使用．

被动抑制方法一般通过在系统中加入补偿器实现谐振抑制，常用的补偿装置为陷波滤波器[19]．采用陷波器补偿谐振原理简单，不需要增加其他硬件，且易于实现，因此得到广泛应用．王建敏等[20]结合陷波器和二阶低通滤波器的特点设计了一种双二次型滤波器，实现对转台伺服系统中谐振点和反谐振点的同时抑制．张士涛等[21]针对双二次型陷波器无法单独调节谐振点和反谐振点处峰值的问题，提出了一种由两个双Ｔ型陷波器和一个低通滤波器组成的新型结构滤波器，并将其成功应用到航空光电稳定平台系统的谐振抑制中．王昱忠等[22]采用改进双T型陷波器弥补传统陷波器无法调整陷波深度的问题，结合改进FFT算法实现谐振的在线检测和抑制．

上述文献中陷波器参数设计多依赖于设计人员的工程经验．为了缩短设计周期并提高设计可靠性，诸多学者对陷波器的参数整定方法进行了研究. Teng等[23]在超精密运动控制中，以最小化定位误差为设计目标，提出了一种迭代调谐算法对陷波器参数进行了整定．这种方法不需要建立准确系统模型，且能够弥补经验法取值效果不理想的问题．李文涛等[24]基于改进粒子群算法提出了一种陷波器参数优化设计方法，通过对速度偏差信号进行FFT变换实现机械谐振在线分析与补偿．然而，基于FFT的陷波器参数在线优化方法实时性较差，无法应用于H-IRU系统的谐振抑制．

本文采用改进双T型陷波器实现对H-IRU系统低频机械谐振的抑制．以对系统幅频特性曲线凸起的抑制程度作为谐振抑制效果的评价标准．根据这一标准构造目标函数，在对目标函数寻优的过程中确定陷波器参数．对所设计陷波器进行了仿真及实验验证，并将所设计的陷波器加入闭环控制回路进行了闭环实验．

1 H-IRU系统原理及模型分析

1.1 系统工作原理

H-IRU系统工作原理如图1所示，采用柔性支撑结构为系统提供、两个方向上的转动自由度，通过4个音圈电机两两推挽驱动实现平台的小角度转动.当H-IRU系统受到角扰动时，磁流体动力学(magnetohydrodynamic，MHD)角速度传感器[25]和MEMS陀螺仪将敏感到的角振动信息反馈至控制器，控制器输出控制信号至电机驱动器，控制音圈电机反方向推动台面，使台面相对于惯性空间保持稳定．另外，H-IRU也可实现精确指向，当有外部指令输入时，电涡流位移传感器将敏感到的角度信息反馈到位置环控制器，控制台面偏转指定角度．由于系统、轴两个工作方向互相解耦且结构对称，故本文以对轴为例进行分析．

1.2 系统模型分析

根据H-IRU工作原理和基本结构[26]，建立其弹簧-质量模型如图2所示．

系统力矩平衡方程为

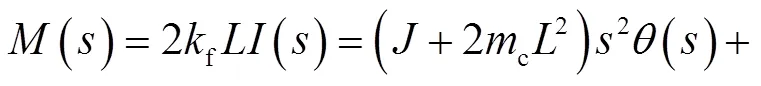
电压平衡方程为

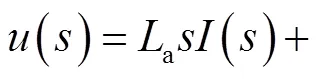
联合力矩平衡方程和电压平衡方程得到H-IRU传递特性为

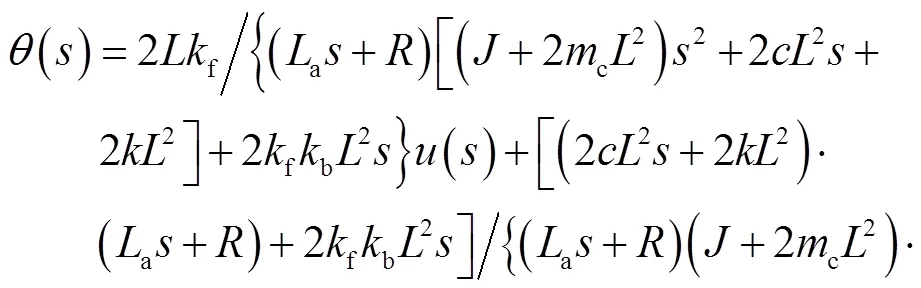
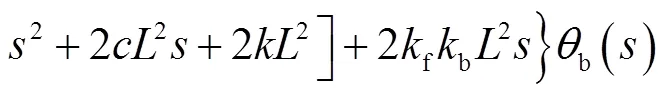
式(3)中第1项为H-IRU系统从输入电压到输出角度的传递特性，即系统被控对象特性．该项传递特性可分解为一个惯性环节和一个二阶振荡环节的串联，即

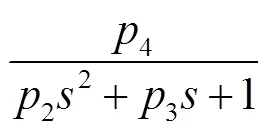
式(4)中二阶振荡环节的存在会引入系统低频谐振．

由于存在加工及装配误差，理论分析无法获得系统真实模型．为了便于陷波器的优化设计，本文采用Levy法对系统模型进行辨识．实验中采用0.1～600Hz、间隔为0.1Hz的多正弦混频信号作为激励信号，在3个电压幅值(0.8V，1.0V，1.2V)下，对系统从输入电压(V)到输出角度(rad)的传递函数进行了辨识．9组辨识实验得到的传递函数拟合度均超过0.99．选取其中拟合度最高的一组辨识结果为

如图3所示．可见系统在166.856rad/s频率处存在一个峰值为29.3dB的低频谐振．

由图3可见，系统低阶谐振频率较低(约27Hz)，位于工作带宽(110Hz)内，且系统阻尼系数较小，谐振峰值较大(29.3dB)．因此在进行闭环控制设计时，为保证系统稳定，要求闭环控制器增益不能太大，从而导致闭环带宽无法大幅提升．因此本文将陷波器串联入控制回路，以在抑制谐振的同时构造一个具有良好开环特性的被控对象模型，使得控制器增益不再受限，在保证系统稳定性的同时提高系统带宽.

图3 辨识实验结果

2 双T型陷波器优化设计

2.1 双T型陷波器原理

双T型陷波器传递函数[19]为

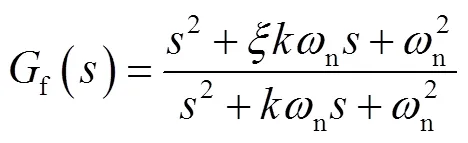
式中：为陷波器深度参数；为陷波器宽度参数；为陷波中心频率．陷波器的设计步骤一般为：先确定陷波中心频率，之后通过调整滤波器的、两个参数实现谐振的抑制．不同的、参数对应的陷波器特性如图4和图5所示．

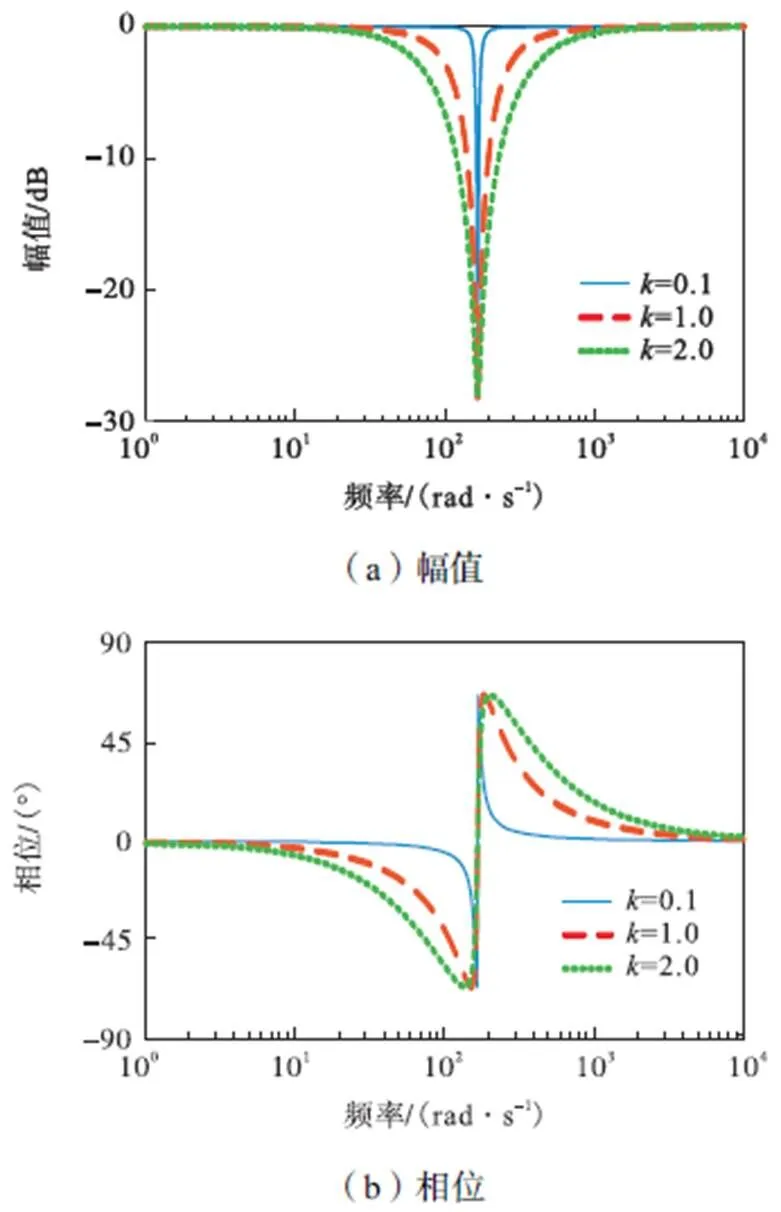
图5 宽度参数对陷波器影响()

2.2 优化设计策略

为了便于双T型陷波器参数的频域整定，本文将陷波频率、陷波幅值、陷波宽度直接作为陷波器的设计参数．所使用的陷波器传递函数为

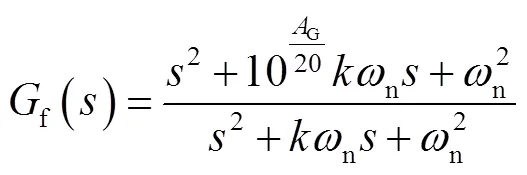
式中为陷波器中心频率对应的陷波深度，其幅频特性示意如图6(a)所示．图6(b)给出了存在谐振系统、陷波器和串联陷波器后系统的幅频曲线示意．其中代表系统直流增益，、为幅值高于直流增益对应的临界频率点，为谐振中心频率.由图6(b)可见：系统在频段内曲线存在明显凸起，在频率处发生谐振，谐振最大峰值为．

要得到最优谐振抑制效果，需要保证

根据上述优化思想，确定如下设计步骤．

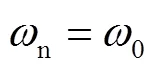
2.3 双T型陷波器优化设计结果

图7 Matlab仿真结果

图7(b)、(c)为串联陷波器前后系统开环特性曲线仿真，串联陷波器后，谐振明显得到抑制．

将陷波器参数代入式(7)，得到陷波器传递函数为

3 实验验证与结果分析

根据图8所示的系统硬件测试框图，搭建了实验测试系统，如图9所示．利用上位机产生激励信号并对传感器的输出信号进行预处理．选用NI USB 6255采集卡进行数据采集，并通过串口将数据传输至上位机．利用NI DAQ7845R-FPGA模块将设计的陷波器与控制器实时实现，采用线性电源为实验系统供电．

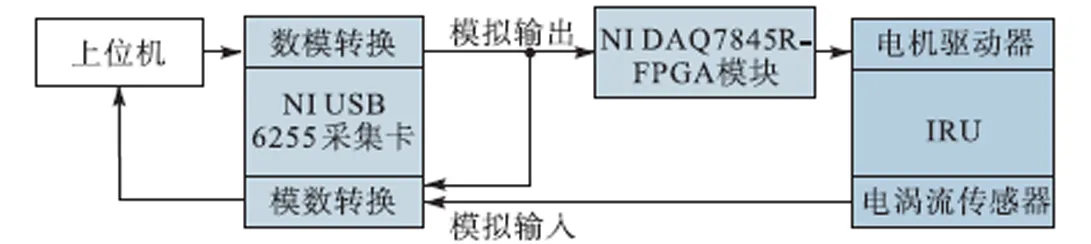
图8 系统硬件测试框图

图9 实验测试系统实物图

3.1 机械谐振抑制实验验证

为验证优化设计的陷波器谐振抑制效果，对加入陷波器后的系统进行辨识实验．9组不同激励信号幅值的辨识结果重复性较好(偏离程度＜0.3%)，且拟合优度均高于0.9．其中，拟合度最高的辨识结果为

为进一步验证模型辨识的精度，对系统的频响特性进行扫频法测试．测试方法为：分段固定激励电压幅值，进行频率范围为1～200Hz，频率间隔为1Hz的扫频测试．具体的激励电压给定方式如下：1～40Hz：0.2V；41～80Hz：0.4V；81～120Hz：0.6V；121～160Hz：0.8V；161～200Hz：1.0V．将扫频测试结果与Levy法辨识结果式(17)进行对比，如图10所示．由图10可见，加入陷波器后谐振得到有效抑制，且系统开环频域特性曲线平坦．

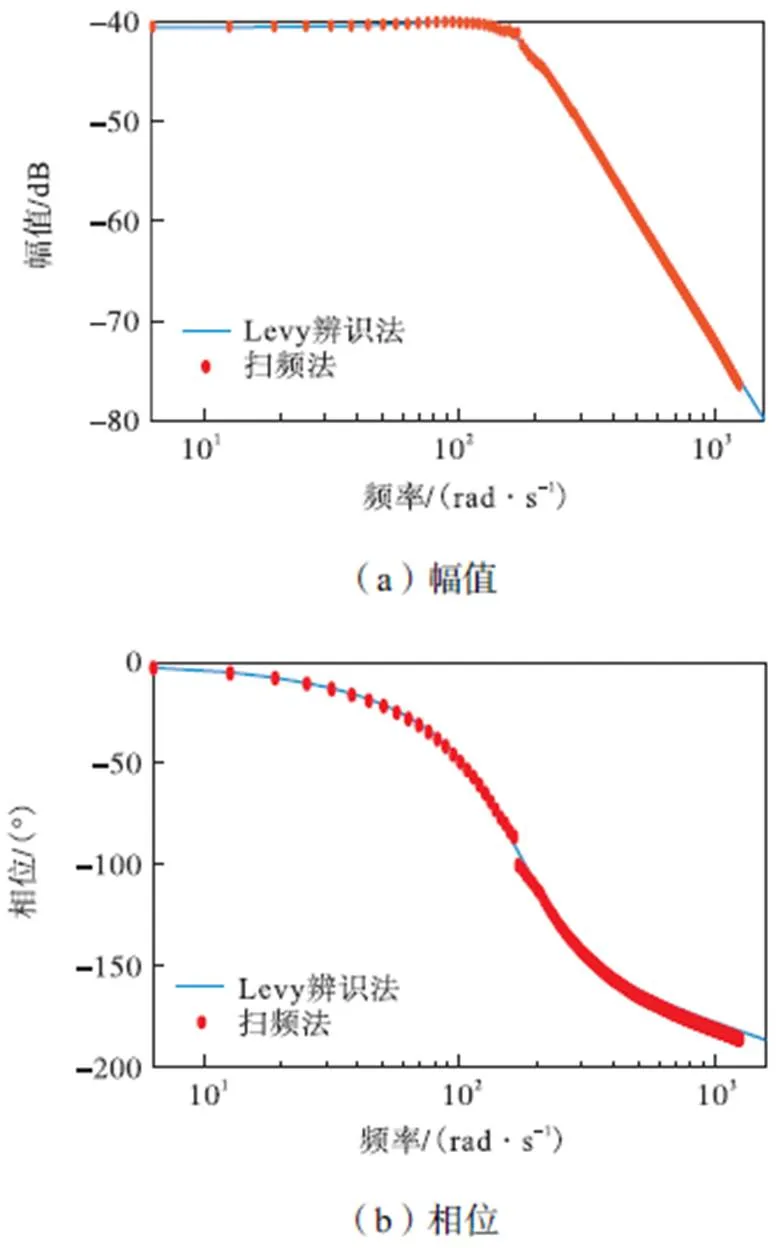
图10 扫频法与辨识法辨识实验结果

绘制辨识模型和扫频法测试结果误差曲线如图11所示．由图11可看出，在1～200Hz频带范围内，Levy法辨识结果精度较高，幅值及相位拟合误差均较小，幅值误差小于±0.7dB，相位误差小于±7°．上述结果表明，Levy法辨识模型能够反映系统实际模型，辨识模型的结果可以作为控制器设计依据．

3.2 闭环实验

为了进一步验证引入陷波器后系统的闭环动态特性，本文设计了不完全微分PID结合噪声抑制扰动观测器(DOB)的混合控制结构，用于验证惯性基准系统的位置闭环特性．加入DOB的目的在于抑制高频噪声，提高系统稳定性．谐振抑制效果的好坏将影响控制器的设计，在谐振频率附近，若系统名义模型与系统实际模型偏差较大，将导致对扰动的观测不准确，影响系统稳定性．

图11 Levy辨识法结果误差分布

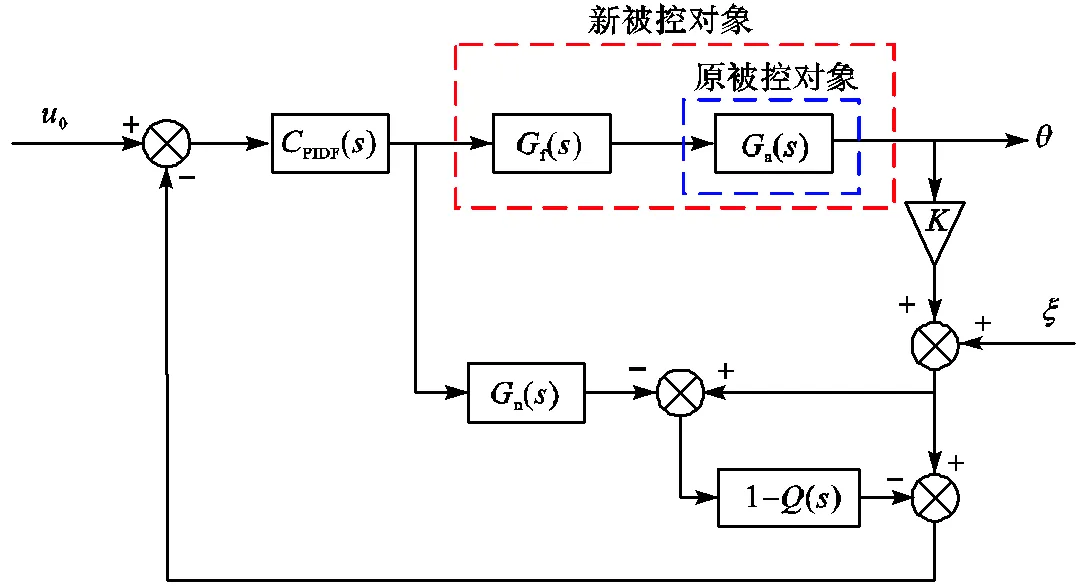
图12 闭环控制结构

对基于不完全微分PID和DOB复合控制器的闭环系统进行扫频测试．将扫频结果、闭环控制器设计仿真结果及开环模型的对比曲线绘制如图13和图14所示．图13为未加陷波器的原系统开环模型及其闭环频域特性曲线，图14为加入陷波器构成的新被控对象开环及闭环模型频域特性曲线．由图13和图14可见，闭环系统扫频测试结果与仿真相符，验证了闭环控制方案．由图13可见，未加陷波器系统仅靠反馈控制无法完整抑制谐振峰，闭环带宽很低，仅为7.96Hz．由图14可见，加入陷波器后系统闭环带宽可达到110Hz．与未加陷波器系统相比，带宽得到了极大的扩展．

图13 未加陷波器闭环系统频域特性曲线

图14 加入陷波器闭环系统频域特性曲线

综上实验结果，本文所设计陷波器有效抑制机械谐振，改善了系统开环传递特性，保证DOB中名义模型符合实际模型情况，测量噪声抑制能力得到提高，显著拓展了系统闭环带宽．

4 结 语

为抑制宽频惯性基准柔性支撑引入的低频谐振，提高系统的带宽和动态性能，本文采用改进双T型陷波器对系统谐振进行抑制．为了克服陷波器参数整定多依赖于工程经验的问题，提出了一种参数优化设计方法，并完成了优化陷波器的设计与仿真．对加入陷波器后的系统进行了点频法测试和模型辨识，结果表明：模型辨识精度较高(幅值误差小于±0.7dB，相位误差小于±7°)．根据辨识模型，设计了不完全微分PID-DOB复合控制器对惯性基准位置环的带宽特性进行了测试．闭环实验结果证明，系统闭环带宽达到110Hz，远大于系统低阶谐振频率(27Hz)及未串联陷波器系统闭环带宽(7.96Hz)．

［1］ Hilkert J M. Inertially stabilized platform technology Concepts and principles[J]. IEEE Control Systems Magazine，2008，28(1)：26-46.

［2］ 马佳光. 捕获跟踪与瞄准系统的基本技术问题[J]. 光学工程，1989，16(3)：1-42.

Ma Jiaguang. The basic technologies of the acquisition，tracking and pointing system[J]. Opto-Electronic Engineering，1989，16(3)：1-42(in Chinese).

［3］ 田 竞，邓 超，曹 政，等. 加速度反馈技术在惯性稳定平台中的应用[J]. 光电工程，2016，43(12)：40-45.

Tian Jing，Deng Chao，Cao Zheng，et al. Application of acceleration feedback techniques on inertial stabilization platform[J]. Opto-Electronic Engineering，2016，43(12)：40-45(in Chinese).

［4］ 胡浩军. 运动平台捕获、跟踪与瞄准系统视轴稳定技术研究[D]. 长沙：国防科学技术大学，2005.

Hu Haojun. Line-of-Sight Stabilization of Acquistion，Tracking and Pointing System on Moving Bed[D]. Changsha：National University of Defense Technol-ogy，2005 (in Chinese).

［5］ Toyoshima M，Takayama Y，Kunimori H，et al. In-orbit measurements of spacecraft microvibrations for satellite laser communication links[J]. Optical Engineer-ing，2010，49(8)：578-578.

［6］ Jono T，Takayama Y，Sodnik Z，et al. OICETS on-orbit laser communication experiments[J]. Proc SPIE，2006，6105：13-23.

［7］ Burnside J W，Murphy D V，Knight F K，et al. A hybrid stabilization approach for deep-space optical communications terminals[J]. Proceedings of the IEEE，2007，95(10)：2070-2081.

［8］ Downey G，Stockum I D L. Electro-optical tracking systems considerations[J]. Proceedings of SPIE-The International Society for Optical Engineering，1989，1111：70-84.

［9］ 胡亚婷. 基于MHD的宽频惯性稳定平台柔性支撑结构设计方法研究[D]. 天津：天津大学，2018.

Hu Yating. Study on the Design Method of Flexure Support Structure for Board Band Intertial Reference Stabilization Platform Based on MHD[D]. Tianjin：Tianjin University，2018(in Chinese).

［10］ 徐 宁. 基于柔性机构的快速反射镜研究[D]. 吉林：中国科学院长春光学精密机械与物理研究所，2018.

Xu Ning. Research on Fast Steering Mirror Based on Compliant Mechanism[D]. Jilin：Changchun Institute of Optics，Fine Mechanics and Physics Chinese Academy of Sciences，2018(in Chinese).

［11］ 郭高洁. 伺服控制系统谐振实时抑制方法探究[D]. 成都：中国科学院光电技术研究所，2018.

Guo Gaojie. Online Resonance Suppression Exploration of Servo system[D]. Chengdu：The Institute of Optics and Electronics，Chinese Academy of Science，2018(in Chinese).

［12］ 熊 琰. 伺服驱动系统机械谐振问题研究[D]. 武汉：华中科技大学，2015.

Xiong Yan. Research on Mechanical Resonance in Servo Drive System[D]. Wuhan：Huazhong University of Science & Technology，2015(in Chinese).

［13］ 王 璨，杨 明，徐殿国. 基于PI控制的双惯量弹性系统机械谐振的抑制[J]. 电气传动，2015，45(1)：49-53.

Wang Can，Yang Ming，Xu Dianguo. Mechanical resonance suppression of the elastic two-inertia system based on PI control[J]. Electric Drive，2015，45(1)：49-53(in Chinese).

［14］ 唐 涛，黄永梅，张 桐，等. 负载加速度反馈的伺服系统谐振抑制[J]. 光电工程，2007，34(7)：14-17.

Tang Tao，Huang Yongmei，Zhang Tong，et al. Reduction of mechanical resonance based on load acceleration feedback for servo system[J]. Opto-Electronic Engineering，2007，34(7)：14-17(in Chinese).

［15］ 李文涛，白瑞林，朱渊渤. 基于双观测器的伺服系统谐振抑制方法[J]. 仪表技术与传感器，2019(4)：95-99.

Li Wentao，Bai Ruilin，Zhu Yuanbo. Servo system resonance suppression method based on double observer [J]. Instrument Technique and Sensor，2019(4)：95-99(in Chinese).

［16］ Bang J S，Shim H，Park S K，et al. Robust tracking and vibration suppression for a two-inertia system by combining backstepping approach with disturbance observer[J]. IEEE Transactions on Industrial Electronics，2010，57(9)：3197-3206.

［17］ Cychowski M，Szabat K，Orlowska-Kowalska T. Constrained model predictive control of the drive system with mechanical elasticity[J]. IEEE Transactions on Industrial Electronics，2009，56(6)：1963-1973.

［18］ Li Xin，Zhou Wenlin，Luo Jun，et al. A new mechanical resonance suppression method for large optical telescope by using nonlinear active disturbance rejection control[J]. IEEE Access，2019(7)：94400-94414.

［19］ 杨 辉，范永坤，舒怀亮. 抑制机械谐振的一种改进的数字滤波器[J]. 光电工程，2004，31(增1)：30-32，39.

Yang Hui，Fan Yongkun，Shu Huailiang. An improved digital filter for restraining mechanical resonance frequency[J]. Opto-Electronic Engineering，2004，31(Suppl 1)：30-32，39(in Chinese).

［20］ 王建敏，吴云洁，刘佑民，等. 基于数字滤波器的伺服系统谐振抑制方法[J]. 北京航空航天大学学报，2015，41(3)：485-491.

Wang Jianmin，Wu Yunjie，Liu Youmin，et al. Resonance suppression method based on digital filter for servo system[J]. Journal of Beijing University of Aeronautics and Astronautics，2015，41(3)：485-491(in Chinese).

［21］ 张士涛，张 葆，李贤涛，等. 基于结构滤波器的伺服系统谐振抑制[J]. 光学精密工程，2019，27(8)：1811-1818.

Zhang Shitao，Zhang Bao，Li Xiantao，et al. A method of servo system resonance suppression based on structure filter[J]. Optics and Precision Engineering，2019，27(8)：1811-1818(in Chinese).

［22］ 王昱忠，何 平，王志成，等. 基于自适应陷波器的伺服系统谐振抑制[J]. 组合机床与自动化加工技术，2019(1)：68-71.

Wang Yuzhong，He Ping，Wang Zhicheng，et al. Servo system resonance suppression based on adaptive notch filter[J]. Modular Machine Tool ＆ Automatic Manufacturing Technique，2019(1)：68-71(in Chinese).

［23］ Teng Wei，Yang Liangliang，Zhang Yangyang，et al. Iterative tuning notch filter for suppressing resonance in ultra-precision motion control[J]. Advances in Mechanical Engineering，2016，8(11)：1-9.

［24］ 李文涛，白瑞林，朱渊渤. 陷波滤波器谐振抑制参数优化方法[J]. 噪声与振动控制，2018，38(3)：20-25.

Li Wentao，Bai Ruilin，Zhu Yuanbo. Optimization method of resonant suppression parameters of notch filters[J]. Noise and Vibration Control，2018，38(3)：20-25(in Chinese).

［25］ 李醒飞，周新力，吴腾飞，等. 一种MHD角速度传感器与MEMS陀螺仪组合测量系统信号融合的方法[J]. 天津大学学报：自然科学与工程技术版，2018，51(2)：159-166.

Li Xingfei，Zhou Xinli，Wu Tengfei，et al. A method of signal fusion for combination measurement system of MHD angular rate sensor and MEMS gyro[J]. Journal of Tianjin University：Science and Technology，2018，51(2)：159-166(in Chinese).

［26］ Li Dong，Wu Tengfei，Ji Yue，et al. Model analysis and resonance suppression of wide-bandwidth inertial reference system[J]. Nanotechnology and Precision Engineering，2019，2(4)：177-187.

Optimization Method of Notch Filter Parameters in Resonant Suppression of High-Bandwidth Inertial Reference Unit

Li Xingfei，Zheng Anqi，Tuo Weixiao，Zhou Zheng

(State Key Laboratory of Precision Measurement Technology and Instruments，Tianjin University，Tianjin 300072，China)

The high-bandwidth inertial reference unit(H-IRU)provides a reference beam stabilized in the inertial space as the inertial reference of the line-of-sight of acquisition，tracking，and pointing system. According to the spring-mass model of the H-IRU system，the transfer function of the system was derived，and the frequency characteristics were identified and experimentally tested. To suppress the low-frequency resonance induced by the flexible support structure of inertial reference and to avoid undesirable resonance suppression effect，an improved notch filter with a parameter optimization design is proposed. The notch frequency is determined by the frequency at the maximum amplitude of the system amplitude frequency curve while the depth parameter is obtained from the difference between the DC gain and the maximum amplitude of the system. An objective function is constructed to minimize the amplitude frequency curve bulge after the addition of the notch filter which quickly optimizes the notch width parameter. The notch filter was connected in series to the control loop. A hybrid controller was designed as the position loop controller of H-IRU by combining the incomplete differential PID control and the noise suppression disturbance observer. The open-loop and closed-loop frequency domain characteristics of H-IRU system after series notch filter were observed through Matlab simulations while the experimental frequency domain characteristics were tested using frequency sweep and identification methods. Simulation and experimental results reveal that the proposed notch filter designed by the parameter optimization method effectively suppresses the low-frequency mechanical resonance near 27Hz. Combined with the closed-loop control method，the closed-loop bandwidth of the system can be extended to 110Hz.

high-bandwidth inertial reference unit(H-IRU)；resonance suppression；notch filter；parameters optimization

V19

A

0493-2137(2021)08-0852-09

10.11784/tdxbz202009007

2020-09-02；

2020-10-15.

李醒飞（1966—  ），男，博士，教授.

李醒飞，lixf@tju.edu.cn.

国家自然科学基金重点资助项目(61733012).

Supported by the Key Program of the National Natural Science Foundation of China(No. 61733012).

(责任编辑：孙立华)