基于改进CEEMDAN分解的GNSS-RTK监测信号处理方法

于丽娜，熊春宝，熊爱成，朱劲松，王 猛

基于改进CEEMDAN分解的GNSS-RTK监测信号处理方法

于丽娜1，熊春宝1，熊爱成2，朱劲松1，王 猛1

(1. 天津大学建筑工程学院，天津 300072；2. 天津市陆海测绘有限公司，天津 300191)

GNSS-RTK监测精度受多路径效应和仪器内部白噪声的影响，为此，提出基于有效系数筛分本征模式函数(IMF)分量的改进CEEMDAN算法分离信号和噪声，以提升GNSS-RTK监测精度．首先，通过仿真信号验证该算法的白噪声分离效果．然后，进行GNSS-RTK连续多天定点观测试验，验证采用改进CEEMDAN算法提取多路径误差的可行性．接着，在开阔的平坦地面和水面分别进行GNSS-RTK稳定性试验，分析不同环境下的多路径效应．最后，以天津海河大桥为对象，对GNSS-RTK监测信号进行滤波降噪，进而提取桥梁在环境激励下的动力响应．结果表明：改进CEEMDAN算法能够实现更精确的IMF分量分解与重构，从而有效分离高频白噪声分量和低频多路径误差；在开阔的平坦地面和水面环境下多路径效应影响均较小，多路径误差序列频域分布为地面(0.05Hz)＜水面(0.10Hz)．结合结构自振频率及现场环境确定带通滤波频带，对GNSS-RTK实测信号进行滤波降噪处理，成功提取了海河大桥的动态位移，结果与拾振器监测结果基本一致．

改进CEEMDAN；GNSS-RTK；连续定点观测试验；稳定性试验；桥梁动态变形监测

全球导航定位技术(global navigation satellite system，GNSS)是包括GPS、GLONASS、Galileo和BDS系统的多星座联合应用技术，具有快速高效、全自动全天候、实时高精度等诸多优势，且具有良好的环境适应性，可用于监测环境激励下结构的动力响应．随着采样频率的提升，GNSS技术被广泛应用于高层建筑、大坝、桥梁等大型土木工程结构变形监测[1-2]．实时动态(real-time kinematic，RTK)载波相位差分技术是一种利用双测站载波相位观测值进行实时动态差分定位的方法，可消除或削弱GNSS监测中的电离层、对流层延迟，卫星、接收机钟差，对卫星星历误差也有很好的抑制作用．然而，由于多路径误差在基线两端不具有相关性，因而无法通过差分方法消除多路径效应影响．通过安装扼流圈天线或组合天线，能够削弱天线下方反射物造成的多路径误差，但对天线周围反射物造成的多路径效应则无能为力[3-5]．由接收机天线周围反射物造成的多路径效应和仪器内部产生的随机噪声成为GNSS-RTK监测的主要噪声来源[6-8]．

在接收机天线固定不变且其周围环境变化很小时，通过连续多天静态监测结果构建误差修正模型进行恒星日滤波，对削弱多路径效应十分有效[5,9]．然而，在实际的工程应用中，连续多天定点静态监测对设备性能要求高，且监测环境的变化会对采集信号造成不确定性干扰．此外，环境激励下结构本身的动力响应导致难以获取静态条件下的变形序列[10]．因此，在实际工程应用中，难以通过恒星日滤波原理修正GNSS-RTK监测的多路径误差．多路径效应与反射物的数量、反射能力以及反射物与接收机的几何关系密切相关[11]．障碍物遮挡、强反射漫反射以及电磁波干扰等都会产生较大的多路径效应[12]，因此，在考虑监测环境不确定性的同时，一些典型环境下GNSS多路径误差的特性值得进一步研究．

研究表明，GNSS-RTK仪器内部产生的随机噪声频域分布范围较宽，有明显的高斯白噪声特性[13].由于结构振动频率可能与仪器噪声频率混叠，故无法基于频域滤波原理消除仪器白噪声干扰．

为了提升GNSS-RTK结构监测精度，学者们对GNSS-RTK信号滤波降噪方法进行了诸多研究．基于经验模态分解(EMD)经典算法及其改进算法的滤波方法得到了广泛应用．戴吾蛟等[5]、罗飞雪等[6]采用EMD方法削弱GPS多路径效应，提出EMD-ICA联合滤波方法．严超等[14]结合EMD和递归最小二乘算法(RLS)的优势，提出了一种EMD-RLS联合滤波算法．针对多路径误差和仪器随机噪声的频谱特性，伊廷华等[15]提出对具有强相关特性的低频多路径误差采用自适应噪声滤波，而对于不相关的高频噪声进行小波分解，最后重构得到真实测量信号．Wang等[16]提出了EMD-Wavelet联合算法提取噪声分量，该方法能够最大限度发挥小波滤波和EMD各自的优势，但仍受其算法本身缺陷的影响．针对EMD算法存在的模态混叠问题，赵龙等[8]提出了完备经验模态分解(CEEMD)与Wavelet-SavGol的联合滤波算法．针对CEEMD算法的附加模态问题，Torres等[17]提出了一种具有自适应噪声的完全集合经验模态分解方法(CEEMDAN)，该方法通过添加自适应白噪声和计算唯一的残余分量，可实现IMF的更精确重构，在机械构件性能检测、雷达信号细微特征分析等均达到了较高的识别精度[18-19]．

本文提出利用CEEMDAN方法对GNSS-RTK信号进行分解，并选择有效系数作为筛分标准筛选及重构IMF分量，从而分离出多路径误差和仪器内部随机噪声．首先，通过仿真信号验证了改进CEEMDAN算法的噪声分离效果；然后，进行了GNSS-RTK连续多天定点观测试验，基于所提算法对观测数据进行处理，并与恒星日滤波结果进行对比分析．接着，在开阔的平坦地面和水面上进行GNSS-RTK稳定性试验，分析了不同监测环境下的多路径效应．最后，以天津海河大桥为对象，联合改进CEEMDAN算法和巴特沃斯高通滤波器对GNSS-RTK信号进行滤波降噪处理，提取桥梁动态位移并与拾振器监测结果进行对比，验证改进CEEMDAN算法应用于GNSS-RTK实测信号的有效性．

1 CEEMDAN改进算法

1.1 CEEMDAN基本原理

EMD是一种经典自适应信号时频处理方法，其原理是根据信号本身特征进行多次分解，从而获取一组本征模式函数(IMF)分量和一个残余分量[20]．IMF分量包含了原信号的不同时间尺度的局部特征信号，须满足如下条件：①在整个时间范围内，IMF分量的局部极值点和过零点的数目必须相等，或最多相差一个；②在任意时刻，上包络线和下包络线的平均必须为零．

CEEMDAN算法的核心是在EMD算法的基础上，通过添加自适应白噪声并且计算唯一残余分量，实现对IMF分量更精确的重构．它很好地避免了EEMD[21]添加白噪声造成的噪声污染问题，以及CEEMD[22]添加不同噪声可能造成IMF分量数目不同的问题，其基本算法如下.

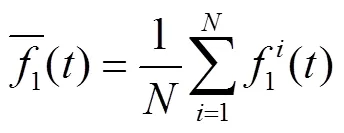
(2) 第1个残余信号为

(6) 循环步骤(4)和(5)，直到分解完成，得到最终的残余分量

1.2 基于有效系数的IMF分量重构

高斯白噪声主导的IMF分量，其能量密度与平均周期的乘积为常量，定义为能量系数．

能量密度的表达式为

平均周期表达式为

能量系数表达式为

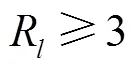
2 仿真信号验证

仿真信号由周期为1200s、600s和300s的正弦信号组成，可表示为

数据取样间隔为1s，样本长度4000．对原仿真信号叠加正态高斯白噪声，构成加噪信号

图1分别给出了原始仿真信号、加噪信号、去噪后信号和分离出的白噪声信号．

为了验证改进CEEMDAN算法的噪声分离效果，以相关系数(CC)作为评价指标对仿真信号进行验证，其表达式为

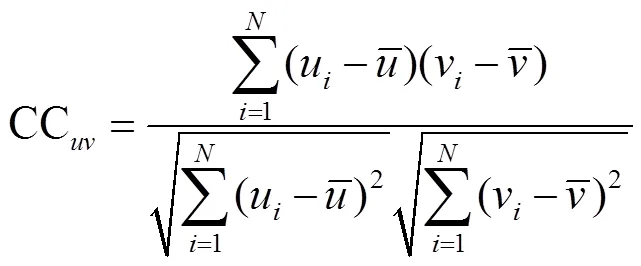
由于原始信号与真实IMF分量的相关性较强，与虚假IMF分量(白噪声)的相关性较弱，因此，可通过阈值来筛分和重构IMF分量，阈值表达式为

图1 仿真信号处理

表1 仿真信号IMF分量有效系数及相关系数

Tab.1 Effective coefficients and correlation coefficients of the simulation signal’s IMFs

3 GNSS-RTK多路径误差分析试验

为了验证改进CEEMDAN算法提取多路径误差的可靠性，在天津市滨海新区陆海测绘公司楼顶进行GNSS-RTK连续多天定点观测试验，如图2所示．试验选用3台海星达H32型GNSS-RTK接收机，1台作基准站，2台作流动站，以相互验证．设备统一调制为GPS/GLONASS/BDS三星座组合系统，卫星高度截止角为15°，数据采样频率为5Hz．接收机位置固定，连续3天采集信号．

图2 GNSS-RTK连续多天定点监测试验

图3为连续3天同一时段、高程方向、时长为28000s的原始位移序列．可以看出，3组序列整体形态相似，具有明显的重复性．分别对3组数据进行CEEMDAN分解，并根据式(7)～(10)计算了有效系数，结果如表2所示．3组序列的IMF1～IMF7的有效系数均小于3，判定为高频噪声分量；IMF8～IMF14判定多路径误差分量．

图3 3天原始位移序列

高频噪声分量和多路径误差分量如图4所示.可以看出，高频噪声分量呈现明显的白噪声特性，3组多路径误差序列具有明显的重复性．选择相关系数和标准差为评价指标量化噪声分离效果．3组多路径误差序列两两间的相关系数分别为CC12＝0.784、CC23＝0.803、CC13＝0.804，显示出较高的相关性．多路径误差修正前后的位移标准差如表3所示．以第1天的多路径误差序列对第2、3天的原始序列进行修正，修正后的位移序列标准差大于高频噪声分量标准差，说明基于恒星日滤波原理的误差修正方法所受干扰较多，存在较大误差，也证明了基于改进CEEMDAN算法分离多路径误差的可靠性．

表2 CEEMDAN分解后IMF分量有效系数

Tab.2 Effective coefficients of the IMFs after CEEMDAN decomposition

表3 3天位移序列标准差

Tab.3 STD values of the three-day displacement series

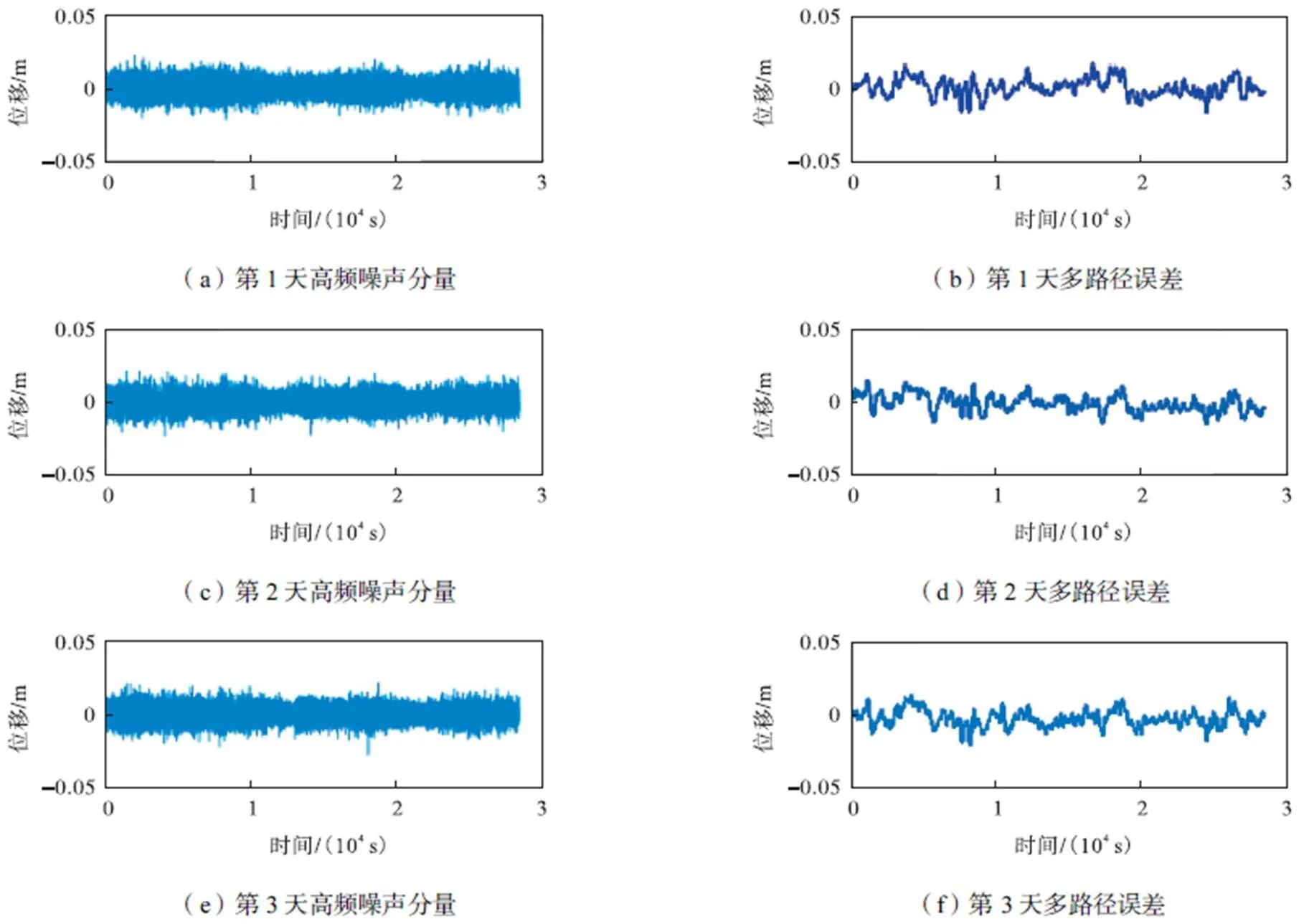
图4 改进CEEMDAN分解后位移序列

4 多种环境下GNSS-RTK稳定性试验

基于RTK实时动态差分技术，可直接获取点位的三维坐标序列．理论上监测值应固定不变，但由于多路径误差和仪器内部观测噪声影响，导致监测点坐标随时间变化．在设备调制和差分方式统一的前提下，变化的差异主要来自不同环境下的多路径效应．

选择开阔的平坦地面和水面两种较常见的环境进行GNSS-RTK定点观测试验，如图5所示．基准站布置在开阔平坦地带，移动站布置在距离基准站小于1km的范围内，满足信号接收要求．卫星高度截止角为15°，信号采样频率为5Hz，持续时间2h．

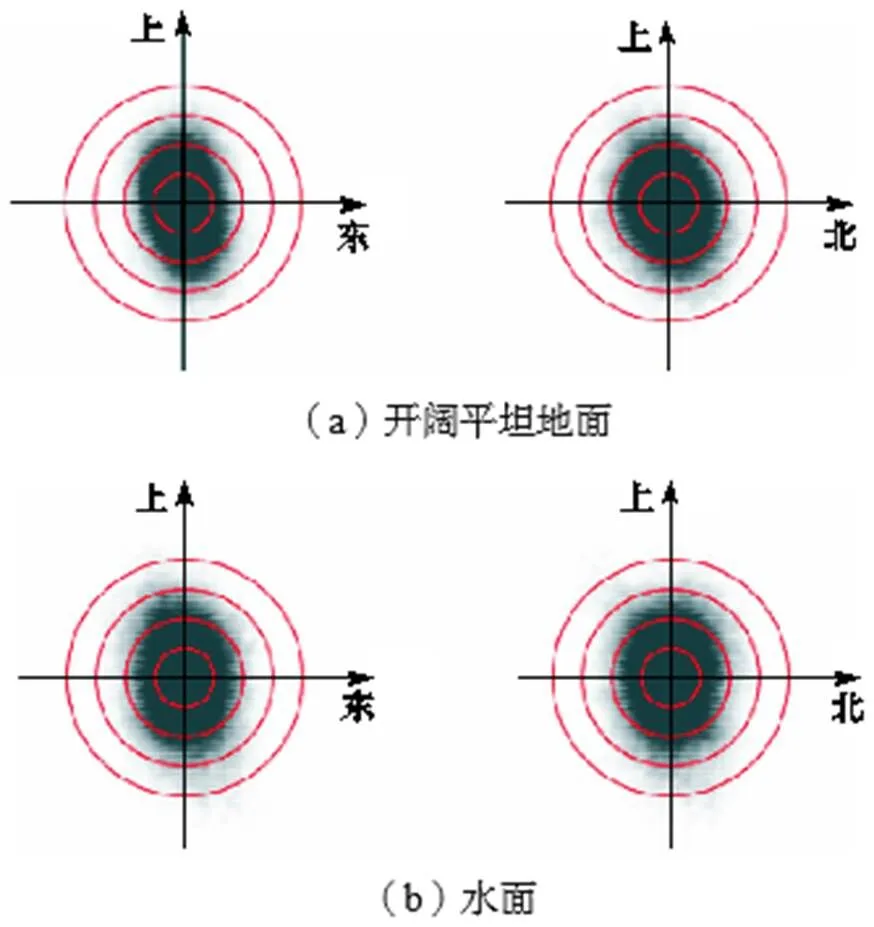
图6为两种环境下GNSS-RTK监测得到的定位点云．可以看出：在水平方向，开阔的平坦地面环境下得到的点云图离散程度最小，开阔水面环境次之，两者的点云大都分布在半径10mm范围内．在高程方向，平坦地面的点云图离散程度较小，两种环境下的点云大都分布在半径20mm范围内．总体来看，在水域环境下，GNSS-RTK监测多路径误差较大．高程方向点云的离散程度均大于水平方向，这是GNSS监测系统本身特性决定的．

图5 GNSS-RTK定点观测试验

截取高程方向、时长为2000s的监测数据进行分析．经过改进CEEMDAN算法处理后，两种监测环境下的原始信号序列、噪声序列、多路径误差序列和频谱分布如图7和图8所示．可以看出，两种环境下的高频噪声序列幅值相差不大，主要分布在±0.02m区间内．对于多路径误差序列幅值：开阔平坦地面环境下的位移分布在-0.015～0.005m范围内，幅值为0.020m；水域环境为-0.010～0.015m，幅值为0.025m．多路径误差序列的频域分布为地面(0.05Hz)＜水面(0.10Hz)．因此，采用GNSS进行桥梁、高层等结构变形监测时，应当尽量避免水面等强反射物的影响．同时，在进行信号滤波降噪处理时，可综合考虑结构自振频率及现场监测环境的影响，合理确定带通滤波频率．

注：同心圆半径从内向外依次为0.005m、0.010m、0.015m和0.020m

图7 开阔平坦地面环境下高程方向监测信号

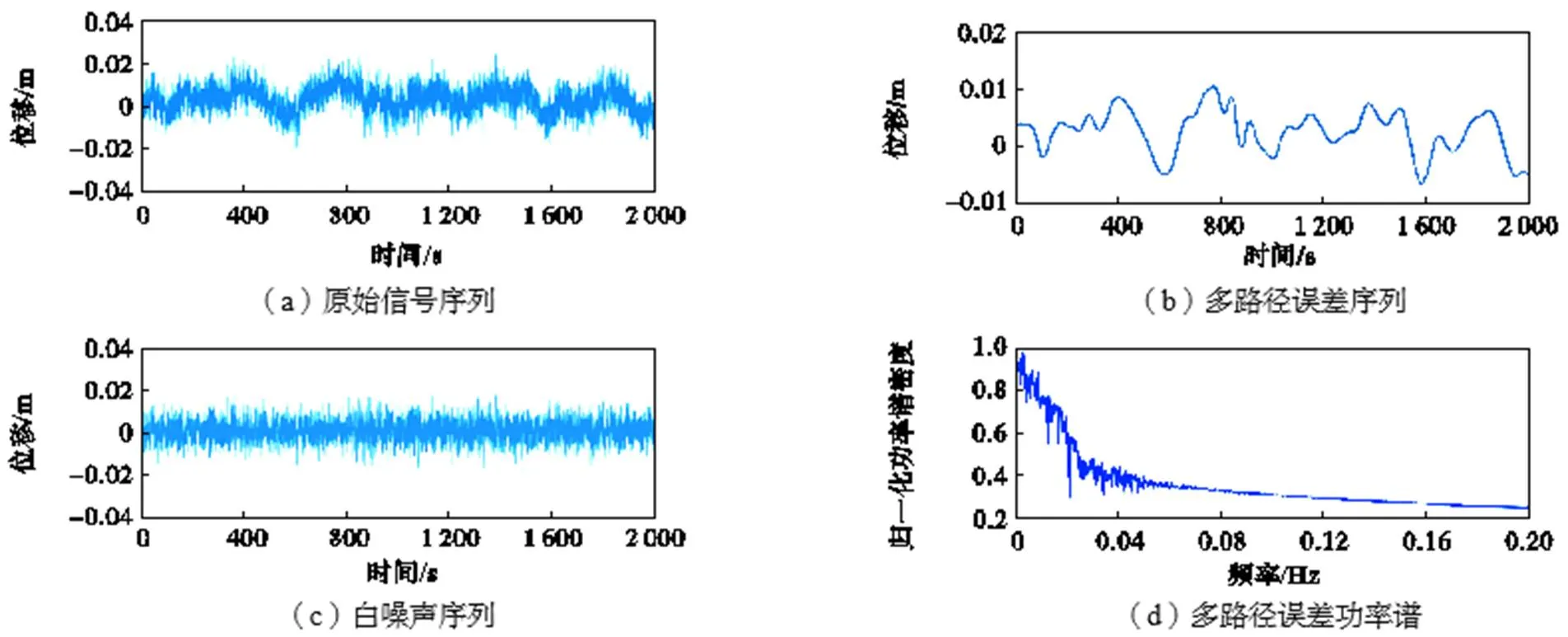
图8 水域环境下高程方向监测信号

5 GNSS-RTK桥梁监测试验

天津海河大桥由结构构造相同、建造时间不一的新老两座大桥组成，每座大桥承载单向交通．主桥为非对称单塔斜拉桥，桥面宽23m，塔高167.3m，跨径布置为46m＋48m×3＋310m．经过有限元模拟，桥梁前3阶自振频率分别为0.360Hz、0.616Hz和0.875Hz；主跨距离主塔225.2m处，桥面竖向挠度最大，为桥梁的最不利截面．本次试验以老桥的主桥为对象，在最不利截面处布置GNSS-RTK和拾振器进行联合监测．GNSS-RTK接收机架设在维修栈道内，拾振器放置在栈道护栏上，与移动站并列排放，如图9所示．拾振器采用速度型采集模式，拾振器和GNSS-RTK采样频率均为50Hz，持续采样3h．

图9 GNSS-RTK联合拾振器监测桥梁试验

截取时长为1000s的竖向振动信号进行分析．经过CEEMDAN分解，得到16个IMF分量，各IMF分量的相关系数和有效系数如表4所示. IMF1～IMF5有效系数均小于3，符合高斯白噪声特性，判定为仪器内部随机噪声．对IMF6～IMF15进行重构，重构信号与原始信号的振动位移时程曲线如图10所示．可以看出，经过改进CEEMDAN分解重构后，信号的毛刺问题明显改善，说明高频随机噪声得到有效抑制．

表4 桥梁监测信号IMF分量相关系数及有效系数

Tab.4 Effective coefficients and correlation coefficients of the monitored signal’s IMFs

图10 海河大桥竖向振动位移时程曲线

由监测试验得出水域环境下的多路径误差频率主要分布在0.1Hz范围内，而经有限元模拟得出的桥梁竖向振动基频为0.360Hz．设计通带频率为0.3Hz的巴特沃斯高通滤波器，对重构信号做进一步处理，以消除低频多路径误差干扰．另一方面，对拾振器监测得到的速度信号进行积分处理并去除漂移误差．拾振器与滤波前后RTK的竖向振动位移时程曲线如图11所示，经改进CEEMDAN与巴特沃斯联合滤波后，RTK信号幅值明显减小．以均方根误差为评价指标，分析了应用联合算法滤波降噪的效果．RTK位移时程序列的均方根误差值如下：原始序列(0.0148)＞CEEMDAN重构序列(0.0142)＞CEEMDAN-Butterworth联合滤波序列(0.0072)．经过联合滤波降噪处理后，RTK序列的均方根误差值大大减小，说明多路径误差得到有效抑制．此外，联合滤波降噪后的RTK振动位移时程曲线趋势与拾振器结果基本一致，说明两种传感器监测结果频域特征一致，反映了RTK监测的可靠性．

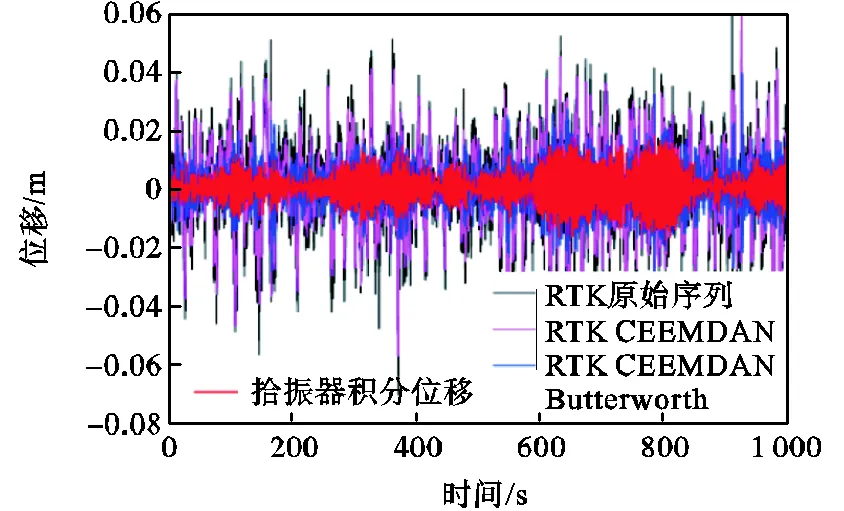
图11 拾振器与滤波前后RTK竖向振动位移时程曲线

6 结 论

(1) 采用CEEMDAN算法对加噪的仿真信号进行滤波降噪处理，基于有效系数阈值的判定结果与基于相关系数的判定结果一致，证明改进CEEMDAN算法能够有效分离高频白噪声．

(2) 基于连续多天定点观测试验，采用改进CEEMDAN算法提取的每日多路径误差序列优于恒星日滤波结果，说明改进CEEMDAN算法能够提取GNSS-RTK多路径误差．

(3) 通过开阔的平坦地面和水面两种环境下的GNSS-RTK稳定性试验，得出水域环境下多路径误差较大，多路径误差序列频域分布如下：地面(0.05Hz)＜水面(0.10Hz)．因此，在已知多路径效应和结构振动基频且结构基频远小于多路径误差频域的情况下，可直接采用高通滤波器滤除多路径误差．

(4) 联合改进CEEMDAN算法和巴特沃斯高通滤波器对GNSS-RTK桥梁实测信号进行滤波降噪处理，成功提取了海河大桥的动态位移，结果与拾振器监测结果基本一致，证实了GNSS-RTK监测桥梁动态变形和改进CEEMDAN算法进行滤波降噪的可行性．本研究可为基于GNSS-RTK技术的结构变形监测及噪声削弱提供参考．

［1］ 李宏男，伊廷华，王国新. GPS在结构健康监测中的研究与应用进展[J]. 自然灾害学报，2004(6)：124-132.

Li Hongna，Yi Tinghua，Wang Guoxin. Advance in research and application of GPS to structural health monitoring[J]. Journal of Natural Disasters，2004(6)：124-132(in Chinese).

［2］ 钟 萍，丁晓利，郑大伟，等. Vondrak滤波法用于结构振动与GPS多路径信号的分离[J]. 中南大学学报：自然科学版，2006，37(6)：181-187.

Zhong Ping，Ding Xiaoli，Zheng Dawei，et al. Separation of structural vibrations and GPS multipath signals using Vondrak filter[J]. Journal of Central South University：Science and Technology，2006，37(6)：181-187(in Chinese).

［3］ 伊廷华，张永恒，李宏男，等. 基于改进粒子滤波算法的GPS多路径效应理论与试验研究[J]. 应用基础与工程科学学报，2011，19(3)：429-440.

Yi Tinghua，Zhang Yongheng，Li Hongnan，et al. Theoretical and experimental investigations of GPS multipath effect based on improved particle filtering algorism[J]. Journal of Basic Science and Engineering，2011，19(3)：429-440(in Chinese).

［4］ 蒋光伟，程传录，王 斌，等. 影响GNSS数据质量的多路径效应相关性分析[J]. 地球物理学进展，2018，33(2)：461-466.

Jiang Guangwei，Cheng Chuanlu，Wang Bin，et al. Effection of data quality relativity analysis of multipath [J]. Progress in Geophysics，2018，33(2)：461-466(in Chinese).

［5］ 戴吾蛟，丁晓利，朱建军，等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报，2006，35(4)：27-33.

Dai Wujiao，Ding Xiaoli，Zhu Jianjun，et al. EMD filter method and its application in GPS multipath[J]. Acta Geodaetica et Cartographica Sinica，2006，35(4)：27-33(in Chinese).

［6］ 罗飞雪，戴吾蛟，唐成盼，等. 参考经验模态分解-独立分量分析及其在GPS多路径误差处理中的应用[J]. 测绘学报，2012，41(3)：54-59.

Luo Feixue，Dai Wujiao，Tang Chengpan，et al. EMD-ICA with reference signal method and its application in GPS multipath[J]. Acta Geodaetica et Cartographica Sinica，2012，41(3)：54-59(in Chinese).

［7］ 张昊楠，匡翠林，卢辰龙，等. 基于小波滤波和 PCA 组合的多路径改正方法[J]. 大地测量与地球动力学，2013，33(4)：137-141.

Zhang Haonan，Kuang Cuilin，Lu Chenlong，et al. A multipath correction method based on wavelet filtering and PCA[J]. Journal of Geodesy and Geodynamics，2013，33(4)：137-141(in Chinese).

［8］ 赵 龙，高井祥，李增科，等. 基于CEEMD-Wavelet-SavGol模型的GPS多路径修正算法[J]. 测绘通报，2017(11)：4-8.

Zhao Long，Gao Jingxiang，Li Zengke，et al. GPS multipath correction algorithm based on CEEMD-Wavelet-SavGol model[J]. Bulletin of Surveying and Mapping，2017(11)：4-8(in Chinese).

［9］ 敖敏思，胡友健，赵 斌，等. PCA和KLE在高采样率GPS定位中的应用[J]. 大地测量与地球动力学，2011，31(6)：145-150.

Ao Minsi，Hu Youjian，Zhao bin，et al. Application of PCA and KLE to high-rate positioning[J]. Journal of Geodesy and Geodynamics，2011，31(6)：145-150(in Chinese).

［10］ 韩厚增，王 坚，孟晓林. GPS与加速度计融合桥梁变形信息提取模型研究[J]. 中国矿业大学学报，2015，44(3)：549-556.

Han Houzeng，Wang Jian，Meng Xiaolin. Reconstruction of bridge dynamics using integrated GPS and accelerometer[J]. Journal of China University of Mining & Technology，2015，44(3)：549-556(in Chinese).

［11］ 伊廷华，张永恒，李宏男，等. 建筑材料特性对GPS监测信号影响规律的试验研究[J]. 振动与冲击，2011，30(10)：19-24，44.

Yi Tinghua，Zhang Yongheng，Li Hongnan，et al. Test for influence of common construction materials on GPS monitoring signals[J]. Journal of Vibration and Shock，2011，30(10)：19-24，44(in Chinese).

［12］ 朱 响. GNSS多路径效应与观测噪声削弱方法研究[D]. 西安：长安大学，2017.

Zhu Xiang. Research on GNSS Multipath Effect on Observed Noise Reduction Method[D]. Xi’an：Chang’an University，2017(in Chinese).

［13］ Niu Yanbo，Xiong Chunbao. Analysis of the dynamic characteristics of a suspension bridge based on RTK-GNSS measurement combining EEMD and a wavelet packet technique[J]. Measurement Science and Technology，2018，29(8)：085103.

［14］ 严 超，王 庆，杨高朝，等. EMD-RLS联合滤波算法及其在北斗多路径削弱误差中的应用[J]. 中国惯性技术学报，2019，27(2)：190-198.

Yan Chao，Wang Qing，Yang Gaochao，et al. EMD-RLS combination algorithm and its application in weakening BDS multipath error[J]. Journal of Chinese Inertial Technology，2019，27(2)：190-198(in Chinese).

［15］ 伊廷华，李宏男，伊晓东，等. 基于自适应噪声抵消与小波滤波的GPS监测误差分析[J]. 武汉大学学报：信息科学版，2006，31(11)：995-998.

Yi Tinghua，Li Hongnan，Yi Xiaodong，et al. On GPS observation errors with ANC principles and wavelet denoise method[J]. Geomatics and Information Science of Wuhan University，2006，31(11)：995-998(in Chinese).

［16］ Wang Jian，Wang Jinling，Roberts C. Reducing GPS carrier phase errors with EMD-wavelet for precise static positioning[J]. Survey Review，2009，41(312)：152-161.

［17］ Torres M E，Colominas M A，Schlotthauer G，et al. A complete ensemble empirical mode decomposition with adaptive noise[C]// Proceedings of the IEEE International Conference on Acoustics，Speech，and Signal Processing. Prague：IEEE，2011.

［18］ 王文哲，吴 华，王经商，等. 基于CEEMDAN的雷达信号脉内细微特征提取法[J]. 北京航空航天大学学报，2016，42(11)：2532-2539.

Wang Wenzhe，Wu Hua，Wang Jingshang，et al. Subtle intrapulse feature extraction based on CEEMDAN for radar signals[J]. Journal of Beijing University of Aeronautics and Astronautics，2016，42(11)：2532-2539(in Chinese).

［19］ 吴 军，黎国强，吴超勇，等. 数据驱动的滚动轴承性能衰退状态监测方法[J]. 上海交通大学学报：自然版，2018，52(5)：538-544.

Wu Jun，Li Guoqiang，Wu Chaoyong，et al. Data-driven performance degradation condition monitoring for rolling bearings[J]. Journal of Shanghai Jiaotong University：Science，2018，52(5)：538-544(in Chinese).

［20］ Huang Norden E，Shen Zheng，Long S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A，1998，454(1971)：903-995.

［21］ Wu Zhaohua，Huang Norden E. Ensemble empirical mode decomposition：A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis，2009，1(1)：1-41.

［22］ Yeh Jia Rong，Shieh Jian Shing，Huang Norden E. Comple mentary ensemble empirical mode decomposition：A novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis，2010，2(2)：135-156.

［23］ Flandrin P，Rilling G，Goncalves P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters，2004，11(2)：112-114.

［24］ 褚福磊，彭志科，冯志鹏. 机械故障诊断中的现代信号处理方法[M]. 北京：科学出版社，2009.

Chu Fulei，Peng Zhike，Feng Zhipeng. Modern Signal Processing Methods in Mechanical Fault Diagnosis[M]. Beijing：Science Press，2009(in Chinese).

A GNSS-RTK Monitoring Signal Processing Method Based on Improved CEEMDAN Decomposition

Yu Lina1，Xiong Chunbao1，Xiong Aicheng2，Zhu Jinsong1，Wang Meng1

(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin Luhai Surveying and Hydrography Co.，Ltd.，Tianjin 300191，China)

The monitoring accuracy of GNSS-RTK is affected by the multipath effect and white noise inside the instrument. Therefore，an improved CEEMDAN algorithm based on an effective coefficient to sift the IMF components is proposed to separate the signal and noise and improve the monitoring accuracy. First，the proposed algorithm was verified by signal simulation. Second，a consecutive and fixed-point monitoring experiment was conducted using GNSS-RTK to verify the reliability of the improved CEEMDAN in extracting the multipath errors. Next，GNSS-RTK stability tests were performed in an open flat ground and water area to analyze the multipath effect in different environments. Finally，taking Tianjin Haihe Bridge as an example，the GNSS-RTK monitored signal was filtered and the dynamic response of the bridge under environmental excitation was obtained. Results showed that the improved CEEMDAN algorithm can achieve a more accurate decomposition and reconstruction of the IMF components，thus effectively separating the high-frequency white noise components and low-frequency multipath errors. In the open flat ground and water area，the multipath effect exhibited a small influence. The frequency domain distribution of the multipath error sequence was as following：Ground(0.05Hz)＜water surface(0.10Hz). The frequency band for filtering was determined considering the natural structural frequency and monitoring environment，based on which the GNSS-RTK signal was filtered and the dynamic displacement of the Haihe Bridge was successfully extracted. The monitored results of GNSS-RTK were consistent with the results acquired from the vibration sensors.

improved CEEMDAN；GNSS-RTK；consecutive and fixed-point monitoring experiment；stability experiment；bridge dynamic deformation monitoring

P228.42

A

0493-2137(2021)08-0816-09

10.11784/tdxbz202009011

2020-09-04；

2020-11-20.

于丽娜（1991—  ），女，博士研究生，yulina@tju.edu.cn.

熊春宝，luhai_tj@126.com.

国家重点研发计划资助项目(2018YFB1600300).

Supported by the National Key Research and Development Program of China(No. 2018YFB1600300).

(责任编辑：金顺爱)